基于主从博弈的海上风电接入系统鲁棒规划

符 杨，刘智彬，刘璐洁，李传文，黄玲玲，耿福海

（1.上海电力大学电气工程学院,上海市 200090；2.国家电投集团上海能源科技发展有限公司,上海市 201101）

0 引言

海上风电是实现国家“双碳”战略目标的重要举措。2021 年,全球海上风电新增装机容量21.1 GW,其中中国的海上风电增量占全球的80%,成为全球海上风电累计装机容量最多的国家［1］。海上风电的大规模开发、集群化并网对接入的陆上电网扩展规划影响越来越大,大规模海上风电并网如何与陆上电网协调发展成为海上风电行业关注的热点之一。

相比于陆上风电并网,大规模海上风电接入系统规划具有以下特点:一方面,由于涉及海洋工程,海上风电并网项目建设运营成本高昂,为了引导海上风电的有序建设和可持续发展,其投资运营主体逐步由海上风电开发商单主体向电力传输系统运营商（electricity transmission system operator,ETSO）、海上独立输电运营商（offshore transmission owner,OFTO）等多主体形式转变［2］,大规模海上风电接入系统规划呈现多投资运营主体的特点,各主体的利益诉求不尽相同；另一方面,海上风电出力主要受海洋气象环境影响,由于其演化迅速,风电出力的不确定性更强,对海上风电接入系统规划所带来的影响也更为显著。如何将海上风电接入系统的投资运营主体利益诉求和不确定性影响结合充分考虑,是投资者们需要考虑的问题。

目前,在海上风电接入系统规划方面,主要考虑系统的经济性和可靠性建立单目标或多目标函数进行决策规划。文献［3-5］提出不同的海上输电网规划模型,同时考虑了陆上电网的扩展。文献［6］提出了一种海上输电网双层规划模型,上层确定合适类型的输电技术和网络拓扑,下层考虑各种不确定性因素,最终得到总成本最优的规划方案。上述文献都是基于整体理性的思想,对各主体利益诉求的考虑尚不充分。博弈是一种能够统筹兼顾每一主体利益诉求的方法,目前博弈思想在电力系统规划领域中应用广泛。文献［7-9］从博弈的角度对综合能源系统进行博弈规划,在充分考虑各个投资主体的利益诉求下得出最优的规划策略。综上所述,在海上风电接入系统规划当中,应用博弈方法的研究未见报道。

刻画源荷侧的不确定性方法主要有多场景法、随机规划法和鲁棒优化法［10］。文献［11］利用多场景法处理风电的不确定性,将不确定性描述加入含风电并网的输电网规划模型中。文献［12］利用随机规划法处理风电和负荷的不确定性,发展出引入私人投资的含风电并网的输电网规划模型。文献［13］利用鲁棒优化的方法处理风电出力的不确定性,构建了基于风电极限场景的两阶段输电网鲁棒规划模型。前两者依赖于实际工程中大量的历史数据或者难以求得的概率分布,且随着历史数据的增加,求解速率和结果都会受到影响。而鲁棒优化依赖于不确定集的建立,只需较少的数据信息就能描述随机变量的不确定性,相较于另外两种方法更具有鲁棒性。

结合上述研究现状及海上风电并网的特点,海上风电接入系统规划面临的问题主要包括:1）在海上风电接入系统投资运营模式多样化的趋势下,统筹规划多投资主体的海上及陆上输电网,并平衡不同投资方的利益是规划难点之一；2）准确刻画海上风电出力的波动性及相关性特征,提升接入系统规划的鲁棒性仍有待解决。

针对上述问题,本文提出基于主从博弈的海上风电接入系统鲁棒规划方法。首先,分析接入系统的投资运营模式及各投资主体间的利益冲突关系,构建海上风电接入系统主从博弈规划模型；然后,在此基础上考虑海上可及性受限下接入系统的运行维护方式,构建海上风电开发商规划模型。针对海上风电出力不确定性的问题,采用基于椭球不确定集鲁棒优化处理风电出力的随机性和相关性,构建电力传输系统运营商两阶段鲁棒规划模型。最后,结合粒子群算法和列与约束生成（C&CG）算法对整体模型进行求解。通过算例仿真对比验证了本文所提方法的有效性和合理性。

1 海上风电接入系统投资运营模式及博弈关系

1.1 投资运营模式

大规模海上风电接入系统的投资运营成本高昂,为了分摊其成本及运行风险,目前国内外发展了多种海上风电接入系统的投资运营模式,主要有发电商建设和ETSO 建设两种投资运营模式［14］,如图1 所示。

发电商建设模式,即以海岸线作为投资分界面,海上风电开发商（以下简称开发商）或OFTO 负责建设和运营海上输电网部分,包括海上升压站/换流站、陆上变电站/换流站、海缆、陆上电缆,ETSO 负责陆上电网扩建。ETSO 建设模式,即以海上风电场作为投资分界面,海上风电场内集电系统由开发商负责,场外海上输电网的建设和运营及陆上电网扩建由ETSO（以下简称运营商）负责。

1.2 投资运营主体的主从博弈关系分析

如何在多个投资主体参与下的接入系统规划中兼顾多主体间的利益,已逐渐成为海上风电有序建设和可持续发展的一个重要问题。为此,本文对有多个投资主体参与的发电商建设模式下的接入系统规划进行建模。大规模海上风电接入陆上电网,开发商与运营商的利益诉求各异。在规划过程中,开发商从自身利益出发,以降低海上输电网的投资运营成本、增加收益为目标,决策海上输电网方案,会影响运营商的扩建决策和收益；运营商以降低陆上电网的投资运营成本、增加收益为目标,决策陆上电网扩建方案,会影响开发商的决策和收益,两者独立决策但相互影响,双方形成非合作博弈的关系。

根据《关于促进非水可再生能源发电健康发展的若干意见》［15］可知,2022 年后新增的海上风电不再纳入中央财政补贴范围,由地方按照实际情况予以支持。在海上风电上网平价时代,短时间内海上风电接入系统投资运营成本难以通过上网电价疏导,开发商面临如何有效解决海上风电接入系统投资运营成本过高和将发的风电尽可能消纳的突出问题。

海上输电网和陆上电网协调规划,可以合理疏导海上风电接入系统投资运营成本,陆上电网能够进一步消纳风电。在发电商建设模式下,接入系统中的海上/陆上电缆、海上/陆上变电站（换流站）等大部分输电设备由开发商投资决策,在整个规划中起着主导地位,运营商在开发商决策后,优化扩建方案,两者之间形成以开发商为领导者,运营商为跟随者的主从博弈关系。

由于需要在各个主体独立决策自身方案的前提下共同完成整个海上输电网-陆上电网扩建规划,双方在规划过程中会掌握对方的所有策略信息。从开发商的角度,考虑海上可及性和维护方式影响,构建以净现值最大化为目标的规划模型；从运营商的角度,采用鲁棒优化方法处理风电出力的随机性和相关性以及负荷需求的不确定性,构建两阶段鲁棒规划模型,如图2 所示。

图2 主从博弈关系图Fig.2 Stackelberg game relationship chart

根据上述主从博弈关系,由博弈三要素（博弈参与者、博弈策略和收益函数）［16］构成主从博弈模型,简记为博弈元素如下:

1）博弈参与者N:开发商和运营商；

2）博弈策略集合Si={X,Y},x∈X,y∈Y；其中,X和Y分别为开发商和运营商的博弈策略集合,x和y分别为开发商和运营商的博弈策略集合中的一个策略方案；

3）收益函数Pi={P1,P2},P1=PNPVE(x,y),P2=PNPVG(x,y),其中,PNPVE为开发商全生命周期内的净现值,PNPVG为运营商全生命周期内的净现值。

(x∗,y∗)是Γ的一对纳什均衡解,即均衡状态下的开发商和运营商的规划策略。在均衡状态下,任何参与者单方面改变其策略都无法获得更大的利益,即

2 各投资运营主体的规划模型

2.1 开发商规划模型

本文以海上输电网全生命周期内的净现值PNPVE为目标函数,其收入为年售电（卖给运营商）收入IWG,t,成本包括海上风电场建设成本CP、海上输电网建设成本CCOFG以及年运维成本Cwm,t。决策变量为输电技术、线路的额定电压等级和横截面积以及公共连接点（PCC）的选择和并网容量等。

2.1.1 开发商目标函数

式中:Vt为在运营年t开发商的净现金流,属于将来值；r为资金折现率；T为全生命周期年数；Ω为变电站、换流站以及PCC 的候选集；ψ为输电线路的额定电压等级和横截面积候选集；x为0-1 变量,当x=1时,表示选取该候选方案,x=0 时,表示不选取该候选方案。

1）年售电收入IWG,t如式（6）所示。

2）海上输电网建设成本CCOFG包括海缆、陆上电缆、陆上变电站、海上升压站、换流站的建设成本。

式中:CCOFG,Line、CCOFG,S/CS分别为输电线路、变电站以及换流站的成本；ϕACvi表示是否选择交流海缆vi的0-1 变量；ϕDCfg表示是否选择直流海缆fg的0-1 变量；ϕAC、ϕDC分别表示是否选择高压交流传输和高压直流传输的0-1 变量,具体成本测算参考文献［17］；xvi,u、xvv,u分别表示是否选择电压等级u下交流海缆vi、vv的0-1 变量；Cac,linevi,u、Ccuvi分别为电压等级u下交流海缆vi的建设成本、无功补偿成本；Cdc,linefg,e、xfg,e分别表示电压等级e下直流海缆fg的建设成本和是否选择该类电缆的0-1 变量；Coh,lineim,h、Coh,linegm,h和xim,h、xgm,h分别表示电压等级h下陆上电缆im、gm的建设成本和是否选择该类电缆的0-1 变量；Clineff,e、xff,e分别表示电压等级e下直流海缆ff的建设成本和是否选择该类电缆的0-1 变量；xw,s表示是否选择海上升压站w和陆上变电站s的0-1 变量；xb,p表示是否选择海上换流站/海上交流平台b和陆上换流站p的0-1 变量；COFF,Sw/CAC,Platformw、CON,Ss、COFF,CSb/CDC,Platformb、CON,CSp分别为海上升压站/海上交流平台w、陆上变电站s、海上换流站/海上交流平台b、陆上换流站p的成本,主要取决于其额定容量的大小［17］；lvi、lvv、lfg、lff为海上待选输电走廊的线路回数；Clinevv,u、Clineff,e为连接站与站 的 海 缆 成 本；ψ∈{ψac,line,ψdc,line,ψoh,line},ψac,line、ψdc,line、ψoh,line分别为交流海缆、直流海缆、陆上电缆的电 压 等 级 和 横 截 面 积 候 选 集 合 ；Ω∈{ΩOFS,ΩONS,ΩOFCS,ΩONCS,Ωpcc},ΩOFS、ΩONS、ΩOFCS、ΩONCS、Ωpcc分别为海上升压站、陆上变电站、海上/陆上换流站及陆上并网点候选集合。

3）年运维成本Cwm,t。考虑海上可及性受限下海上风电接入系统的运维方式,本文采用事后维护和预防性维护相结合的维护策略［2］构建运维成本模型。

式中:C1、C2,t分别为每年的预防性维护成本和事后维护成本；γ为预防性维护成本占海上输电网总投资成本的比例［18］；{a}为海上输电网的元件（交直流海缆、变电站、换流站等）组成的集合；Cfailure,a为元件a的每次故障维护成本（包括运输故障部件相关的费用、执行维修/更换操作的维修技术人员费用以及风电场维修所需的所有消耗品和备件费用）,数据以及计算公式可参见文献为在运营年t元件a的平均故障次数；fa,t、ra,t分别为在运营年t元 件a的 故 障 率 和 修 复 率［17］；Cdowntime,a为 元 件a的每天停机损失为运营年t元件a的平均停机天数为发生在t=0 时元件a的故障平均修复时间［21］表示向上取整运算。

2.1.2 安全约束条件

1）决策变量约束

对于具有多个候选电压等级和横截面积的输电线路,只能同时选择一个,即

式中:PAC,CS,k为换流站k的输出功率；PDC,CS,k为通过换流站k的功率；PLOSS,CS,k为换流站k的功率损耗；PCS,N,k为换流站k的额定功率,其可选额定容量集合为ρOFCS∪ρONCS,其中ρONCS为陆上换流站的额定容量集合。

2.2 运营商两阶段鲁棒规划模型

考虑系统中源荷侧不确定性对接入系统规划的影响,本文计及风电出力的相关性,构建风电出力的不确定性集合,采用两阶段鲁棒优化对陆上电网规划进行建模,如式（25）所示。外层max 表示第1 阶段优化的问题,即寻找使目标函数最大的陆上电网扩建方案；中内层min-max 表示第2 阶段优化的问题,即中层min 在给定的线路规划方案下寻找风电出力和负荷需求不确定集中最恶劣的场景,内层max 在扩建方案和最恶劣的场景给定下通过调整运行变量（各发电机组出力）使规划方案满足所有的约束条件,并且使目标函数最大化。风电出力和负荷需求不确定集的构建见2.2.3 节。

本文以陆上电网全生命周期内的净现值PNPVG为目标函数。收入为年售电（卖给用户）收入IS,t；成本包括陆上电网新建成本CCONG、年购电成本CG,t、陆上电网新建线路年维护成本CMCONG,t、年弃风成本CWC,t。决策变量为陆上电网新建方案。

2.2.1 运营商目标函数

式中:o为陆上电网中的某条待选输电线路走廊；Ωon,line为陆上电网新建输电线路的待选集合；yo为待选输电走廊o的0-1 变量,yo=1 时,代表选取该条线路,yo=0 时,代表不选取该条线路；Ut为在运营年t运营商的净现金流；un为n时刻负荷不确定值；U为负荷不确定集合；Φ为海上风电出力的不确定集合；PG,i,n为原有电源中发电机组i在n时刻的输出功率；PWG,n为n时刻海上风电出力不确定值。

1）年售电收入IS,t

式中:Pg→ct为在运营年t运营商的年平均电价；Qa,t为在运营年t向原有电源商的购电量；Qe,t为在运营年t向开发商的购电量；Qloadt为在运营年t运营商的售电量；Ωl为陆上电网的总线路集合；Qloss,lt为在运

式中:PG,i和PmaxG,i、PminG,i分别为原有电源中发电机组i的出力及其上、下限值；Gi为原有电源中的发电机组集合。

2.2.3 不确定集的构建

对于负荷增长的不确定性,采用盒式不确定集合建模。对于海上风电出力的不确定性,由于海上风电集群开发的特点,风电出力的相关性更强,传统盒式不确定集难以描述其相关性,故引入椭球不确定集。该集合的构建通过计及每个变量的不同方差和变量间的协方差,在刻画出力不确定性的同时兼顾变量间的相关性,降低了保守性。

对于海上风电出力不确定性集合,根据海上风电历史出力场景的分布情况,利用数据驱动方法,采用最小体积闭包椭球（MVEE）算法［22］构建能够包裹所有历史出力场景的最小体积椭球不确定集合Φ,具体模型如下:

2.3 主从博弈均衡解的存在性证明

由主从博弈均衡解存在定理可知［23］:设领导者策略集合X是M维欧氏空间RM上的非空紧凸集,跟随者策略集合Y是RK上的非空紧凸集。领导者收益函数F:X×Y→R 上半连续,跟随者收益函数G:X×Y→R 上半连续。且∀x∈X,∀y∈Y,F(x,y)和G(x,y)为拟凹函数时,该主从博弈存在均衡解且唯一。

对于本文的主从博弈模型,开发商和运营商策略均为新建线路,其线路回数受输电走廊约束,即开发商和运营商的策略空间均为欧氏空间上的一个非空紧凸集。

定理1:设I是RK上的有界闭集,若集值映射是闭的,则F′在X上必是上半连续的。由开发商的净现值PNPVE表达式可知,博弈决策变量为海上输电线路路由,其输电线路回数受输电走廊约束,即PNPVE为海上新建输电线路的闭映射,证明PNPVE是上半连续的。同理,可证运营商的净现值PNPVG也为陆上扩建输电线路的闭映射,是上半连续的。

根据实际情况,总的新建线路回数在输电走廊约束中增加,收益先会上升,然后达到极大,最后下降。造成这样的原因是风力发电和原有发电机组的装机容量已经固定,刚开始收益会随着线路回数的增加而增加,此时收入的增加速度远大于成本的增加速度；当系统输电线路的传输容量满足全网电源的装机容量时,达到极大值；而后,当线路回数继续增加,由于装机容量一定,故此时收入大致不变,而成本继续增加,收益开始下 降 。各 个 策 略 方 案 满 足 ∀x1,x2∈R3,∀y1,y2∈R,∀λ∈(0,1),有PNPVE(λx1+(1-λ)x2)≥min {PNPVE(x1),PNPVE(x2)} 和PNPVG(λy1+(1-λ)y2)≥min {PNPVG(y1),PNPVG(y2)},证 明 了PNPVE和PNPVG为拟凹函数。综上所述,本文构建的海上风电接入系统主从博弈规划模型存在均衡解且唯一。

3 模型求解

本文提出的基于主从博弈的海上风电接入系统鲁棒规划模型属于双层规划模型,目标函数和约束条件都是线性的,模型中有连续变量和整数变量,属于混合整数线性规划模型,且模型中嵌套两阶段鲁棒优化问题,很难通过统一的优化方法进行求解,处理这类优化问题通常使用多个算法相结合进行求解［9］。因此,本文采用粒子群算法和C&CG 算法相结合进行模型求解。

上层开发商规划模型中决策变量的维度是高维的且求解规模较大,本文采用粒子群算法降低模型求解难度,相较于其他智能算法,粒子群算法具有求解效率高、迭代收敛快等优点［24］。下层运营商两阶段鲁棒规划模型,采用C&CG 算法求解,相较于Benders 分解算法具有求解速度快、迭代次数少等优点,具体求解流程见附录A。在MATLAB 中编写上述程序,并调用Cplex 求解器和Matpower 潮流计算包。将C&CG 算法嵌入粒子群算法迭代过程中,根据开发商传递过来的PCC 选址定容方案（简称并网方案）求解自身问题,并将求解得到的陆上电网输电线路扩建方案（简称扩建方案）反馈给开发商。

本文所提出的规划模型具体求解流程如图3 所示,求解步骤如下:

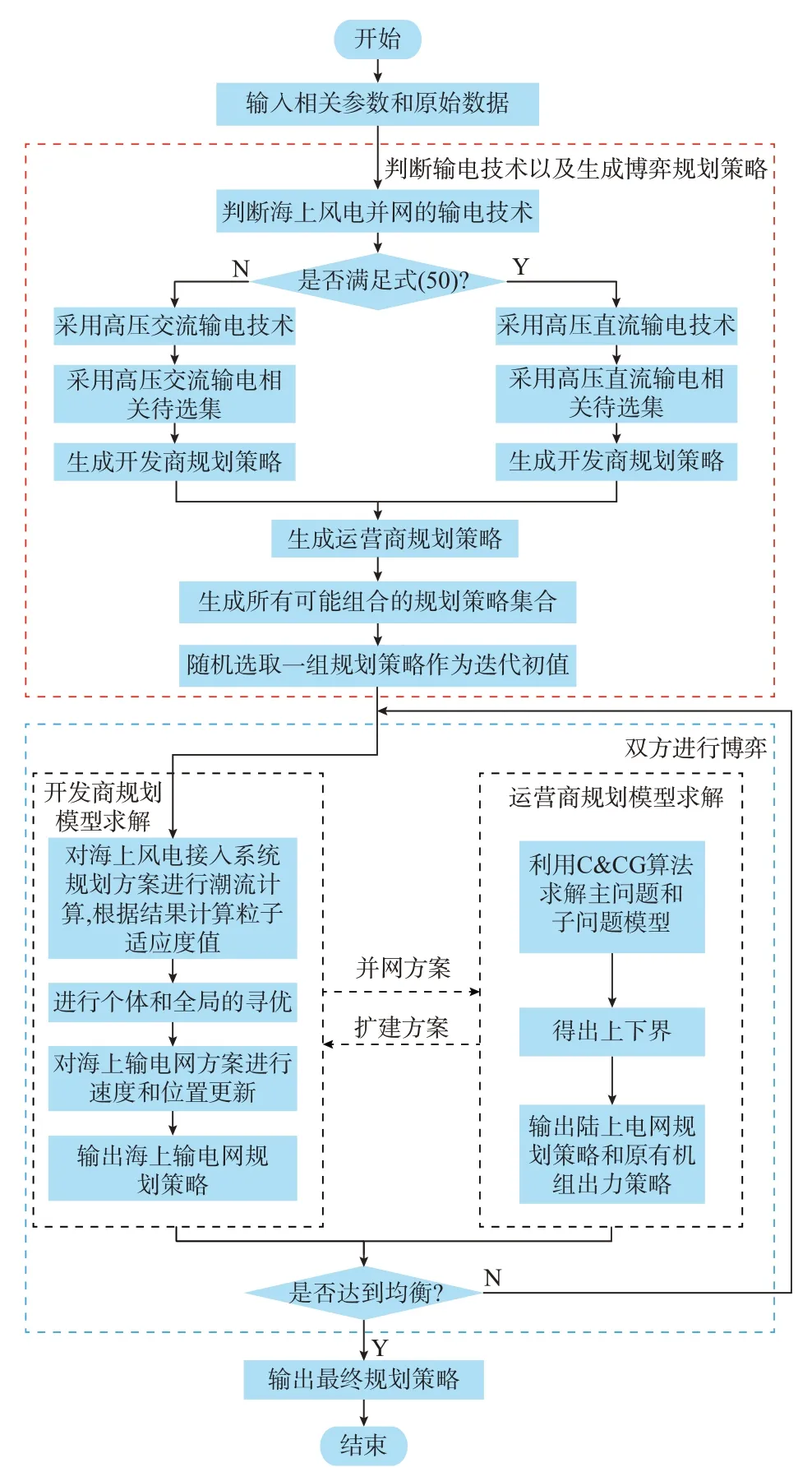
图3 求解流程图Fig.3 Flow chart of solving the proposed planning model

步骤1:输入风电场相关数据、陆上电网相关数据以及规划模型中相关已知数据和成本参数。

步骤2:判断线路的输电技术。计算高压直流输电技术的盈亏平衡距离lDC,如式（49）所示,然后与离岸距离loffshore比较,若结果如式（50）所示,则采用高压直流输电技术,反之则采用高压交流输电技术。PD为某条海缆D的假定潮流,以海上风电场的额定装机容量确定,具体公式如下［3］:

步骤4:根据步骤3 的规划策略,生成所有可能组合的规划策略集合。

步骤5:设定迭代初值。从步骤4 中随机选取一组规划策略作为求解算法的迭代初值。

步骤6:求解开发商规划模型。首先,根据初始规划方案进行潮流计算,并将潮流计算的结果（如支路潮流、节点电压等）代入开发商规划模型中,得到粒子的适应度值；其次,进行个体和全局的寻优,更新粒子的速度和位置,即对海上输电网规划方案进行更新；最后,将迭代求解的结果（并网方案）输入步骤7 中。

步骤7:求解运营商两阶段鲁棒规划模型。在开发商传递过来的并网方案下利用C&CG 算法进行求解,并再次进行潮流计算,得到满足约束条件前提下的最优陆上电网扩建方案,将扩建方案反馈给开发商,即步骤6,进行下一轮的博弈优化。

步骤8:双方进行博弈。双方进行博弈优化,即重复步骤6 和7,直到博弈均衡。开发商根据上一轮博弈中运营商反馈的扩建方案来调整自身的规划策略,决策出新的并网方案之后运营商再根据开发商传递的并网方案决策出自身的扩建方案。如此循环,直到相邻两轮双方的迭代结果相等时,即

则视为博弈达到均衡状态,跳出循环,进入步骤9中；否则,返回步骤6 继续寻优迭代。

步骤9:输出最终规划策略。输出均衡解,并计算出双方各自最终的净现值。

4 算例分析

4.1 算例参数设置

本文算例采用修改后的IEEE 30 节点系统作为陆上电网,该系统设有47 条输电走廊,包括41 条现有输电走廊以及6 条新建输电走廊,每个走廊最多建设两回输电线路,如附录B 图B1 所示。负荷需求进行了相应的改变,以应对大规模的海上风电接入。设节点3、6、8、11 和12 作为候选的PCC,设有6 个候选陆上变电站/换流站。海上风电场群装机容量见附录B 表B1,总装机容量为1 564.2 MW。利用K-means 聚类算法对海上风电场集群聚类,将得到的聚类中心作为海上变电站的选址。线路的电压等级和横截面积候选集参数见文献［5,17］。取无功补偿设备成 本 为42.86 万元/Mvar［25］。折现率r取8%。全生命周期年数T取25 年［19］。

为了验证本文所提方法的有效性和优越性,对以下4 个场景进行仿真:

场景1:独立规划。不考虑投资运营模式,陆上与海上独立规划。

场景2:联合规划。考虑投资运营模式,在发电商建设模式下,陆上与海上整体利益最优为目标进行联合规划。

场景3:主从博弈规划。考虑投资运营模式,在发电商建设模式下,统筹考虑开发商与运营商的利益诉求。

场景4（本文方法）:考虑主从博弈和不确定性的规划。在场景3 基础上,考虑风电出力和负荷增长的不确定性对规划方案的影响。

4.2 算例仿真结果及验证分析

4.2.1 仿真结果

4 种场景下的规划结果见附录B 图B2 和图B3。图B2 为海上输电网优化结果,图B3 为陆上电网优化结果。在场景1,海上风电场群通过2 座132 kV陆上变电站、2 座陆上换流站接入3、8 和11 这3 个并网点,接入的额定容量分别为590、770、204.2 MW。在场景2,海上风电场群通过2 座132 kV 陆上变电站、2 座陆上换流站接入3、6、8 和12 这4 个并网点,接入的额定容量分别为60、620、150、734.2 MW。在场景3 和4,海上风电场群通过2 座陆上变电站（电压等级分别为132 kV 和220 kV）、2 座陆上换流站接入3、6 和12 这3 个并网点,接入的额定容量分别为60、971.2、533 MW。海上风电接入系统输电线路的电压等级和横截面积优化结果见附录B表B2。

附录B 图B4 展示了场景4 下开发商和运营商净现值的优化迭代过程,在博弈过程中,两者在第49 轮博弈后达到收敛,由图B4 可见本文方法具有较好的收敛效果。当达到博弈均衡时,如图B4 所示任何一方改变其策略都无法获得更多的收益,此时开发商和运营商的净现值分别为78.96、73.37 亿元。

4.2.2 不同场景的对比验证

图4 为4 种场景下海上风电接入系统全生命周期主要成本构成。通过场景1 和2 的对比,验证联合规划的优越性。从图4 可见,场景1 的总成本在4 种场景下最高,相比于场景1,场景2 由于整体联合规划,协调风电的接入容量和负荷需求,考虑了陆上输电线路堵塞以及陆上电网PCC 附近电网结构强弱的情况,总成本降低4.99%。

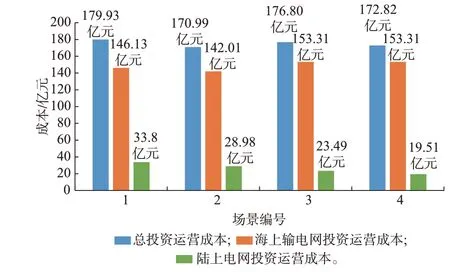
图4 4 种场景的全生命周期主要成本构成Fig.4 Main cost components for entire lifecycle of four scenarios

当存在利益冲突时,若以牺牲某一方的利益来使己方获得更大的利益,会导致资源配置不均衡。本文通过场景2 和3 的对比,验证存在不同投资主体利益冲突时,考虑博弈协调规划的优越性。从图4 可见,场景2 没有统筹兼顾两个投资主体各自不同的利益需求,虽然海上输电网投资运营成本有所降低,比场景3 低了7.37%,但陆上电网投资运营成本大幅度增加,比场景3 高了23.37%,以牺牲运营商的利益使得整体利益最大,降低了海上风电的投资活力,不利于海上风电的可持续发展。表1 为场景2、3、4 下两个投资主体的全生命周期净现值。

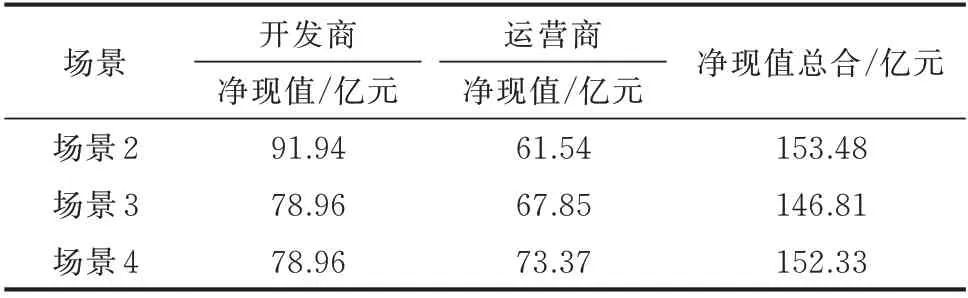
表1 场景2、3 和4 下两个投资主体的净现值Table 1 Net present value of two investment entities in scenarios 2, 3 and 4

由表1 可见,相比于场景2,场景3 中开发商的净现值降低了14.12%,运营商的净现值提高10.25%。采用基尼系数来衡量双方净现值之间的均衡程度［26］,基尼系数越小,越均衡,反之越不均衡。场景2、3 的基尼系数分别为0.216、0.095,场景3 的均衡性优于场景2。原因是场景3 统筹考虑了两个投资主体的利益,通过不断地博弈决策,优化出了均衡的决策组合方案。在海上风电接入系统投资运营模式多样化的趋势下,有益于提高海上风电投资建设的活力,也更加符合电力市场的实际运行机制。

本文通过场景3 和4 的对比,验证考虑风电出力和负荷不确定性因素对规划方案的影响。场景3 和4 的陆上电网扩建成本分别为9.61、12.82 亿元,弃风成本分别为9.81、0.95 亿元。虽然场景4 的陆上电网扩建成本比场景3 高了33.40%,但其全生命周期内的弃风成本大幅度降低,由表1 可见,最后净现值增加了8.14%,有效提高了规划方案应对不确定性影响的能力,并且具有良好的经济性。综上所述,通过不同场景的对比验证了本文所提方法的有效性和优越性。

4.2.3 不同鲁棒优化方法的经济性和鲁棒性对比

将本文的风电出力不确定集合构建方法（方法1）与基于盒式的风电出力不确定集合构建方法（方法2）进行对比,来验证本文方法的有效性和优越性。两种方法下开发商和运营商的投资运营成本对比如表2 所示。

表2 不同方法下两个投资主体投资运营成本的对比Table 2 Comparison of investment and operation costs of two investment entities with different methods

由表2 可见,相比方法2,方法1 开发商的投资运营成本降低了0.89%,运营商的投资运营成本降低了13.86%,原因是对于开发商而言,方法1 的不确定集比方法2 的不确定集保守性小,因此投资运营成本相应地降低了；对于运营商而言,由于方法1的不确定集保守性小,减少了陆上电网线路的投资成本,从而总体的投资运营成本有所降低。上述对比验证了基于本文构建的不确定集鲁棒规划模型的有效性和合理性。

采用4 320 组海上风电场群历史出力场景以及负荷需求验证规划方案的鲁棒性,风电场历史风速数据来源于ERA5 数据集,通过风电场出力-风速关系表达式转化为风电出力数据,假设负荷需求波动服从正态分布,从而随机生成4 320 组负荷数据集。基于蒙特卡洛模拟法的概率潮流计算方法对规划方案进行模拟运行,得出不同方法下运营商的最大总运行成本和平均总运行成本,具体结果见表3。风电出力（以案例中两个风电场群为例）以及负荷需求的不确定集见附录B 图B5 至图B7。

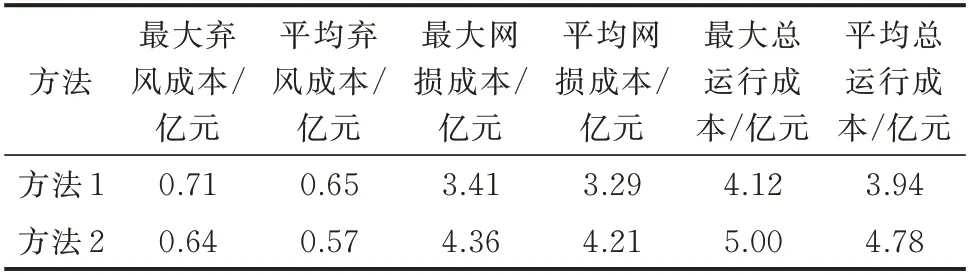
表3 不同方法的鲁棒性检验Table 3 Robustness check of different methods

对于海上风电出力的不确定性刻画,相比于盒式不确定集,椭球不确定集可以更好地包裹历史风电出力场景,且描述了风电场之间出力相关性,保守性降低,如附录B 图B5 和图B6 所示。而负荷的不确定性,用盒式不确定集来描述比椭球不确定集的保守性更小,如图B7 所示。平均运行成本主要反映规划方案的经济性指标,最大运行成本反映规划方案的鲁棒性指标［27］。由表3 可见,相比于方法2,方法1 中运营商的最大总运行成本降低了17.6%,说明本文所提方法可以提高规划方案的鲁棒性；平均总运行成本降低了17.57%,说明本文所提方法可以提高规划方案的经济性。

5 结语

结合海上风电接入系统投资运营模式多样化以及风电出力随机性和相关性的特征,提出一种基于主从博弈的海上风电接入系统鲁棒规划方法。具体结论如下:

1）通过算例仿真,本文方法相比于传统的独立规划,总体净现值增加了4.08%；相比于传统的联合规划,利益分配均衡程度明显提升,提升了127.37%。本文方法统筹兼顾了两者的利益,得出双方都满意的规划方案,有利于海上风电的可持续发展。

2）通过基于数据驱动的椭球不确定集鲁棒优化方法,处理风电出力的波动性和相关性以及负荷需求的不确定性,算例仿真表明考虑不确定性因素的影响能使运营商净现值增加8.14%。本文方法降低了保守性,提高了规划方案的经济性和鲁棒性。

本文是对海上风电接入系统进行中长期规划,后续可结合大规模海上风电场群的接入时序,在短期与中长期协同规划方面展开进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。