基于阻尼转矩分析的电力系统频率振荡模式辨别与分析

周 涛，孙 杰，徐 妍，任必兴，周一辰

（1.南京理工大学自动化学院,江苏省南京市 210094；2.江苏方天电力技术有限公司,江苏省南京市 211102；3.江苏省电力试验研究院有限公司,江苏省南京市 211103；4.华北电力大学电气与电子工程学院,河北省保定市 071003）

0 引言

随着中国推进以新能源为主体的新型电力系统建设,新能源占比的增加导致系统惯量减少,频率稳定性问题不容忽视［1-2］。近年来,在实际电网中观察到一些频率振荡现象,其振荡范围通常在0.01～0.10 Hz 内。土耳其、哥伦比亚电网均在高比例水电机组参与发电情况下,出现频率为0.05～0.08 Hz 的频率振荡现象［3-4］。而国内诸如藏中电网和云南电网均发生过0.05～0.11 Hz 之间的频率异常波动现象［5-8］。

频率振荡与传统低频振荡的形式有所不同,作为频率控制过程中出现的振荡模式,反映了全系统中原动机输出功率和负荷消耗功率之间的平衡过程［9-10］。低频振荡模式与发电机励磁环节相关,而频率振荡模式则与电力系统调频环节相关,两者不是同种模式,也不能轻易发生转变［11］。强迫功率振荡由系统中持续的周期性扰动引发,当扰动频率接近系统自然振荡频率时,会引起系统共振［12-14］。目前,在频率振荡过程中强迫振荡发生较少,其振荡引发机理有待研究。现针对频率振荡的研究大多围绕原动机调速系统的阻尼特性和调速系统参数对系统阻尼的影响展开［15］。文献［16］对频率振荡模式进行排查和分析,发现一对频率振荡特征根,其阻尼比与调速器参数密切相关。文献［17-18］研究了哥伦比亚电网和土耳其电网的频率振荡事件,前者频率振荡由调速系统前馈控制引起,而后者由调速器参数不合理引起。

频率振荡除与调速系统和水轮机的自身机械特性有关外,有学者指出系统自动发电控制（automatic generation control,AGC）也会导致频率振 荡 的 产 生［19］。一 次 调 频（primary frequency regulation,PFR）主要基于发电机的调速器和原动机,限制电网频率变化,而AGC 则是对控制区内各发电机组的有功出力重新进行调节分配［20-21］。文献［22］指出,系统中存在与一次调频强相关的PFR 模式和与AGC 强相关的AGC 模式。文献［23］结合中国云南电网实际运行状况,发现频率振荡与AGC 系统在调频死区内动作有关。文献［24］根据含AGC环节的开环传递函数奈奎斯特图和波特图,分析不同参数对于开环传递函数的影响。文献［25］基于Pade 近似方法研究延时对频率振荡模式的影响,以及对系统带来的阻尼恶化。目前,对于两种不同模式的表现和区别以及如何辨别两种振荡模式还有待进一步研究。

为了分析系统中不同调频过程对频率振荡的影响、厘清不同振荡模式的内在区别与振荡表现,本文将阻尼转矩分析（damping torque analysis,DTA）理论进行推广,提出电力系统频率振荡模式辨别方法,为电力系统频率振荡机理分析和抑制措施提供参考。本文的主要创新工作如下:

1）提出适用于电力系统频率稳定分析的DTA方法,建立适用于AGC 动态的电力系统频率振荡DTA 模型；

2）基于该模型分析频率振荡的影响机理,揭示在调频控制过程中阻尼转矩的分配和传递机理,明确不同调频环节向系统提供的阻尼转矩贡献；

3）定义模式辨别的DTA 指标,提出电力系统频率振荡模式辨别方法,分析不同模式之间的振荡表现和内在区别,并通过仿真分析验证本文方法的有效性和可行性。

1 电力系统频率振荡分析模型

频率振荡发生时,系统频率变化范围很小。因此,本文基于小干扰稳定分析方法,在稳态运行点附近对系统进行线性化建模,建立电力系统频率振荡的小干扰分析模型。

目前,电网中频率振荡事故大多发生在水电机组主导的系统中。在某一稳态工况点进行线性化,可以得到水轮机传递函数GW(s)为:

式中:ΔPm为机械功率偏差；ΔPv为调速器阀门变化量；TW为水锤效应时间常数。

火电机组的传递函数GCH(s)为:

式中:Δμch为汽门开度变化量；TCH为火电机组滞后时间常数。

发电机的传递函数可由机械功率、电磁功率及转速之间的关系得到,即

式中:Δf为频率偏差；ΔPe为电磁功率偏差；TJ为发电机转动惯量；Dl为阻尼系数。

仅考虑负荷的频率变化,则有

式中:ΔPl为负荷有功变化量；Kl为负荷调频效应系数。

负荷调频效应系数与发电机的阻尼系数作用相同。令D=Dl+Kl,得到发电机及负荷的传递函数Ggen(s)为:

一次调频的调速器传递函数Ggov(s)为:

式中:Tg为调速器响应时间常数；R为调差系数。

AGC 包含比例-积分（proportional-integral,PI）环节和延时环节,是一个非线性系统。区域控制偏差（area control error,ACE）计算方式为:

式中:ΔPtie为联络线功率偏差；VACE为ACE 值；β为频率偏差系数。

基于上述传递函数,建立包括原动机、发电机、调速器等在内的多区域频率振荡分析模型,如附录A 图A1 所示。图A1 所示的频率振荡分析系统中,单区域的动态特性由以下状态空间方程模型描述［26］:

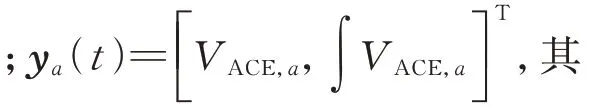
2 基于DTA 的频率振荡模式辨别

2.1 频率振荡DTA

DTA 的基本概念是稳定控制器向系统提供阻尼转矩,能够清晰揭示控制器阻尼转矩的产生、分配和传递的信息［27］。现有研究利用阻尼转矩法分析原动系统阻尼特性的适用性,为频率振荡中的应用提供基础。在第1 章建立的频率响应模型基础上,本节将构建和推导适用于频率振荡的DTA 方法,从而得出新场景下的分析结果和结论。

图1 所示为以分析AGC 控制环节为主的阻尼转矩传递示意图。图中:ΔPd为负荷信号；ΔTAGC为AGC 向发电机提供的阻尼转矩；ΔTPFR为PFR 向发电机提供的阻尼转矩；蓝色箭头线表示PFR 通过一次调频回路和原动系统向发电机提供阻尼转矩,再转化为对振荡模式阻尼的影响,以调差系数为反馈通道；红色箭头线表示AGC 通过AGC 控制环节和原动系统向发电机提供阻尼转矩,在多区域系统中以联络线和频率偏差系数为反馈通道。

图1 AGC 系统阻尼转矩传递示意图Fig.1 Schematic diagram of damping torque transmission of AGC system

对于AGC 调频环节,AGC 控制信号到发电机的传递函数FAGC(s)为:

假设系统中AGC 控制器的传递函数和反馈信号分别为GAGC(s)和Δyk,则有

以ΔPAGC为控制变量,将图1 所示的多区域电力系统的模型线性化表示为:

式中:C1、C2、C3、d为AGC 输出变量重构后的系数。

重构系数的具体计算方式见文献［27］,其依据具体系统中AGC 的连接方式。

由式（12）和式（16）可得重构函数为:

如果系统频率振荡与系统的第i个振荡模态相关联,则可以得到在复频率下AGC 向每一台发电机提供的阻尼转矩ΔTAGC为:

式中:λi为第i个模态；DAGC为AGC 向每台发电机提供阻尼转矩的系数。

式（18）表明,控制器并不是只向某一台发电机提供阻尼转矩,而是向每一台发电机都提供阻尼转矩。对于第i个振荡模态,控制器向第j台发电机提供的阻尼转矩Dij为:

式中:Fj为控制器到第j台发电机的传递函数；Gj为控制器传递函数；γj为控制器到第j台发电机的信号重构系数；Δfj为第j台发电机的频率偏差。

定义第i个模态λi对第i台发电机阻尼转矩的灵敏度指数Sij为:

式中:Δλi为第i个模态的变化量；ΔDij为第i个模态下对发电机阻尼转矩的变化量。

由式（19）可知,多区域系统中AGC 控制器向每台发电机都提供阻尼转矩。因此,发电机的阻尼特性就会受到影响,当AGC 控制器阻尼转矩发生改变时,模态变化的方程为:

式 中:DAGCj、FAGCj、γAGCj分 别 为AGC 到 第j台 发 电 机的阻尼系数、传递函数、信号重构系数；GAGCj为第j台发电机对应的AGC 的传递函数；N为发电机总数。

式（21）为AGC 向每台发电机提供阻尼转矩的通道,通过对每台发电机贡献的阻尼转矩再对振荡模态的阻尼产生影响。通过上述原理得到系统的阻尼转矩指标为:

式（22）表征了控制器对模态的影响能力,清晰表达了调频过程中AGC 控制器对模态提供阻尼的机理。

2.2 阻尼转矩指标及模式辨别

AGC 和PFR 模式不能根据振荡频率对频率振荡模式进行明确、科学的辨别,无法从理论上排除某些特殊参数下PFR 模式和AGC 模式振荡频率接近的可能［22-25］。文献［22］根据不同的参与因素定义了AGC 功率调节比来辨别不同模式,如附录A 式（A1）所示。

当系统调频过程中同时存在AGC 和PFR 动态作用时,两者会共同影响系统的调频性能和稳定性。本文基于2.1 节推导的DTA 模型,根据不同环节对振荡模态提供阻尼转矩的不同,提出新的模式辨别方法。

图2 展示了不同调频环节向发电机提供阻尼转矩,进而通过每台发电机的阻尼转矩贡献转化为对振荡模式阻尼的影响。通过对比两个调频向发电机提供的阻尼转矩大小,可以辨别系统频率振荡模式。图中:DPFR为PFR 向发电机提供阻尼转矩的系数。

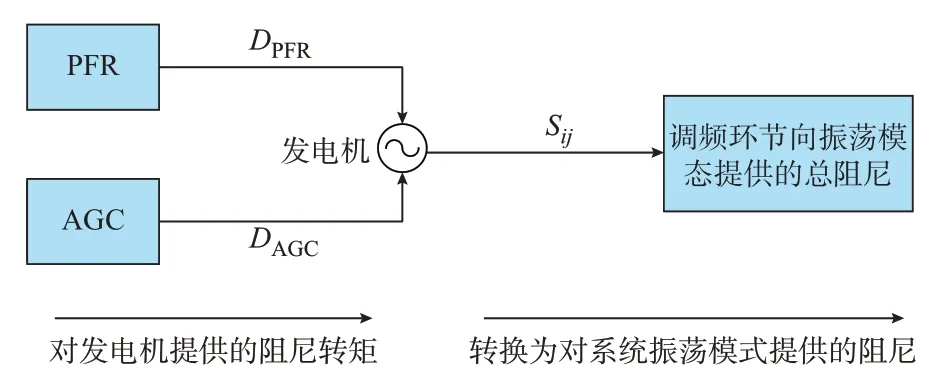
图2 调频环节影响频率振荡模式阻尼示意图Fig.2 Schematic diagram of influence of frequency regulation link on frequency oscillation mode damping

如果系统频率振荡与第i个振荡模态相关联,可以得到在复频率下AGC 向每台发电机提供的阻尼转矩ΔTAGC为:

式中:τ为延时参数。

同理,可以得到在复频率下PFR 环节向每台发电机提供的阻尼转矩ΔTPFR为:

如果Ddamp,PFRDdamp,AGC,则表明PFR 提供的阻尼转矩较大,为PFR振荡模式。该方法与已有的模式辨别方法相比,无须根据专家经验设定范围,辨别较为清晰、简便。

3 算例与分析

式中:FPFR为PFR 控制信号到发电机的传递函数；GPFR为PFR 环节的传递函数；γPFR为PFR 环节信号重构系数。

ΔTPFR的推导原理与AGC 环节相似,信号重构部分需要考虑联络线功率偏差以及AGC 延时环节。本文根据上述过程定义模式辨别指标Ddamp,n为:

式中:n取PFR、AGC,分别表示PFR 环节和AGC环节。

在MATLAB-R2020b/Simulink 中搭建单区域及多区域AGC 系统频率振荡分析模型。建立模型时以水电机组为主,结合原动机特性、AGC 控制器特性等因素。本文中具有实际物理意义的参数设置参考文献［22-26］,均在正常范围内。

3.1 方法验证与机理分析

本节首先以单区域系统为例,结合时域仿真分析测试,分析不同振荡模式的表现与区别。单区域系统模型为附录A 图A1 中任一区域,具体系统参数见附录A 表A1。

为了测试本文模式辨别指标的有效性和准确性,实验中构建临界情况下指标差值较小的场景,得到频率振荡曲线。对振荡曲线进行Prony 分析,得到系统振荡主导模式的幅值为8.347 1×10-5Hz,相位为1.459 2 rad,频率为0.142 8 Hz,阻尼比为0.897 2。

对系统进行特征值分析,如表1 所示,得到4 个实特征值和2 对共轭复特征值,即2 个振荡模式。振荡模式如表2 所示,可以得出振荡模式1 为该情况下系统频率振荡主导模式。

表1 PFR 振荡模式Table 1 PFR oscillation mode

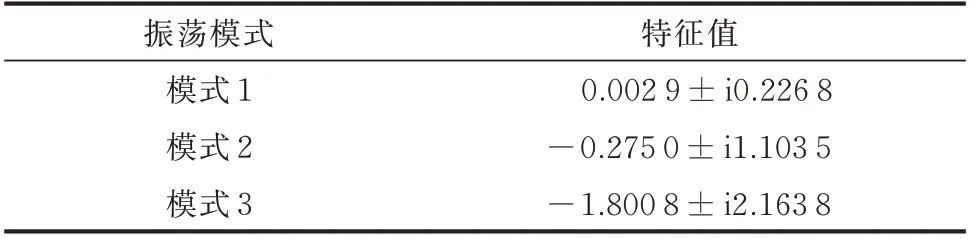
表2 AGC 振荡模式Table 2 AGC oscillation mode

模式辨别指标计算结果为Ddamp,PFR=18.681 0和Ddamp,AGC=18.073 4,得到Ddamp,PFR>Ddamp,AGC,可以判断此时的振荡模式为PFR 振荡模式。该场景下的两个指标结果差值较小,由于本文提出的指标反映的是不同环节所提供阻尼转矩的大小,3%为特殊情况下的差异数值,该临界条件下AGC 和PFR 环节对振荡模式的影响非常接近。在该场景下,本文的模式判据仍然有效,验证了本文方法的适用性。

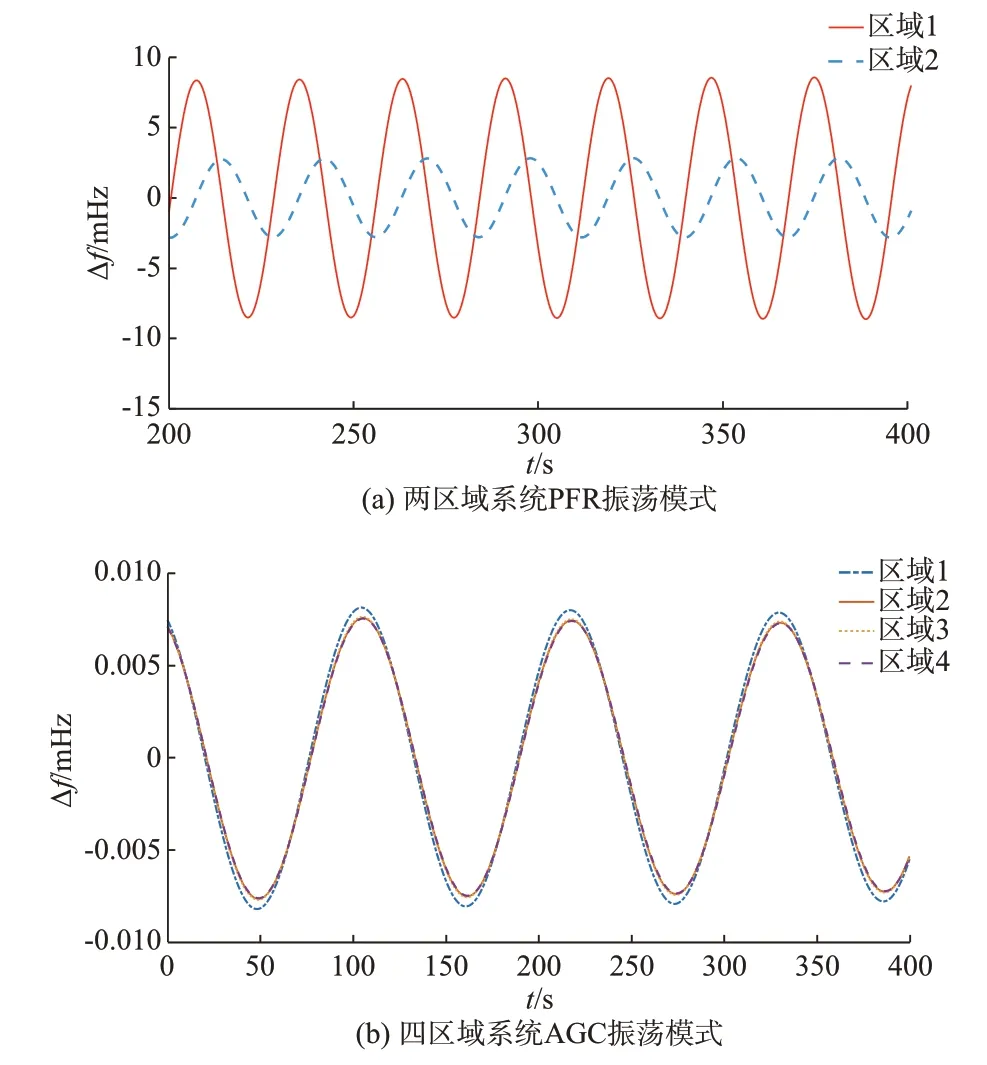
在图3（a）振荡模式下,图3（b）给出了系统PFR和AGC 的功率调节指令。结果表明,在该振荡模式下PFR 主要参与动作,与上文中模式辨别指标结果一致。

图3 单区域频率振荡分析Fig.3 Single-area frequency oscillation analysis

图3（c）为单区域系统AGC 振荡曲线图。对振荡曲线进行Prony 分析,得到系统振荡主导模式的幅值为9.641 3×10-5Hz,相位为3.835 7 rad,频率为0.036 1 Hz,阻尼比为0.226 8。其特征值分析结果如表2 所示。其中,模式1 为主导模式,计算模式辨别指标为Ddamp,PFR=7.620 3 和Ddamp,AGC=8.111 2,得到Ddamp,PFR

图3（d）给出了该模式下,系统PFR 和AGC 的功率调节指令。在该振荡模式下,AGC 主要参与动作,为AGC 模式,与模式辨别指标结果一致。其中,PFR 与AGC 的功率调节指令存在相位差,是由于AGC 过程中时滞环节和ACE 带来的相位偏移,并不属于普遍规律。

对PFR 振荡和AGC 振荡进行参数影响分析,具体分析结果如附录B 所示。综合分析可知,不合理的AGC 和PFR 参数设置会导致系统发生相应模式的频率振荡,本文提出的模式辨别指标可以有效辨别振荡模式,与功率指令判断的结果一致。

3.2 多区系统验证

本节在多区域AGC 系统中进行时域仿真,分析模式辨别指标在多区域AGC 系统的适用性,通过时域仿真分析验证模态辨别结果的正确性和可行性。

首先,在附录A 图A2 所示的两区域AGC 系统进行了仿真分析,参数设定见附录A 表A2,振荡表现为减幅振荡接近等幅振荡,如图4（a）所示。

图4 多区域频率振荡分析Fig.4 Multi-area frequency oscillation analysis

系统在该振荡模式主导时的特征值为0.000 1±i0.225 2,频率为0.035 8 Hz,Ddamp,PFR=0.886 0,Ddamp,AGC=0.016 6,阻尼比为-0.000 5。其中,模式辨别指标Ddamp,PFR>Ddamp,AGC,得出在该两区域系统为PFR 振荡,PFR 过程提供了更多的阻尼转矩。同时,计算该振荡模式下的AGC 功率调节比为ψ=0.038 2<0.5,为PFR 模式,与模式辨别指标的计算结果一致。

进一步,针对四区域AGC 系统进行仿真与验证,四区域系统图见附录A 图A3,参数设定见附录A 表A3,振荡曲线如图4（b）所示。系统在该振荡模式主导时的特征值为-0.000 2±i0.058 8,频率为0.008 9 Hz,Ddamp,PFR=1.491 3,Ddamp,AGC=14.067 1,阻尼比为0.002 8。其中,模式辨别指标Ddamp,AGC>Ddamp,PFR,可以得出在四区域系统发生AGC 振荡时,AGC 过程为发电机提供了更多的阻尼转矩。计算该振荡模式下的AGC 功率调节比为ψ=4.051 7>2,为AGC 模式,与模式辨别指标的计算结果一致。

为进一步验证本文提出的模式辨别指标的鲁棒性和适用性,分别在不同系统、机组和参数变化下进行验证。不同场景下的模式辨别指标辨别结果如表3 所示。

表3 不同场景下的模式辨别结果Table 3 Mode identification results in different scenarios

通过调整参数,使系统由PFR 或AGC 主要参与动作,最后两个场景考虑AGC 噪声影响,含噪声系统设置参考文献［28］,仿真结果见附录A 图A4。模式辨别指标方法适用于多变的不同场景,该方法反映的是两个动态调频过程提供的阻尼转矩对系统振荡的影响,其数值可能会随着具体设定的参数变化有所改变,但不影响最终辨别结果。

3.3 实际系统验证

本节在PSASP7.41 软件中构建3 机9 节点系统,该系统模型和参数设置见文献［29］。由于频率振荡通常发生在水电主导的系统中,将3 台机组均设置为水电机组,具体参数如表4 所示。

表4 3 机9 节点仿真系统参数Table 4 Parameters of 3-machine 9-bus simulation system

在t=10 s 时进行切负荷实验,发生频率振荡,得到频率振荡曲线如图5 所示。根据本文方法分析得到系统在该振荡模式主导时的特征值为-0.008 9±i0.496 7,频率为0.079 1 Hz,Ddamp,PFR=0.072 7,Ddamp,AGC=0.007 3,阻尼比为0.017 9。其模式辨别指标为:PFR 环节阻尼系数Ddamp,PFR=0.072 7,AGC 环节阻尼系数Ddamp,AGC=0.007 3。由于Ddamp,PFR>Ddamp,AGC,可知PFR 提供更多的阻尼转矩,该振荡为PFR 振荡。

图5 系统频率振荡曲线Fig.5 System frequency oscillation curve

综合以上分析,本节内容进一步验证了DTA方法在频率振荡领域的适用性。本文提出的模式辨别指标可以有效和正确地辨别实际系统中的PFR振荡模式和AGC 振荡模式,为系统频率振荡时采取及时、有效的抑制措施提供理论依据。

4 结语

本文提出了适用于电力系统频率稳定分析的DTA 方法,能够分析系统中不同调频过程动态对频率振荡的影响及阻尼转矩的分配和传递机理。基于DTA 提出频率振荡模式辨别方法,定义模式辨别指标,可以快速辨别与分析频率振荡模式,并进行仿真分析与结果验证。本文的主要工作与结论如下:

1）本文以传统的低频振荡DTA 理论为基础,建立了适用于频率稳定分析的阻尼转矩理论。揭示了PFR 和AGC 控制过程向系统中发电机提供阻尼转矩的过程,进而由发电机的阻尼转矩贡献转化为对振荡模式阻尼的影响,由此解释了频率振荡的影响机理。

2）与已有的模式辨别方法相比,模式辨别指标能够有效反映不同调频环节对振荡模式提供的阻尼大小,无须根据专家经验设定范围,辨别判据较为清晰、直观,对于不同场景和运行条件均能有效应用,且鲁棒性强,能够给实际电网中的频率振荡事件提供理论参考。

3）当水轮机水锤效应时间常数和调差系数比例增加时,PFR 振荡会加剧,表明水轮机调速系统在频率振荡超低频段呈现出比较明显的负阻尼特性。AGC 控制器KI参数和频率偏差系数增加时,阻尼比降低,均不利于系统的频率稳定。

4）本文方法在多区系统中也得到了验证。多区系统仿真结果显示,频率振荡呈现出全系统同调变化的特征,与目前实际电网案例情况一致,如何从理论上进行解释需要进一步的研究。

本文在撰写过程中得到新能源与储能运行控制国家重点实验室开放基金项目(NYB51202201704)的帮助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。