新能源场站分布式同步调相机暂态功角稳定性影响因素分析

赵天骐，李秉芳，杨松浩，谢 欢，张 隽，吴 涛

（1.国网冀北电力有限公司电力科学研究院（源网荷储灵活运行与协调控制国家电网公司实验室）,北京市 100045；2.西安交通大学电气工程学院,陕西省西安市 710049；3.国网冀北电力有限公司电力调控中心,北京市 100054）

0 引言

构建新型电力系统是推动实现中国“双碳”战略的重要举措。然而,目前新能源,尤其是风电大规模开发和大功率送出面临并网短路比低、电压支撑能力弱的制约［1］。同步调相机具备良好的瞬时动态无功响应特性和提供短路容量支撑的能力,在新能源场站部署调相机可改善新能源送端由低短路比引发的电压振荡与暂态过电压等问题［2-5］,对支撑电网强度和促进新能源消纳效果显著。因此,“新能源与调相机”组合成为目前国家电网公司正在大力推行的新型发电组合。

同步调相机作为一种特殊的同步电机,可能引发系统的同步稳定性问题。在传统认知中,同步调相机/同步电动机静态稳定裕度很大,一般不会发生加速失步,只可能在大扰动下因动态失稳而发生减速失步［6-7］。但最近的研究表明,安装于新能源场站的同步调相机受新能源的影响,存在故障后功角加速失稳的风险。文献［8］提出了新能源场站中调相机的加速失稳现象,并分析了该弱送端电网在送出通道发生故障时的功角稳定性。文献［9］进一步研究了考虑新能源暂态特性的调相机失稳形态,通过注入电流源的方式揭示了新能源稳态出力及低电压穿越控制对调相机功角稳定性的影响机理,并指出新能源采用低电压穿越控制后,同步调相机均有暂态功角加速失稳的风险,需要在新能源送出系统的配置规划及运行控制中予以考虑。

目前,国内外已有大量针对新能源电力系统中同步发电机暂态功角稳定性的关键影响因素分析的研究成果。文献［10］基于直流潮流模型,定性地分析了同步机出力调整、风电场选址、风电渗透率等因素对电力系统暂态稳定性的影响规律。文献［11］通过仿真证明了风电等容量置换同步机,可提高系统的暂态稳定性。文献［12］指出风电比例对送端系统功角稳定性的影响规律同受端系统强弱有关。文献［13］分析了双馈风电机组直接接入和代替同容量同步发电机接入系统2 种方式下对系统暂态功角稳定性的影响差别。文献［14］指出系统暂态稳定性同故障位置有关,当故障发生在风电场附近时,系统转子角振荡显著加剧。此外,新能源的暂态控制特性也会对系统功角稳定性产生影响。文献［15］建立了光伏与风电系统的低电压穿越控制模型,通过仿真证明了若新能源无故障穿越能力,则系统中同步发电机更容易发生暂态功角减速失稳。文献［16］构建了双馈风电机组接入系统后的等值单机-无穷大系统模型,基于等面积准则阐明了故障清除后风电机组有功出力恢复速率的减慢在提升系统首摆稳定性的同时会导致二摆失稳。文献［17］通过进一步研究提出双馈风电机组的有功出力恢复控制在加剧系统首摆与奇数次多摆失稳可能性的同时,可抑制偶数次多摆失稳现象的发生。文献［18］分析表明当改变故障后风电机组有功出力恢复速率时,风电接入对系统暂态功角稳定性的正面（或负面）影响性质保持不变,但是影响程度不同。文献［19］通过电磁暂态仿真,论证了故障清除后风电机组有功出力的快速恢复特性会降低系统的暂态稳定水平。

上述文献对新能源电力系统功角稳定性的影响因素开展了深入研究并获得了有益结论,但由于新能源场站中同步调相机暂态失稳形态与同步机存在显著差别,故相关结论无法直接应用。本文针对这一问题,在文献［9］的基础之上,进一步讨论系统网架、同步调相机参数和新能源控制策略等因素对调相机暂态稳定性的影响,并通过新能源送出系统简化模型和含新能源和调相机的多机系统进行了仿真验证。

1 稳定分析模型及量化评价指标

1.1 稳定分析模型

含同步调相机的新能源送出系统拓扑结构如图1（a）所示。图中:同步调相机与新能源电源并入同一母线,送端功率经1 条单回线路和1 条双回线路送入负荷。同步调相机与远端同步系统构成了典型的两机系统。

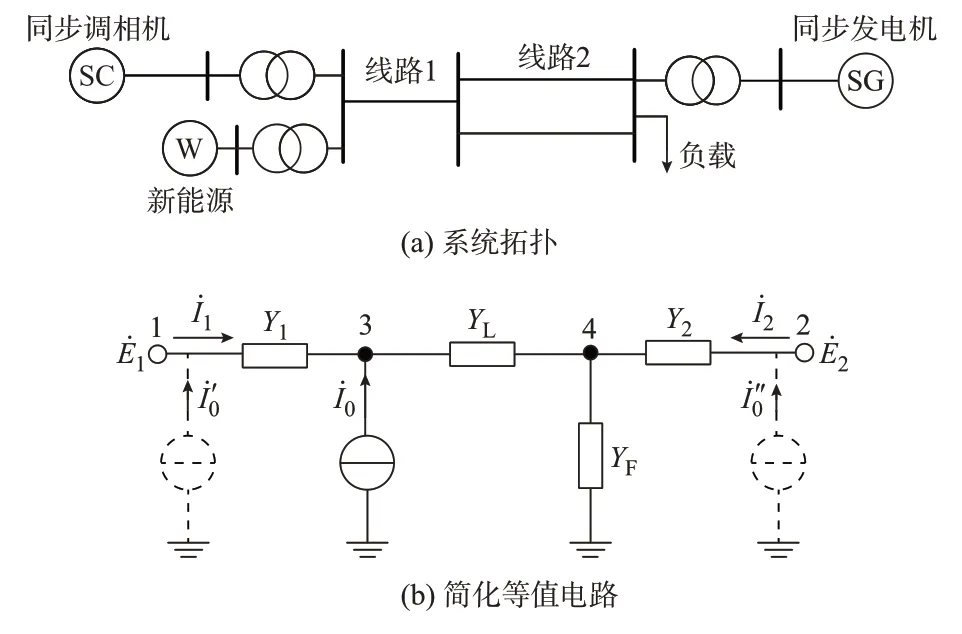
图1 含同步调相机的新能源送出系统Fig.1 Renewable energy sending-end power system with synchronous condenser

该两机系统的简化等值电路图如图1（b）所示,其 中,分 别 为 送 受 端 同 步 机 的 暂 态 电 势；İ1和İ2分别为送受端同步机注入节点1 和节点2 的电流；Y1、Y2、YL和YF分别为送端、受端、输电部分及负荷的等值导纳。新能源以电流源İ0并网,消去中间节点后等效注入调相机节点和系统发电机节点的电流分别 为,其表达式为:

将两机系统等值为调相机相对于发电机的单机-无穷大系统,其转子运动方程为:

式中:δ为调相机相对于系统的功角；Meq为两机系统的等值惯量；PM和PE分别为调相机相对于系统的等值机械功率和电磁功率；M1和M2分别为调相机和同步发电机的惯性时间常数；PMC和PMG分别为调相机、发电机的机械输入功率；G11和G22分别为节点1 和2 的自导纳；E1和E2分别为送受端同步机的暂态电势幅值；|Y12|为节点1 与节点2 之间转移导纳的模值；P′E为自导纳对PE的影响量；P〃E为新能源有功功率注入对PE的影响量；Re（·）为求实部的函数。推导过程见附录A。

由文献［9］可知,同步调相机的暂态功角稳定性受新能源稳态和暂态有功出力大小的影响。稳态时新能源有功出力的增大会使调相机的静态稳定裕度下降。而新能源低电压穿越深度（低电压穿越深度越深代表故障中保留的有功电流越小,如附录A 图A1 所示）的不同则会改变调相机的暂态功角摇摆形态。调相机2 种暂态功角摇摆形态如图2 所示。图2 中:PE1、PE2、PE3分别为短路前、短路中、短路清除后调相机等值电磁功率；δ0和δc分别为短路开始与清除时刻调相机的等值功角；δh和δj分别为故障清除后两机系统稳定平衡点和不稳定平衡点所对应的功角。定义调相机功角增大的方向为功角摇摆的正方向,在低电压穿越深度较浅时,故障发生后调相机首摆功角正向摆动,如图2（a）所示；在低电压穿越深度较深时,短路期间及故障清除后的一段时间内调相机功角反向摆动（此时点abcg围成的面积等于点defg的面积）,e点之后功角正向摆动,如图2（b）所示。

图2 同步调相机暂态功角摇摆形态Fig.2 Transient rotor-angle swing patterns of synchronous condenser

定义Sabcg、Sdefg、Sdgh、Sefh、Shij分别为由点abcg、点defg、点dgh、点efh、点hij围成的面积,亦可表征暂态能量。从图2 可知,尽管调相机在短路期间功角减小,但其暂态总加速面积增大:一方面,由于Sabcg=Sdefg,故可将短路期间的减速能量Sabcg视为加速能量；另一方面,故障清除时刻的功角δc越小,则加速面积Sefh越大,呈现出“弹簧效应”,即短路期间的减速是为短路清除后的加速而“蓄力”。

1.2 影响因素量化评价指标

新能源外送单回线路上发生单相接地短路故障后非全相运行场景,具有发生概率高、危害性大、代表性强的特点（分析见附录B）。因此,本文将针对这一典型场景,对新能源场站调相机首摆功角反向摆动时的暂态功角稳定性进行理论分析与仿真验证。为量化评价各影响因素对调相机功角稳定性的影响,本文提出暂态稳定裕度指标ΔS。

由于调相机没有原动机,故其稳态有功出力近似为0。由式（4）可知,等值单机-无穷大系统的机械功率为:

短路期间的加速能量S1为:

非全相运行期间的暂态加速能量S2为:

非全相运行期间的最大暂态减速能量S3为:

定义暂态稳定裕度ΔS为最大减速能量与总加速能量之差,即:

ΔS增大,表明调相机的功角稳定性变好；反之,若ΔS减小,则代表调相机的功角稳定性变差。在调相机保持暂态稳定时,也可以用首摆时最大摇摆角δmax表征其功角稳定性大小,δmax越大,功角稳定性越差。

2 影响因素分析

2.1 新能源-调相机与系统侧的电气距离

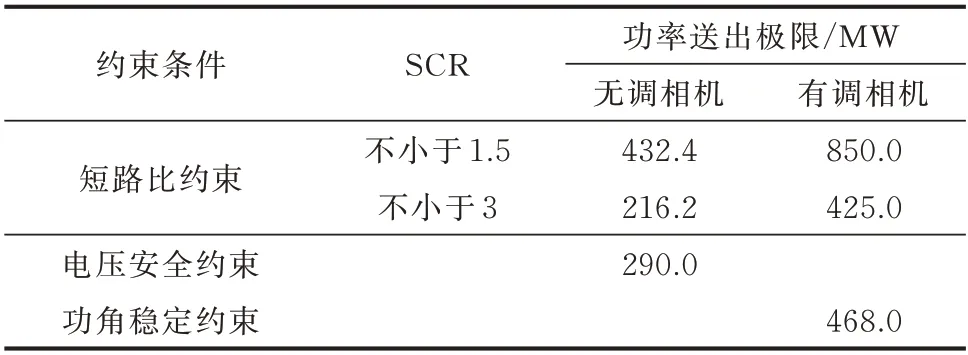
新能源距离系统等值发电机的电气距离增大后,Y12减小,而且由式（1）可知,Y2或YL的减小会使İ′0增 大,İ〃0减小。进而根据式（5）和式（7）可知,PE1、PE2和PE3均 会 下 移（下 移 后 的 曲 线 为P′E2和P′E3）,导致故障前调相机稳定运行点所对应的功角δ0、短路清除时刻所对应的功角δc及加速结束时刻功角δh右移,最大减速面积处所对应的功角δj稍右移（如图3（a）和图3（b）所示,其中,电气距离D′

图3 各因素对同步调相机暂态功角稳定性的影响Fig.3 Influence of various factors on transient rotorangle stability of synchronous condenser

当短路中调相机功角反向摆动时,由于低电压穿越期间新能源有功电流较小,PE2减幅不大,故S1可看做近似不变。对于非全相运行期间的加速能量S2和 减 速 能 量S3,有δh-δc>0、δj-δh>0 及cosδh-cosδj>0,根据式（10）和式（11）可知,S2增大,S3减小,从而ΔS减小。因此,当新能源与系统侧的电气距离增大时,同步调相机的功角稳定性将显著降低。

2.2 调相机惯量

同步电机惯性时间常数的定义是在同步机的转轴上加额定转矩后,转子从停顿状态加速到额定转速所需要的时间。本文以惯性时间常数作为系统惯量的表征指标。

当M1≪M2时,由式（5）和式（8）可得到:

当M1变化时,调相机等值电磁功率与机械功率曲线的相对位置没有改变,即S3不变。由式（2）可知,Meq越小时,越大。设故障持续时间为T,则有

式中:ω0为初始时刻调相机的角速度。

2.3 新能源暂态控制策略

2.3.1 新能源低电压穿越控制深度

为保证系统发生故障后新能源机组能够不间断并网运行,要求新能源机组具备故障期间减发有功出力的低电压穿越能力。新能源低电压穿越深度越深,表示故障期间新能源保留有功出力越小。根据式（1）、式（5）和式（7）,当网络拓扑参数确定时,调相机等值电磁功率的大小主要取决于新能源注入电流,所以 故障期间 新能源有 功电流越大,即低 电压穿越深度越浅,PE2曲线下移程度就越大。从式（2）和式（14）可知,如果短路时间相同,|PE2-PM|越大,则故障清除时刻所对应的功角δc相对于故障前稳定运行点δ0的变化量,即|δc-δ0|也就越大。这表明随着低电压穿越深度从深到浅,短路中PE2曲线由上至下移动（下移后的曲线为P′E2,对应的运行点为也随之由小变大。

图3（e）和图3（f）是用等面积准则解释低电压穿越深度变化对暂态能量影响的示意图,其中,低电压穿越深度′′。当低电压穿越深度从深到浅变化时,δc-δ0增大,δh-δc和PE2减小。若短路期间调相机功角减小,则有δc-δ0<0,δh-δc>0,cosδh-cosδj>0,这 时 低 电 压 穿 越 深 度 的 降 低 会使S1和S2均减小。因为低电压穿越深度的变化不会引起PE3的改变,所以S3不变,故而调相机稳定性增强。

因此,随着低电压穿越深度由深变浅,调相机的暂态功角稳定性会得到提升。

2.3.2 新能源有功出力恢复速率

在实际系统中,新能源有功出力恢复的快慢取决于其控制策略。如附录A 图A1 所示,Vi,i=0,1,2,3,为故障清除后新能源有功出力恢复速率,且有V3

随着新能源有功出力恢复速度的减小,PE的变化情况如图3（g）至图3（j）所示,此时,实际上的PE不仅仅是δ的函数,也是时间的函数,会沿着设定恢复速率下的曲线组和既定的功角特性轨迹变化。图3（g）至图3（j）中,PE3为新能源有功出力完全恢复后的曲线,均为未完全恢复时的曲线。如图3（g）所示,在故障清除瞬间,由于系统由单相故障变为非全相运行状态,调相机的有功出力运行点从c点跳变到k点。在下一时刻,若新能源有功出力可以立即恢复,则运行点又会立刻变为d点,此后沿着PE3先左移后右移变化；而当恢复速率减慢时,运行点跳变到k点之后会沿随时间下移的PE曲线缓和地变化,如图3（h）所示。

如图3（h）、图3（i）和图3（j）所示,在恢复速率分别为V1、V2、V3时,对应的总加速能量S1+S2可以分 别 表 示 为:Sabcg′+Sd′g′h′、Sabcg″+Sd″g″h″以 及Sabcg‴+Sd‴g‴h‴；最 大 减 速 能 量S3可 分 别 表 示 为:Sh′i′j′、Sh″i″j″以及Sh‴i‴j‴,以上变量均表示由其下标字母所表示的点围成的面积。当恢复速率由V0减小为V1时,在故障清除后调相机的等值功角会沿逐步跌落的PE曲线继续减小。若调相机PE曲线的运行点到达使Sabcg′=Sd′f′g′的′点时,新能源有功出力 还未完 全恢复,则下一时刻调相机运行点继续沿着恢复中的PE曲线组变化,功角正向摆动。与立即恢复相比,以速率V1恢复时,S1+S2与S3均会增大,但调相机减速阶段时新能源有功出力的恢复程度要大于加速阶段,这就使得减速面积的增幅小于加速面积的增幅,即ΔS3<ΔS1+ΔS2。因此,新能源有功出力恢复速率从V0变为V1后,调相机的暂态功角稳定性变差（如图3（g）到图3（h）所示）。

当新能源恢复速率进一步减小至V2乃至V3（趋近于0 s-1）时,这一阶段S3仍在增大,理论上的最 大 值 为Sh‴i‴j‴,但 加 速 能 量S1≤Sabcg‴=Sd‴f‴g‴

因此,故障清除后新能源有功出力从立即恢复到减慢恢复速率,调相机的暂态功角稳定性先降后升。

3 仿真验证

3.1 含调相机的新能源送出简化系统

在PSD-BPA 软件仿真平台上构建新能源送出简化仿真系统,如附录C 图C1 所示。其中,分布式调相机总容量为150 MV·A,额定电压为10.5 kV,惯性时间常数为5 s；等值发电机容量为1 500 MV·A、惯性时间常数为20 s；新能源为直驱风力发电机,并入0.69 kV 母线,总装机容量为550 MV·A,实际有功出力为450 MW。新能源场站内安装同步调相机,二者汇集于35 kV 母线后,经220 kV 单回线路和500 kV 双回线路输送至负荷。负荷为恒阻抗模型,额定功率为500 MW。电气距离、调相机惯量、新能源低电压穿越深度及有功出力恢复速率的参数变化情况见表1,其中,电气距离的标幺值以同一基准容量1 000 MV·A 归算。设置故障为0.5 s 时220 kV 线路电源侧处发生单相瞬时故障,100 ms 后保护动作将故障相切除,再经1 s 后重合。

表1 简化系统关键仿真参数Table 1 Key simulation parameters of simplified system

在上述条件下进行仿真,得到在送受端电气距离、调相机惯量、新能源低电压穿越深度及恢复速率变化时调相机的等值功角随时间变化的曲线,如图4 所示。上述4 种影响因素分别对应图4（a）、图4（b）、图4（c）和图4（d）,图中t为时间变量。

图4 不同影响因素下的功角曲线Fig.4 Rotor-angle curves with different influence factors

从图4（a）可知,新能源距离系统的电气距离增大后,调相机稳态运行点所对应的功角增大,最大摇摆角δmax也随之增大,当电气距离为1.54 p.u.时,调相机功角失稳。这表明调相机的暂态功角稳定性随新能源与系统电气距离的增加而变差。

图4（b）表明,调相机惯量对初始稳定运行点没有影响。M1越大,短路结束时刻的功角δc的绝对值越小,首摆时的δmax也越小,调相机的暂态功角稳定性呈现出随惯量增大而增大的趋势。仿真结果与前述理论分析相一致。

图4（c）是当新能源低电压穿越深度从80%降至30%时同步调相机的功角曲线。该图表明,新能源低电压穿越深度从深到浅变化时,调相机暂态功角从失稳（低电压穿越深度为80%）变为稳定（低电压穿越深度为30%～70%）。以δmax的大小来衡量,在低电压穿越深度变浅的过程中,调相机功角稳定性逐渐增强。

新能源有功出力恢复速率变化时调相机等值功角曲线如图4（d）所示。当恢复速率V≥100% s-1时,恢复速率越小,调相机首摆功角减小得越多,则次摆最大摇摆角δmax增幅就越大,因而暂态稳定性也就越差。当新能源有功出力用时0.5～1 s 恢复时,调相机功角失去稳定；但当V≤50% s-1时,反向摆动时的最小功角基本不再变化。同时,S3的增大使得δmax较之立即恢复时不断减小。因此,随着恢复速率减慢,调相机的功角稳定性会先减小后增大。

3.2 含新能源与调相机的多机系统

为验证新能源低电压穿越控制策略对调相机功角稳定性的影响在多机系统中的适应性,构建了如附录C 图C2 所示的含新能源与调相机的多机系统。该系统在IEEE 10 机39 节点标准系统的基础上进行修改,用风电场加调相机替代39 号母线上的同步发电机。其中,新能源有功出力为650 MW,调相机容量为150 MVA,低电压穿越深度设为10%～100%和50%,新能源有功出力恢复速率设为立即恢复和0（立即恢复）～50% s-1。故障设置为1 s 时母线38 与母线29 之间的单回线路发生单相接地短路,100 ms 后保护动作将故障相切除,再经1 s 后重合。仿真结果如附录C 图C3 所示。由图C3 可知,若首摆反向摆动时,随着低电压穿越深度的变深,调相机功角稳定性变差；随着恢复速率的减小,调相机的功角稳定性先降低后提升。上述仿真结果与理论分析结果相一致,验证了所得结论在多机系统的适应性。

4 功角稳定约束下新能源功率送出极限及影响因素灵敏度分析

4.1 功角稳定约束下新能源功率送出极限

新能源场站功率送出极限由多因素决定,工程上常采用短路比（short circuit ratio,SCR）等指标进行估计。短路比是评价系统电网强度、评估新能源功率送出极限的实用综合指标。相关研究表明［20-21］,新能源并网系统电压支撑能力较弱,当故障清除后,新能源汇集地区易出现暂态过电压或机组反复低电压穿越的现象,甚至导致连锁脱网事故。因此,故障后的电压安全问题是目前限制新能源场站功率送出极限的主要因素。若在新能源场站安装分布式调相机,利用调相机瞬时动态无功支撑与短路容量支撑的能力,可以提高新能源的功率送出极限。但是,由本文分析可知,新能源影响下的调相机面临功角失稳风险,同样存在约束新能源有功出力的可能。

表2 给出了新能源场站在有和无调相机2 种场景下受不同约束的功率送出极限,系统参数与3.1节相同。由表2 可知,当不安装调相机时,受电压安全及短路比的约束,新能源场站功率送出极限为216.2～290.0 MW,此时不存在功角稳定约束。若按照3.1 节中的参数配置同步调相机,则短路比约束下新能源场站的送出功率极限可提升至425.0～850.0 MW；考虑新能源容量限制及输电通道的热稳定制约时,新能源场站功率送出极限为550 MW；在调相机功角稳定约束下,新能源场站的功率送出极限为468.0 MW。这一结果说明在新能源场站中增设调相机可以显著增加新能源场站在电压安全或短路比约束下的出力极限,但是调相机的功角稳定性或将成为限制新能源出力的主要约束之一。因此,分析功角稳定性约束下的新能源送出功率极限,对保障新能源场站送出系统安全稳定运行具有指导意义。

表2 不同主导约束条件下新能源功率送出极限Table 2 Power dilivery limits of renewable energy under different dominant constraints

4.2 影响因素灵敏度分析

为进一步挖掘新能源场站功率送出潜力,提高新能源功率送出水平,现对影响调相机暂态功角稳定性因素进行灵敏度分析。对各个影响因素进行标幺化处理（正常运行状态下的数值为基准值,而新能源有功出力恢复速率选取100% s-1为基准,得到各影响因素与新能源功率送出极限关系,如图5所示。

图5 影响因素对新能源功率送出极限的灵敏度比较Fig.5 Sensitivity comparison of influence factors on power delivery limits of renewable energy

图5 中曲线的斜率体现了新能源功率送出极限对不同影响因素的灵敏度。由图5 可知,新能源功率送出极限对电气距离与新能源有功出力恢复速率变化最敏感,低电压穿越深度次之,对调相机惯量变化的敏感度最低。从曲线的变化来看,新能源有功出力恢复速率对新能源功率送出极限的影响最为显著。新能源出力恢复速度从立即恢复降速至100% s-1恢复速率时,新能源功率送出极限持续下降,当恢复速度降低至100% s-1时,送出极限最低,共降低了42 MW。若恢复速度进一步降低,则新能源功率送出极限开始提升,当恢复速度持续降低至30% s-1时,新能源功率送出极限最大为550 MW,较立即恢复时提升了82 MW。新能源低电压穿越深度从30%变化至80%时,新能源功率送出极限从477 MW 降至433 MW。在合理变化范围内,调相机惯量的影响程度最小:惯量从2 s 增至6 s,送出极限的变化量仅为11 MW。

图5 也直观地反映了新能源控制策略对调相机功角稳定性的影响,可为制定新能源控制策略提供参考。整体而言,低电压穿越深度较浅时,调相机的功角稳定性较强,但也增加了新能源定子变流器在短路过程中的过电流风险。因此,建议在变流器耐流能力范围内,尽量降低新能源的低电压穿越深度。另一方面,新能源有功出力恢复很快或很慢均有利于提升调相机的功角稳定水平,但考虑到新能源自身的功率平衡,建议采用较快的有功出力恢复速率。

需要说明,在线路2 三相短路故障过程中,最不利低电压穿越深度下的新能源功率送出极限为650 MW,显著高于线路1 单相短路故障对新能源功率送出极限的约束。这也证明了对于新能源与调相机送出系统,本文所讨论的送出线发生单相故障场景具有典型性。

通过上述分析可知,功角稳定约束下的新能源场站功率送出极限对新能源暂态控制等可控因素具有较高的灵敏度。因此,改进新能源暂态特性以提升新能源功率送出极限具有很好的潜力。

5 结语

在新能源场站配置同步调相机可提升新能源并网强度,但同时引入了调相机的暂态功角稳定约束。本文分析了影响调相机功角稳定性的关键因素,旨在为其运行规划及控制策略的制定提供理论基础,以期进一步提升新能源的送出水平。得到以下主要结论。

1）新能源距系统侧电气距离越大,新能源有功电流会对调相机的暂态稳定性产生越不利的影响。调相机的暂态功角稳定性随其惯量的增大而增大,但影响程度较小。

2）新能源的控制策略会对调相机的暂态稳定性产生影响。当调相机首摆功角反向摆动时,随着低电压穿越深度从深到浅变化,调相机功角稳定性变好；故障清除后新能源有功电流以恒速率斜坡恢复使调相机功角稳定性随新能源有功出力恢复速率的减慢先下降后提升。

需要指出,本文结论建立在一定理想假设及模型简化基础上,可定性地反映该典型场景下的稳定形态和影响因素,而欲定量求解实际新能源与调相机系统在功角稳定性约束下的功率送出极限,还需借助更加精细的系统级建模和更大规模的仿真验证。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。