虚拟调速器对VSG暂态功角稳定影响机理分析
张 巍,黄 文,帅智康,葛 俊,沈 超,程慧婕,沈 霞
(1. 湖南大学国家电能变换与控制工程技术研究中心,湖南长沙 410082;2. 东南大学电气工程学院,江苏南京 210096)
0 引言
为了应对能源危机和环境污染,大量新能源如太阳能、风能通过电力电子变换器连接到电网中,大幅降低了电网的惯性水平[1]。为了补偿系统的惯性损失,虚拟同步发电机VSG(Virtual Synchronous Generator)受到了广泛关注[2]。VSG 由于其控制系统中添加了转子运动回路、虚拟调速器VG(Virtual Governor)回路、无功控制回路等环节,能模仿同步发电机的输出特性,具有惯性支撑、频率调节和电压控制的能力[3]。然而,与同步发电机类似,在大扰动下由于输入机械功率与输出电磁功率的不平衡造成加速面积大于减速面积,VSG 也将面临严重的暂态稳定性问题[4]。国内外学者对此开展了大量研究。从暂态稳定分析方法来看,现有研究方法主要有5种,即数值时域法[5]、李雅普诺夫能量函数法[6]、相图法[7]、等面积法[8]和人工智能法[9⁃10]。从暂态稳定性机理来看,很多学者致力于VSG 的转子运动回路[7,11⁃13]、无功控制回路[6,8]以及限流控制[14⁃16]等方面的研究。文献[7]指出由于转子运动回路含有惯性环节,即使存在平衡点也可能出现暂态不稳定的现象。文献[11]详细分析VSG 同步丢失的机理,并提出一种暂态阻尼,避免文献[7]中暂态稳定和频率稳定的冲突。文献[12]提出一种模式自适应功角控制方法,将转子运行回路在正反馈和负反馈间自适应切换,提高了VSG 暂态稳定,但忽略了阻尼影响,结果偏保守。研究发现,单回路电压幅值控制对VSG的暂态稳定性具有重要影响[13]。文献[6]指出无功控制回路由于正反馈效应会恶化VSG 变换器的暂态稳定性。文献[8]指出不同的无功回路对VSG 暂态稳定性的影响程度不同。文献[14]发现电网故障期间的电流饱和可能造成VSG 控制瞬态不稳定。文献[15]对含虚拟电阻的VSG 暂态稳定进行分析,得出虚拟电阻与电网电阻相反、恶化暂态稳定性的结论。文献[16]揭示功率基准调整和暂态虚拟电阻控制对暂态稳定性的影响。在上述文献中,暂态稳定性被认为仅由转子运动回路、无功控制回路、限流保护控制等决定。作为VSG 重要组成部分之一的VG,对有效调节输入机械功率起着至关重要的作用,其参数不仅影响系统频率和并联功率的分配,而且对VSG 暂态功角稳定有重要影响,但VG 对VSG暂态功角稳定的影响机理却少有研究。
调速器作为一次调频环节,对于系统安全稳定运行起着重要作用。同步发电机中的调速器对稳定性的影响已被广泛研究[17]。研究发现,暂态功角不稳定可能是大扰动下由调速器引起的机械转矩和电磁转矩间的不平衡造成的[18]。相较于同步发电机,由于VSG 具有更灵活的控制方式,因此可以通过合理设计VG 的结构和参数使系统在大扰动下更容易达到暂态稳定。目前典型的VG 主要包括高通滤波HPF(High-Pass Filter)型和低通滤波LPF(Low-Pass Filter)型2 种[19⁃21]。文献[19]采用HPF 型VG 来对系统频率进行主动控制,但未考虑其对暂态稳定性的影响。文献[20]提出一种比例积分型VG 模型。文献[21]发现采用LPF 型VG 的VSG(简称为LPF-VGVSG)来取代同步发电机可得到更好的稳定性能。事实上,LPF 型调速器与比例积分型调速器是等效的[18]。从上述文献分析可知,由于VG 的加入,VSG的动态响应与同步发电机接近,有利于同步发电机与VSG 并联系统的稳定运行。但上述文献均仅对加入VG 后的系统进行建模以及对负荷功率变化下的动态特性进行研究,而没有对动态特性的深层次影响机理进行分析,也没有考虑大扰动下VG对VSG暂态功角稳定的影响。文献[22]从VSG 与同步发电机并联的角度分析容易出现暂态功角失稳的原因,即同步发电机和VSG 的调速器差异,但没有对不同类型VG 下的系统暂态功角稳定进行深入分析。为了提高暂态稳定性,文献[23]提出一种基于HPF的暂态阻尼提升方法。文献[24]针对调速器模块常被忽视的现状,从截止频率的角度研究基于LPF 的调速器模块对VSG 大信号稳定性的影响,但没有从带宽、增益等多维度进行综合分析。虽然已有部分研究考虑了VG 模块对VSG 暂态功角稳定的影响,但没有研究考虑不同VG 对VSG 暂态功角稳定影响的机理,尤其是不同VG 对VSG 暂态稳定性影响的共性和区别需进一步进行分析。
首先,本文对不同VG 的VSG 进行大信号建模,得到不同VG 的VSG 大信号降阶模型;其次,通过扩展等面积定则EEAC(Extended Equal Area Criterion)分析得到不同VG 对VSG 暂态功角稳定的影响机理;然后,利用相图分析方法进一步量化研究不同VG控制参数对VSG暂态功角稳定的影响程度,得出不同VG 控制参数下的系统最优暂态功角稳定区间,并总结VG 整体设计原则;最后,通过仿真证明本文理论分析的正确性。
1 采用不同VG的VSG大信号模型
图1 为储能VSG 接入三相电网的典型拓扑结构与控制结构。利用脉宽调制(PWM)将功率从直流侧传送到交流侧,并由VSG 侧滤波电感Lf、滤波电容Cf和电网侧滤波电感Ll1构成的LCL 滤波器来降低输出电流和输出电压纹波。图中:Udc为直流侧电压,由于其受储能或前级变换器调节,不是本文的研究重点,因此在本文的分析中假设其为常数[11];LT为变压器等效电感;Rg和Ll2分别为线路侧电阻和线路侧电感;Lg为由Ll1、LT和Ll2共同构成的线路等效电感;uabc和ugabc分别为VSG输出电压和电网电压;P和Q分别为VSG 输出有功和无功;iabc为流入电网的VSG 输出电流;mabc为可控的三相正弦信号;θref和Uref分别为VSG 输出电压相角和幅值;P*为VG 输出的参考有功功率;P0为VSG 输出有功功率设定值;ω0为系统角频率设定值;Q0为VSG 输出无功功率设定值;U0为VSG输出电压设定值;ω为VSG虚拟角频率;Δω为ω与ω0的差值;X为LPF 或HPF 型VG 的传递函数;ΔP为VSG 输出功率调整值;J和DP分别为VSG 的虚拟惯性系数和虚拟阻尼系数;Dq为无功下垂系数;s为拉普拉斯算子;PCC为公共耦合点。
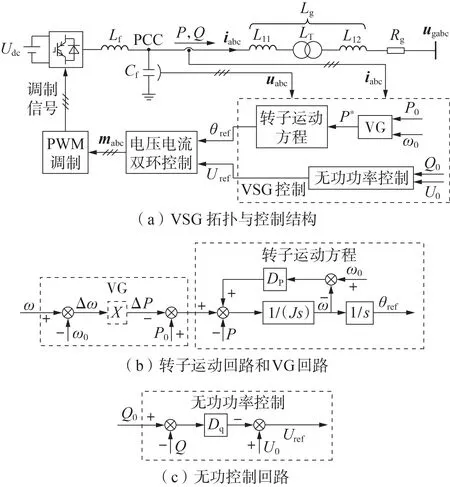
图1 VSG的拓扑结构和控制结构Fig.1 Topological structure and control structure of VSG
VSG 控制主要由转子运动回路、无功控制回路和VG 回路三部分组成。其中:转子运动回路和无功控制回路用于产生VSG 的θref和Uref,共同构成VSG 的内部输出电压;VG 回路主要是根据系统角频率差,通过X来调节P*,如图1(b)和附录A 图A1 所示。图A1 中:G为增益;ωc为截止角频率;和分别为采用LPF 和HPF 型VG 输出的参考有功功率。考虑到暂态稳定主要由功率控制回路和VG决定,本文采用快速动态的内部电压电流双环控制来保证uabc准确跟踪。
根据图1(b),VSG转子运动方程为:
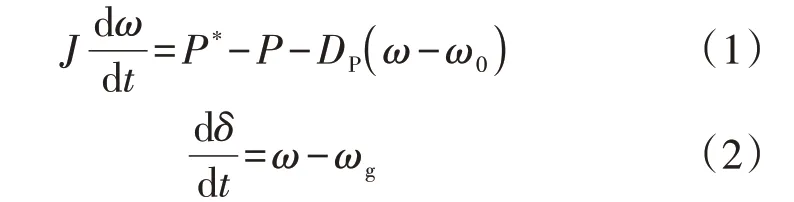
式中:δ为θref和电网电压相角θg之间的相角差,定义为功角;ωg为电网角频率,通常与ω0相等。
根据图1(c),VSG无功功率控制为:

根据图1(b),VG表达式为:

根据附录A 图A1,采用LPF 和HPF 型VG 的表达式分别为:
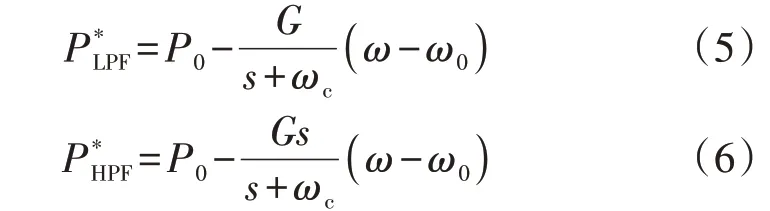
结合式(1)—(3)、(5),可得到采用LPF-VGVSG的控制表达式为:

结合式(1)—(3)、(6),可得到采用HPF 型VG的VSG(简称为HPF-VG-VSG)的控制表达式为:
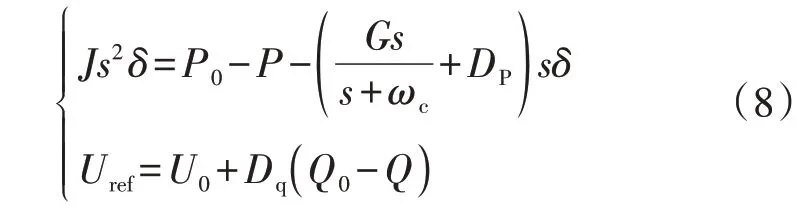
将电网电压ugabc作为参考,同时假定θg=0°,则θref=δ[7],因此,VSG 输出有功P和无功Q分别如式(9)、(10)所示。
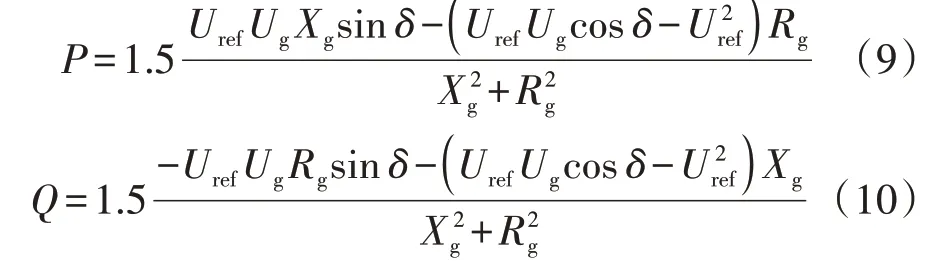
式中:Ug为电网电压幅值;Xg为线路等效电抗。
可以发现,P和Q通过δ和Uref相互耦合,将式(10)代入式(3),可推导出Uref(δ),再将其代入式(9)可得到考虑无功控制回路的P-δ关系为:

通过式(11)可绘制出具有不同Lg和Rg的P-δ曲线,如附录A 图A2 所示。可得出,当Lg较大或Rg较小时,由于允许变化的功角范围减小,因此不利于VSG暂态功角稳定。
由于VSG 控制可以用电压源表示来研究其暂态特性,本文分别建立LPF-VG-VSG和HPF-VG-VSG等效电路模型,如附录A图A3所示。
针对图A3中的LPF-VG-VSG和HPF-VG-VSG等效电路模型,分别令x3=G δ s/(s+ωc)和x3=G δ s2/(s+ωc),假设x=[x1,x2,x3]T,其中x1=δ,x2=ω-ωg=δ̇,在忽略时间尺度较小的电压、电流内环等环节影响下,2个等效电路模型的大信号降阶模型分别为:
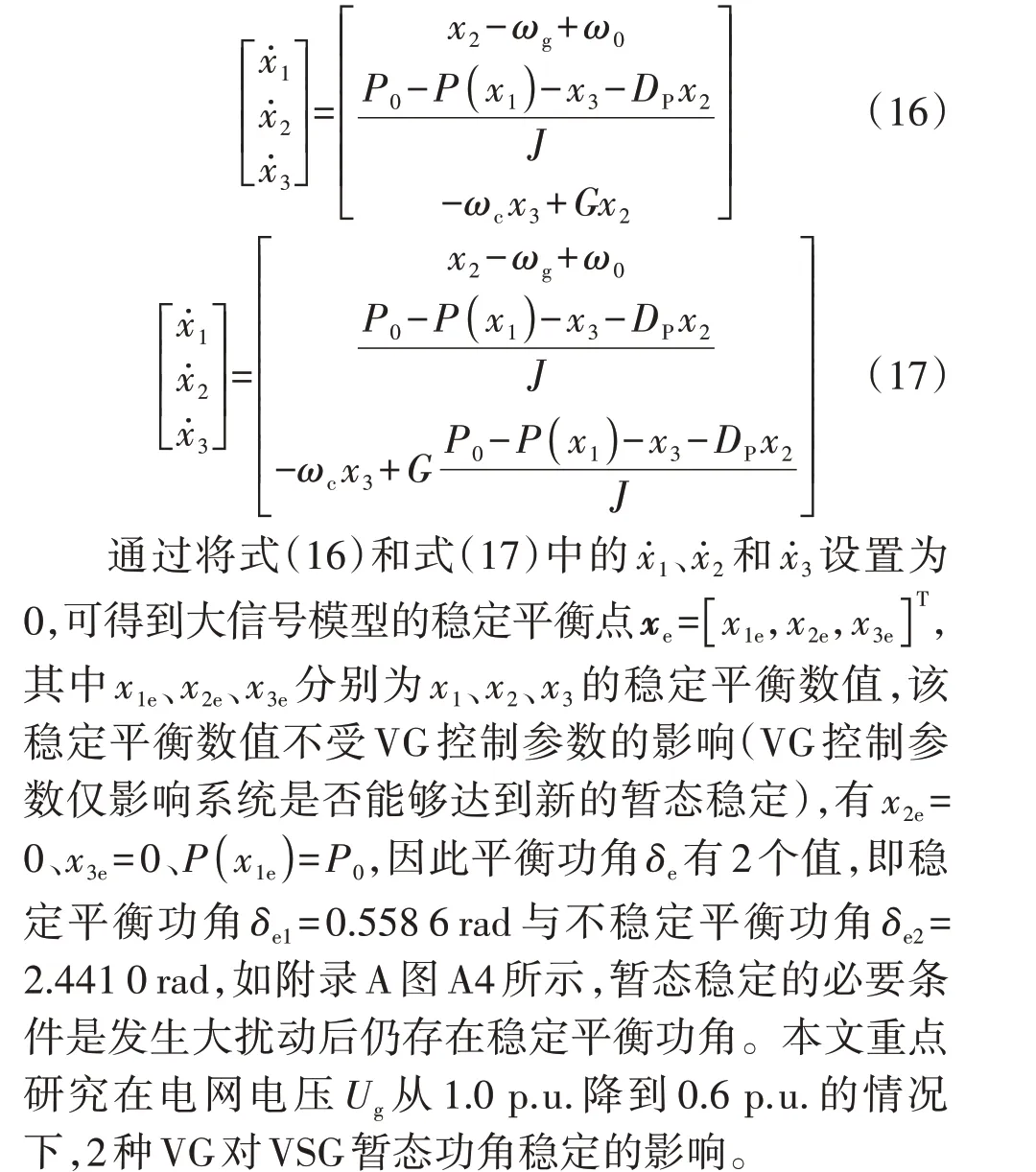
2 考虑不同调速器时的VSG 暂态功角稳定机理
本节采用EEAC 分别对LPF-VG-VSG 和HPFVG-VSG的暂态功角稳定进行机理分析。
2.1 LPF型VG对VSG暂态功角稳定的影响
由于本文主要考虑不同VG 环节对VSG 暂态稳定的影响,根据附录A 图A3 可知,LPF-VG-VSG 和HPF-VG-VSG 的动态特性均由增益G和截止频率ωc(J和DP不是本文的研究重点,相关分析见文献[7⁃8])决定。由于LPF-VG-VSG 和HPF-VG-VSG 等效电路模型与同步发电机的转子运动回路类似,考虑到DP的存在,EEAC 更适用于对系统暂态功角稳定的定性分析,可避免等面积定则(EAC)因未考虑阻尼而造成的判断极度保守的问题[8]。
根据式(7),令等值有功功率参考值Pn=P0-[G/(s+ωc)+DP]sδ,则LPF-VG-VSG 有功控制表达式为:

系统稳定性判据一般应满足:
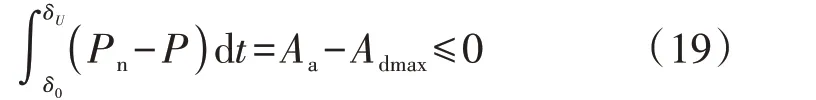
式中:δ0为正常运行情况下的功角;δU为故障下的不稳定功角;Aa为加速面积;Admax为最大减速面积。
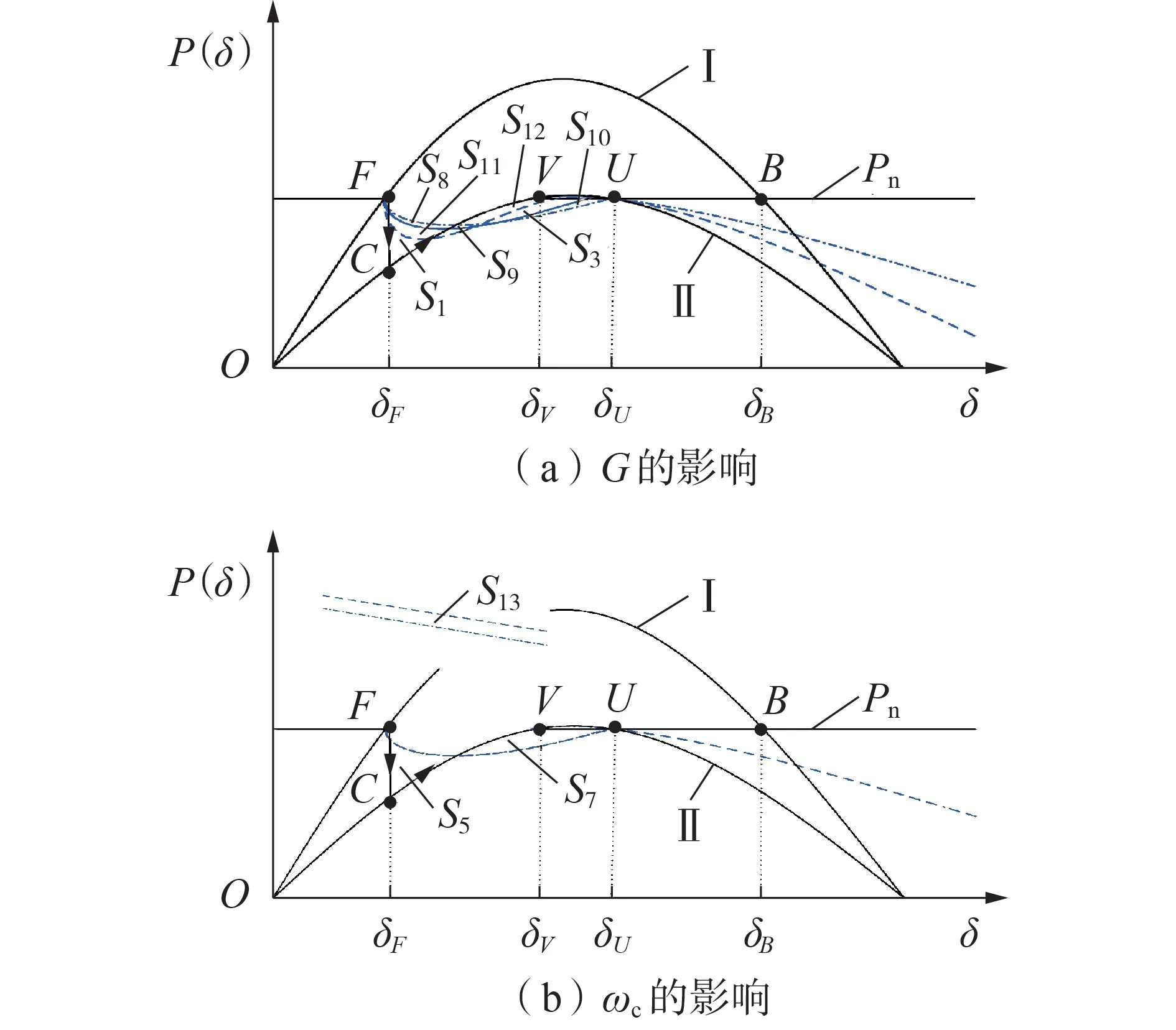
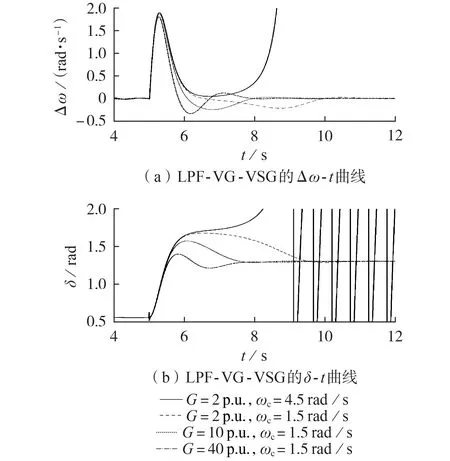
在电网电压Ug从1.0 p.u.降到0.6 p.u.的情况下,LPF-VG-VSG 功角曲线如图2 所示。图中:曲线Ⅰ为故障前的功角曲线,曲线Ⅱ为故障时的功角曲线;δF、δV、δB分别为点F、V、B处的δ值;S均表示相应区域面积。由图可知,在故障发生时,运行点从点F跳变到点C,此时P 图2 LPF-VG-VSG功角曲线Fig.2 Power angle curves of LPF-VG-VSG 当G=G0(G0=0)时,Aa=S1,Admax=S3,Aa≥Admax,造成暂态过程功角超过δU,系统最终失去暂态稳定性,如图2(a)中虚线所示,此时Admax与Aa非常接近;当G>G0时,Aa=S1-S2,Admax=S3+S4,Aa HPF-VG-VSG 功角曲线如图3 所示。当G=G0时,与2.1 节分析相同,如图3(a)中点划线所示;当G0 图3 HPF-VG-VSG功角曲线Fig.3 Power angle curves of HPF-VG-VSG 上文的机理分析分别得到了2 种VG 对VSG 暂态功角稳定的影响规律,本节基于该规律进一步量化研究关键控制参数对VSG 暂态功角稳定的影响。采用相图分析方法,通过δ-Δω平面图对比研究不同控制参数(VG 增益和截止频率)对LPF-VG-VSG和HPF-VG-VSG暂态功角稳定的影响。 为了研究不同VG 增益G对暂态功角稳定的影响,本文使用附录A 表A1 中的参数(参数G除外),分别利用式(16)和式(17)绘制δ-Δω平面图,如图4所示,可以直观地观察电压降落等大扰动下的动态响应。当δ̇>0 时,δ增大;当δ̇<0 时,δ减少。如果δ̇在不稳定平衡点U(此时对应的平衡点为V)之前降到0,则δ将收敛到新的稳定平衡点,否则将出现发散现象,导致暂态功角不稳定,如G=0(即不采用VG环节或VG 环节失效)时,虽然此时存在平衡点,但仍可能导致暂态失稳。 图4 当电网电压降到0.6 p.u.时不同增益G下的δ-Δω曲线Fig.4 δ-Δω curves under different values of gain G when grid voltage drops to 0.6 p.u. 当增益G=2 p.u.时,HPF-VG-VSG 中δ超过不稳定平衡点U处的值,出现了失稳现象,而LPF-VG-VSG能保证暂态功角稳定,稳定平衡点为(1.3025 rad,0)。本文将功角超调表示为σδi_x=(δmi-δe)/δe(i=1,2,3,4;x=L,H),其中δmi为对应的最大功角,将角频率差最大值表示为max Δωi_x=Δωmi-Δωe(i=1,2,3,4;x=L,H),其中Δωmi和Δωe分别为对应的暂态角频率最大偏差和稳态角频率偏差,Δωe= 0。对于LPFVG-VSG,σδ4_L=(1.664 3-1.302 5)/1.302 5≈27.78%,max Δω4_L=1.91 rad/s。当增益G=10 p.u.时,LPFVG-VSG、HPF-VG-VSG 均能保证系统暂态稳定,但动态特性不同,对于LPF-VG-VSG,max Δω3_L=1.868 6 rad/s,σδ3_L≈20.67%,而对于HPF-VG-VSG,σδ3_H≈24.58%,max Δω3_H=1.738 0 rad/s,稳定平衡点均与增益G=2 p.u. 时的相同。此时LPF-VG-VSG具有最低的超调特性,展现出更大的暂态功角稳定裕度,同时与HPF-VG-VSG 具有相似的角频率差最大值,因此,在这种情况下,LPF-VG-VSG 在暂态稳定性方面具有优势。当增益G=30 p.u.,发生电网电压降落时,LPF-VG-VSG、HPF-VG-VSG 的稳定平衡点与上述情况相同。LPF-VG-VSG 具有较小的功角超调,σδ2_L≈11.07%,而HPF-VG-VSG 具有更大的功角超调,σδ2_H≈25.76%,因此,LPF-VG-VSG在暂态功角稳定裕度方面优于HPF-VG-VSG。当增益G=40 p.u.时,HPF-VG-VSG 出现暂态失稳,而LPF-VGVSG仍然可稳定到稳定平衡点,此时LPF-VG-VSG的功角超调σδ1_L≈7.49%,角频率差最大值max Δω1_L=1.786 rad/s。总体而言,LPF-VG-VSG 的暂态功角稳定优于HPF-VG-VSG。 由图4(a)可知,随着增益G的增大,LPF-VGVSG 的功角超调和角频率差最大值减小,暂态功角稳定裕度增大,系统暂态稳定性加强。由附录A 图A5(a)知,增益G对HPF-VG-VSG 的量化影响过程具体分为4个阶段。第一阶段中G在[1,2]p.u.区间内增加,由于运行点超过不稳定平衡点,此时系统一直失稳,如图A5(b)所示;第二阶段中G在[3,20]p.u.区间内增加,系统维持暂态功角稳定,且其功角超调和角频率差最大值明显减小,如图A5(c)所示;第三阶段中G在[21,35]p.u.区间内增加,此时系统仍可维持暂态功角稳定,且角频率差最大值仍然减小,但功角超调反向增加,系统暂态功角稳定不断减弱,如图A5(d)所示;第四阶段中G在[36,50]p.u.区间内增加,由于运行点再次超过不稳定平衡点,此时系统失稳,临界值G1=36 p.u.,如附录A图A5(e)所示。不同增益G对VSG 暂态功角稳定的影响如附录A 表A2 所示。由表可知,G增大有利于LPF-VG-VSG 的暂态功角稳定,但容易导致HPF-VG-VSG失稳。 不同截止频率ωc也会对VSG 暂态功角稳定产生影响。本文使用附录A表A1中的参数(参数ωc除外),分别利用式(16)和式(17)绘制δ-Δω平面图,如图5所示。由图可知:随着ωc增大,系统暂态功角稳定裕度减小,甚至出现失稳现象;随着ωc增大,系统轨迹向右移动,功角超调量变大,不利于暂态功角稳定,并在ωc达到4.5 rad/s 时出现功角失稳,虽然在ωc增大时LPF-VG-VSG、HPF-VG-VSG 具有共性,但是其动态特性仍然不同。 图5 当电网电压降到0.6 p.u.时不同截止频率ωc下的δ-Δω曲线Fig.5 δ-Δω curves under different values of cutoff frequency ωc when grid voltage drops to 0.6 p.u. 当ωc=0.5 rad/s 时,LPF-VG-VSG 和HPF-VGVSG 均暂态功角稳定但存在差异,对于LPF-VGVSG,σδ1_L≈26.60%,max Δω1_L=1.915 rad/s,而对于HPF-VG-VSG,σδ1_H≈26.68%,max Δω1_H=1.868 rad/s,在这种情况下,LPF-VG-VSG 的暂态功角稳定更优。当ωc=1.5 rad/s 时,HPF-VG-VSG 失去稳定性,而LPF-VG-VSG 仍然维持暂态稳定,此时LPF-VG-VSG的σδ2_L增加到28.980%,而max Δω2_L几乎不变。当ωc=4.5 rad/s 时,LPF-VG-VSG 和HPF-VG-VSG 均失去暂态功角稳定。 不同截止频率ωc下系统暂态功角稳定的比较如附录A 表A3 所示。由表可知,随着ωc增加,LPFVG-VSG和HPF-VG-VSG的暂态功角稳定均下降,且HPF-VG-VSG最先失稳。 通过3.1 节和3.2 节的分析可知,增益G和截止频率ωc的合理设置对提高系统暂态功角稳定具有重要意义。为了量化VG 控制参数对LPF-VG-VSG和HPF-VG-VSG 暂态功角稳定的整体影响,本文综合考虑准确性和计算机计算负担,将G和ωc的计算步长分别设置为1 p.u.和0.05 rad/s,对于每个指定的截止频率ωc,利用附录B 图B1 所示流程得到系统暂态功角稳定下的增益G,重复该流程可得到当电网电压降到0.6 p.u.时,在G和ωc共同作用下系统暂态功角稳定的整体影响区域,如附录B 图B2 所示,图中蓝色区域为暂态功角稳定区域,白色区域为暂态功角不稳定区域。 由图B2(a)知,对于LPF-VG-VSG:当ωc<1.2 rad/s时,无论G在(0,+∞)区间内取何值,均能保持系统暂态功角稳定,此时系统暂态稳定裕度最大;当ωc在[1.2,3.4]rad/s 区间内取值时,若G≥2 p.u.,则系统暂态功角稳定,否则将出现暂态失稳,可见系统暂态稳定裕度减小;当ωc>3.4 rad/s 时,G超过3 p.u.才能保证系统暂态功角稳定,此时系统暂态稳定裕度最小。由图B2(b)可知,对于HPF-VG-VSG:只有当ωc≤2.1 rad/s 时,才有可能保持系统暂态功角稳定,否则无论G在(0,+∞)区间内取何值,系统均会失稳;随着ωc取值减小,系统维持暂态功角稳定的G取值范围增大,此时系统暂态稳定裕度增大,如在ωc≤0.5 rad/s 时,G可在[1 p.u.,+∞)区间内取任何值,此时系统暂态功角稳定裕度最大。综上可知,在VG 控制参数的联合影响下,LPF-VG-VSG 的暂态功角稳定区域面积(暂态功角稳定裕度)明显比HPFVG-VSG 的大,因此在相同的控制参数条件下,在维持系统暂态功角稳定方面,LPF-VG-VSG 比HPFVG-VSG更有优势。 根据前面的结论,可以总结出VG 的设计指导原则如下。 首先,在控制参数相同的情况下,工程技术人员应当优先选择LPF 型VG,其在维持系统暂态功角稳定方面具有较大的稳定裕度。 然后,为了使得LPF型VG具有更好的系统暂态功角稳定,根据附录B 图B2(a),应当优先选择较小的截止频率,同时增益具有较大的选择自由度,此时系统暂态稳定裕度最大,不易失稳。如在采用附录A 表A1 的系统参数(除增益G和截止频率ωc外)时,为了获得最大的稳定裕度,LPF 型VG 的截止频率取值小于1.2 rad/s。 最后,对于某些负荷波动剧烈的地区,出于快速恢复频率稳定的需要,往往采用HPF 型VG,根据附录B 图B2(b),应当选择较小的截止频率,以维持故障时的系统暂态功角稳定,但是此时增益并无LPF型VG 中增益所具有的较大的选择自由度,而是只能在一个区间范围内进行选择。如在采用附录A 表A1的系统参数(除增益G和截止频率ωc外)时,为了获得相对较大的稳定裕度,HPF型VG的截止频率可选取1.5 rad/s,增益选择的区间范围为[3,35]p.u.,根据附录A表A2,增益可优先选取20 p.u.。 为了验证理论分析的正确性,在MATLAB/Simulink 中建立图1(a)所示的仿真模型,系统参数如附录A表A1所示。运行工况为:t=5 s时电网发生三相接地短路故障,假设此时电网电压Ug降至额定电压的60%。为了对比LPF-VG-VSG 和HPF-VGVSG 的暂态功角稳定,对不同控制参数下的系统暂态功角稳定进行仿真分析,不同控制参数的设置如表1 所示,表中G为标幺值。仿真结果如附录C 图C1—C5所示。 表1 5种情况下的控制参数设置Table 1 Control parameter setting for five cases 控制参数ωc变化下HPF-VG-VSG 和LPF-VGVSG 暂态功角稳定的仿真实验控制参数设置如表1中的情况1、4、5 所示,仿真结果如附录C 图C1、C4、C5 所示。情况4 下,此时ωc在[0.5,1.1]rad/s 区间内,当电网电压降到0.6 p.u.时,HPF-VG-VSG 和LPF-VG-VSG 均可保证系统暂态功角稳定,此时HPF和LPF型VG下的max Δω分别为1.738 rad/s和1.915 rad/s,maxδ分别为1.622 7 rad 和1.649 0 rad,均非常接近,但是HPF-VG-VSG 的系统短时振荡时间较长,因而造成系统保持稳定的时间延后,这说明HPF-VG-VSG 在保证暂态稳定性方面不如LPF-VGVSG。情况1下,此时ωc在[1.2,3.4]rad/s区间内,当电网电压降到0.6 p.u.时,出现了不同的暂态响应,HPF-VG-VSG 的系统失稳,而LPF-VG-VSG 系统暂态功角稳定,且maxδ和max Δω分别为1.6643 rad和1.910 rad/s,更加体现了LPF-VG-VSG 在维持系统暂态功角稳定方面的优势。情况5 下,ωc在(3.5 rad/s,+∞)区间内,此时LPF-VG-VSG 的系统才失去暂态功角稳定,而HPF-VG-VSG 的系统早已失稳。与第2节和第3节的分析一致,在不同参数ωc下,LPF-VG-VSG比HPF-VG-VSG在维持系统暂态功角稳定方面具有优势。 对不同控制参数G下HPF-VG-VSG 以及LPFVG-VSG 的暂态功角稳定进行仿真分析,分别采用情况1—3 的控制参数进行对比,仿真结果如附录C图C1—C3 所示。情况1 下,G在[1,2]p.u.区间内,与上文ωc在[1.2,3.4]rad/s 区间内的分析相同。情况2 下,G在[3,20]p.u.区间内,当电网电压降到0.6 p.u.时,HPF-VG-VSG和LPF-VG-VSG均可维持系统暂态稳定,同时HPF 型VG 和LPF 型VG 下max Δω分别为1.738 0 rad/s 和1.868 6 rad/s,maxδ分别为1.622 7 rad 和1.571 7 rad,均非常接近,但HPF-VGVSG 系统短时振荡时间较长,造成系统保持稳定的时间延后,这说明LPF-VG-VSG 在保证暂态稳定性方面比HPF-VG-VSG 具有明显优势。情况3下,G在[36 p.u.,+∞)区间内,当电网电压降到0.6 p.u.时,LPF-VG-VSG和HPF-VG-VSG出现不同的暂态行为,LPF-VG-VSG 的系统仍可保证趋于暂态功角稳定,但HPF-VG-VSG 的系统则出现失稳。遵循Δω和δ随G增大而减小的规律,LPF-VG-VSG 中max Δω和maxδ分别为1.786 0 rad/s 和1.400 1 rad,同时系统在出现了小幅振荡现象后才趋于稳定。而对于HPF-VG-VSG,P、Δω、δ和电网电流Ig曲线均发生振荡,出现系统暂态失稳。与第2节和第3节的分析一致,在不同参数G下,LPF-VG-VSG 比HPF-VG-VSG在维持系统暂态功角稳定方面的效果更好。 通过以上分析可以得出:在维持系统暂态功角稳定方面,相同控制参数条件下LPF-VG-VSG 比HPF-VG-VSG 更具有优势,同时,不同控制参数的选择对LPF-VG-VSG 维持暂态功角稳定起着关键作用。当电网电压降落到0.6 p.u.时不同控制参数下的仿真结果如图6所示。 图6 当电网电压降到0.6 p.u.时不同控制参数下的仿真结果Fig.6 Simulative results under different control parameters when grid voltage drops to 0.6 p.u. 由图6 可知,当ωc=1.5 rad/s 时,随着G的不断增大,LPF-VG-VSG 的系统暂态功角稳定得到增强,功角过冲和角频率偏差明显减小,暂态功角稳定裕度不断增大,有利于维持系统暂态功角稳定,与第2节和第3 节的分析一致,同时振荡衰减明显减弱,且均能最终达到相同的稳定状态,这说明暂态过程中通过VG 仅增加了暂态阻尼,不会改变系统的稳定平衡点。当G=2 p.u.、ωc=1.5 rad/s 时,系统可保持暂态功角稳定。当G=2 p.u.、ωc=4.5 rad/s 时,LPFVG-VSG 的系统暂态功角出现持续振荡现象,说明系统发生了暂态功角失稳。仿真结果与理论分析结果一致,验证了本文理论分析的正确性。 本文以不同VG 的VSG 为研究对象,构建不同VG 的大信号暂态模型,揭示不同VG 的VSG 暂态功角稳定影响机理,并进行仿真验证,得到以下结论。 1)VG 控制参数对维持系统暂态功角稳定起着至关重要的作用。对于LPF-VG-VSG,VG 增益的增加或截止频率的减小均能增强系统暂态功角稳定;而对于HPF-VG-VSG,VG 增益的增加将造成系统暂态功角稳定先增强后减弱,而截止频率的减少会增强系统暂态功角稳定。 2)LPF-VG-VSG 的暂态功角稳定较HPF-VGVSG 更出色,当2 种VG 取相同的增益和截止频率时,LPF-VG-VSG 的暂态功角稳定裕度远大于HPFVG-VSG。 3)LPF-VG-VSG 的暂态功角稳定裕度随着调速器增益G的增加而增大,随着调速器截止频率ωc的增大而减小。而HPF-VG-VSG 的暂态功角稳定裕度随着G和ωc的增加大多呈现下降趋势,容易出现暂态功角失稳。 4)本文提出的VG 具体设计指导原则,可为今后含VG的变换器暂态稳定性提升提供理论指导。 5)本文中VG 对VSG 暂态功角稳定影响的机理,是在假定转子控制回路、无功控制回路、限流控制回路等其他控制回路不影响VSG 暂态功角稳定的前提下得出的,后续笔者将继续研究包括VG 在内的多个控制回路共同作用对VSG 暂态功角稳定的影响。 附录见本刊网络版(http://www.epae.cn)。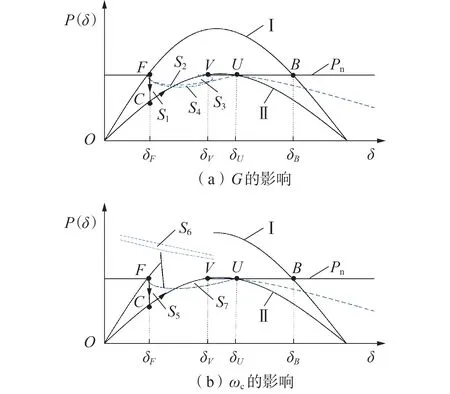
2.2 HPF型VG对VSG暂态功角稳定的影响
3 VG 控制参数对VSG 暂态功角稳定影响程度量化研究
3.1 VG增益G对VSG暂态功角稳定的影响

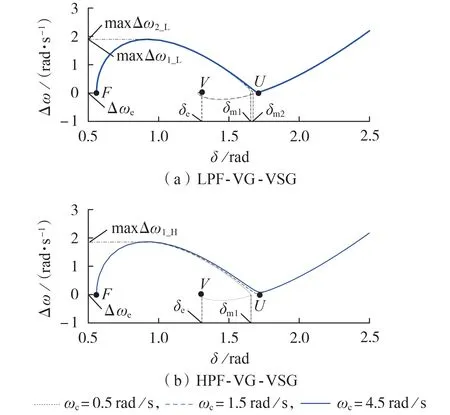
3.2 VG截止频率ωc对VSG暂态功角稳定的影响
3.3 VG控制参数对VSG暂态功角稳定的整体影响
3.4 VG整体设计指导原则
4 仿真验证与分析

5 结论

