构网型变流器对交流系统低频振荡的影响分析与阻尼控制

薛翼程，张哲任，徐 政，黄 莹

（浙江大学电气工程学院,浙江省杭州市 310027）

0 引言

新型电力系统的主要特征之一是大规模新能源通过电力电子变流器接入电网［1］。与同步机不同,变流器通过控制环与交流系统实现同步,灵活性较强,但其控制的复杂性和多时间尺度特性给新型电力系统的稳定性分析带来挑战［2-3］。模块化多电平变流器（modular multilevel converter,MMC）功率因数可控,谐波含量低,在柔性直流输电系统中应用广泛［4］。然而,当MMC 与同步机容量接近时,其控制环可能影响系统的机电振荡模态,危害系统安全稳定运行［5］。

传统电力系统中,同步机构建并支撑系统电压,以维持电力系统的正常运行。电压源变流器（voltage source converter,VSC）通常采用跟网型控制策略,其通过锁相环（phase-locked loop,PLL）与电网同步,本质上属于受控电流源［6］。然而,在新型电力系统中,跟网型VSC 由于不具备电压构建能力而难以在弱电网下稳定运行,此时需要构网型VSC承担自主构建电压的任务［7-8］。近年来,国内外学者对构网型VSC 和同步机的特性对比开展了广泛研究,其中最典型的构网型控制是虚拟同步机（virtual synchronous generator,VSG）。VSG 能够模拟同步机的转子运动、调频、调压等特性,与同步机的外特性相似。然而,VSG 和同步机的控制实现方式不同。同步机之间通过转子的机械摇摆特性完成同步,由励磁系统完成电压控制。而VSG 由控制器实现上述功能。因此,以VSG 为代表的构网型VSC的低频阻尼特性研究需要计及控制方式。有功控制方面,文献［9］对比了VSG 和下垂控制的阻尼特性,指出VSG 的输出有功功率振荡特性强于下垂控制；文献［10］研究了转子模拟回路控制参数对双馈风电机组低频阻尼的影响。电压控制方面,文献［11］分析了双闭环控制中电压控制器对VSG 的附加阻尼效应；文献［12］借鉴了电力系统稳定器（power system stabilizer,PSS）的思想,在VSG 的电压环中增加了正比于频率偏差的阻尼电压分量以抑制振荡；文献［13］指出附加虚拟阻抗能够起到同步机阻尼绕组的作用,以提升VSG 的阻尼特性；文献［14］提出了虚拟阻抗和虚拟PSS 结合的VSG 阻尼补偿方式。控制架构方面,文献［15］指出构网型/跟网型混合型直驱风电场弱电网下的并网稳定性强于单一跟网型直驱风电场；文献［16］采用模态分析法对比了VSG 和跟网型变流器的低频振荡特性。然而,上述文献关注构网型变流器自身的振荡特性,未考虑变流器与同步机的耦合特性。

低频振荡常发生在涉及多同步机相互作用的交流互联系统中,因此在构网型变流器低频阻尼研究中需要考虑同步机的特性。文献［17］建立了含VSG 互联系统的状态空间模型,研究了原动机调频环节对系统低频振荡的影响；文献［18］研究了计及直流电压动态的VSG 型多端柔性直流对系统阻尼的影响；文献［19］对比分析了跟网型和功率同步控制型MMC 对同步机阻尼的影响机理。然而,上述文献仅考虑了单一类型的构网型控制,并未讨论不同控制结构的构网型变流器对交流系统阻尼的影响,并且该问题在现有研究中仍未得到充分解决。

综上,目前构网型变流器对交流系统低频振荡影响的研究仍存在一定局限。现有文献提出的分析方法大多针对特定类型的构网型控制策略,难以扩展应用于分析多种构网型变流器的阻尼特性。因此,适用于构网型变流器对交流系统低频振荡机理研究的通用建模、分析和阻尼控制方法仍有待完善。

针对现有研究的不足,本文计及同步机和构网型MMC 的耦合特性,建立了系统阻尼转矩分析模型,并提出了衡量系统阻尼特性的判据。在此基础上,对比分析了3 种构网型控制:VSG、下垂控制和幅相控制对系统阻尼转矩的影响机理。针对不同控制策略,提出了增强系统阻尼的构网型MMC 的控制回路改造方案。

1 阻尼转矩分析建模

1.1 系统模型

用于本文研究的同步机并联构网型MMC 供电系统拓扑结构如图1 所示。图中:Z1、Z2和Z3表示3条输电线路阻抗；XT,SG、XT,v分别表示同步机和MMC 的联结变压器漏抗；iSG、iv分别表示同步机和MMC 的注入电流；uSG、uv分别表示同步机和MMC的公共连接点（point of common coupling,PCC）的交流母线电压；PSG、QSG和Pv、Qv分别表示同步机与MMC 的有功、无功功率；uIB=1.0 p.u.为受端电网母线电压；Udc为构网型MMC 的直流电压,通常由其他变流器控制［7］。

图1 系统拓扑结构Fig.1 System topology

本文关注的3 种构网型控制结构框图如附录A图A1 所示。图中:VSG 和下垂控制均采用电压-电流双闭环控制。VSG 模拟同步机的转子运动方程,其惯性常数和阻尼系数分别为Jv、Dv；而下垂控制的有功控制无惯性响应特性,其有功-频率下垂系数为KPω。二者的电压环中具备无功-电压下垂控制,通过下垂系数KQV生成偏差量ΔU调节PCC 电压参考值Uvref。幅相控制通过单层控制环控制Pv、Qv并直接生成MMC 的内电势幅值Ucv和相位θv,也称为间接电流控制［1］或直接功率控制［20-21］。

下文中含abc 或dq（xy）下标的变量分别表示相应物理量在abc 静止坐标系或dq（xy）旋转坐标系下的分量,含下标ref 的变量表示相应物理量的参考值,Δ 表示各物理量的增量,下标0 表示稳态工作点处的值,s为微分算子,各量为标幺值。

1.2 同步机数学模型

研究系统阻尼特性时,需要在稳态工作点处对系统的微分-代数方程组线性化。同步机转子运动方程为:

式中:JSG为同步机的惯性时间常数；ωSG、δSG分别表示同步机的角频率和功角；ω0为额定角频率（有名值）；Pm表示同步机的机械转矩分别表示同步机的d、q轴次暂态电动势；同步机6 阶主电路及励磁系统模型如附录A 式（A1）—式（A2）所示；系数K1、K2的表达式详见式（A3）；同步机端口电气量的坐标变换关系如式（A4）和式（A5）所示。

1.3 构网型MMC 数学模型

在MMC 的dq坐标系下,VSG 和下垂控制的有功控制环为:

式中:Gω（s）为有功-频率传递函数；ωv表示MMC 的虚拟转子角频率；θ为MMC 的功角。

对 于VSG,Gω（s）=1/（Jvs+Dv）；对 于 下 垂 控制,Gω（s）=KPω。考 虑 无 功-电 压 下 垂 的 电 压 控 制环为:

式中:ivdref、ivqref分别为内环d、q轴电流指令值；GU（s）为电压环传递函数；U0为空载电压设定值；KU、TU分别为电压环比例-积分（PI）控制器比例、积分系数。

输出电流控制和环流抑制控制为:

式中:md、mq和md2、mq2分别为调制信号的d、q轴分量和二倍频d、q轴分量；GI（s）、Gccsc（s）分别为输出电流环和环流抑制控制的传递函数；idiffd2、idiffq2分别为MMC 桥 臂 环 流 的 二 倍 频d、q轴 分 量；Xv、Xarm分别为MMC 的等效内电抗和桥臂电抗；KI、TI和Kccsc、Tccsc分别为内环电流控制和环流抑制控制的PI 控制器比例、积分系数。

对于幅相控制的MMC,其有功-相位控制和无功-电压控制环为:

式中:Gp（s）、Gq（s）分别为有功-相位控制和无功-电压控制的传递函数；Kp、Tp和Kq、Tq分别为 有功、无功环的PI 控制器比例、积分系数。

锁相环监测PCC 电压的相位,其动态特性如式（7）所示。其中,Gpll（s）为锁相环传递函数；Kpll、Tpll分别为锁相环PI 控制器的比例、积分系数。

MMC 的主电路采用计及二倍频分量的10 阶模型［22］,其模型说明如附录B 式（B1）—式（B4）所示。对上述方程线性化,能够得到在构网型MMC 电气量、控制量之间的传递函数。MMC 端口电气量的坐标变换关系见附录A 式（A4）和式（A5）。

1.4 交流电网数学模型

同步机和MMC 通过交流电网产生耦合。xy坐标系下,交流电网方程如附录A 式（A6）和式（A7）所示。在xy坐标系下,描述MMC 动态特性的传递函数矩阵可以视为导纳矩阵Ymmc（s）。因此,计及MMC 影响的同步机端口阻抗矩阵ZSG（s）为:

式中:ZSG（s）的具体表达式如附录A 式（A8）所示；Rx（s）、Ry（s）和Xx（s）、Xy（s）分别定义为同步机的x、y轴端口电阻和电抗。

系统的阻尼转矩分析模型如图2 所示,其中,USGref表示同步机端电压参考值。同时,含下标dq或xy的变量代表相应坐标系下的矢量,例如uvdq=uvd+juvq,j 为虚数单位。

图2 阻尼转矩分析模型Fig.2 Damping torque analysis model

式中:MT（s）为复转矩系数,|MT（s）|和φT分别为其幅值和相位；ΔTs、ΔTd分别为同步转矩和阻尼转矩分量。ΔTd能够衡量系统的阻尼水平。当φT<0 时,系统阻尼转矩为负,有低频振荡失步的风险［19］。

2 构网型变流器的低频振荡影响机理分析

2.1 同步机端口阻抗对阻尼转矩的影响机理

在含构网型MMC 的交流系统中,ZSG（s）各分量均受到MMC 动态的影响。因此,首先分析ZSG（s）各分量对ΔTd的影响。为了获得直观的解析表达式,在图2 的基础上建立一个简化模型,其不考虑同步机转子阻尼绕组和励磁系统的阻尼作用,此时有:

ΔPSG与ΔδSG之间的简化复转矩系数MTs（s）为:

式中:MX1（s）、MX2（s）分别为Xx（s）、Xy（s）的复转矩系数；MR（s）为电阻分量Rx（s）+Ry（s）的复转矩系数；系数a0表示与ΔδSG同相位的转矩分量,其不影响与ΔωSG同相位的转矩分量。

定义MX（s）=MX1（s）+MX2（s）为电抗分量的复转矩系数,式（11）中各分量表达式为:

式中:系数kd2、kq2以及a0至a4的表达式详见附录A式（A9）。

选取主导振荡频率fd的范围0.1 Hz≤fd≤10 Hz,对同步机端口阻抗矩阵开展灵敏度分析,上述简化模型中端口阻抗矩阵各分量的复转矩系数以及详细模型中MT（s）的幅值、相位如图3 所示,其中,系统参数如附录C 表C1 所示。图3 表明,忽略上述阻尼作用会导致MTs（s）和MT（s）的幅值、相位在数值上有差异,但二者变化趋势一致,因此简化模型能够反映ZSG（s）各分量对复转矩系数的影响。

α1(t)=α2(t)=0.55+0.05cos(2 t)，令通过计算可知该系统满足定理3.3和定理4.1的条件，则该系统是持久的，并且存在唯一的正的一致渐近稳定的概周期解.

图3 端口阻抗矩阵灵敏度分析Fig.3 Sensitivity analysis of terminal impedance matrix

图3（a）和（b）表明,各电抗分量的复转矩系数MX1（s）、MX2（s）、MX（s）与MT（s）变化趋势基本保持一致。而式（12）表明,电阻分量的复转矩系数同时受ZSG（s）中电阻、电抗分量的影响。结合图3（a）和（c）,MR（s）的幅值明显小于MX（s）,并且其相位与MT（s）的相位范围不同。图3（d）表明随着fd的变化,MR（s）的相位在180°附近,且变化趋势与MT（s）差异明显,说明电阻分量对MT（s）的影响较小。

因此,构网型MMC 接入系统后,其主要通过改变同步机端口阻抗矩阵中电抗分量的复转矩系数影响系统阻尼。当其负阻尼分量抵消同步机固有阻尼时,易引起系统低频振荡。

2.2 电流环阻尼特性分析

结合图1 所示系统模型,研究构网型MMC 各层控制器对系统阻尼的影响。在后文中,将采用图2 所示模型开展阻尼特性分析。首先,以VSG 为例,分析采用双闭环控制的构网型MMC 电流控制器的阻尼特性。改变GI（s）的积分常数TI,MT（s）的幅频、相频特性曲线如图4（a）所示。此时GU（s）参数KU=2、TU=0.08。根据式（9）,当fd处|MT（s）|增大,且φT滞后程度越大,表明ΔTd越小,系统在fd附近越容易低频振荡。根据图4（a）,在幅频特性曲线峰值频率fmag附近,相频特性曲线出现由正变负的跃变,且最大滞后相位对应的频率略大于fmag,因此系统阻尼特性的判据为|MT（s）|的变化趋势和φT的滞后程度。图4（a）显示,当MMC 的内环电流控制器参数TI由0.01 增大至0.1 时,电流环的带宽fbcc的变化在正常范围内,为40 Hz≤fbcc≤280 Hz,而|MT（s）|和φT的变化不明显。因此,VSG 的内环电流控制器对系统低频振荡的影响较小,主要原因是电流环带宽与低频段有数量级差异。改变Gccsc（s）的积分常数Tccsc,MT（s）的幅频、相频特性曲线如图4（b）所示。理论分析结果表明,相比内环电流控制,环流抑制控制对系统阻尼的影响更小,其主要原因是MMC 环流的二倍频分量对输出电流影响很小,因此对ZSG(s)的影响较小。因此,图4（a）和（b）证明了MMC 的输出电流、环流抑制控制均不会导致系统在低频段出现负阻尼。

图4 VSG 电流和电压控制环阻尼特性分析Fig.4 Damping characteristic analysis of current and voltage control of VSG

2.3 VSG/下垂控制阻尼特性分析

2.3.1 含无功-电压下垂控制的电压环阻尼特性分析

为了研究VSG 电压控制器的阻尼特性,首先保持KQV=0,改变GU（s）的积分常数TU,MT（s）的幅频、相频特性曲线如图4（c）所示。当TU=0.01 时,由于fd>3 Hz,系统不易发生低频振荡。而当TU从0.05 增大至0.15 时,fd逐渐减小并小于3 Hz,系统有低频振荡风险。在这个过程中,φT滞后程度减小且|MT（s）|峰值减小,表明系统阻尼增强,但仍存在负阻尼频段。因此,VSG 的电压控制环不仅会影响系统阻尼,还会影响fd,因此其动态特性可能导致系统出现负阻尼,增加低频振荡风险。

保持TU=0.08,改变KQV,使其从0 增大至0.2,MT（s）的幅频、相频特性曲线如图4（d）所示。计算结果表明,随着KQV增大,φT滞后程度减小且|MT（s）|峰值减小,表明系统阻尼特性改善。低频段fd略微增大,但变化不明显。因此,采用无功-电压下垂控制能够改善由VSG 电压控制引起的负阻尼作用。

2.1 节 证 明,MT（s）主 要 受ZSG（s）中 电 抗 分 量MX（s）的影响,因此研究VSG 电压控制对MX（s）的幅频、相频特性曲线的影响,如图5（a）和（b）所示。图5（a）和（b）表明当参数TU和KQV改变时,MX（s）的相位滞后效应是MT（s）出现负阻尼转矩分量的主导因素,并且增大KQV能够削弱相位滞后效应,提升系统阻尼。

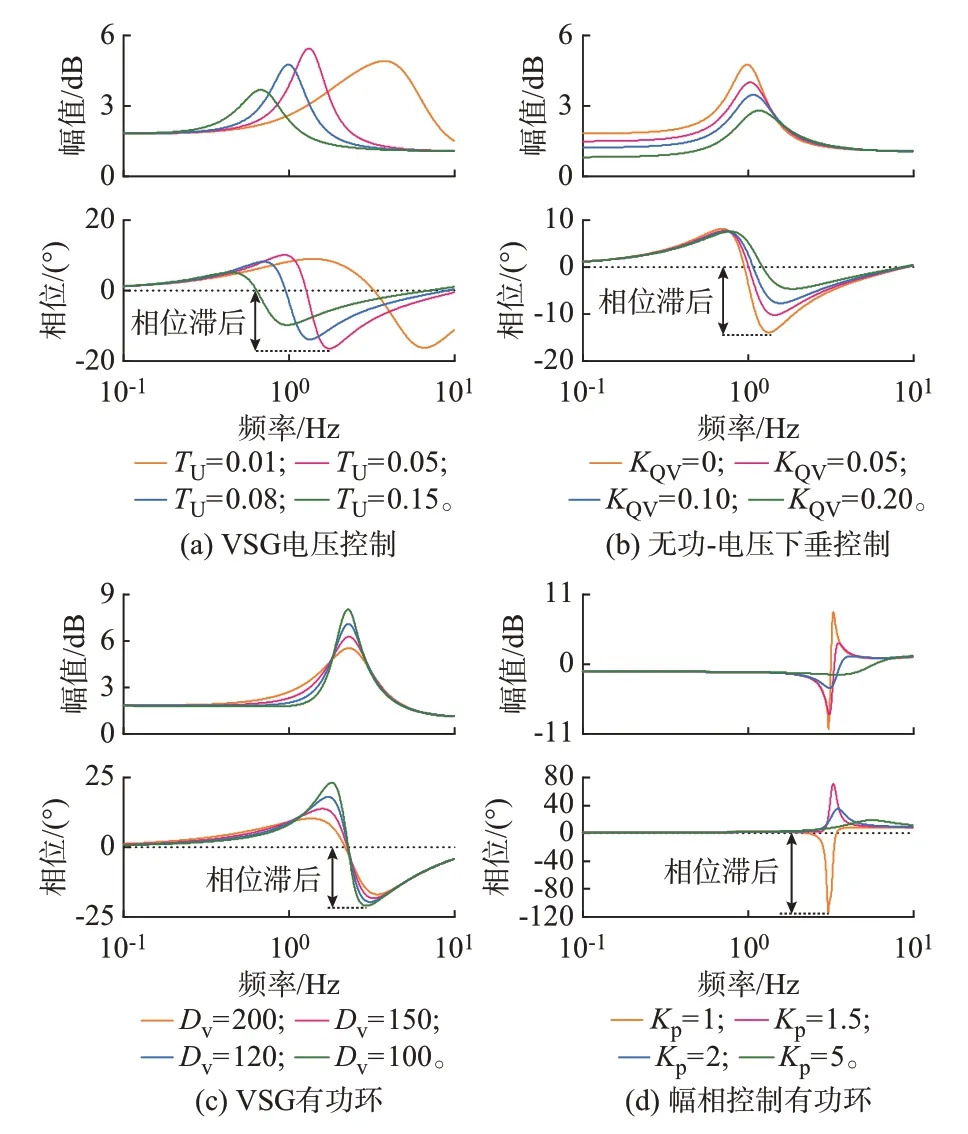
图5 电压控制和有功控制参数对MX(s)的影响Fig.5 Ettect of voltage control and active power control parameters on MX(s)

从变流器的视角出发,分析VSG 电压下垂控制的阻尼效应。由于电流控制对阻尼特性影响较小,忽略其动态特性,即认为ivdref=ivd、ivqref=ivq,MMC 的电压-电流之间的开环传递函数为:

式中:GQM（s）为无功-电压下垂控制引入的反馈支路传递函数。

以KQV=0.2 为例,GQM（s）的幅频、相频特性曲线如附录A 图A2（a）所示。图A2（a）表明,GQM（s）将在低频段为电压-电流之间的传递函数提供超前相位,该效应有利于改善系统阻尼特性。同时,根据式（13）,GQM（s）正比于KQV,因此随着KQV增大,超前相位增大,系统阻尼特性进一步提升。

2.3.2 VSG 与下垂控制有功环阻尼特性对比

下垂控制区别于VSG 的最主要特征是其有功环ΔPv与Δθ之间的传递函数为一阶。因此,下垂控制可以视为VSG 的一种特定情况［20］,即:

由于VSG 有功环中Dv对阻尼的影响明显大于Jv［19］,为 了 对 比VSG 和 下 垂 控 制 有 功 环 对 系 统 阻 尼的影响,首先,设置Jv=10 并保持TU=0.02,改变Dv,MT（s）的幅频、相频特性曲线如附录A 图A3（a）所示。当Dv减小时,低频段φT滞后程度和|MT（s）|的峰值均显著增大,说明VSG 需要足够的Dv以维持系统的正阻尼转矩。根据式（14）,减小Dv与增大KPω等效,使KPω由0.01 增大至0.1,MT（s）的幅频、相频特性曲线如图A3（b）所示。理论分析表明,Dv与KPω对 系 统 的 阻 尼 影 响 差 异 明 显,原 因 包 括:1）改变Dv几乎不影响fd,而随着KPω增大,fd增大并且可能超过3 Hz；2）随着KPω增大,虽然低频段φT和|MT（s）|的峰值均减小,但φT>0,表明系统阻尼转矩为正,低频振荡风险较小；3）虽然fd>3 Hz 时,ΔTd可能为负,但随着KPω增大,φT滞后程度和|MT（s）|的峰值均减弱,表明系统阻尼增强。因此,系统不易出现大于3 Hz 的 振 荡 模 态；4）VSG 的φT滞 后 程 度 和|MT(s)|的峰值均较大,因此阻尼转矩分量小于下垂控制。根据上述分析,虽然Dv与KPω在数学关系上具有等效性,但VSG 与下垂控制的有功环对阻尼影响并无相似性。下垂控制由于其无惯性响应的特性,很难引起振荡失稳,而VSG 的有功环动态则可能引起系统发生低频振荡。

2.4 幅相控制阻尼特性分析

2.4.1 幅相控制有功环阻尼特性分析

对于幅相控制,分别研究其有功-相位控制和无功-电压控制对系统阻尼的影响。首先,分别保持Tp=0.02,使Kp从1 增 大 至5；保 持Kp=5,使Tp从0.005 增大至0.05,MT（s）的幅频、相频特性曲线如附录A 图A4（a）所示。图A4（a）表明,当Kp减小时,低频段|MT（s）|的峰值先减小后增大,而φT滞后程度一直增大。因此,系统阻尼转矩随着Kp的减小而减弱,系统可能发生振荡失稳。Tp也会影响系统的阻尼特性。减小Tp可能减弱系统阻尼,但fd也会随之增大并超过3 Hz。因此,改变Tp不易在系统中引发低频振荡。

为了分析幅相控制有功环对系统阻尼特性的影响机理,研究参数Kp对MX（s）的幅频、相频特性曲线的影响,并与VSG 的有功环参数Dv进行对比,结果如图5（c）和（d）所示。图5（c）和（d）表明,尽管幅相控制和VSG 对MX（s）的曲线变化趋势的影响有差异,但减小Dv和Kp都会增强MX（s）的相 位 滞后效应,导致系统阻尼特性减弱。

同样地,从变流器的视角出发,分析有功-相位控制的阻尼效应。幅相控制的内电势虚拟转子角频率Δωve与ΔPv的关系为:

幅相控制与VSG 的有功环的相频响应特性为:

Gp（s）和Gω（s）的 频 率 特 性 曲 线 如 附 录A图A2（b）所示。根据图A2（b）,当Kp减小时,Gp（s）在低频段相位滞后效应增大,该特性将为系统提供负阻尼。当VSG 的阻尼系数Dv减小时,图A2（b）表明Gω（s）在低频段相位滞后效应同样增大,其特性与Gp（s）类似。因此,尽管幅相控制和VSG 的有功环结构有区别（Gp（s）为PI 控制器,而Gω（s）为一阶惯性环节）,二者对系统阻尼的影响机理具有类似之处。

2.4.2 幅相控制无功环阻尼特性分析

保持有功环参数Kp=5、Tp=0.02,分别改变Kq从0.05 增 大 至0.5、Tq从0.005 增 大 至0.2,MT（s）的幅频、相频特性曲线如附录A 图A4（b）所示。图A4（b）表明,幅相控制的参数Tq对阻尼的灵敏度高于Kq。然而,在有功环参数合适的情况下,Kq与Tq改变时φT>0,因此无功环动态特性不会引起系统出现负阻尼。该特性与VSG 有明显区别,因为VSG 的电压控制环对系统阻尼影响明显,并且可能提供负阻尼。因此,构网型MMC 的无功-电压控制环对系统阻尼的影响与控制器的结构相关。

2.4.3 锁相环阻尼特性分析

幅相控制属于基于锁相环的构网型控制策略［1］。为了研究锁相环动态特性对系统阻尼的影响,改变Kpll,使得锁相环的阻尼比σpll从0.8 增大至1.4,同时维持其带宽在20～40 Hz 内。MT（s）的幅频、相频特性曲线如附录A 图A5 所示。图A5 表明,增大锁相环的阻尼比,|MT（s）|的峰值增大,φT滞后程度减弱,说明系统的阻尼特性提高。然而,当锁相环参数在合理范围内,φT保持为正,表明锁相环的动态不会导致系统出现负阻尼。

综上,当构网型变流器的关键控制环在低频段提供滞后相位时,会导致同步机端口阻抗矩阵电抗分量也产生与同步机转速变化反向的转矩分量,这一相位滞后效应导致同步机出现负阻尼转矩。

3 提升阻尼的构网型变流器控制回路设计

根据第2 章的构网型MMC 低频振荡机理分析,基于所提出的阻尼转矩模型改造MMC 的关键控制回路,以提升系统的阻尼特性。

3.1 VSG 的阻尼控制器设计

对于VSG,其有功环和电压环均对系统阻尼特性产生影响。然而,只要有功环保持足够的Dv,VSG 能在模拟同步机转子摇摆特性的同时,避免低频振荡失稳。因此,需要对电压环设计阻尼控制器,如图6（a）所示,其中,PIvc表示电压控制的PI 控制器。根据2.3.1 节的分析,无功-电压下垂控制能改善系统阻尼特性,这主要是因为在电压环中引入了输出电流的反馈项。然而,过大的KQV会影响系统的电压调节特性。因此,图6（a）分别在d、q轴电压控制器引入了d、q轴输出电流的反馈阻尼控制GFI（s）,并且GFI（s）应当在低频段提供超前校正相位,因此选择其形式为:

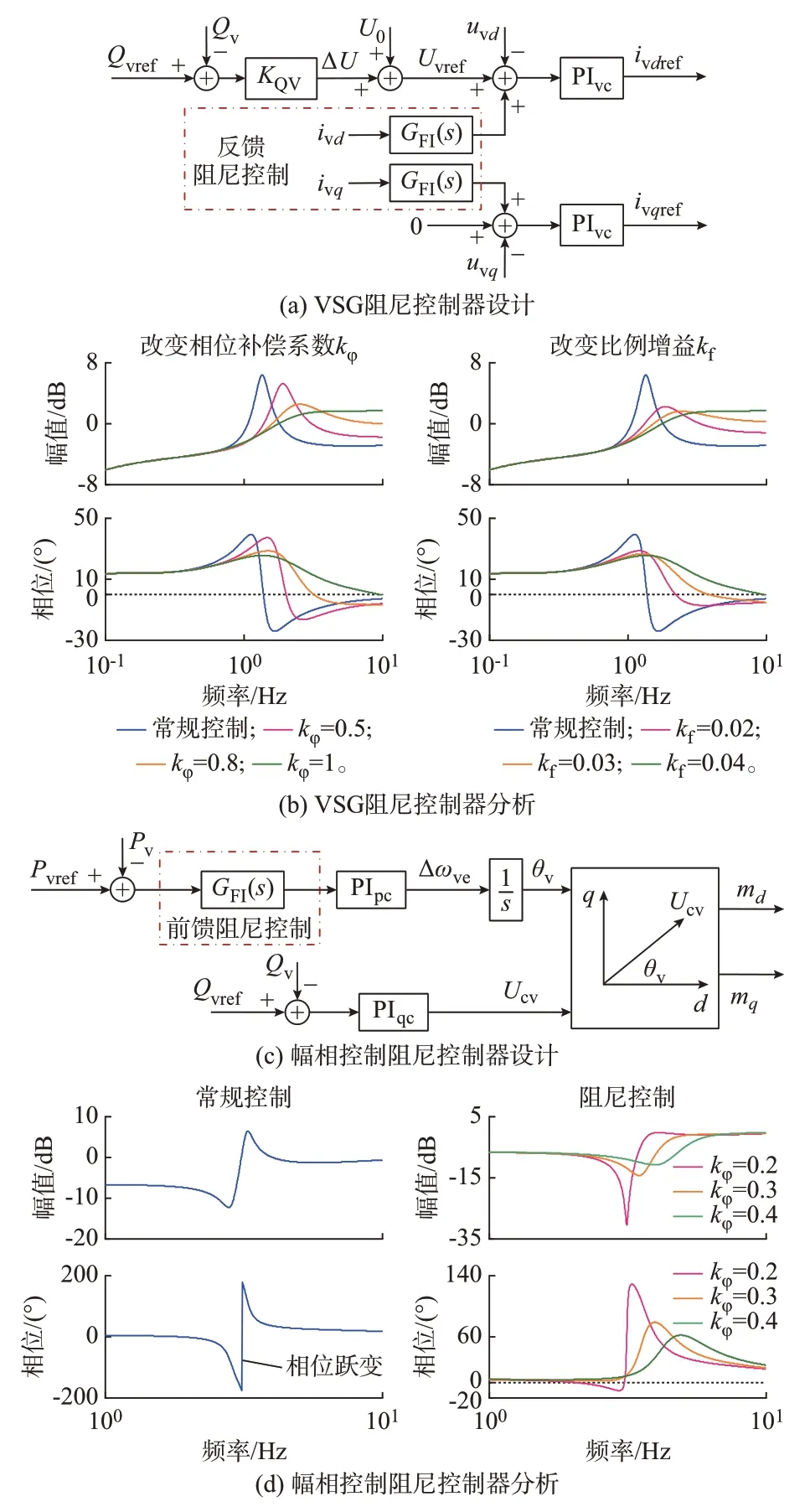
图6 构网型变流器阻尼控制器设计及参数分析Fig.6 Design and parameter analysis of damping controller for grid-forming converter

式中:kf与Tf分别为GFI（s）的比例增益和积分时间常数。

GU（s）在fd处的相位φU0为:

设GFI（s）在低频段的相位补偿系数为kφ,则其在低频段的相位φFI和参数Tf按式（19）确定。

研究GFI（s）的参数kφ和kf对阻尼特性的影响。当kf=0.04 时,改变kφ,MT（s）的幅频、相频特性曲线如图6（b）所示。在kφ从0.5 逐渐增大至1 的过程中,|MT（s）|的峰值减小,ΔTd逐渐增大,并且相位φT的滞后效应被消除,阻尼特性提升。因此,利用阻尼转矩模型能够确定合适的kφ并获得参数Tf。当kφ=1 时增大kf,阻尼控制器GFI（s）的效果更明显。然而,分析kf的影响时,还需要关注VSG 的电压-电流双闭环控制的稳定性。附录A 图A6 展示了kf变化时,系统中较为灵敏的特征根轨迹。图A6 表明,当kf增大时,一对特征根λ1、λ2将向右半平面移动,且临界稳定情况下kf为0.08。因此,增大kf虽然能够提升阻尼特性,但也可能导致控制器失稳。因此,参数kf的设计需要兼顾GFI（s）的效果和VSG 自身控制系统的稳定性,并且GFI（s）需要配备限幅环节,以保证故障下控制的稳定性。

3.2 幅相控制的阻尼控制器设计

对于幅相控制的MMC,其有功环会对系统阻尼产生影响。由于幅相控制仅采用单层控制环直接控制输出功率,为了保证控制系统的稳定性,在其有功-相位控制中引入前馈阻尼控制GFP（s）,如图6（c）所示,其中,PIpc和PIqc分别表示有功-相位控制和无功-电压控制的PI 控制器。根据2.4.1 节的分析,Gp（s）的相位滞后是引起系统负阻尼的关键因素。因此,为了改善低频段阻尼特性而不影响中、高频段的响应特性,GFP（s）采用超前校正装置:

式中:km、T1、T2分别为GFI（s）的比例增益、超前时间常数、滞后时间常数。

在fd处Gp（s）的相位φp0为:

同 样 地,设GFI（s）的 相 位 补 偿 系 数 为kφ,则GFI(s)的超前相位φFP,以及T1、T2的设计需要满足:

式中:β为相位整定系数。

由于GFP（s）级联在有功-相位控制器中,因此,km的整定需要保证其低频段幅值|GFP（s）|在1 附近。利用阻尼转矩模型研究GFP（s）的参数kφ对阻尼特性的影响。当参数Kp=1 且选取km=1 时,改变kφ,MT（s）的幅频、相频特性曲线如图6（d）所示。分析结果表明,当采用常规控制时,系统会出现负阻尼转矩分量,并且φT会穿越180°,发生相位跃变。而附加GFP(s)后,合适的kφ能够使得系统的ΔTd由负变正,提升系统的阻尼特性。

4 仿真验证

4.1 小系统仿真验证

为了验证理论分析结论的正确性,在PSCAD/EMTDC 中搭建如图1 所示系统的时域仿真模型,其中,系统参数见附录C 表C1。首先,验证所提阻尼转矩模型的准确性。在t=10 s 时,MMC 的功率指令值由200 MW 向下阶跃20 MW。当MMC 分别采用VSG、下垂控制和幅相控制时,时域仿真模型和阻尼转矩模型中MMC 的有功功率响应如附录D图D1 所示。图D1 表明,本文所提阻尼转矩模型与时域仿真模型在小干扰下的响应特性吻合度较高,证明其能够在运行点附近小范围内作为系统动态特性分析的有效工具。

研究当MMC 采用VSG 控制时,其电流环与电压环动态特性对系统阻尼的影响,此时在t=10 s 时改变相应控制器参数,同步机的角频率ωSG的仿真结果如附录D 图D2 所示。同时,本文采用Prony 分析法提取ωSG的各频率分量,并获得fd及相应的衰减系数ζ,其结果如附录C 表C2 所示。当ζ>0 时,表明系统存在负阻尼。当TU=0.08 时,分别改变VSG的参数TI、Tccsc,ωSG的仿真结果如附录D 图D2（a）和（b）所示。仿真结果显示,输出电流控制和环流抑制控制对系统的阻尼灵敏度较小,并且环流抑制控制的影响更小。因此,当系统出现低频振荡失稳时,仅通过改变电流环动态特性无法抑制振荡。相比之下,图D2（c）表明,改变TU对系统阻尼的影响更明显。当TU从0.05 增大至0.12 时,表C2 显示,fd减小并且ζ减小,系统阻尼增强,与理论分析一致。改变参数KQV,ωSG的仿真结果如图D2（d）所示。仿真结果表明,增大KQV能减小ζ,并且对fd的影响较小。因此,无功-电压下垂控制有利于抑制由电压环动态引起的低频振荡。

对比当MMC 采用VSG 控制和下垂控制时,其有功环对系统阻尼的影响,分别改变参数Dv与KPω,仿真结果如图7（a）和（b）所示。图7（b）中,在t=12.2 s 设置MMC 的电压指令值向下阶跃0.02 p.u.。图7 及附录C 表C2 表明,当Dv减小或KPω增大时,ζ均增大,表明系统低频段阻尼减弱。然而,VSG 的Dv改变会导致振荡失稳,而下垂控制则能保持低频段阻尼为正（ζ<0）。而且,当Dv=1/KPω时,VSG 的阻尼特性弱于下垂控制。因此,仿真结果印证了理论分析结果,即惯性系数Jv的引入导致VSG 和下垂控制对交流系统阻尼特性的影响有本质区别。

图7 VSG 和下垂控制有功环仿真结果Fig.7 Simulation results of active power loop of VSG and droop control

研究当MMC 采用幅相控制时,其有功-相位控制和无功-电压控制对系统阻尼的影响,分别改变参数Kp、Kq、Tq,ωSG的仿真结 果如附录D 图D3（a）和（c）所示。图D3（a）和表C2 说明,减小Kp可能导致系统出现负阻尼,并且fd在3 Hz 附近。研究无功-电压控制时在t=11.2 s 设置MMC 的有功功率指令值向下阶跃0.03 p.u.,并且保持Kp=5。图D3（b）和（c）表明,Gq（s）的参数Tq对系统阻尼的灵敏度高于Kq。然而,幅相控制的MMC 无功-电压控制器特性不会为系统提供负阻尼。改变σpll,ωSG的仿真结果如图D3（d）所示。仿真结果表明,锁相环动态特性不会导致系统出现低频振荡失稳现象。综上,仿真分析验证了理论结果,说明所提阻尼转矩建模及分析方法能够反映构网型MMC 对交流系统主导振荡频率、阻尼特性的影响。

4.2 多机互联系统算例验证

为了验证所提构网型MMC 回路改造方案对提升系统阻尼特性的效果,在PSCAD/EMTDC 中搭建如附录A 图A7 所示的4 机区域互联系统。构网型MMC 在节点10 并网,其输出功率Pmmc=400 MW,系统参数见附录C 表C3。仿真分析中,以近区同步机G4的角频率ωSG4为例进行模态分析。

研究VSG 的反馈阻尼控制器效果。在t=10 s时改变参数TU,图8（a）显示系统将出现振荡失稳现象,并且Prony 分析表明,TU从0.06 增大至0.12 时,fd从0.912 Hz 降 低 至0.812 Hz,ζ由0.095 3 降 低 至0.063 1。在定电压环设置反馈阻尼控制器,并选取GFI（s）的参数kφ=1,kf=0.05。在t=12.2 s 时设置Pmmc向下阶跃20 MW,参数TU改变时ωSG4的仿真结果表明,当MMC 功率指令值降低时,同步机G4转速下降。当采用反馈阻尼控制后,VSG 对系统的负阻尼效应消除,系统经历小扰动后能振荡收敛,阻尼特性改善。为了研究阻尼控制器的鲁棒性,以TU=0.06 为例,设置相位补偿系数kφ偏差±20%,ωSG4的仿真结果表明,当kφ的设置略有偏差时,GFI（s）依然能够为系统提供正阻尼转矩分量,抑制系统的低频振荡失稳。

图8 构网型MMC 阻尼控制器效果仿真分析Fig.8 Simulation analysis of damping controller effect for grid-forming MMC

研究幅相控制的MMC 前馈阻尼控制器效果。在t=10 s 时使得参数Kp由0.6 减小至0.3,ωSG4的仿真结果如图8（b）所示。Prony 分析结果表明,fd由2.308 Hz 降 低 至2.277 Hz,ζ由0.102 7 增 加 至0.188 3,系统阻尼特性逐渐恶化。在有功-相位控制环中加入前馈阻尼控制,并选取GFP（s）的参数kφ=0.4,km=1。在t=12.2 s 时 设 置Pmmc向 下 阶 跃20 MW,参数Kp改变时ωSG4的仿真结果表明,当采用前馈阻尼控制器后,相同参数Kp的情况下,系统阻尼由负变正,说明前馈控制器能够有效抑制由有功-相位控制引起的低频振荡。同样地,以Kp=0.3为例,设置kφ偏差±20%,仿真结果表明当kφ存在偏差时,GFP（s）能够使得系统阻尼由负变正,说明前馈阻尼控制器鲁棒性良好。

当t=10 s 时,设MMC 的PCC 分别发生对称故障（三相接地短路）和非对称故障（单相接地短路）,故障持续时间为50 ms,采用常规控制和阻尼控制时ωSG4的仿真结果如附录D 图D4 所示。仿真结果表明,当VSG 配备反馈阻尼控制器时,故障下系统阻尼优于常规控制；而当幅相控制的MMC 配备前馈阻尼控制器时,故障下ωSG4响应特性与采用常规控制接近。从而说明阻尼控制器在改善系统振荡特性的同时,对交流故障的鲁棒性良好。

5 结语

本文建立了适用于研究构网型变流器对系统低频振荡影响的通用模型,并提出了相应的阻尼分析方法。该模型能够从同步机视角归纳构网型变流器对系统阻尼的影响机理,从变流器视角为考虑关键回路的阻尼控制方案设计提供指导。该模型具备推广性,能够应用于分析不同类型的构网型变流器的低频阻尼特性。本文的主要结论如下:

1）构网型变流器的关键控制回路在低频段提供滞后相位时,能够导致同步机端口阻抗矩阵的电抗分量产生与转子转速变化反向的转矩分量,恶化系统的阻尼特性,引发系统低频振荡。

2）构网型变流器的有功环会影响系统的阻尼特性。相比VSG 的有功环,有功-频率下垂控制无惯性特性,不易引起系统低频振荡。幅相控制有功-相位控制环可能在低频段提供滞后相位并引起系统低频振荡,其机理与VSG 的有功环类似。

3）采用电压-电流双闭环控制的构网型变流器电压环对系统阻尼特性影响明显,并且其无功-电压下垂控制能够为系统提供正阻尼转矩。相比之下,采用单环控制的幅相控制的无功-电压控制环对低频段阻尼特性影响较小,不会引起振荡失稳。

4）根据不同控制环引起振荡的机理,为采用VSG 和幅相控制的构网型变流器设计了阻尼控制,并且基于阻尼转矩模型提出了参数整定方法。通过多机互联系统算例证明了其能够有效抑制低频振荡失稳,在参数改变和故障工况下鲁棒性良好。

在本文研究的基础上,后续将继续研究所提阻尼转矩建模、分析方法和判据在多机系统振荡评估中的应用,并聚焦含多类型构网型变流器的多机系统低频振荡模态辨识与定位等相关研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。