基于计量数据联合分布的用户无功补偿异常感知

张 傲，苏 盛，艾 渊，景 彪，李 彬，杨洪明

（1.电网防灾减灾全国重点实验室（长沙理工大学）,湖南省长沙市 410114；2.云南电网有限责任公司计量中心,云南省昆明市 650051；3.云南电网有限责任公司玉溪供电局,云南省玉溪市 653101）

0 引言

无功补偿可避免远距离传输无功功率带来的损耗,是电力系统经济运行的基础性措施。为提高配用电能效,一般要求电力用户按报装容量的20%～40%配置无功补偿装置,要求大工业用户和一般工商业用户分别达到0.9 和0.85 的功率因数,并根据达标与否按力调电费进行奖惩［1-2］。高能耗的大工业用户普遍重视无功管理,多可领取力调电费奖励；而海量的一般工商业用户往往缺乏必要的专业知识和运维人员,主要依靠无功补偿装置自动控制来保障用电能效。相当比例的用户无功补偿装置老化故障后,因不能及时感知和修复而长期带病运行,增大了电网线损和用户用能成本,例如,某中部年用电量为2×1011kW·h 的省份,2021 年电力用户因功率因数不达标,征收的力调罚款高达7.4 亿元。因此,及时准确感知用户无功补偿的故障异常,不但可以有效降低用户用能成本和电网运行损耗,还可促进社会有效投资,具有重要的工程应用价值［3］。

当前在电力设备的状态监测上已有大量研究,可基于红外测温［4-6］、超声波监测［7-8］和视频监测检出设备故障。但此类方法所需的状态量在用户侧均难以获取,因而不适用于用户侧的故障感知。既有月度电费账单中的力调电费信息,可提示用户无功补偿的故障异常。需要指出的是,以月度功率因数为无功补偿故障异常判据滞后性较强,须以月度为单位才得以识别,造成故障异常期间用电能效降低。而工商业用户基数庞大,亟需可及时感知无功补偿故障异常的能效提升方法。随着现有技术水平以及数据可用性的提升,根据不直接反映无功补偿运行状态的计量数据及时感知故障异常是可行途径。

当前,基于计量数据驱动的用电管理方面研究已较深入。文献［9-10］基于相邻用户电压存在关联性的特性对计量电压数据进行相似性分析,构建出户变关系特征,并采取聚类的方法识别出低压台区拓扑关系。文献［11-12］提出线损电量与用电量之间的归因分析方法,实现高损台区窃电用户的检测,在准确率和误报率上均表现良好。文献［13］通过对日计量无功功率和功率因数聚类实现无功故障日感知,但其对轻微故障场景识别不够灵敏,存在漏判。已有供电企业结合负荷大小和功率因数偏低进行告警,由于阈值设置困难,容易误报。联合分布特征可有效刻画变量间的潜在关联,在识别窃电用户［14］和风电出力预测［15］中表现良好,因此基于负荷大小与功率因数的联合分布特性进行分析,有可能及时地感知用户无功补偿轻微异常。

由于无功补偿装置按确定的控制策略进行投切控制,得到良好补偿的用户从电网吸收的有功负荷水平和功率因数之间往往具有确定的映射关系并服从特定的联合分布,而无功补偿异常会改变此种映射关系。因此,本文利用这种联合分布的改变来感知用户无功补偿的故障异常。首先,比较分析了无功补偿故障前后用户有功功率和功率因数联合分布的差异特征；然后,提出基于二维卷积神经网络（convolutional neural network,CNN）的计量数据特征矩阵分类方法；最后,基于3 个行业用户实际计量数据的仿真,验证了所提方法的有效性。

1 无功补偿装置故障异常特性分析

无功补偿装置主要包括静止无功补偿器（static var compensator,SVC）、静止同步补偿器（static synchronous compensator,STATCOM）和并联电容器组等,其中SVC 应用最为普及。无功补偿装置受安装工艺、过电压、过电流、积尘和设备老化等因素影响,会发生多种故障,最终一般会发展和表现为无法正常执行无功补偿功能,导致用户功率因数下降。

无功补偿装置根据用户三相负荷平衡程度可采用共补、分补及混补等3 种补偿电容控制模式,其中,前者适用于三相相对平衡的用户。由于工商业用户一般会考虑平衡三相负荷,三相共补在工程上应用最为普遍。下文将针对该模式下用户无功补偿装置的故障特性与感知分析展开研究。

无功补偿装置的投切策略以无功功率为主、功率因数为辅,通过比照系统所需无功大小与投切功率阶梯值以确定对应的投切容量,并以“循环投切”方式逐组投入电容器组直至满足目标功率因数［16-17］。按此控制策略,部分电容器组故障或投切开关无法正常投切时,未故障电容器组仍可投入工作。当功率因数低于切除功率因数且欠补功率大于阶梯容量的65%时,控制器投入电容器组；当功率因数高于切除功率因数且过补功率大于阶梯容量的50%时,控制器切除电容器组。用电设备运行时,有功功率与功率因数的电气公式如下所示:

式中:Qc为配置的无功补偿总容量；n为等容分组下的总分组数；λ为满足相应条件不等式的整数集合；max（λ）为投切组数即满足集合λ的最大整数；ΔQ为达到目标功率因数下的无功功率缺额；P为有功功率；Q为用电设备相应有功功率下的自然无功功率；Q1为无功补偿装置补偿的无功功率；ch为用电设备自然功率因数；c为补偿后的用电设备功率因数。

对于特定用户的用电设备,其自然功率因数为一稳定值,对应有功功率与自然无功功率大致呈正相关关系。无功补偿装置正常运作时,投切无功功率值Q1随自然无功功率的水平调整数值,以保持补偿后的功率因数维持在目标水平。因此,用户有功负荷水平P与补偿后的功率因数cosφ的联合分布蕴含着用户无功补偿装置运行状态信息。为直观呈现,将2 个典型用户的典型日负荷曲线以及无功补偿装置正常及故障时的有功功率p与功率因数c二维频率分布直方图绘制如图1 和图2 所示。图中:c与p从0 至1 表示功率因数和有功功率不断增大；u（p,c）表示离散化后有功功率与功率因数相应区间内的二维概率密度值。

图1 用户1 负荷曲线及有功功率-功率因数二维频率分布Fig.1 Load waveforms and active power-power factor two-dimensional frequency distribution of user 1

图2 用户2 负荷曲线及有功功率-功率因数二维频率分布Fig.2 Load waveforms and active power-power factor two-dimensianal frequency distribution of user 2

由图1 可知:

1）用户1 夜间轻载时负荷达不到无功投切门槛值,维持在自然功率因数的低水平上,对应图1（b）和图1（c）的右侧。由于夜间轻载时段持续时间长,因此,处于该状态的频率明显高于其他状态。

2）图1（b）中,负荷水平提高至0.4 p.u.以上时,无功补偿装置正常进行补偿投切,功率因数得到明显提高。有功负荷增长后无功补偿作用使得功率因数散布于较高区间,在频率上明显低于轻载时段。

3）图1（c）中,用户部分无功补偿回路无法正常投切,有功功率达到0.6 p.u.以上时无法满足需求的无功补偿,功率因数逐渐降低。重载较低功率因数的时段在持续时间上因为分布的空间被压缩,在频率上反而如图1（b）左上侧所示有所抬高。

由图2 可见:

1）与用户1 类似,用户2 在轻载时的功率因数在低位徘徊,但在有功功率轻微抬升后功率因数即从0.2 以下跃升到0.2～0.4 之间。

2）负荷水平提高到0.4 p.u.以上时,无功补偿使用户功率因数明显提高,功率因数散布于较高区间内。

3）无功补偿装置故障时,功率因数随负荷增长而快速下滑,整体形态特征与用户1 类似。由于无功补偿电容器故障组数更多,有功功率在0.5 p.u.时功率因数即已滑落至低位。

综上分析可知,尽管用户用电特性各不相同,但重载情况下无功补偿装置异常造成的功率因数下滑总会造成用户有功功率/功率因数联合分布的形态扭曲。通过检测用户计量数据的联合分布的形态变化,有可能感知无功补偿装置的故障异常。

2 基于二维CNN 的特征矩阵分类方法

以下利用有功功率与功率因数频数分布矩阵标识和分析无功补偿装置正常和故障情况下装置运行状态。首先利用CNN 多层提取特征能力提炼正常及故障状态下矩阵元素的分布情况,以感知无功补偿装置的故障异常状态,详细说明如下。

2.1 P-cos φ频数分布矩阵生成及分析

统计学中常使用频数或频率信息来表征一维或多维变量的边缘及联合分布特性。为量化无功补偿装置正常及故障状态下的有功功率及功率因数分布特性,根据智能电表计量用户用电数据,按以下步骤生成频数分布矩阵刻画有功功率与功率因数的联合分布。

1）定义两组维度为n×1 的电气量矩阵数组P=[p1,p2,…,pn]T、C=[c1,c2,…,cn]T,其 中n为该数组包含的智能电表总采样点数,P和C分别为有功功率和功率因数矩阵。

2）对矩阵进行标准化操作如下:

式中:min {P}为P中最小值；max {P}为P中最大值；min {C}为C中最小值；max {C}为C中最大值；pi为采样点i的有功功率；ci为采样点i的功率因数；pbi为标准化后采样点i的有功功率；cbi为标准化后采样点i的功率因数；Pb为标准化后的有功功率矩阵；Cb为标准化后的功率因数矩阵。

3）经过标准化操作后,令β=[Pb,Cb]并将Pb和Cb均匀分成o及p份得到两份区间集合如下:

式中:Pbi为Pb分割后的某份区间；Cbi为Cb分割后的某份区间。

4）定义o×p个集合Aij=（i,j）（i=1,2,…,o；j=1,2,…,p）,对 于 矩 阵β中 第l个 行 向 量βl=[pbl,cbl],若pbl属于区间集合Pbi且cbl属于区间集合CbJ,则将βl归为集合Aij内。

5）按照步骤4）将矩阵β内所有行向量归化至集合Aij后,整合出共o×u个子区间集合内各累计的行向量个数。

经过上述步骤后,生成P-cosφ频数分布矩阵为:

式中:Ni,j为某个集合内累计的向量个数。

2.2 二维CNN

CNN 是深度学习中应用广泛的一种学习方法,在异常检测、数据贴补等多领域有广泛应用［18-23］。按处理的数据维度信息可分为一维、二维及三维CNN。其中一维CNN 主要用于序列数据的处理分析,二维CNN 常用于图像数据的处理,三维CNN 用于视频及动作数据的处理。

二维CNN 框架主要由卷积层、激活层、池化层、全连接层等构成。其中,卷积层、激活层和池化层处于CNN 核心位置。卷积层与激活层通常作为一个特征抽取组合通过卷积核按一定步长滚动遍历输入的图像像素点矩阵进行卷积、激活操作以映射出有效特征。卷积及激活操作可通过下式表现［24］:

式中:G（·）为ReLU 激活函数；wkl为某个卷积核矩阵；xkl为某个图像矩阵；b为卷积偏置。

池化层也称下采样层,通过对卷积层输出的特征进行池化降维操作以提升网络运行效率并防止过拟合。利用有功功率-功率因数联合分布特征引入二维CNN 将频数分布矩阵作为网络输入,通过多层训练分类实现无功补偿装置的异常感知。

2.3 基于二维CNN 的特征矩阵识别

基于二维CNN 的特征矩阵识别框架包含标签数据集的构建和卷积网络结构层次搭构两部分。标签数据集包括用于正常、故障样本标签及各标签下有功功率和功率因数特征矩阵数组。以“1”和“0”代表正常和故障状态进行数据标签。采取滑窗方式对有功功率/功率因数数组进行滑动遍历并生成特征矩阵,其中滑窗方式生成标签数据集的特征矩阵示意图如图3 所示。

图3 滑窗方式生成特征矩阵示意图Fig.3 Schematic diagram of feature matrix generated by sliding window mode

本文构建的二维CNN 由输入层1 层、卷积层2 层、池化层2 层、激活ReLU 层2 层、全连接层1 层及1 层输出层构成。网络各层参数详列如表1所示。

表1 二维CNN 各层输入、输出及参数结构信息Table 1 Input, output and parameter structure information of each layer of two-dimension CNN

采用reshape 函数对生成的P-cosφ频数分布矩阵进行重组样本数操作,以获得若干个维度为8×8的子集矩阵,并将其送至输入层。设定卷积核大小为5×5,子集矩阵经过每次卷积和激活操作后,送入池化核为2×2 的最大池化层。采取“same”方式,经过两次卷积池化操作后,得出2×2×64 的三维特征图并送至全连接层操作进行拉伸特征维度。最终采取Adam 作为梯度优化器更新网络结构参数后,利用softmax 函数预测概率分布,分为“1”（正常）和“0”（故障）两个类别。

结合标签数据集和CNN 的结构层次构建后,即可得出整体检测方法框架如图4 所示。图中:在基于正常和故障数据样本库按照图4 方法生成Pcosφ联合矩阵数据集后,在样本标签数据集中选取一定比例的样本作为训练集和测试集输入CNN 模型进行训练测试,经过多次卷积、池化等操作后,输出预测结果并评价模型,最后通过验证集来进行实例验证。

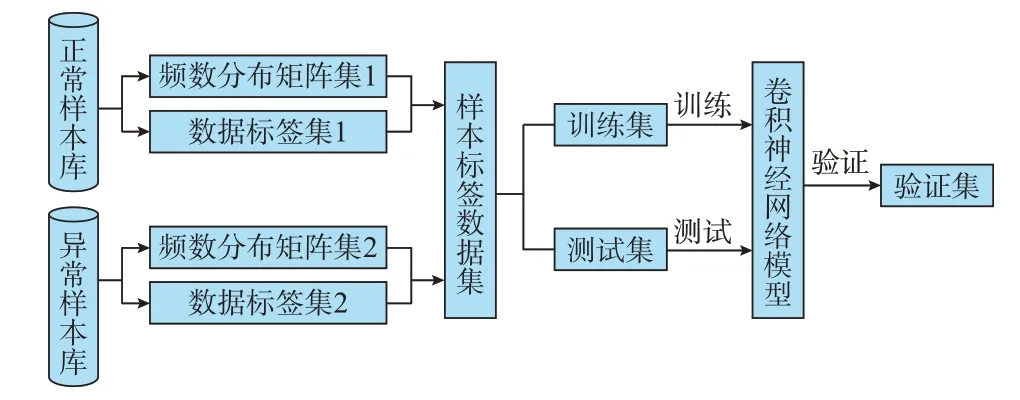
图4 检测方法框架Fig.4 Framework of detection method

3 测试仿真

算例测试分为基于仿真数据的CNN 模型训练、测试算例以及基于实际正常和故障数据的验证算例。其中,仿真算例数据为基于无功补偿控制策略按不同故障程度对某地区行业用户用电数据仿真而得到,验证集算例数据取自现场取得的正常及故障数据。本文通过仿真数据搭建频数分布矩阵CNN模型,并通过实际故障用户数据验证模型的普适性和有效性。

3.1 仿真数据训练算例

仿真算例的训练框架包含仿真数据的生成和标签数据库的构建训练两部分。对某地区3 个来自化纤制造行业、土木工程行业用户的计量数据,按本文方法进行仿真模型的搭建训练与测试。其中,仿真数据的生成流程框图见附录A,具体操作如下。

1）获取用户智能电表实际15 min 间隔采样的有功功率数据与用户变压器报装容量值。

2）以用户报装容量的40%作为无功补偿配置总容量设定值。采取循环投切控制策略,设置分组数为8 组的等容分组方式仿真正常投切下的无功功率。

3）分别以35%、35%和30%的比例按2 组电容器无法正常投入回路、3 组电容器无法正常投入回路和4 组电容器无法正常投入回路的故障程度仿真生成无功补偿异常的无功功率数据［25-26］。

4）基于用户有功数据与前述步骤生成的正常、异常投切方式下的无功功率计算功率因数,得到正常、异常有功功率-功率因数联合分布。

对仿真生成的有功功率、功率因数数据进行标准化操作后,设定24 h 为子集矩阵样本时间跨度,采取滑窗方式以4 h 滑窗长度读取子集矩阵样本。仿真模型数据的几种典型样本如图5 所示,由图可知仿真生成样本的联合分布特征基本与前述分析一致。

图5 轻载/重载时卷积模型样本概率密度Fig.5 Sample probability density of convolutional model at light load and heavy load

以320 d 和160 d 为训练集和测试集时间跨度,设置模型中正常和故障样本的比例为1∶1,每个子集分布矩阵维度为8×8,训练集总样本个数为1 920 个,测试集总样本个数为960。将生成正常和故障标签下的频数分布矩阵数据集输入CNN 模型,并经迭代训练建立稳定模型供实例验证。

3.2 无功补偿装置故障用户现场数据验证算例

用户无功补偿装置严重故障时,会导致用户功率因数的明显异常,容易诊断识别,以下选择化纤织造、水泥石膏、土木工程行业3 个用户在无功补偿正常和发生轻微故障异常时各15 d 的计量数据进行测试验证。测试的故障感知结果如表2 所示,在所有用户的无功补偿装置正常日均做出正确判断,无功补偿装置轻微故障时,对用户2 和用户3 有两个故障日漏判为正常。因正常日无误判,以下将3 个用户的无功补偿故障日有功功率与功率因数数据绘制于图6。由图6 可得出以下结论。

表2 3 个用户验证集诊断结果对比Table 2 Comparison of diagnosis results of verification set among three users

图6 用户故障样本有功功率和功率因数曲线Fig.6 Waveforms of active power and power factor for user’s fault sample

化纤织造用户无功补偿故障时,在用户轻载条件下功率因数可保持0.9 以上的正常水平,但重载时,尤其是每天尖峰用电时刻的功率因数水平会出现明显跌落,从而导致在有功功率和功率因数的二维频数分布矩阵中更多的频数分布在矩阵右下角。因每个故障日均存在能体现故障特征的尖峰负荷,对该用户的故障检测率为100%。

水泥石膏用户故障样本除第7、8 天外均运行于重载条件下。由于该用户用电负荷日周期相对平稳,仅在负荷尖峰时刻出现局部功率因数跌落,因此判别为异常。轻载的第7、8 天,投切部分完好的无功补偿回路即可将功率因数维持在高位,漏判为正常。

土木工程行业用户用电有明显的日周期,与化纤织造用户同为单峰电力用户,但昼夜峰谷差距明显。尽管日均功率因数可以达标,但日尖峰时段对应的功率因数跌落,仍可有效揭示无功补偿装置的故障异常。在表现出尖峰负荷故障特征的时间段较少的工作日仍被判断为无功补偿装置正常的工作日,造成了两天的漏报。

为分析算法模型在不同故障比例下的敏感性及普适性,分别设置30%和10%的故障样本比例进行验证分析。两种故障比例下模型的验证结果分别如表3 和表4 所示。

表3 30%故障比例验证结果Table 3 Verification results with 30% failure ratio

表4 10%故障比例验证结果Table 4 Verification results with 10% failure ratio

故障设置比例为30%时,除去用户2 正常标签天数中产生的4 d 误报,其余用户对正常及故障标签天数均准确识别。

故障设置比例为10%时,用户2 及用户3 中分别产生2 d 和1 d 的误报,其余情况均准确识别。

模型在30%及10%故障样本比例下的识别效果对比50%故障样本比例下的识别效果,故障日的识别准确率得到提升而对于正常日的识别出现了少许误报。

为进一步体现采取本文算法模型的必要性,采用本文方法对月力调罚款用户以第1 天起,逐天地将该用户计量数据初始化后送入模型进行诊断识别,当输入第8 天计量数据时,第1 次诊断为异常标签。绘制该用户前8 天有功功率及功率因数曲线图,如图7 所示,其中故障标签时段以虚线框区域标注。

图7 正常运行至故障日有功功率、功率因数曲线Fig.7 Waveforms of active power and power factor from normal operation day to failure day

由图7 可知,采取本文方法可在故障发生的早期实现感知,而月度功率因数需要在月末或下月份才可察觉故障异常,因此本文方法可更及时、敏锐地精确感知无功补偿故障异常,提高用电能效。

3.3 对比实验

混淆矩阵及其衍生指标为异常检测类问题的常用评价指标。在混淆矩阵基础上,选取准确率（αACC）、命中率（αTPR）、误检率（αFPR）、召回率（αF1）作为模型评价指标,各指标诠释意义见表5,计算公式如下:

表5 混淆矩阵指标诠释Table 5 Indicator interpretation of confusion matrix

式中:TP为实际无功补偿装置异常且检测为异常的样本数；FP为实际为正常但被检测为异常的样本数；FN为实际为异常且被检测为正常的样本数；TN为实际为正常且预测为正常的样本数。

为对比验证本文基于联合分布特性选取特征量的方法对复杂场景的适用性,仍采用3.2 节的3 个行业用户设置50%的故障比例样本,分别采用单一功率因数以及有功功率与功率因数二维数组形式作为二维CNN 的输入量以及文献［27］采取的支持向量机（SVM）学习方法进行对比,得到4 项检测评价指标对比如表6 所示。由表6 结果可得出以下结论:

表6 评估指标结果比对Table 6 Comparison of evaluation indicator results

1）采用单一功率因数的方法未考虑到轻载时刻功率因数偏低为正常现象,误检率达到了15.56%且检出率明显低于本文所提方法。

2）采取有功功率与功率因数的二维数组作为模型输入,虽然蕴含了轻载时刻的正常特性,但部分无功补偿故障仅在重载时段有所表现,而用户重载时刻较为随机分散,不进行特征提取而仅采用有功功率及功率因数二维数组作为输入容易漏报,准确率相比本文方法低了4.45%。

3）采取SVM 的学习方法与采用联合数组进行学习类似,在故障期间较少的时刻表现较差。

4）本文构建的特征量为累计分布特征,可更好地适应故障时刻分散的场景,具有更优秀的检出和误报率。

4 结语

针对缺乏专业知识的电力用户难以及时感知自身无功补偿装置故障异常、降低用电能效和提高用能成本的问题,提出了基于计量数据中有功功率与功率因数联合分布的用户无功补偿异常感知方法。

1）分析指出既有电力设备故障检测方法需要采集状态量监测数据,难以适用于用户侧无功补偿装置的故障感知,需要应用已有计量数据感知无功补偿装置的故障异常。

2）利用无功补偿装置正常和故障时用户有功功率和功率因数联合分布存在明显差异的特点,提出了基于二维CNN 特征矩阵分类的无功补偿装置故障感知方法。

3）基于实际用户数据的测试分析表明,所提方法可有效检出少量无功补偿回路投切异常的轻微故障,相比采用单一功率因数和有功功率及功率因数联合数组进行异常检测,在准确率和误报率上均表现更优。

本文探索提出了利用计量数据识别用户无功补偿异常的初步方法。随着物联网和人工智能技术的发展,数据可用性和异常检测的能力已得到显著提升,通过挖掘计量数据的内在价值有可能普遍性提高用户功率因数,实现数据赋能的用户能效提升。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。