考虑用户响应不确定性的园区综合能源系统分布鲁棒低碳调度

晋旭东，孙 磊，丁 明，文福拴，孙 伟

（1.合肥工业大学电气与自动化工程学院,安徽省合肥市 230009；2.新能源利用与节能安徽省重点实验室,安徽省合肥市 230009；3.合肥综合性国家科学中心能源研究院,安徽省合肥市 230031；4.浙江大学电气工程学院,浙江省杭州市 310027）

0 引言

化石燃料短缺与环境污染问题已引起国际社会普遍关注［1］。能源行业是碳排放的重要主体,减排责任重大［2］。近年来,具有较高能源利用率和可再生能源消纳水平的园区综合能源系统（integrated energy system,IES）受到学术界和工业界的广泛关注［3］。

IES 的低碳经济调度策略能够提高系统的经济效益和环境效益,为实时系统控制提供重要参考［4］。目前,已有一些关于IES 低碳经济调度策略的研究报道［5-7］。文献［8］提出能源枢纽/中心的概念,通过耦合矩阵描述系统多能流输入输出的关系,并提出了具有一般性的IES 优化模型。文献［9］分析并论证了电转气（power to gas,P2G）设备的能量转换和时空平移能力,建立了削峰填谷模型以平滑系统负荷曲线。文献［10］提出了考虑碳交易的IES 低碳经济调度模型,兼顾了系统运行的低碳性和经济性。不确定性因素会影响园区IES 的优化调度结果,分布鲁棒优化因其综合了随机优化和鲁棒优化的优点,得到了广泛应用［11］。文献［12］建立了两阶段分布鲁棒调度优化模型,并提出了备用容量配置的可行性校核子问题。现有基于分布鲁棒的IES 优化调度研究大多考虑可再生能源机组出力的不确定性,未能充分考虑IES 运行中存在的其他不确定性因素。

综合需求响应（integrated demand response,IDR）能够有效调动用户侧潜力,有助于维持系统运行的安全性［13］、提升消纳可再生能源发电的能力［14］,可有效提高IES 运行的经济性和灵活性［15］。因此,在园区IES 的低碳调度策略中应充分考虑IDR［16］。文献［17］建立了基于IDR 的多主体博弈模型,实现了系统管理机构、用户和产能基地的利益互相制约与联合优化。文献［18］构建了基于用户舒适度的IDR 模型,所提出的联合热电响应模型有助于引导用户调整其负荷需求,进而降低系统运行成本。虽然已有一些考虑IDR 的园区IES 低碳经济调度策略的研究报道,但现有研究未考虑到不同用能习惯用户的响应能力和响应意愿对IDR 的影响。

IDR 程度的不确定性是园区IES 低碳经济调度优化模型需要考虑的重要因素［19-21］。文献［22］考虑了信息物理系统和用户响应不确定性对负荷聚合商的影响,采用蒙特卡洛模拟方法计算负荷聚合商在不同可靠性要求下的经济激励水平,进而求解得到最优激励价格。文献［23］基于证据理论对需求响应程度的不确定性进行建模,提出了兼顾设备配置和运行优化的双层协同规划模型,进而有效提升系统抵御风险的能力。然而,现有的IES 调度模型中均未考虑用户响应程度的不确定性对园区IES 多能平衡约束的影响,难以真实反映在用户需求响应程度不确定情况下园区IES 中不同类型能源的功率流动。

在上述背景下,本文首先提出考虑碳交易和IDR 的园区IES 运行架构,并构建计及用户用能习惯的IDR 模型。然后,建立以最小化系统运行成本为目标函数并考虑系统运行约束的园区IES 低碳经济优化调度模型。最后,在考虑用户响应程度不确定性的情形下,提出园区IES 低碳经济调度的分布鲁棒优化模型,并转换为混合整数二阶锥优化模型,从而可采用商业求解器有效求解。

1 考虑碳交易和IDR 的园区IES 运行架构

本文所研究的园区IES 包含电、气、冷、热多能源的耦合,其架构如图1 所示。图中:Eelc、Ggas和Hheat分别为系统外购的电能、天然气和热能的相应功率；EP2G,GH为P2G 设备产生的掺氢燃气经热量换算得到的功率；Delc、Dheat和Dcool分别为用户的电、热和冷功率需求；λelc为电价；ΔDelc、ΔDheat和ΔDcool分别为电、热和冷功率需求的改变量。系统中的主要设备包括电力变压器（transformer）、热电联产（combined heat and power,CHP）设备、燃气锅炉（gas boiler,GB）、P2G 设备、风电机组（wind turbine,WT）、光伏发电（photovoltaic,PV）、电 热 泵（electric heat pump,EHP）、中央空调（air conditioner,AC）、吸收式制冷机（absorption refrigerator,AF）和 换 热 器（heat exchanger,HE）。本文假设AC 设备只用于制冷。

图1 电、气、冷、热多能源耦合的园区IES 架构Fig.1 Framework of park-level IES with multi-energy complementation of electricity, gas, cooling and heat

由于热能价格和天然气价格在短时间周期内可认为是固定值［16］,本文仅考虑通过优化系统运营商售电价格引导用户调整用能习惯,并优化系统内各设备的运行工况。园区IES 的多能用户通过响应最优的购能价格调整其用能需求。在上述系统运行架构的基础上,引入碳交易和IDR 机制,实现园区IES低碳经济运行。

1.1 阶梯碳交易机制

碳排放交易是指运用市场手段实现低碳环保目标的一种机制［24］。初始碳排放配额的确定是碳交易的基础与关键步骤,现有方法主要包括基准线法、历史法和拍卖法。其中,基准线法［25］根据行业碳排放强度进行配额分配,能够在合理增加企业碳排放成本的同时引导低碳环保生产。本文采用基准线法确定碳交易配额。

在图1 所示的园区IES 中,主要的碳排放源包括外购电 能、CHP 设备以及GB［26］。园区IES 的日无偿碳排放配额N*可描述为:

式中:N*elcbuy、N*CHP和N*GB分别为外购电能、CHP 设备和GB 的日无偿碳排放配额。

园区IES 的实际日碳排放量包括外购电能、CHP 设备以及GB 的碳排放。此外,园区IES 内的P2G 设备本身具有一定的吸碳能力［5］,有助于减少系统的碳排放量。园区IES 实际的碳排放量N可描述为:

式中:Nelcbuy、NCHP和NGB分别为外购电能、CHP 设备和GB 的碳排量；EMRt为t时段输入甲烷反应器（methane reactor,MR）的氢气量；Eelct为t时段外购的电功率；GCHPet和GCHPht分别为t时段CHP 设备用于发电和产热消耗的天然气功率；GGBt为t时段GB消耗的天然气功率；ηCHPe和ηCHPh分别为CHP 设备的发电效率和产热效率；ηGB为GB 的效率；βelc和βh分别为单位电量和单位热量的碳排放系数；φe,h为CHP 设备发电量向发热量的折算系数［27］；βg为甲烷反应器的碳捕获系数［28］；T为调度周期。

本文采用阶梯碳交易机制分析系统的碳排放［29］,阶梯碳交易如附录A 图A1 所示。

1.2 IDR

基于价格弹性理论,本文通过优化系统运营机构的售电价格引导用户参与需求响应,同时根据不同种类用户的用能习惯,确定不同用户在不同时段的各类能源需求调整的响应量。用户的响应能力和响应意愿可以从消费者心理学的角度进行分析。根据马洛斯需求理论［30］可知,用户首先购买产品或服务以满足其基本需求,然后继续购买以满足习得需求；根据边际效益递减规律［31］可知,用户从每一相继单位的物品中得到的效用都比前一单位所得的效用小,有递减的倾向。因此,本文假设某用户在某一时段的热负荷和冷负荷需求越大,其以电负荷替代冷、热负荷的意愿就越高。

不同用能习惯的用户对以冷、热负荷替代电负荷的响应能力不完全相同,这里根据用户用能习惯将用户分为a、b、c三种类型［17］。为定量描述用户对以冷、热负荷替代电负荷的能力,引入第i类用户在t时段的电热替代系数δe2hi,t和电冷替代系数δe2ci,t,其定义分别如式（6）和式（7）所示。

式中:Delci,t、Dheati,t和Dcooli,t分别为t时段第i类用户参与需求响应前的电、热和冷负荷。为更好地描述用户用能偏好的相对关系,对δe2hi,t和δe2ci,t进行归一化处理,将其映射到区间［0,1］,其数值越趋近于0,则表示用户以电负荷替代冷、热负荷的意愿越弱；其值越趋近于1 则表示用户以电负荷替代冷、热负荷的意愿越强。

本文通过调节冷、热负荷需求补偿电力负荷的部分响应量,以减少园区IES 运营商为参与IDR 的电力负荷支付的费用。a类型用户的用能习惯及其说明见附录A 图A2。由于用户侧存在无法替代的刚性负荷［32］,用户冷、热负荷的总替代量应小于用户的可响应电负荷量,如式（8）所示。

式中:δi为第i类用户可响应电负荷占总电负荷的比例。

根据需求价格弹性矩阵［33］,第i类用户在t时段的电负荷响应量ΔDelci,t可由式（9）表示。

式中:ψt为t时段用户的响应程度；εt,τ为t时段与τ时段间的电价弹性系数,当t=τ时为电价自弹性系数,否则称为电价互弹性系数；λelcτ为τ时段的基础电价；Δλelcτ为τ时段的电价变化量。

综上所述,第i类用户在t时段电、热、冷负荷的响应量和参与需求响应后的实际负荷需求量可由式（10）和式（11）表示［16］。

式中:ΔDheati,t和ΔDcooli,t分别为第i类用户在t时段的热负荷和冷负荷需求响应量；Delc,Fi,t、Dheat,Fi,t和Dcool,Fi,t分别为第i类用户在t时段参与需求响应后的电负荷、热负荷和冷负荷需求。

2 园区IES 优化调度模型

2.1 目标函数

所提出的园区IES 优化调度策略以最小化系统运营机构总的日运行成本为目标,即

式中:C为园区IES 的总运行成本；Cbuy为向上级能源网络购能的成本；Cwater为园区IES 用水成本；Ccarbon为碳交易成本；Cpena为弃风弃光惩罚成本；Ccomf为IDR 成本。上述成本的计算方法具体描述如下。

1）购能成本

考虑到分时电价已广泛应用于电力行业,但天然气和热量价格仍以固定价格为主。因此,园区IES 的购能成本可由式（13）计算。

式中:Ggast和Hheatt分别为t时段外购的天然气功率和热功率；Celct为t时段的外购电价；Cgas和Cheat分别为外购天然气价格和热量价格；Δt为离散化的时间间隔。

2）用水成本

由于P2G 设备电解水以及GB、EHP、HE、AF等设备的冷却与传热需要消耗大量水,需考虑用水成本［34］,其可由式（14）—式（16）计算。

式中:ΩD为以水作为热传导介质的设备集合；cpwt为单位体积水价；WP2Gt为t时段P2G 设备电解水的用水量；Wt,d和Et,d分别为t时段设备d的用水量和耗能；EP2Gt为t时段P2G 设备消耗的电功率；ηEL为电解槽（electrolyzer,EL）效率；qH2为氢气热值；δ为额定工况下生成单位体积氢气的用水量；ηd为设备d的运行效率；Sw,hc为水的比热容；Tint,d和Toutt,d分 别 为t时段流入和流出设备d的水的温度。

3）碳交易成本

阶梯碳交易成本的计算方法如式（17）所示。

式中:c为碳交易基准价格；α为碳交易价格的增长系数；q为碳交易价格区间的长度。

式（17）所描述的阶梯碳交易成本是一个非线性分段函数,可采用big-M 法进行线性化处理。

4）弃风弃光惩罚成本

式中:cpen为弃风弃光的惩罚系数；Ppvforet和Pwtforet分别为t时段光伏和风电的预测功率；Ppvt和Pwtt分别为t时段光伏和风电的消纳功率。

考虑到本文的研究对象是园区IES,其季节情况和地理位置比较固定,且有较多先进的风光发电出力预测方法保证预测精度,本文假设光伏和风电的预测功率是确定性的参数。

5）IDR 成本

式中:λdr为需求响应成本系数。

式（19）表示园区IES 运营商支付给用户的IDR费用的计算方法。针对参与电力需求响应的用户,IES 运营商将为其补偿一部分冷、热负荷,进而减少IDR 的费用。

2.2 系统运行约束

1）电功率平衡约束:

式中:ηT为变压器效 率；EEHPt和EACt分别为t时段EHP 和AC 消耗的电功率。

2）天然气功率平衡约束:

式中:ηMR为甲烷反应器的效率。

3）考虑燃料掺氢的两阶段P2G 运行约束

在所提出的考虑燃料掺氢的两阶段P2G 模型中,电解槽产生的一部分氢气进入甲烷反应器与CO2合成甲烷,另一部分氢气与合成的甲烷混合,构成掺氢燃料［35］,为CHP 设备和GB 提供燃料。图2展示了考虑燃料掺氢的两阶段P2G 模型。通过改变掺氢比例实现对P2G 设备运行方式的灵活调节。

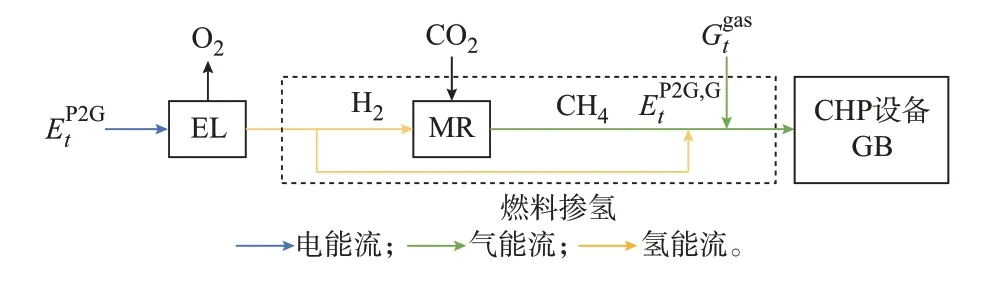
图2 考虑燃料掺氢的两阶段P2G 设备模型Fig.2 Two-stage model of P2G devices considering hydrogen doping in fuel

所提出的考虑燃料掺氢的两阶段P2G 模型可由式（22）表示。

式中:EP2G,Gt为t时段由P2G 设备产生的天然气流量经换算得到的天然气功率。

掺氢天然气中的掺氢比例须满足安全燃烧要求［35］,可由式（23）表示。

式中:γmin和γmax分别为掺氢比例的最小值和最大值。

4）热功率平衡约束:

式中:HHEt和HAFt分别为t时段HE 和AF 的输入功率；ηEHP和ηHE分别为EHP 和HE 的效率。

式（24）和式（25）分别为园区IES 供给侧和需求侧的热平衡约束。

5）冷功率平衡约束:

式中:ηAC和ηAF分别为AC 和AF 的效率。

6）系统购能和设备运行约束。其中,式（27）表示园区IES 外购能量的最大值约束；式（28）表示系统设备容量约束；式（29）表示设备出力的爬坡约束。

式中:ΩP为园区IES 外购的能源种类集合,包括电、热和天然气；ΩS为园区IES 设备集合,包括CHP、GB、P2G 等 设 备；Ep,t为t时 段 外 购 能 源p的 功 率；Emaxp为外购能源p的功率上限；Es,t为t时段设备s的输入功率；Emins和Emaxs分别为设备s输入功率的最小值和最大值,其中天然气和氢气根据热值换算为电功率；Ddowns和Uups分别为设备s爬坡率的最小值和最大值。

7）风电与光伏的出力约束。其中,式（30）和式（31）分别表示t时段园区IES 消纳的光伏出力和风电出力均小于其预测值。

8）电价变化量约束。式（32）约束了园区IES 电价调整范围。

式中:Δλe,min和Δλe,max分别为电价变化量的最小值和最大值。

3 考虑用户响应不确定性的分布鲁棒优化模型

用户认知和消费差异性等因素会使得用户参与IDR 的程度存在较强的不确定性［23］。现有的处理不确定性因素的方法主要包括随机优化方法［36］和鲁棒优化方法［37］。采用随机优化方法时,随着场景的增加,可能导致维度灾难和计算时间过长；而采用鲁棒优化方法得到的结果则过于保守。为了克服随机优化方法和鲁棒优化方法的局限与不足,分布鲁棒优化理论作为一种新的不确定性处理方法,近年来备受科研工作者的关注［38］。

本文考虑的不确定性参数为t时段用户参与响应的程度ψt。在将所提出的确定性模型转换为分布鲁棒优化模型之前,需做两个方面的处理:1）引入辅助变量zt,为不确定性参数ψt的倒数,表示t时段用户参与需求响应的抗拒意愿,其定义如式（33）所示；2）引入大于0 的辅助变量λelc,Fτ,其含义为τ时段的最优电价,定义如式（34）所示。

基于上述处理方法,可分别将确定性模型中与不确定性参数相关的式（20）、式（25）和式（26）转换为式（35）—式（37）。

进而,将所构建的分布鲁棒优化模型描述为:

式中:EP（·）表示求数学期望；P为zt的概率测度；Γ为模糊集；μt和ηt分别为zt的一阶矩和二阶矩；Ωt为不确定性参数的集合；gt为zt的最大值。

在所建立的分布鲁棒优化模型中,第1 阶段决策变量包括系统设备出力Es,t、外购能源对应的功率Ep,t、消纳的光伏和风电功率Ppvt和Pwtt、实际碳排量N和阶梯碳交易成本线性化引入的辅助变量（含布尔变量）,第2 阶段决策变量为最优电价λelc,Fτ。

由于所建立的min-max-min 三层两阶段模型难以直接求解,现有的处理方法主要包括Benders 分解［39］、列 与 约 束 生 成（column and constraint generation,C&CG）算法［40］,但其主、子问题迭代求解的方式存在收敛时间长、求解精度不高的问题。为提高模型的求解精度和效率,可基于对偶理论将式（38）—式（42）描述的两阶段分布鲁棒优化模型转换为混合整数二阶锥优化模型［41］,如式（43）—式（52）所示。

式中:k、ut、vt、ωt、rt和s均为对偶变量。

4 算例分析

本文所建立的模型为二阶锥优化模型,在AMPL 平台上编写相应程序并调用CPLEX 求解器求解。实验PC 机的CPU 为Intel（R）Core（TM）i7-10700,主频为2.90 GHz,内存为16 GB。

4.1 算例数据及场景设置

采用文献［16］中的园区IES 算例对所提模型进行验证。设备的相关参数和阶梯碳交易参数的数据分别详见附录A 表A1 和表A2,园区IES 包括3 类用户,其电、热和冷需求详见文献［17］。园区IES外购的热能价格、天然气价格和购水价格分别为0.19 元/（kW∙h）、1.8 元/（kW∙h）和4.1 元/t。弃风弃光惩罚系数为最低外购电价,即0.17 元/（kW ∙h）,IDR 成本系数取响应时段的电价,风电、光伏的预测数据来自文献［16］。

为验证本文所提的园区IES 低碳经济调度模型的有效性,本文设置以下3 个场景进行对比说明:

场景1:不计及IDR,根据系统用户初始的用能需求进行优化调度；

场景2:考虑IDR 且用户响应程度为1 的确定性优化调度模型；

场景3:考虑IDR 且用户响应程度为不确定性因素,求解本文提出的分布鲁棒优化调度模型。

4.2 优化结果对比与分析

不同场景中园区IES 的运行成本如表1 所示。由表1 可知,场景1 中园区IES 的运行成本最高,这是由于场景1 未考虑用户的IDR,虽然园区IES 运营商无须向用户支付IDR 成本,但是园区IES 出现大量的弃风弃光,系统碳交易成本高达3 681.97 元。与场景1 相比,在场景2 中,用户参与需求响应,虽然园区IES 运营商需要支付676.1 元的IDR 费用,但系统的弃风弃光有所缓解,系统购能、用水成本和碳交易均有所下降,总成本降低了18.55%。与场景2相比,场景3 考虑了用户需求响应的不确定性,IDR费用降低了11.84%,但其购能成本、用水成本、弃风弃光和碳交易成本均有所增加,总成本增加了1.6%,这是由于在部分时段用户未能完全按照预期响应量参与需求响应。

表1 不同场景中园区IES 的运行成本Table 1 Operation cost of park-level IES in different scenarios

为说明本文提出方法的有效性,将本文方法与Benders 分解方法和C&CG 方法进行比较。其中,两种迭代算法的最大迭代次数设置为100 次,比较结果如表2 所示。由表2 可知,采用Benders 分解方法和C&CG 方法所需时间分别为采用本文方法所需时间的27.97 倍和21.15 倍,验证了本文所提方法在求解效率上的优势。

表2 本文方法与Benders 分解方法和C&CG 方法比较Table 2 Comparison of the proposed method with Benders decomposition method and C&CG method

为进一步验证所提出的低碳经济调度优化模型的有效性,分析不同场景中用户参与需求响应后的电负荷和电价,其在典型日的变化曲线分别如图3和附录A 图A3 所示。选取1～7 和17～21 两个典型时段,对不同场景的优化结果进行分析。由图3 和附录A 图A3 可知,在时段1～7,与场景1 相比,场景2 和3 中最优电价有所降低且电负荷有所增加,这是因为在时段1～7,园区IES 电负荷需求较小,为提高风光消纳量,需通过降低电价引导用户增加电负荷,进而减少弃风弃光量。在时段15～21,与场景1 相比,场景2 和3 中最优电价有所增加且电负荷有所降低,这是因为该时段园区IES 用能需求大,通过提高电价引导用户减少其用电需求。与场景2 相比,场景3 中各时段电价的调整量均较小,这是因为在场景3 中考虑了用户IDR 程度的不确定性,优化结果需要满足鲁棒性的要求。

图3 不同场景中的电负荷曲线Fig.3 Curves of electric load in different scenarios

4.3 IDR 模型的有效性

为进一步验证本文所提基于用户用能习惯的IDR 模型的有效性,将所提出的IDR 模型与文献［42］的IDR 模型进行对比,并采用文献［43］提出的用户综合满意度作为评估指标。

求解不同IDR 模型得到的用户综合满意度曲线如图4 所示。

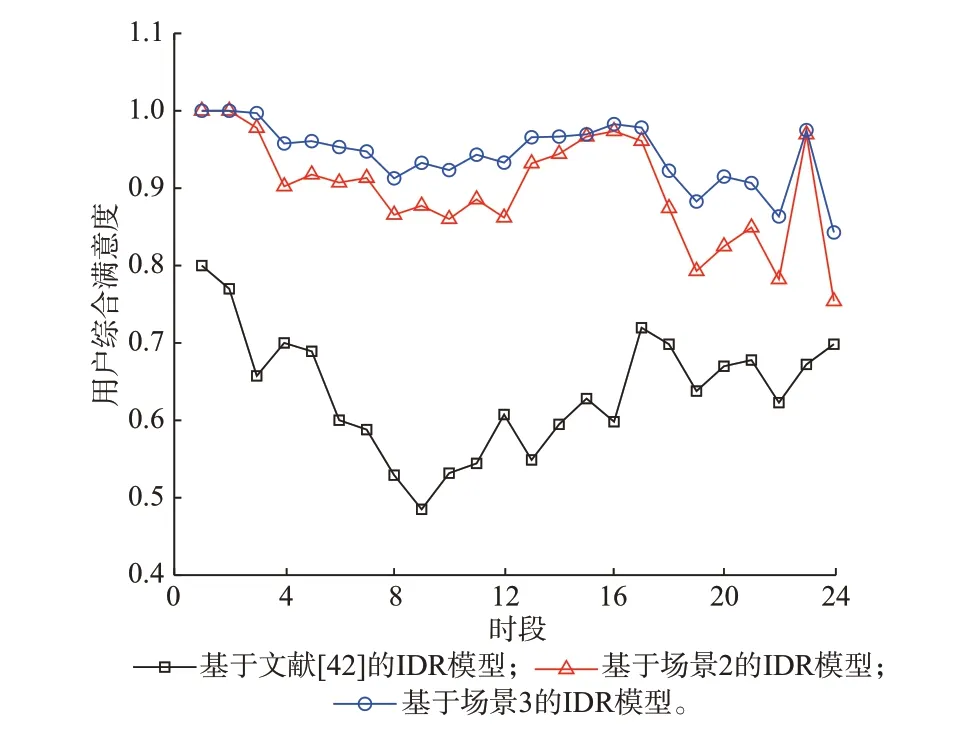
图4 求解不同需求响应模型得到的用户综合满意度曲线Fig.4 Curves of comprehensive satisfaction degree of customers obtained by solving different IDR models

由图4 可以看出,求解本文的IDR 模型（场景2和3）得到的用户综合满意度远大于求解文献［42］的IDR 模型得到的用户综合满意度。这是因为文献［42］仅约束楼宇冷、热负荷的温度位于舒适区间,与电负荷联系相对割裂,在多个时段出现同时削减电负荷和冷、热负荷的情况,导致用户的综合满意度较低且波动范围较大。本文所构建的IDR 模型是基于用户用能的历史数据,且电负荷的变化量和冷、热负荷的变化量相反,能够有效维持用户的用能习惯。例如,在场景2 中削减的电负荷为2 197.49 kW·h,然而补偿用户的冷、热负荷为1 201.84 kW·h。由于场景3 考虑了IDR 的不确定性,用户的综合满意度较场景2 更高,且波动更小,这是因为在考虑用户响应程度不确定性的情形下用户的需求响应量较小,调度方案更保守。

4.4 考虑燃料掺氢两阶段P2G 模型的有效性

为验证本文提出的考虑燃料掺氢的两阶段P2G 模型对减少园区IES 运行成本的积极作用,分别求解本文模型和文献［28］的两阶段P2G 模型,得到的系统运行成本对比结果如表3 所示。由表3 可以看出,采用本文提出的考虑燃料掺氢的两阶段P2G 模型求解得到的购气成本、弃风弃光惩罚费用和碳交易成本均小于求解文献［28］的模型得到的费用,且总运行成本降低了4.9%。

表3 求解本文模型和文献[28]的两阶段P2G 模型得到的系统运行成本对比Table 3 Comparison of system operation cost obtained by solving model proposed in this paper and two-stage P2G model proposed in reference [28]

附录A 图A4 展示了求解本文模型和文献［28］的两阶段P2G 模型得到的可再生能源消纳能力和燃气能量。附录A 图A5 展示了不同时段可再生能源预测出力和P2G 设备的掺氢比例。由图A4 可知,在分别求解考虑燃料掺氢和文献［28］的两阶段P2G 模型得到的调度方案中,园区IES 的可再生能源 消 纳 量 分 别 为3 754.82 kW ∙h 和3 629.41 kW ∙h。因此,在P2G 模型中考虑燃料掺氢有助于提高可再生能源消纳能力,进而降低弃风弃光惩罚费用和碳交易成本。求解本文模型得到的掺氢燃气能量大于求解文献［28］的两阶段P2G 模型得到的天然气能量,且由图A5 可知,不同时段P2G 设备掺氢比例与可再生能源预测出力的变化趋势相反。这是因为在风光预测出力小的时段,园区IES 对外购的天然气需求量较大,提高掺氢比例有助于减少P2G 设备中生产甲烷导致的能量损失,进而降低系统运行成本；在风光预测出力大的时段,系统外购能源的需求较小,减小掺氢比例可使更多的氢能与园区排放的碳产生化学反应生产甲烷,有助于降低系统碳排放,进而降低运行成本。

4.5 园区IES 运行风险分析

可再生能源出力、系统用户负荷需求和IDR 程度等因素的不确定性都会给园区IES 的经济运行带来风险。在市场环境下,当外部能源网络可提供的能量有限时,园区IES 的购能余额即购能上限与实际购能的差值,可作为衡量系统运行风险的重要依据［44］。

图5 展示了基于场景2 和3 得到的购电购热余额。由图5 可知,在场景2 的优化方案中,时段13～17 的购电余额为0,且时段9～15 和时段17～19 的购热余额为0。然而,场景3 的优化结果在对应时段均有一定的购能余额,其原因在于场景2 中对用户的响应意愿评估过于乐观,导致部分时段购能余额为0,系统功率平衡约束可能无法满足,进而增加了园区IES 的运行风险。场景3 中的鲁棒优化方案则可以在用户响应程度不确定的情况下兼顾园区IES调度方案的经济性和运行风险。

图5 场景2 和3 得到的购电和购热余额Fig.5 Spare electricity and heat available for purchase in scenarios 2 and 3

附录A 图A6 展示了用户响应程度的一阶矩μ和二阶矩η对园区IES 总购电余额的影响。由附录B 图B4 可知,随着二阶矩参数η的增大,园区IES的总购电余额呈减小的趋势,这是因为随着响应程度波动的增加,为保证优化方案的鲁棒性,园区IES的购能量有所增加,导致总购能余额减少。随着一阶矩参数μ的增大,园区IES 的总购电余额也会增加,这是因为当用户参与IDR 的意愿上升时,系统的电负荷和冷、热负荷的响应量增大,进而导致总购电余额有所增加。

5 结语

本文提出一种考虑用户响应不确定性和含燃料掺氢的P2G 设备运行特性的园区IES 日前低碳经济调度模型,并将其构建为基于混合整数二阶锥的分布鲁棒优化模型。通过算例分析得到如下结论:

1）利用所构建的基于园区用户的用能习惯的IDR 模型,系统运营机构可通过调整电价引导用户调整用能需求,在提高园区IES 经济性的同时,兼顾用户的用能满意度。

2）所提出的考虑燃料掺氢的两阶段P2G 模型能够通过调整掺氢比例适应可再生能源机组出力的波动,有效提升园区IES 消纳可再生能源发电的能力,并降低外购能源的需求以支撑其低碳经济运行。

3）所构建的基于分布鲁棒优化理论的园区IES日前低碳经济调度模型,能够增加购能余额从而降低系统运行风险。用户响应程度期望的降低和波动程度的增加均会提高系统运行风险,根据不同类型用户的用能习惯制定相应的需求响应方案,对园区IES 的安全经济运行具有重要意义。

本文所考虑的IDR 模型并未涉及天然气负荷,且所构建的园区IES 调度策略未考虑可再生能源出力的不确定性。研究含天然气负荷需求的IDR 模型以及可再生能源出力的不确定性对系统低碳调度策略的影响将是下一阶段的研究重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。