高比例新能源下的交直流配电网预测辅助区间状态估计

黄蔓云，费有蝶，卫志农，郑玉平，孙国强，臧海祥

（1.河海大学能源与电气学院,江苏省南京市 211100；2.南瑞集团有限公司（国网电力科学研究院有限公司）,江苏省南京市 211106）

0 引言

随着越来越多的新能源以分布式电源（distributed generator,DG）的形式接入配电网以及电动汽车等直流负荷比重的不断提高［1-2］,传统配电网正逐步转变为多能源供电的交直流主动配电网［3-5］。然而,间歇性DG 和柔性负荷的增多会加剧节点电压的波动,易导致电压越限、电能质量降低等问题［6-7］。因此,运用状态估计（state estimation,SE）技术［8-9］实时感知交直流配电网的当前运行状态,预知未来电压变化趋势,对保障交直流配电网的安全稳定运行具有重要意义。

由于配电网实时量测较少,需要大量基于历史数据或预测得到的伪量测（如DG 出力数据、负荷功率）保证全网的可观测性［10］。但伪量测的误差难以保证,其具体的概率分布更是难以准确获取,这将导致加权最小二乘（weighted least square,WLS）法等点估计方法精度下降。为解决此问题,在配电网SE中需要考虑不确定变量的影响。常用方法主要包括概率模型［11］、模糊数模型［12］和区间模型［13］。前两者模型需要预先获取所需的概率密度函数或隶属度函数,而区间模型仅需变量的上下界信息,不需要特定的分布,在实际应用中具有更强的适用性。

目前,区间SE 或潮流计算的方法主要包括以下几类。1）区间约束传播法［14-16］:利用区间运算迭代收缩状态的取值范围,但其忽略了同一变量在不同约束中的相关性,保守性较高。2）基于Krawczyk算子的方法（以下简称Krawczyk 算法）［17-18］:利用相量测量单元（phasor measurement unit,PMU）和数据采集与监控（supervisory control and data acquisition,SCADA）系统的混合量测,通过量测变换建立线性方程组进行求解,但量测变换过程中会扩张量测区间,并且配电网的低量测覆盖率和PMU的高配置成本降低了该方法在大多数配电网中的工程实用性。3）仿射算法［19-21］:将不确定变量用仿射数表示进行计算,然而仿射的非线性运算较为复杂,引入的新噪声元会导致区间扩张,计算结果较为保守。4）优化法［22-24］:非线性优化模型非凸,无法保证解的完备性,相关的线性化方法或依赖于区间中值的准确性,或无法快速确定准确的初始迭代区间。随着直流配电网的发展,不确定性分析的研究对象逐渐从单一交流配电网转向交直流混合配电网［25-27］,但交直流区间SE 主要是使用已有的非线性优化模型,鲜有改进。

针对交直流配电网中DG 出力波动、量测冗余度低、三相不平衡等特点,本文构建了一种基于状态预测的交直流配电网线性区间SE 模型。设计了一种含辨识修正环节的状态区间预测方法以缩小状态搜索空间,提高区间SE 的计算效率。放缩非线性约束方程,在无需量测变换的情况下,将非线性优化模型转化为线性优化模型,保证了区间估计结果的完备性和可靠性,仿真验证了本文方法的可行性和准确性。

1 交直流配电网区间SE

不同于传统交流配电网区间SE 模型,交直流配电网区间SE 模型在状态变量、量测模型和潮流约束方面均有所扩充。状态变量方面,引入了直流配电网和电压源换流器（voltage source converter,VSC）出口的状态量；量测模型方面,增加了直流配电网和DG 的量测方程；潮流约束方面,计及了VSC的控制方式和交、直流配电网的功率耦合关系。

1.1 换流器等效模型

直流配电网和大部分DG 需要通过电力电子换流器才能接入交流配电网。其中,电压源换流器应用最为广泛,VSC 的潮流模型如图1 所示。图中:i为连有VSC 入口交流节点的编号；j为VSC 出口交流节点的编号；d为VSC 的直流节点的编号；rij,a和xij,a分别为VSC 支路ij中a 相的等效电阻和电抗；rij,b和xij,b分别为VSC 支路ij中b 相的等效电阻和电抗；rij,c和xij,c分别为VSC 支路ij中c 相的等效电阻和电抗；Pvsc,d和Pvsc,j分别为VSC 直流侧节点d和交流侧节点j的有功功率,以图中箭头方向为正方向；Pvsc,loss为换流器的有功损耗。

图1 换流器模型Fig.1 Converter model

以直角坐标形式表示电压和电流,VSC 交直流两侧的功率平衡关系为:

式中:Ure,j,φ和Uim,j,φ分别为节点j的φ相电压的实部和虚部；Ire,ij,φ和Iim,ij,φ分别为VSC 支路ij的φ相电流的 实 部 和 虚 部；Ivsc,φ为VSC 支 路φ相 电 流 的 幅 值；η1、η2和η3为VSC 的功率损耗系数。

假设VSC 结构三相对称,阻抗相间无耦合［28］,则有rij,φ+jxij,φ=rij,ϕ+jxij,ϕ（φ,ϕ∈{a,b,c}）,其中,rij,φ和xij,φ分 别 为VSC 支 路ij中φ相 的 等 效 电 阻 和 电抗,rij,ϕ和xij,ϕ分 别 为VSC 支 路ij中ϕ相 的 等 效 电 阻和电抗。此外,VSC接入交流配电网时可进行三相不平衡补偿,使其端口电压三相对称［29］,表达式如式（4）所示。

1.2 交直流配电网状态变量

区间SE 中,量测向量z和状态向量x都以区间数的形式出现,即处在已知的上下限之内:

式中:inv(⋅)为区间数；和分别为量测向量的上、下限；和分别为状态向量的上、下限。为了表述方便,本文的量测量和状态变量均省略了区间数的形式。

本文选取的状态向量为:

式中:Ure和Uim分别为交流节点电压的实部和虚部向量；Ire和Iim分别为交流支路电流的实部和虚部向量；Ivsc为VSC 支路电流幅值向量；Udc为直流节点电压幅值向量。

由于增加了状态变量的维数,需要增加有关状态变量的方程保证系统可观:

式中:rij,φϕ和xij,φϕ分别为交流支路ij中φ相和ϕ相间的 电 阻 和 电 抗；Ire,ij,ϕ和Iim,ij,ϕ分 别 为 交 流 支 路ij中ϕ相电流的实部和虚部。

1.3 交直流配电网量测方程

1.3.1 交流和直流配电网量测方程

交流配电网的量测量为电压幅值、支路电流幅值、节点注入有功功率和无功功率。其中,电压幅值转换为电压幅值的平方,支路电流幅值转换为支路电流幅值的平方,转换后的量测满足误差传递规律。由于状态量和量测量均为区间变量。因此,量测方程中可以不考虑误差项。量测方程的具体形式为:

式 中:Vac,m,i,φ为 交 流 节 点i的φ相 电 压 幅 值 的 平 方；Lac,m,ij,φ为 交 流 支 路ij的φ相 电 流 幅 值 的 平 方；Pac,m,i,φ和Qac,m,i,φ分 别 为 交 流 节 点i的φ相 注 入 的 有功功率和无功功率；Nac,i为与节点i相连的交流节点集合。

直流配电网的量测量为节点电压幅值、支路电流幅值和节点注入功率。量测方程的具体形式为:

式中:Udc,m,μ为直流节点μ的注入电压；Udc,μη为节点μ和 节 点η之 前 的 直 流 支 路 的 电 压；Idc,m,μη为 直 流 支路μη的 电 流；Udc,μ为 直 流 节 点μ的 电 压；gdc,μη为 节点μ和 节 点η之 前 的 直 流 支 路 电 导；Pdc,m,μ为 注 入 直流 节 点μ的 有 功 功 率；Gdc,μη为 直 流 配 电 网 节 点 导 纳矩阵中的对应元素；Ndc,μ为与节点μ相连的直流节点集合；NVSC,μ为与节点μ相连的VSC 集合。

1.3.2 换流器控制变量方程及DG 出力方程

对于与直流配电网相连的VSC,本文考虑主从控制模式,将一台换流站作为主换流站维持直流侧节点电压稳定,其余换流站的控制方式采用交流侧并网有功功率和无功类变量（交流并网侧电压或交流并网侧无功功率）的组合。作为交直流配电网中的关键设施,换流站的控制信息需要及时传达至调度中心,并且其控制目标值接近于实际值。因此,VSC 的控制信息在交直流配电网的不确定性分析中可作为确定性信息提高系统的可观测性。

根据VSC 的控制方式,约束方程为:

式中:Udc,d为VSC 直流侧节点d的电压幅值；Uset,d为VSC 直流侧节点d的电压设定值；Pin,set和Qin,set分别为VSC 通过交流并网节点流入交流配电网的三相总有功和无功功率的设定值；Uset,i为VSC 对并网节点i正序电压的设定值。

DG 的并网方式有经换流器并网和直接并网［30］。两种方式的等效模型均有支路参数三相对称、端口电压三相对称的特点。DG 出力为从并网点流入配电网的三相总功率。因此,两种并网方式下DG 出力的量测方程相同。假设DG 出力由预测方法获得,由于难以精准预测瞬时风速、太阳辐射等天气因素,预测获得的伪量测误差远大于实时量测误差。量测方程为:

式中:Pin,DG、Qin,DG分别为DG 有功和无功出力的量测量。

1.4 区间SE 模型

区间SE 基于误差未知但有界理论,将量测集合映射到状态集合,状态真值则被界定在状态集合中。因此,估计结果具有较高的可信性。利用区间数,量测方程可以统一表示为:

式中:h(⋅)为状态向量和量测向量之间的函数关系。

量测向量z和状态向量x的每一分量均为区间数,可以看出,用区间数表示量测值,消除了对量测误差概率分布的假设。

求出每个状态变量的上下界即可求得状态区间为[minxτ,maxxτ],其中xτ为状态向量x的第τ个分量。因此,可建立模型为:

将量测系统提供的量测区间作为量测估计值的初始区间,当完整考虑所有约束方程时,量测估计值的区间与初始区间相比,范围可能会缩小。因此,以每个量测估计值变量作为目标函数,可获得量测估计值新的上下界:

2 区间SE 的线性化求解方法

原始的非线性优化模型（式（25）和式（26））综合考虑了量测上下界约束、零注入功率约束、状态变量的关系约束以及换流器的控制约束,但由于该模型是非凸的,无法保证获得全局最优解。为了提高结果的完备性,本文将原优化模型转化为线性优化模型,并采用迭代计算的方式,不断缩小状态变量和量测变量的区间以降低估计结果的保守性。

2.1 约束方程的线性化

同理,区间SE 模型中的其余非线性约束方程都可以转化为相应的两个线性不等式,最终实现区间估计模型的线性化。值得一提的是,采用直角坐标下的节点电压、支路电流以及VSC 支路电流幅值作为交流配电网的状态变量,虽然增加了式（8）至式（10）的约束,但简化了交流约束方程的偏导函数,以及式（1）至式（3）和式（17）组成的VSC 直流侧节点注入功率方程的偏导数。因此的求解较为简便,降低了线性化过程的计算复杂度。

2.2 区间SE 求解模型

利用2.1 节的方法将区间SE 的原始非线性求解模型转化为:

由于对非线性等式进行了放缩,单次求解得到的区间具有较高的保守性,因此需要进行迭代求解,具体步骤如下:

步骤1:设置状态变量的初始区间x0,根据量测系统提供的量测区间获得量测量的初始区间z0。

步骤2:设置迭代次数l=1。

步骤3:求解式（34）获得状态量区间xl和量测量区间zl。

步骤 4:比较区间数向量 [xl,zl]T和[xl-1,zl-1]T,若区间宽度的最大差值小于收敛门槛值ε,则停止迭代,否则转至步骤5。

3 预测辅助的区间估计算法

在网络结构和线路参数不变的情况下,交直流配电网的运行状态受到负荷功率和DG 输出功率的影响。一方面,从长期来看,系统状态的变化具有一定的规律性,本文将两参数指数平滑法改成区间形式,拟合状态的变化趋势；另一方面,在较短的时间段内,系统状态会因负荷和DG 功率的随机波动而波动,可能导致预测区间不准（不包含真值）,本文设计一种预测区间修正方法,辨识并修正不准确的预测区间,进而辅助提高区间SE 结果的可靠性。

根据区间数的数学运算规则［20］,用区间数表示两参数指数平滑法的形式为:

若预测区间不准确,则估计区间必然不包含状态真值,并且可能导致区间SE 的解为空集。在此情况下,本文采用如下修正方案。

3）若xk+1,opt的 某 一 分 量 区 间xk+1,opt,τ未 被 完 全包 含 在对 应 的 分 量中,则 判 断为不准确的预测区间,按此原则辨识出中所有不准的预测区间,其对应的状态集合设为Np。

4）以xk+1,opt中 集 合Np的 状 态 区 间xk+1,opt,Np的中点为中心点,以先前各时间断面集合Np的预测区间的平均宽度为区间宽度,重新生成预测区间,代替原区间。

需要说明的是,在量测误差区间包含真值的前提下,虽然非线性模型式（25）的解是激进的、不全面的,但其求解出的区间xk+1,opt是满足所有约束的可行解,并且包含真值［24］。因此,不能完全覆盖xk+1,opt的预测区间可能是不准确的。虽然步骤3 可能会将准确的预测区间辨识为不准,但修正后的区间是准确的,对区间SE 结果的可靠性没有影响,具体测试效果见第4.1 节。将状态的预测区间作为初始区间,基于2.2 节的区间SE 算法对初始区间进行收缩。与根据主观经验设置的初始区间相比,预测区间的保守性更低,有助于减少后续区间SE 的迭代次数,加快收敛速度。本文算法在第k+1 个时段的计算流程如图2 所示。

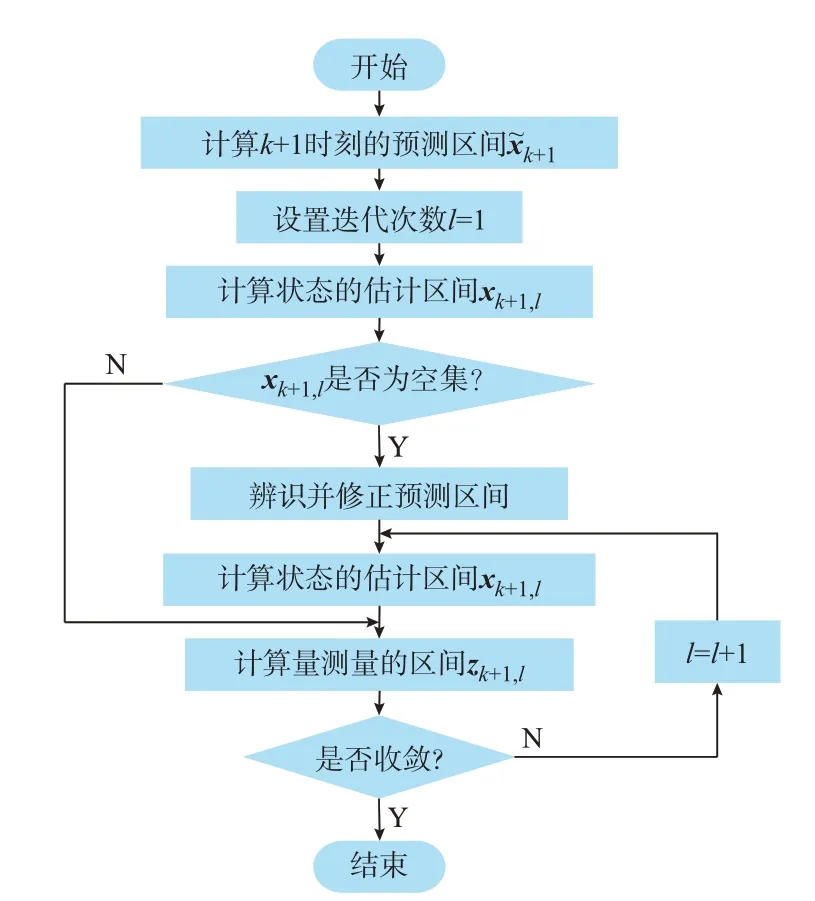
图2 第k+1 个时段算法流程图Fig.2 Flow chart of the proposed algorithm during the(k+1)thtime period

4 算例分析

为验证本文算法的估计效果,将三相不平衡的IEEE 33 节点系统拓展成交直流配电网作为本文的测试系统,系统结构如附录A 图A1 所示,测试系统的线路参数和负荷参数来自文献［31］。其中,交流配电网的基准电压为12.66 kV,直流配电网的基准电压为10 kV,基准容量均为10 MV·A。VSC 的参数及控制方式如表A1 所示。交流配电网中,DG 均通过换流器并网,其中,DG3 为风力发电系统,其余为光伏发电系统,并网参数如表A2 所示。直流配电网的DG 为光伏发电系统,额定容量为400 kW。量测值是在潮流真值的基础上添加随机噪声得到的,实时量测（电压幅值、支路电流幅值、部分节点注入功率）的最大误差为5%；负荷节点功率伪量测的最大误差为10%；DG 出力伪量测的最大误差为25%。量测配置信息如表A3 所示,各量测类型的数目为三相总数。

4.1 估计效果测试

根据负荷曲线和DG 出力曲线,以15 min为间隔,进行连续100 个时间断面的测试,在每个时间断面使用基于WLS 法的点估计和基于本文算法的区间SE。其中,WLS法的输入为服从正态分布的量测点值向量zmea,标准差向量为σ；区间SE 的输入是以zmea±3σ边界的量测向量区间。采用平均估计误差和最大估计误差衡量 WLS 法的估计精度,表达式为:

式中:Eavg和Emax分别为平均估计误差和最大估计误 差；N为 时 间 断 面 数；n为 状 态 变 量 数；xestk,τ为第k个 时 段 第τ个 状 态 变 量 的 估 计 值；xtruek,τ为 第k个时段第τ个状态变量的真值。

对于区间SE,采用真值覆盖率衡量其可靠性,采用平均区间宽度和最大区间宽度衡量其保守性,各指标的计算式为:

式 中:C为 真 值 覆 盖 率；ck,τ为 第k个 时 段 第τ个 状 态区 间 是 否 包 含 其 真 值 的0-1 变 量和-xk,τ分 别 为第k个 时 段 第τ个 状 态 变 量 的 上、下 限,若≤xtruek,τ≤,则ck,τ=1,否则ck,τ=0；Wavg和Wmax分别为平均区间宽度和最大区间宽度。

测试结果如表1 所示。显然,本文所提出的预测辅助区间状态估计（forecast aided interval state estimation,FAISE）算法具有较高的可靠性,并且估计区间的保守性较低。

表1 WLS 法和FAISE 算法的估计结果Table 1 Estimation results of WLS method and FAISE algorithm

由表1 可知,相比于FAISE 算法,WLS 法估计结果的准确性较低,这是由于WLS法的优化目标是量测估计值与量测值较为接近,而这并不能保证SE值与状态真值较为接近。此外,WLS法在计算过程中不考虑量测误差的范围为-3σ～+3σ,这可能导致由WLS法的SE 值所计算出的量测估计向量不满足zmea-3σ≤≤zmea+3σ,影 响 估 计 结 果 的 准 确 性。而FAISE 算法在求解过程中利用约束条件限制了量测估计值必须满足zmea-3σ≤≤zmea+3σ。

在某一时段,使用蒙特卡洛模拟（Monte Carlo simulation,MCS）法［32］进 行10 000 次 抽 样,与FAISE 算法的对比如图3 所示。由图3 可知,MCS法的保守性过高,这是由于MCS 法获得的状态集合是WLS 法点估计值的组合,其中包含了不符合量测约束的状态运行点。

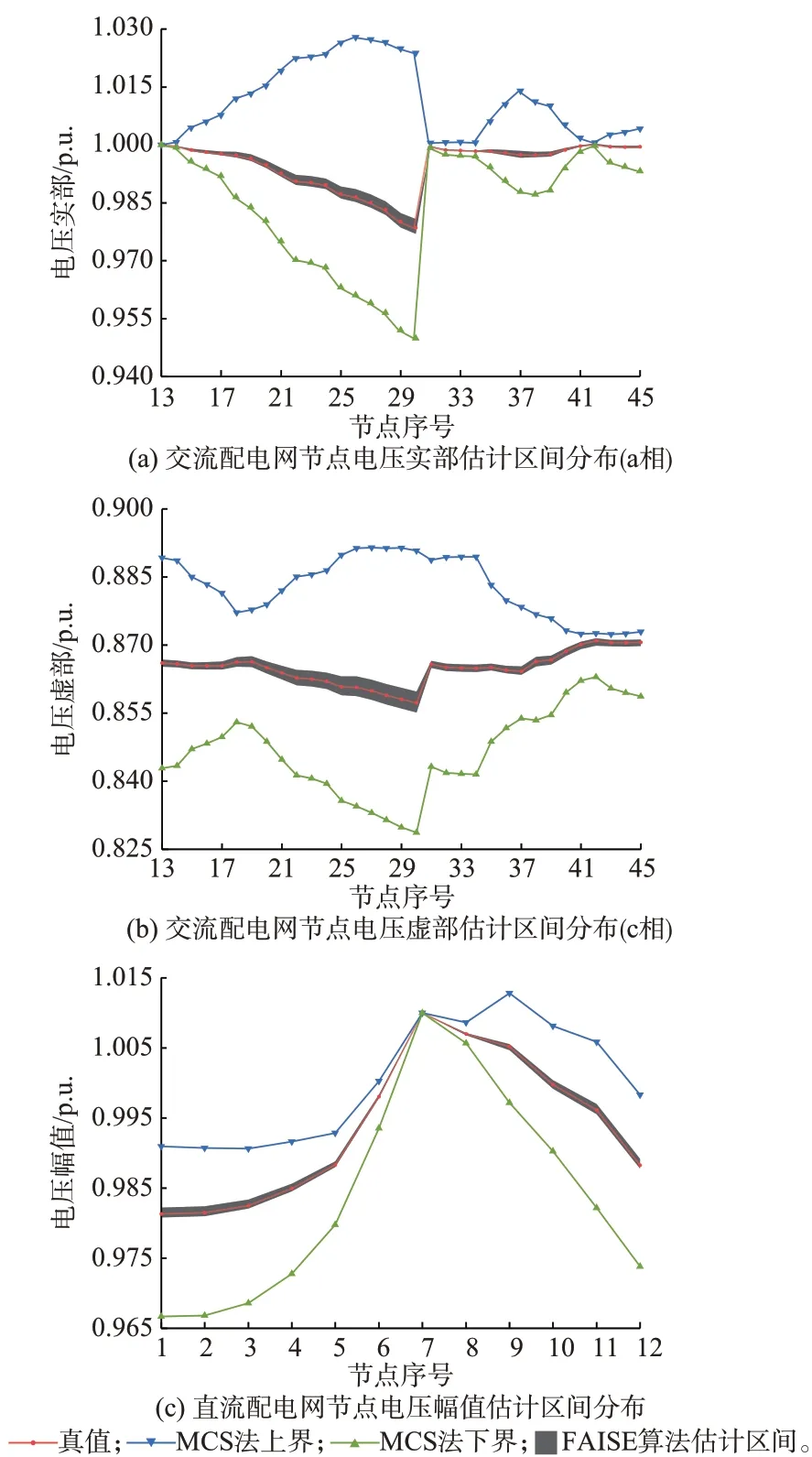
图3 MCS 法和FAISE 算法的估计区间Fig.3 Estimation intervals of MCS method and FAISE algorithm

4.2 与Krawczyk 算法的线性化区间SE 对比测试

为验证本文所提线性化模型的有效性,将本文算 法 与Krawczyk 算 法 的 线 性 区 间SE［17,33］进 行 对比。Krawczyk 算法的区间SE 是将量测量转换为电压实部、虚部或电流实部、虚部量测以线性化量测方程。需要指出的是,由于VSC 的损耗和DG 注入交流配电网功率的三相不平衡,式（1）、式（21）以及VSC 和DG 关于三相功率和的量测方程难以通过量测转换的方法线性化,而本文的线性化方法不需要量测转换,能够适用于上述方程。

为了在相同的条件下对两种算法进行客观比较,本小节对交流和直流配电网分别进行区间估计,并使两种区间估计器的输入量测相同。两种算法估计结果的相应指标如表2 所示。显然,FAISE 算法相比于Krawczyk 算法估计区间更窄、保守性更低,估计结果的可靠性更高。可以预见,若在FAISE 算法中增加Krawczyk 算法无法线性化的量测,估计区间的保守性会进一步降低,说明本文所提的线性化模型具有一定的优越性。

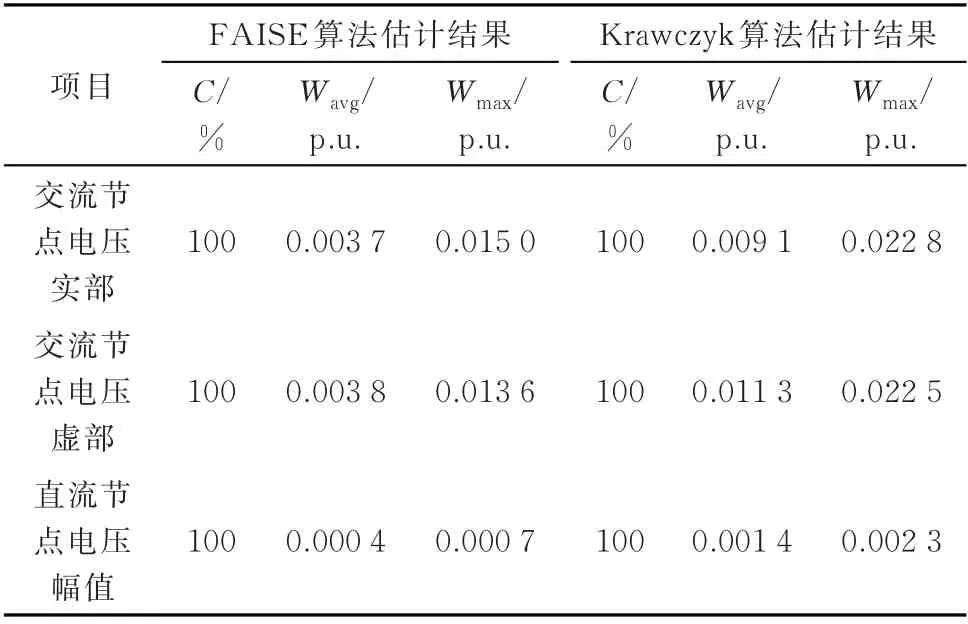
表2 FAISE 算法和Krawczyk 算法的估计结果Table 2 Estimation result of FAISE method and Krawczyk algorithm

为了对两种算法进行更加直观的对比,图4 给出了交流配电网部分状态量和直流配电网状态量的估计区间。由图4 可知出,在任一节点处,FAISE 算法求解出的区间范围均小于Krawczyk 算法求解出的区间范围。通过分析可知,由于FAISE 算法在每一次迭代中同时求解量测量和状态量的区间,而量测区间的缩小有助于进一步缩小状态区间,FAISE算法可以有效缓解不确定状态区间的保守性。

图4 交流和直流配电网中FAISE 算法和Krawczyk 算法的估计区间Fig.4 Estimation intervals of FAISE method and Krawczyk algorithm in AC and DC distribution networks

4.3 收敛性能和计算效率

由于配电网实时量测主要以支路电流为主［16］,本节改变交流配电网支路电流幅值实时量测的数量,研究本文算法的收敛性能。需要说明的是,利用式（34）求解交直流配电网状态量和量测量的上下界时,虽然目标函数不同,但约束相同。因此,每次迭代中的线性优化模型可以并行求解。设阈值ε=10-4,图5 显示了在不同实时量测配置下,交流节点电压实部的平均区间宽度在迭代过程中的变化。由图5 可知,支路电流量测的数量越少,迭代次数越少,但最终的估计区间宽度较大。当电流量测数量增加到15×3 个后,估计区间平均宽度的减小幅度很小,而迭代次数却逐渐增多,说明不需要大量配置支路电流实时量测。对于本文算例,配置数量为15×3 个时能够以较少的迭代次数获得较窄的估计区间。

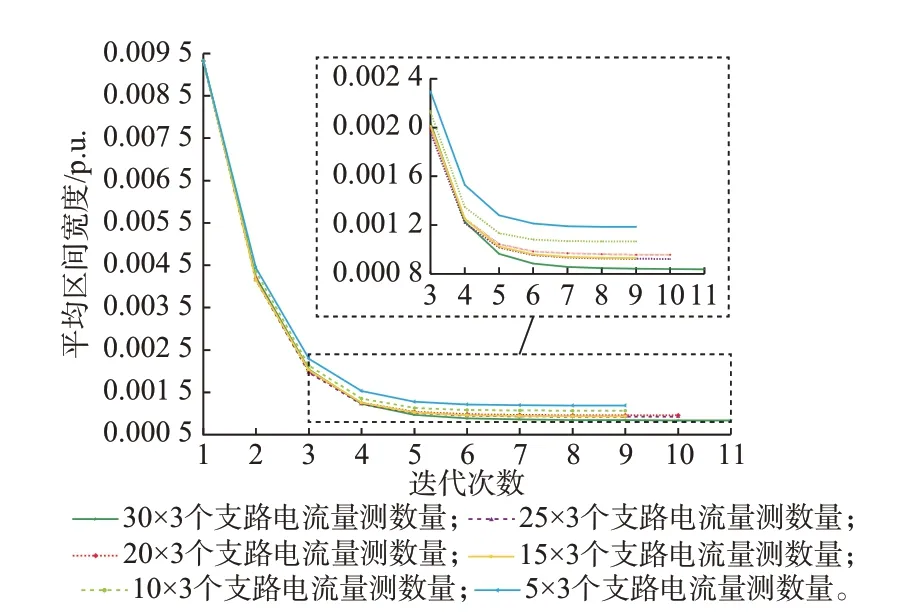
图5 交流节点电压实部的平均区间宽度在不同支路电流量测配置下的变化过程Fig.5 Variation process of average interval width of real part of AC node voltage with different branch current measurement configurations

图5 中各量测配置下的计算时间如表3 所示。由表3 可知,本文算法的计算时间小于3 s,能够满足配电网SE 的要求。

表3 不同量测配置下的迭代次数和计算时间Table 3 Numbers of iterations and computation time with different measurement configurations

5 结语

本文主要工作如下:

1）为计及DG 出力的间歇性、量测误差的不确定性对交直流配电网SE 的影响,本文采用区间描述不确定变量,建立了交直流配电网的区间SE 模型,该模型能够考虑系统的三相不平衡问题,避免了对DG 出力和量测误差的分布进行假设。

2）为解决原始区间SE 模型非凸而难以获得全局最优解的问题,本文在无需量测变换的情况下将非线性约束转化为线性约束,通过迭代缩小状态量和量测量的区间。算例测试表明,所提方法既能保证SE 解的可靠性,也能有效降低估计区间的保守性。

3）为提前获取电压波动信息,为区间SE 提供可靠的初始区间,本文基于指数平滑法设计了一种状态区间预测方法。该方法能在状态变化平缓时准确预测状态区间,在状态突变时辨识并修正预测区间,为区间SE 的有效应用提供了前提和保证。

今后,可在此基础上进一步研究分布式区间估计技术提高计算效率,研究关于量测区间的坏数据辨识技术提高区间估计器的鲁棒性,计及VSC 控制方式的切换以及更多的运行约束提高区间SE 的在线应用能力。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。