基于纵向联邦学习的短期风电功率协同预测方法

赵寒亭，张 耀，霍 巍，王建学，吴 峰，张 衡

（1.西安交通大学电气工程学院,陕西省西安市 710049；2.大航有能电气有限公司,江苏省扬中市 212211）

0 引言

风电对改善能源结构及减少温室气体排放的意义重大,但风电功率的波动性、间歇性和随机性却会对电力系统的可靠性及电能质量造成不可忽视的影响［1］。开发一种先进的风电功率预测方法,以提高风电功率的预测精度是减少风电波动性、间歇性和随机性对电力系统运行影响,增强电网消纳风电能力的一种较为有效的解决方案［2］。

近年来,国内外学者做了大量工作,开发了许多基于时间序列分析、机器学习和深度学习方法的风电功率预测模型。典型代表有支持向量机［3］、随机森 林［4］、XGBoost 模 型［4-5］、多 层 感 知 机（multi-layer perceptron,MLP）、门控循环单元（gated recurrent unit,GRU）以及长短期记忆（long short-term memory,LSTM）网络等模型［6］。根据风电预测终端用户的具体需求,以上方法既可以提供点预测结果,也可以提供区间预测结果。

为了进一步提高风电功率预测的准确性,近年来一些研究利用了风力资源具有时空相关性这一重要特征,将相邻风电场站的相关数据信息纳入待预测场站的风电功率预测模型之中,以此来进一步提高待预测场站的风电功率预测精度［7-13］。此类考虑时空相关性的风电功率预测研究主要集中在两个方面。一是分析和论证了同一地区的风电场站之间存在潜在的时空相关性,提出了针对性的建模预测方法［9-10］。二是证实和量化了利用相邻场站数据可以提高风电功率预测精度,特别是在具有特定主导风型和风向的地区,此效益将更为显著［11-12］。上述工作为合理利用风力资源的时空相关性、提高风电功率预测精度做出了重要贡献。

上述研究都是基于一个假设,即待预测场站可以完全获得邻近场站的相关数据信息。从技术上看,通过先进量测技术和通信技术,可以实现从邻近场站到待预测场站的数据采集和传输工作。然而在现实情况中,同一地区的不同场站可能分属不同的发电集团。由于商业竞争关系和数据安全方面的考量,不同发电集团之间通常并不愿意彼此交换数据,这阻碍了上述研究的推广应用。此外,传统的风电功率预测模型都是通过集中式训练来完成参数估计。当预测模型包含越来越多的相邻场站数据时,将会导致超大规模的预测模型估计问题。对于此类大规模预测模型而言,无论是数据的收集汇总,还是模型的参数估计,都将变得十分困难。

采用联邦学习机制来开发新型分布式预测方法,是应对上述挑战的一种可行思路。借助联邦学习机制,可以在保证各参与方数据隐私安全的基础上,间接利用其他邻近场站的相关数据,从而打破数据孤岛,实现多方协作、共同建立并训练预测模型的目标［14-15］,所提方法不仅可以提高待预测场站的风电功率预测精度,还可以提高预测模型的训练效率。

到目前为止,联邦学习主要从数据并行和模型并行两方面开发了机器学习算法的分布式实现方式［14-15］,在负荷预测和新能源预测等领域得到了有效应用。文献［16］基于长短期时间序列网络,提出了一种面向行业用户读表数据保护的联邦学习负荷预测框架。文献［17］提出了一种基于联邦学习的分布式训练框架,并利用该框架对电力计量数据进行分析。文献［18］基于深度学习、变分贝叶斯推断和联邦学习,提出了一种太阳辐照度概率预测模型。文献［19］提出了一种将联邦学习和深度强化学习相结合的预测方案,用于超短期风电功率预测。文献［20］基于LSTM 网络,提出了一种基于联邦学习机制的短期风电功率预测方法。上述研究表明将联邦学习方法应用在电力系统领域的可行性和实用性,但其具体思想还未广泛应用到风电功率预测之中。因此,基于联邦学习的风电功率分布式协同预测方法值得进一步开展研究。

1 基于改进岭回归的风电协调预测模型

1.1 预测模型的符号与定义

假设某个地区有L个风电场站,并用si表示该地区的风电场站,其中i=1,2,…,L,记该地区所有风电场站构成的集合为Ε,则有:

位于同一地区的各个风电场站分属不同的发电集团,假设共有G个发电集团,其中,第g个发电集团拥有Lg个风电场站,所构成的子集记为Eg,其中g=1,2,…,G,Eg的具体形式如下:

由上述有关定义可知:

在附录A 中,本文对上述的集合化关系定义进行了详细的举例说明。最后,本文对G个发电集团进行分类,具体如下:

1）待预测对象:指需要对其风电功率进行预测的发电集团,其索引记为ℓ,ℓ 可取1,2,…,G中的某一个值；

2）辅助合作者:指在联邦学习过程中,向待预测对象提供相关数据信息,帮助待预测对象提高预测精度的相邻其他发电集团。

需要注意的是,本文所提出的预测模型主要用于提升待预测对象的风电功率预测精度。如果需要提高某一辅助合作者的预测精度,则需要将该辅助合作者视为待预测对象,然后再应用本文方法。

1.2 基于岭回归的风电功率协同预测模型

假设在任意时刻t,待预测对象ℓ 的风电功率yℓ,t是各个输入特征的线性函数,如式（5）所示。式（5）的右侧项包含两类输入特征,第1 类是来自待预测对 象ℓ 的 本 地 输 入 特 征xℓ,t,第2 类 是 来 自G-1 个辅助合作者的离站输入特征xg,t(g≠ℓ)。

式中:xg,t∈Rng为发电集团g在t时刻的输入特征向量,其中ng为相应的向量维度的大小；θg∈Rng为发电集团g的拟合参数向量；ε(t)表示拟合误差。

在式（5）中,通过使用相邻场站的相关数据来更好地捕获风力资源的时空相关性及时空传播变化情况［12-13］,从 而 提 高 待 预 测 对 象ℓ 的 风 电 功 率 预 测精度。

为了消除输入特征之间的多重共线性现象,防止预测模型过拟合,提高预测模型的泛化能力,本文采用改进的最小二乘估计法,即岭回归模型［21］进行建模分析,进而求解出相应的拟合参数向量θg。给定M个历史样本,其对应的岭回归优化问题如下所示:

在实际应用时,各风电场站首先需要采用“前向选择”或“后向选择”算法进行输入特征筛选,挑选出有助于提升风电功率预测精度的输入特征集合,然后再参与联邦学习过程。关于选取岭回归模型的详细原因、式（5）和式（6）的详细推导过程以及xg,t、θg、的具体构造方法,均在附录B 中给出。

1.3 基于改进k近邻和深度学习方法的岭回归模型

1.2 节介绍的标准岭回归模型是一种全局的线性回归模型,然而风电预测中所使用的数据样本点在空间中通常呈现出非线性分布的特点。因此,在采用标准岭回归模型进行风电预测时,不一定能够很好地拟合所有的样本点,在实际应用中可能出现“欠拟合”现象,导致模型泛化能力不足、预测可靠性较差。针对上述问题,考虑从两方面对岭回归协同预测模型进行改进,具体如下。

1）改进措施1:将全局的非线性回归问题划分为若干个局部区域的线性回归问题,从而提升线性模型的拟合效果。其具体思路是首先,根据待预测样本点的特征属性,从训练集中筛选出属性相近的部分样本点,构成相应的子训练集；然后,使用子训练集来训练模型并得到相应的拟合系数；最后,对待预测样本点进行预测。

改进措施1 忽略了与待预测样本点距离较远的训练集样本,只使用待预测样本点局部邻域内的训练集样本进行模型的训练。对于不同的待预测样本点,所选出的子训练集往往是不同的,故训练得到的拟合系数也不同。这样便可以针对不同的待预测样本点作出相应的局部调整,从而改善欠拟合现象,提高预测精度。

由于k近邻（k-nearst neighbor,KNN）算法简单易行,在筛选相似样本时准确度较高且对异常值不敏感,本文使用KNN 算法对训练样本进行预筛选。

传统KNN 算法需要遍历计算待预测样本点与训练数据集中的每个历史样本点之间的距离,其计算量较大。为了提高KNN 算法的搜索效率,本文采用kd 树（k-dimensional tree）方法来实现对训练数据的快速KNN 搜索。kd 树的使用过程分为两个步骤；一是构造kd 树,即使用特殊的二叉树结构来存储训练数据；二是利用kd 树进行快速KNN 搜索,即根据待预测样本点的特征属性,搜索过程会被限制在训练集样本空间的局部区域上,省去了对其余大部分训练样本的搜索,大幅度地减少了欧氏距离的计算次数以及搜索时的计算量,可以显著提高计算效率。关于本文所采用的kd 树,其更多内容介绍请参考文献［22］。

2）改进措施2:在输入特征中增添非线性成分,以提升拟合效果,实现更精准的预测。其具体思路是让每个参与联邦学习的风电场站都预先采用学习能力和拟合能力更强的深度学习方法进行训练和预测；然后,再将其功率预测结果和输入特征纳入基于岭回归的风电功率协同预测模型之中,以此来进一步提升预测精度。

改进岭回归模型所对应的优化问题与式（6）的形式完全相同,如下所示:

式中:Xg∈Rm×ng和yℓ∈Rm为对应于待预测样本点的子训练集,其中Xg中包含了各场站原有的输入特征以及来自深度学习方法的功率预测结果,m为子训练集的样本数。

2 基于联邦学习的分布式训练与预测

2.1 联邦学习概述

联邦学习是一种分布式机器学习方法,解决了不同数据拥有方在不交换隐私数据的情况下进行联合建模和多方协作的问题。针对不同参与方的数据在样本空间和特征空间的重叠情况,主流研究一般将联邦学习分为“横向联邦学习”“纵向联邦学习”和“联邦迁移学习”［14］。其中,“纵向联邦学习”适用于各参与方的样本空间相同但特征空间不同的数据场景。

在本文的应用场景中,由于各发电集团均有各自在相同历史时间段的数据集,即各发电集团的数据集在时间范围上是重合的,故各发电集团的样本空间相同。由于不同发电集团的数据集主要采集的是来自不同地理位置的数值天气预报信息和风功率观测信息,属于不同的空间特征,故各发电集团的特征空间不相同。为了充分利用风力资源的时空相关性,本文所提方法希望在预测模型中考虑来自不同地理位置上的输入特征,通过“特征联合”（即纵向联邦学习）实现特征增强,最终提高预测精度。因此,本文所提方法属于“纵向联邦学习”。

在1.3 节中,给出了改进岭回归模型所对应的优化问题（式（7））。尽管风电场站为不同的发电集团所拥有,但它们可以通过相互合作来提高预测质量。为了保证各参与方的数据隐私安全,本文将借助纵向联邦学习机制,开发预测模型的相关优化算法,推导出优化问题（式（7））的迭代求解框架。在迭代框架下,依据求解最优模型的需要,对岭回归模型做纵向划分,将原本的大规模优化、预测问题分解为大量的小规模子问题,且每个子问题都可由相应的参与方在本地进行边缘计算。在此基础上,总结出改进岭回归模型的分布式训练过程和分布式预测过程,从而解决不同数据拥有方在不交换机密数据的情况下进行多方协作的问题。

在上述过程中,需要引入一个“中央协调者”,可以由政府部门或可信任的电网调度机构担任,负责监督和协调分布式训练及预测过程。下面分别介绍在联邦学习机制下,如何以分布式方式开展训练样本预筛选以及协同模型的训练和预测过程。

2.2 训练样本预筛选的分布式实现过程

如1.3 节所述,当采用KNN 算法对基于岭回归的协同预测模型进行改进时,需要在训练预测模型之前增加样本预筛选过程。传统方法需要收集汇总所有发电集团的样本数据,然后计算样本距离,完成样本筛选。这种集中式解决方案不仅难以满足数据隐私保护的要求,还需要占用大量的通信带宽和存储空间。为了解决上述挑战,本文提出了样本预筛选的一种分布式实现方法,具体流程如下。

步骤1:各发电集团首先利用本地数据集来构造kd 树。针对待预测时刻t,各发电集团首先获取各自在t时刻的输入特征向量xg,t∈Rng,然后根据待预测样本点的特征属性,利用kd 树进行快速KNN搜索,筛选得到距离最近的m个样本点,并将对应的样本索引集合Λg发送给中央协调者。

步骤2:中央协调者收集汇总来自各发电集团的样本索引集合Λg,然后求并集得到所有需要计算欧氏距离的样本索引集合Λ,即

随后,中央协调者将样本索引集合Λ返回给各发电集团。

步骤3:各发电集团接收来自中央协调者的样本索引集合Λ,然后计算待预测样本xg,t与训练集中各相应样本点xg,j(j∈Λ)之间的“局部”欧氏距离,组成向量dg∈R|Λ|,如式（9）所示。

式中:|Λ|表示集合Λ中所含元素的个数。

最后,各发电集团将自己计算出的“局部”欧氏距离向量dg∈R|Λ|发送给中央协调者。

步骤4:中央协调者收集汇总来自各发电集团的“局部”欧氏距离向量dg∈R||Λ,计算“全局”欧氏距离向量d∈R||Λ,如式（10）所示。然后,中央协调者挑选出“全局”欧氏距离最小的m个样本点,并将对应的样本索引返回给各发电集团。

步骤5:各发电集团接收来自中央协调者的样本索引信息,从各自的训练数据集中筛选出对应的m个历史样本点,构成各自的子训练集Xg∈Rm×ng以及yℓ∈Rm。

通过上述5 个步骤,实现了训练样本的分布式预筛选过程,相应过程如图1 所示。

图1 训练样本预筛选的分布式实现过程Fig.1 Distributed implementation process of training sample pre-screening

在该过程中,各发电集团可利用kd 树进行快速KNN 搜索,无须遍历整个训练数据集,可以显著提升计算效率。此外,各发电集团与中央协调者之间只需要交换距离向量dg∈R|Λ|和样本索引,无须传输各发电集团的历史数据集,故在满足数据隐私保护要求的同时,显著减少了通信传输和存储空间的需求。

2.3 岭回归模型的迭代求解算法框架

在完成了训练样本的预筛选后,可采用同步梯度下降（synchronous gradient descent,SGD）算法［21］来求解优化问题（式（7））,从而获得各发电集团的拟合参数向量θg(g=1,2,…,G)。采用SGD 算法求解岭回归模型的具体过程如下:

1）首先写出改进岭回归模型（式（7））所对应的目标函数J(θ):

式中:θ=[θT1,θT2,…,θTG]T为各发电集团参数向量构成的堆叠向量。

2）计算目标函数J(θ)关于拟合参数向量θk的梯度向量表达式,具体公式如下:

式中:k=1,2,…,G表示参与联邦学习过程的各发电集团。

3）利用梯度计算结果,对各拟合参数向量进行更新,具体公式如下:

式中:n∈N 为迭代次数；η为SGD 算法中参数更新的步长（也被称为学习率）。

4）计算拟合参数向量的相对变化Δθ(n)k∈R,具体公式如下:

根据Δθ(n)k的数值大小,可以判断能否终止训练迭代过程。

2.4 岭回归模型的分布式训练方法

步骤1:各发电集团收集原始数据,并在本地统一进行参数初始化,具体包括以下4 个部分。

1）对拟合参数向量θk进行随机初始化,使其服从正态分布,即θ(0)k～N(0,1)；

2）设置相同的正则化系数λ及学习率η；

3）设置相同的最大迭代次数,并将迭代计数器n归零,即设置n=0；

4）设置相同的拟合参数向量允许误差ε,并将Δθk的初值设置为正无穷大,即Δθ(0)k=+∞。

步骤2:各发电集团利用本地数据以及当前的拟合参数向量θ(n)k进行计算。其中,待预测对象ℓ 计算Xℓθ(n)ℓ-yℓ∈Rm,而提供辅助信息的相邻发电集团计算Xgθ(n)g∈Rm(g=1,2,…,G；g≠ℓ),然后各发电集团将计算结果发送给中央协调者。

步骤3:中央协调者收集汇总来自各发电集团的计算结果,并将这些计算结果进行加和,求和结果记为S(n)∈Rm,其具体表达式如式（15）所示。

接着,中央协调者将得到的求和结果S(n)∈Rm返回给各发电集团。

步骤4:各发电集团接收来自中央协调者的求和结果S(n),并结合本地数据以及相关参数值,继续进行本地计算,具体包括以下4 个部分。

1）利用式（16）计算本地梯度向量；

2）利用式（13）更新本地拟合参数向量θ(n)k；

3）利用式（14）计算Δθ(n)k；

4）迭代计数器加1,即设置n:=n+1。

步骤5:判断是否可以结束联邦学习的迭代过程,具体准则如下。

1）若对各发电集团而言,均有Δθ(n)k<ε,则可以提前终止联邦学习的迭代过程；

2）若迭代计数器n的数值达到了最大迭代次数,则终止联邦学习的迭代过程。

在步骤5 后,若迭代尚未终止则返回步骤2,继续迭代,直到满足迭代终止条件。改进岭回归模型的分布式训练过程如图2 所示。

图2 改进岭回归模型的分布式训练过程Fig.2 Distributed training process of improved ridge regression model

从图2 可以看出,与传统的集中式训练方法相比,本文提出的基于联邦学习机制的分布式训练方法具有以下3 个优点:

1）利用梯度向量可拆分计算的特点,将原始的大规模优化问题分解为大量的小规模子问题,且每个子问题都可在每个发电集团本地进行边缘计算。因此,不再需要大规模收集和处理数据,降低了通信负担和计算压力,提高了模型的训练效率；

2）各发电集团的隐私数据信息（包括风电功率历史数据、各类气象特征及模型拟合参数）只在本地计算时使用,并未发生传输或转移。在分布式训练结束后,各发电集团只能得到各自对应的拟合参数结果,无法获知其他参与者的隐私数据信息；

3）虽然各发电集团之间存在竞争关系,但在预测模型的分布式训练过程中,它们彼此无须交换任何数据。它们只与中央协调者交换SGD 算法迭代过程的中间计算结果,属于可共享的非隐私数据信息。因此,可以满足数据隐私保护的要求。

2.5 岭回归模型的分布式预测方法

在完成分布式训练后,各发电集团可以获得各自对应的拟合参数,接下来对待预测对象ℓ 的风电功率进行预测,相应的分布式预测过程如下。

步骤1:各发电集团基于待预测时刻t的输入特征向量xg,t∈Rng,结合分布式训练得到的拟合参数向量θg∈Rng,在本地进行计算,得到“局部”预测结果θTgxg,t∈R,并将其发送给中央协调者。

步骤2:中央协调者收集来自各发电集团的“局部”预测结果,并将所有“局部”结果加和,得到的求和结果即为待预测对象ℓ 在t时刻的风电功率预测值,其具体计算公式如式（17）所示。

最后,中央协调者将该预测结果ŷℓ,t∈R 返回给待预测对象ℓ 即可。上述分布式预测过程见图3。

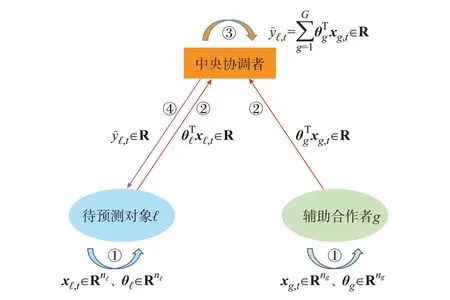
图3 改进岭回归模型的分布式预测过程Fig.3 Distributed forecasting process of improved ridge regression model

3 算例分析

3.1 数据集简介

2014 年全球新能源预测竞赛（GEFCom2014）提供了可用于风电预测的公开数据集［23］,它包含了10 个风电场站的历史数据,时间跨度自2012 年1 月1 日到2013 年12 月1 日,时间分辨率为1 h。各风电场站的历史数据组成如下:

1）4 个输入特征:距离地面10 m 处的纬度风速U10和经度风速V10,以及距离地面100 m 处的纬度风速U100和经度风速V100；

2）1 个输出特征:经过风电场站装机容量归一化后的风电功率测量值P；

10 个风电场站均位于澳大利亚,但由于数据安全和商业竞争的考虑,GEFCom2014 组委会没有对外披露它们的装机容量及经纬度信息［23］。

3.2 利用相关性分析寻找协同预测的合作伙伴

本文选择相关性分析法作为先验手段,筛选出了两组可参与联邦学习的最佳合作小组,详细过程见附录C。第1 组是1 号、7 号和8 号场站,记为A组；第2 组是4 号、5 号和6 号场站,记为B 组。

3.3 所提模型预测效果的评估结果

对于3.2 节确定的两组场站,以A 组场站为例（B 组与之相同）,假设其包含的3 个场站分属3 个不同的发电集团,且这些发电集团愿意通过参与联邦学习来提升预测精度。下面将以上述两组场站为例,对提出的协同预测模型进行算例分析。

在模型评估过程中,对于学习率η、正则化系数λ以及最邻近样本数m等超参数,均采用网格化搜索及10 折交叉验证法来确定其合适取值。

3.3.1 生成预测模型的输入特征

借助气象学知识,利用纬度风速U和经度风速V可以生成风速Ws和风向Wd。此外,根据风能利用的贝兹理论以及时间序列预测中的季节性特征,还可以生成其他输入特征。附录D 表D1 总结了所提风电预测模型的全部可用输入特征。

3.3.2 定义预测模型、预测方式及评估指标

为了方便模型的区分和比较,将1.2 节提出的岭回归模型命名为“标准岭回归模型”,将1.3 节提出的岭回归模型命名为“改进岭回归模型”。

为了合理评价预测模型的优缺点,定义以下两种预测方式:1）“独立预测方式”,仅使用待预测对象的相关特征信息,在待预测对象本地进行预测模型的训练和预测；2）“联邦预测方式”,待预测对象和辅助合作者相互协作,使用待预测对象和辅助合作者的相关特征信息进行预测模型的训练和预测。

本文将数据集按时间段划分为训练集和测试集,取2012-01-01 至2013-09-21 的数据作为训练集,用于模型训练；取2013-09-22 至2013-12-01 的数据作为测试集,用于模型性能评估。在进行超参数寻优或输入特征筛选时,本文采用了10 折交叉验证法,将训练集等分为10 个子集,对模型独立重复地进行10 次训练和验证。在每次训练时,取其中9 个子集对模型进行训练,留1 个子集作为验证集,对训练好的模型进行检验。

本节采用均方根误差（RMSE）以及平均绝对误差（MAE）作为预测模型性能的衡量标准,计算公式分别如式（18）和式（19）所示。预测模型在测试集上的RMSE 及MAE 越小,其预测精度越高。

3.3.3 联邦预测方式和独立预测方式的比较

在本节,使用标准岭回归模型,比较其在联邦预测方式和独立预测方式下的预测结果,以验证联邦预测方式在提升预测精度方面的优越性。

对于A 组（或B 组）,每次选取组内1 个风电场站作为待预测对象,其余风电场站作为辅助合作者,在两种不同的预测方式下分别进行测试,记录测试集上的RMSE 及MAE,结果如表1 所示。

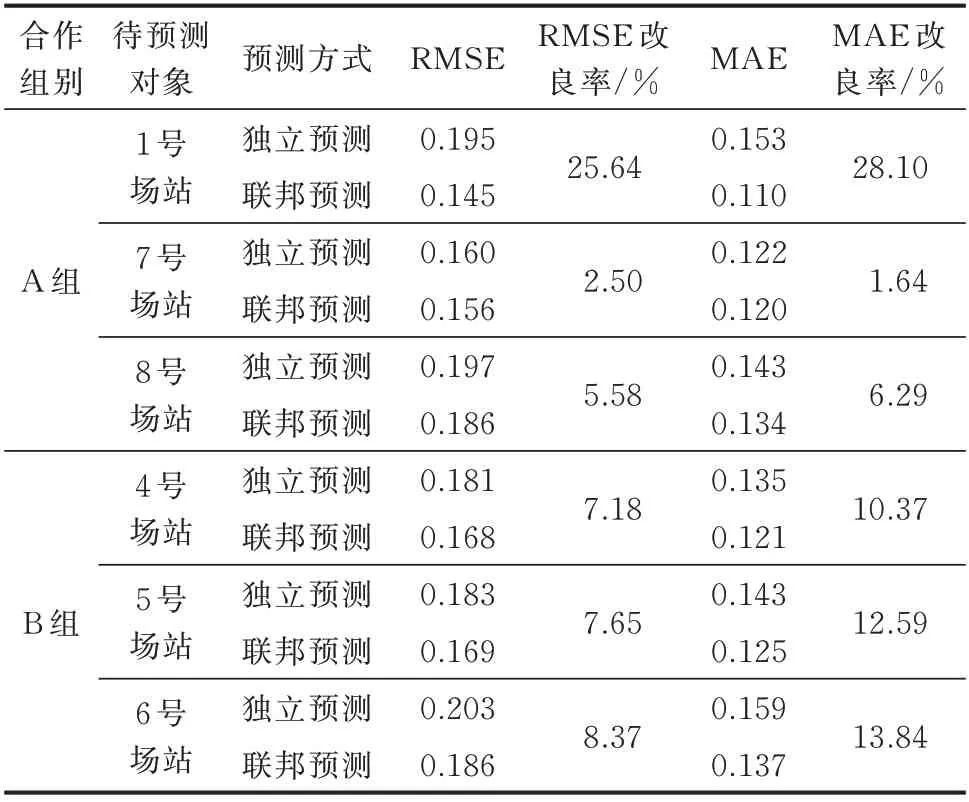
表1 标准岭回归模型在两种预测方式下的预测性能比较Table 1 Comparison of forecasting performance of standard ridge regression model with two forecasting methods

由表1 可以看出,各场站在独立预测方式下的预测误差RMSE 及MAE 均较大,而采用联邦预测方式后,各场站的预测误差都有了一定程度下降,预测精度都有所提升。其中,提升效果最显著的是1 号 场 站,其RMSE 改 良 率 达 到25.64%,MAE 改 良率达到28.10%。由此可见,相比于传统的独立预测方式,联邦预测方式充分利用了其他邻近场站的数据信息,弥补了单一场站数据特征不够全面的缺陷,较好地捕获了风电场站之间的时空相关性,从而减少了风电预测误差,增强了模型的泛化能力。

以1 号场站作为待预测对象,其在两种预测方式下的部分预测结果见附录D 图D1。从图D1 可以看出,采用联邦预测方式能够更好地捕获风电功率变化趋势,也能够明显缩小预测曲线与真实曲线之间的差距。因此,联邦学习预测模型比传统的独立预测模型在提升预测精度方面更具优势。

3.3.4 改进岭回归模型的预测效果

3.3.3 节验证了联邦预测方式比独立预测方式更有效,下面在联邦预测方式下,针对本文提出的基于改进岭回归的协同预测模型,验证1.3 节提出的两种改进措施的有效性。

表2 比较了使用KNN 算法改进前后,岭回归协同预测模型在测试集上的RMSE 及MAE。由表2可以看出,在联邦预测方式下,相比于标准岭回归模型,采用KNN 算法进行改进可以进一步减少预测误差,提高预测精度。其中,改善效果最显著的仍然是1 号风电场站,其RMSE 改良率达到了11.72%,MAE 改良率达到了16.36%。对于7 号场站,当采用KNN 算法进行改进时,其预测精度也有了较为明显的提升。由此可见,基于KNN 算法改进的岭回归模型能够有效改善预测模型的欠拟合现象,进一步提高风电功率预测精度。

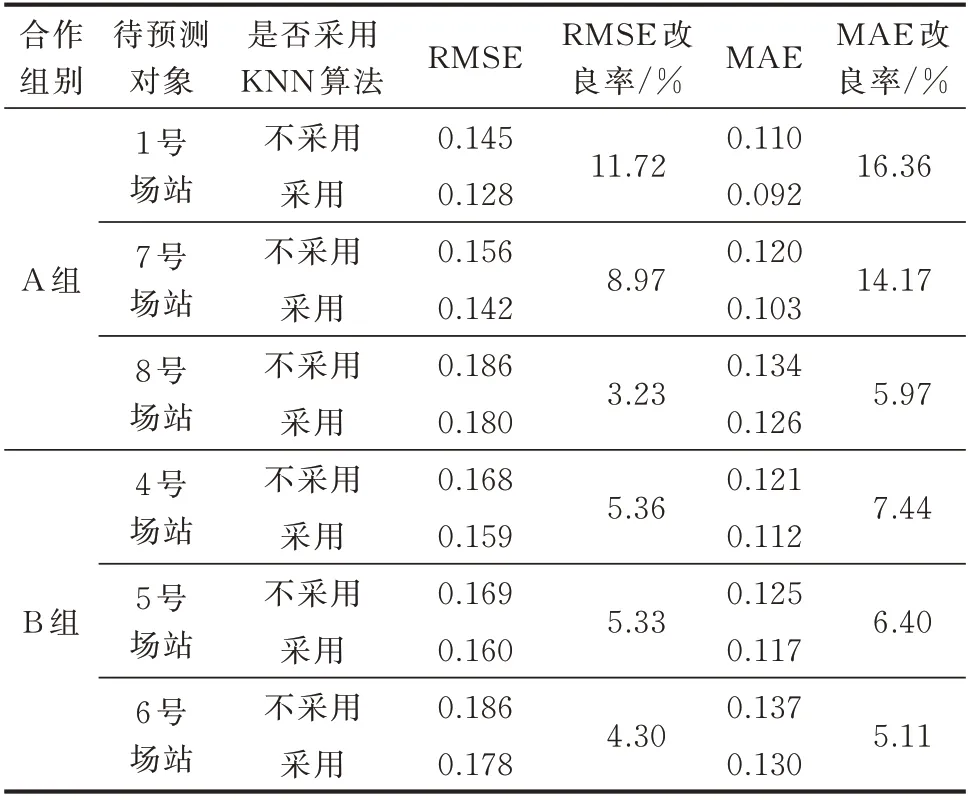
表2 岭回归模型在使用KNN 算法改进前后的性能比较Table 2 Comparison of performance of ridge regression model before and after using KNN algorithm

接下来,在使用KNN 算法进行改进的基础上,验证改进措施2（详见1.3 节）的有效性,结果见附录D 表D2。选取的深度学习方法包括MLP、GRU 以及LSTM 网络,所选模型中的超参数均经过网格化搜索及交叉验证法进行调优。从表D2 中可以看出,采用改进措施2 后,进一步减少了各风电场站的预测误差,提高了预测精度。其中,改善效果最显著的是6 号场站,其RMSE 改良率达到了6.74%,MAE改良率达到了9.23%。这表明,在使用KNN 算法进行改进的基础上,使用改进措施2 能够进一步提高预测精度。

图4 展示了以1 号场站为待预测对象时,改进岭回归模型和标准岭回归模型在相同时段的部分预测结果。从图4 可以看出,改进后的风电功率预测曲线更加贴近真实曲线,预测效果更好。

图4 1 号场站在岭回归模型改进前后的预测结果对比Fig.4 Comparison of forecasting results of wind farm 1 before and after improvement of ridge regression model

3.3.5 本文方法和深度学习方法的比较

3.3.4 节验证了1.3 节提出的两种改进措施的有效性,下面将本文提出的改进岭回归协同预测模型和已有深度学习方法的预测结果进行比较,以验证本文所提方法的优越性。采用的深度学习方法包括MLP、GRU 以及LSTM 网络,均使用单一场站的本地数据进行训练和预测,选出其中表现最好的模型进行展示,结果见附录D 表D3。从表D3 中可以看出,和单一场站使用已有深度学习方法的预测结果相比,本文提出的改进岭回归协同预测模型在提升预测精度方面具有一定的优势,其中改善效果最显著的是1 号场站,其余场站也均有一定幅度的提升。

3.3.6 协同预测模型的应用场景拓展

前面的算例分析部分均是以单个场站来代表单个发电集团,本节将对改进岭回归模型的应用场景进行拓展,考虑一个发电集团内含有多个场站的实际情况,进而说明本文方法的有效性和普适性。

观 察 附 录C 图C1 可 以 看 出,A 组 场 站（1 号、7 号、8 号）和C 组场站（3 号、9 号）之间的相关性较为明显,B 组场站（4 号、5 号、6 号）和D 组场站（2 号、10 号）之间的相关性较为明显。因此,考虑将上述4 组场站视为4 个发电集团,A 组可与C 组进行协作,B 组可与D 组进行协作。

表3 比较了各组场站之间协作或不协作时,各组场站的总风电功率预测结果。可以看出,采用本文提出的改进岭回归协同预测模型后,各组场站的预测精度均得到了明显的提高,验证了本文所提方法的有效性和普适性。

表3 各组场站在不同预测方式下的风电功率预测结果Table 3 Wind power forecasting results of each group of stations with different forecasting methods

3.4 改进岭回归模型的计算性能评估结果

3.4.1 模型计算精度的评估结果

为了使用其他邻近场站的数据信息,传统预测方法需要首先将各方数据汇聚到一起,然后再经过“集中式训练”得到最优预测模型,在本文中称为“集中式求解”。与之相对,本文提出的协同预测模型借助纵向联邦学习机制,采用了“分布式训练”框架,以此来解决不同数据拥有方在不交换机密数据的情况下进行协作的问题,在本文中称为“分布式求解”。附录D 表D4 比较了改进岭回归模型在集中式和分布式求解方法下的预测结果。从表D4 可以看出,改进岭回归模型在分布式方法下的预测结果与集中式方法完全一致,从而验证了分布式方法预测结果的可靠性与稳健性。

3.4.2 模型总耗时的评估结果

考虑从两个方面评估模型的总耗时,一是固定数据集大小,不断增加参与联邦学习的风电场站数目；二是固定风电场站数目,不断扩大数据集的规模。在上述条件下,让改进岭回归模型分别在集中式和分布式求解方法下完成一次训练和预测,统计相应的模型总耗时,结果如附录D 图D2 所示。从图D2 中可以看出,当所涉及的风电场站总数增多或数据集规模变庞大时,集中式求解方法的总耗时会显著增加,而分布式求解方法的总耗时却始终维持在较低水平。产生该现象的主要原因是分布式求解方法采用的是并行计算,故计算耗时通常比集中式方法要少。因此,在合作对象众多或数据量庞大的情况下,分布式求解方法通过并行计算可以获得较短的耗时,比集中式方法更具优势。

4 结语

针对短期风电功率预测问题,本文提出了一种基于联邦学习机制并使用改进KNN 算法的岭回归协同预测模型,设计了相应的分布式训练和预测方法。在联邦学习机制下,该协同预测模型以分布式方式间接利用了邻近其他风电场站的相关数据信息,在确保隐私数据安全的前提下,有效提高了风电功率预测精度,同时提升了预测模型的求解效率。本文通过实际算例验证了所提方法的有效性,由算例结果可以看出:

1）采用联邦学习机制,通过与邻近场站相互协作,以分布式方式间接利用邻近场站的数据信息,能够有效提高风电功率预测精度。

2）采用KNN 算法,根据待预测样本的属性来筛选训练样本,能够进一步减少预测误差,提高风电功率预测精度,增强模型的泛化能力。

3）在面对大规模的预测问题时,与传统的集中式求解方法相比,采用分布式求解方法能够保证计算结果的准确性,同时显著地减少计算耗时。

最后需要指出,本文所提出的预测模型一次只能针对一个待预测对象进行预测,目前还无法实现同时对多个待预测对象进行预测,这部分改进工作是未来研究的潜在方向之一。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。