时滞作用下HIPK1-PAGE4-CLK2网络的Hopf 分岔
黄 榕,陈亦佳,郭丽丽,周颖鸿,张 远
(玉溪师范学院 数学与信息技术学院,云南 玉溪 653100)
固有无序蛋白(IDPs)独特的结构和存在形式在许多细胞功能中扮演着重要的角色,成为现代结构生物学和蛋白质组学研究的重要组成部分[1].IDPs 在真核生物中大量存在[1-4],是一种天然丰富的功能性蛋白质[5],在其自身条件下没有稳定的三维结构[1-6-7-8],因而被称为是固有无序蛋白[1-6].这些蛋白以具有高度可塑性的构象群而存在[1-6-7-9-10-11],调节了许多生物学过程,例如转录、翻译、信号传递[2],细胞信号调控,分子识别,信号转导,细胞周期[2-3-12],昼夜节律[13],大分子阵列的组装[4],核糖体等大分子机器的有序组装等[2-14].由于固有无序蛋白调节许多重要的生命过程[5],因此其突变或细胞丰度的变化常常会导致多种疾病的产生,癌症就是其中的一种[2-15].
前列腺相关基因4 是一种在结构和功能上都具有相对较好特征的IDP[16-17-18],即使在与其生物学靶标相互作用时仍保持很大程度的无序性,并且在人类男性中具有显著的前列腺特异性[16-17-19].PAGE4 具有原癌基因的特征存在于胎儿前列腺中的发育过程中[16-20],在多能干细胞中高度表达[20].此外,PAGE4蛋白的表达在PCa 中因其响应于多种应激因子而被上调[17-20-21].PAGE4 在S9 和T51 被(HIPK1)磷酸化[16-20],并结合增强肿瘤蛋白C-Jun[10-18-20-22-23].HIPK1 是细胞应激反应途径的一个组成部分[20].C-Jun也是应激反应途径的组成部分,并与Fos 家族的成员异二聚体化,以形成激活蛋白-1(AP-1),在前列腺的发育和病理过程中扮演着重要的角色[10-18-20].另外,CLK2 是一种双特异性激酶,其磷酸化剪接体复合物中富含丝氨酸(SR)的蛋白质,也能磷酸化PAGE4[24-25].但结果显示与HIPK1 相反,CLK2 在多个S/T 残基处磷酸化PAGE4,包括S9 和T51[26].实验研究证明,HIPK1 和CLK2 在雄激素依赖性或非依赖性的PCa 细胞中表达,并且两种激酶在PCa 中上调.HIPK1 和CLK2 对PAGE4 的磷酸化在C-Jun 反式激活方面具有相反的功能[18].因此,响应于HIPK1 和CLK2 的差异磷酸化,磷酸化PAGE4 具有不同的构象偏好[10].总体而言,磷酸化诱导的PAGE4 构象动力学可能在调节PCa 的表型可塑性中发挥作用.
众所周知,时滞是自然界普遍存在的一种现象[27].在动力系统中,时滞的存在使得系统随时间的演化不仅取决于当前的状态,也取决于过去的状态[28-31].时滞涉及多种生物网络,例如基因调控网络[32-33],神经网络系统,病毒免疫模型[34]等.研究具有实际应用背景的时滞微分方程的动力学行为(如平衡点的稳定、分岔以及混沌等)已经成为一个热门的研究课题.为了研究PAGE4 构象的振荡动力学在PCa中的作用,Prakash 等人构建了一个时滞HIPK-PAGE4-CLK2 网络微分方程模型[20],然而,研究者主要采用数值仿真的方法,理论上对于该模型的理解仍然不清楚.特别地,需要阐明支持稳定周期振荡解存在的充分条件,且当满足这些条件时所需的最小时滞.此外,时滞的临界值如何依赖于其他物理参数仍需阐明.
基于上述考虑,本文将系统地讨论时滞对HIPK-PAGE4-CLK2 网络动力学的影响.首先将时滞τ作为分岔参数,推导出系统稳定的条件.其次,运用Hopf 分岔理论,分析Hopf 分岔的存在性.最后,利用数学软件Mathematica 10.0 进行数值模拟,验证理论分析的正确性.
1 模型介绍
由Prakash[20]等人提出的时滞HIPK-PAGE4-CLK2 网络模型如下:
其中
2 正平衡点稳定性和Hopf 分岔存在性
其中
可以得到线性化方程(3)的特征方程
由(4)可以推导出
其中
接下来,通过两种情况讨论(5)的根的分布情况.
情况一:τ=0 ,此时(5)可以化简为
由Routh-Hurwitz 准则,当下列不等式成立时
情况二:τ>0 时.设(5)有纯虚根,则
进一步得
通过计算,得到以下等式
即
其中
令
此外,容易验证
将0ω带入(8),我们将得到时滞的临界值:
其中j=0,1,2,….
把λ(τ)带入(5)并对τ求导得到
化简得
因为
所以
因此,第二横截条件成立.
定理(i)如果成立,则当τ=0 时,系统(1)在正平衡点是局部渐近稳定的.(ii)如果且δ2-γ2< 0都成立,则当时滞时,系统(1)在正平衡点是局部渐近稳定的,当τ>τ0时不稳定. 此外,当τ=τ0系统在平衡点产生Hopf 分岔.
3 数值模拟
在本节中,为了验证上述获得的理论结果,使用Mathematica10.0 软件进行数值模拟.用以下参数数据进行数值模拟:模型(1)转化成以下等式
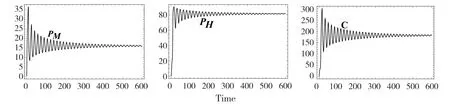
图1 当τ = 6 < τ0 时,系统(1)的数值模拟.
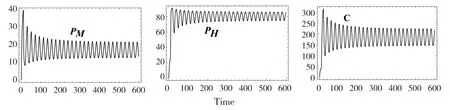
图2 当τ = 8 > τ0 时,系统(1)的数值模拟.
4 结果与展望
本文在前人工作的基础上,运用微分方程分支理论和利用数学软件Mathematica 研究了时滞对HIPK1-PAGE4-CLK2 网络动力学的影响,通过对线性化特征方程的讨论,得到判定模型在正平衡点处的稳定性和Hopf 分岔存在的充分条件;数值模拟很好地验证了理论分析结果的正确性.研究结果表明,时滞在调控HIPK1-PAGE4-CLK2 网络的动力学中起着至关重要的作用,它能够通过发生Hopf 分岔使网络的稳定性发生切换,产生持续的周期振荡.

