BL Lacs 天体1823+568 射电波段光变周期分析

石苒力，普燕梅，赵德英，李怀珍

（玉溪师范学院 物理与电子工程学院，云南 玉溪 653100）

光变是耀变体一个非常重要的特性，能反映出耀变体很多物理性质．耀变体的光变现象，尤其是周期性光变现象，可以帮助我们很好地理解耀变体的辐射机制[1-2]．例如周期性光变能帮助我们有效地确定耀变体的物理参数，并有效地限制它们的辐射模型[1]．根据光变时标的长短，耀变体的光变分为一天量级光变，短时标光变和长时标光变．短时标的时标一般从几周到几个月，而长时标光的时标一般以年为量级[3-5]．

1823+568 是一个蝎虎座BL 型天体（BL Lacs），其红移为z=0.664 ±0.001[6]．观测发现BL Lacs 天体1823+568 寄主星系为椭圆星系并存在kpc 尺度的复杂喷流形态[7-8]．观测还发现该天体存在强极化、超光速、高且变化的偏振现象[9-10]．甚大天线阵观测发现BL Lacs 天体1823+568 存在喷流摆动现象，该现象可能是由螺旋磁场结构或者喷流的进动引起的[8]．Schramm 等人在1994 年首次研究了BL Lacs 天体1823+568 的光变并确认了一些大于0.5 个星等的快速光变现象[11]．2012 年，刘祥等人利用甚大基线干涉仪在15GHz 的观测数据，发现该天体存在大约7 年的周期性光变时标，并且他们用弹道喷流加进动模型解释了周期性光变现象[12]．李怀珍等人分析BL Lacs 天体1823+568 在光学波段的光变数据，发现其光学波段存在283 天的光变周期，并利用双黑洞系统轨道运动驱动的非弹道喷流运动模型解释了该周期性光变现象[13]．此外，Lister 等人利用MOJAVE 项目的观测数据发现BL Lacs 天体1823+568 的喷流存在非弹道运动[14]，Roland 等人报道了该天体中心存在双黑洞系统[6]．

1 观测数据和光变曲线

基于欧文斯谷射电天文台（OVRO）40 米射电望远镜的数据库，本文收集了BL Lacs 天体1823+568在射电15GHz 的光变数据[15]．欧文斯谷射电天文台40 米望远镜为了支持Fermi 伽玛射线空间望远镜的观测，于2008 年开始观测Fermi 伽马射线空间望远镜观测的耀变体目标，这有利于我们更好的理解耀变体的辐射性质．本文收集的光变观测数据的观测时间跨度是从2008年1月9日到2014年5月16日，约6.4年的时间．光变曲线见图1.

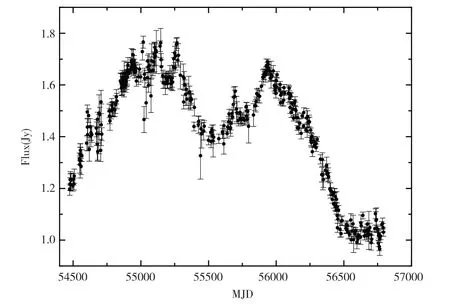
图1 BL Lacs 天体1823+568 在射电15GHz 的光变曲线

从图1 可以看出，BL Lacs 天体1823+568 在射电15GHz 的辐射存在剧烈变化，辐射流量最大值和最小值分别是Fmax＝1.766Jy和Fmin＝0.966Jy，流量变化为ΔF=0.8Jy．对于耀变体辐射变化，光变指数是一个很好的参数来描述光变行为，其定义如下[16-17]：

光变指数的不确定度由下列公式给出[18-19]：

其中σmax和σmin分别为最大流量和最小流量对应的误差．当光变指数和其不确定度之间满足V≥ 3ΔV时，光变被认为是显著的[20]．基于公式（1）和（2），BL Lacs 天体1823+568 在射电15 GHz 的光变指数为V=0.29 ±0.013．这表明该天体在射电15GHz 波段的光变是显著的.

2 光变时标分析

2.1 Lomb-Sclargle 周期图法分析光变时标

Lomb-Sclargle 周期图（LSP）是一种被广泛应用于时间序列分析的传统的分析方法，该方法由Lomb在1976 年提出[21]，Scargle 在1982 年对其进一步完善[22]．Lomb-Sclargle 周期图能很好地分析时间序列中存在的时标，对于一个时间序列，周期图可由下面的公式给出

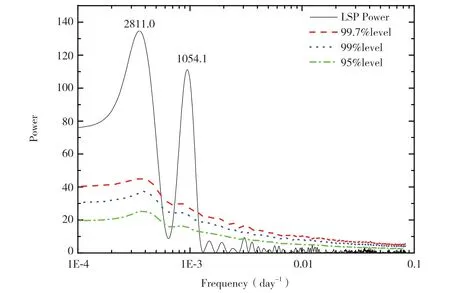
图2 Lomb-Sclargle 周期图方法的分析结果

2.2 Jurkevich 方法分析光变时标

为了检验Lomb-Sclargle 周期图方法所得结果的可信性，本文将采用Jurkevich 方法[25]对BL Lacs 天体1 823+568 的射电15GHz 光变曲线进行时标分析．Jurkevich 方法是Jurkevich 在1971 年为了分析不均匀的天文观测数据提出的一种时序分析方法，该方法是基于均方差期望值的一种统计方法，使用相位折叠技术来检验一系列测试周期．根据相位，观测数据被分成m组，每组的偏差和总的偏差由下列方程给出：

其中xi和ml分别是单个观测数据和第l组的观测数据点数．如果光变数据中存在周期性，那么当测试周期等于真正的周期时，总的偏差将达到最小值．为了检验所得结果的可信度，Kidger 等人在1992 年提出了f检验[26]，参数f由下式给出：

当f≥ 0.5 时，表示所得结果的显著水平是非常高的．如果f＜0.25，则表示所得周期是非常弱的，甚至是一个虚假的周期．图3 给出了Jurkevich 方法计算BL Lacs 天体1 823+568 的射电15 GHz 光变曲线的结果，结果显示在时标1 031 天处出现极小值，对应的总的偏差为=0.41，参数f=1.44 ＞ 0.5 这表明该周期是非常显著的．此外，该结果与Lomb-Sclargle 周期图方法所得结果是完全一致的.

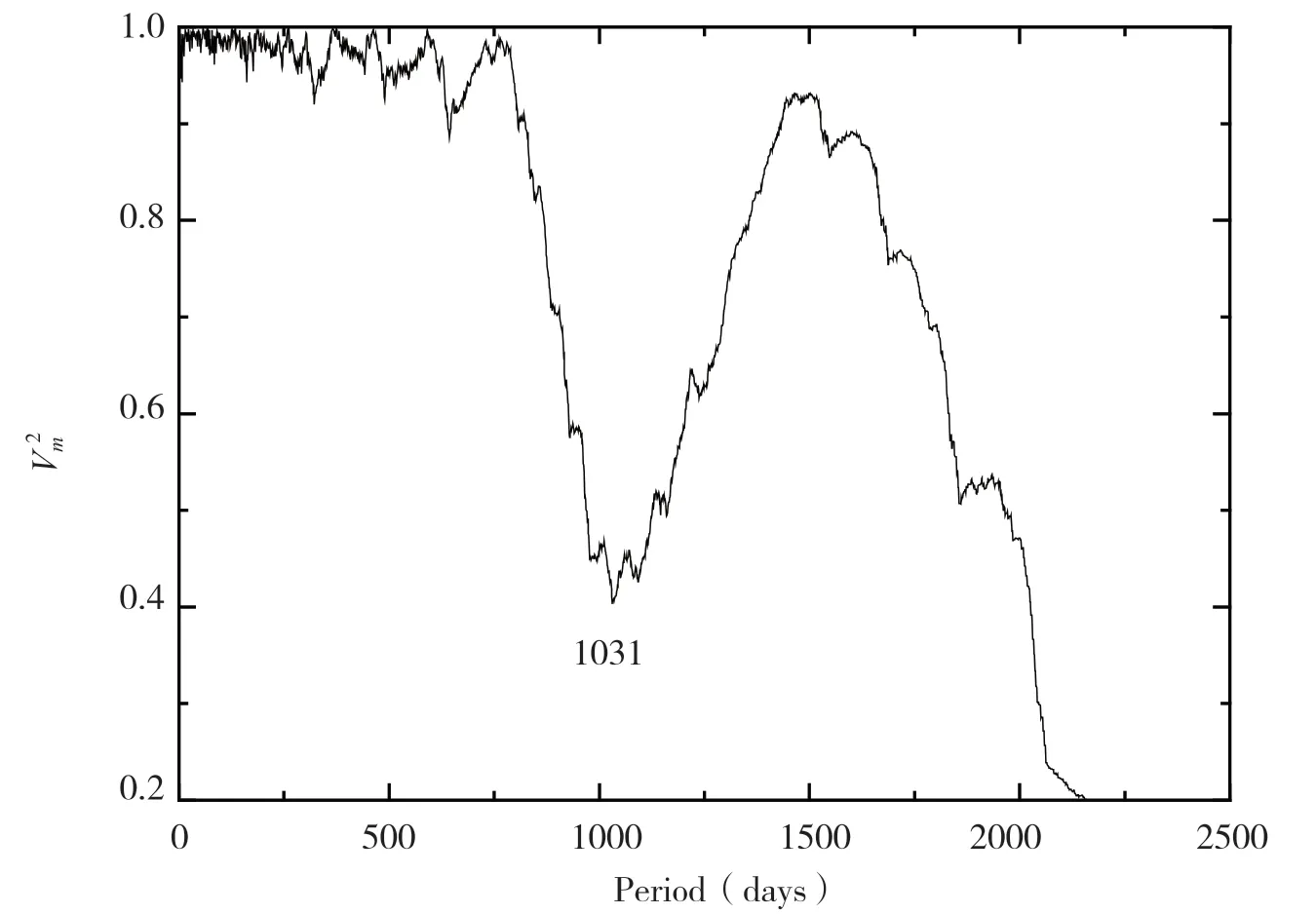
图3 Jurkevch 方法的分析结果

2.3 DCF 方法及分析结果

为了进一步检验Lomb-Sclargle 周期图方法所得结果的可信性，本文还采用离散相关函数（DCF）方法对BL Lacs 天体1 823+568 射电15GHz 的光变观测数据进行分析．Edelson 和Krolik 在1988 年的文章对DCF 方法的算法进行了详细的描述[27]．DCF 方法可以用来分析两个时间序列之间的相关性，同时也可以分析一个时间序列中的变化时标．如果时间序列中存在周期T，那么在DCF 曲线中将在τ=0 和τ=T出现极大值．DCF 方法的分析结果由图4 给出．从图4 可以看出，DCF 曲线中在τ=999天处出现极大值，这表明光变曲线中可能存在999 天的周期，这与Lomb-Sclargle 周期图方法和Jurkevich 方法得到的结果是一致的.

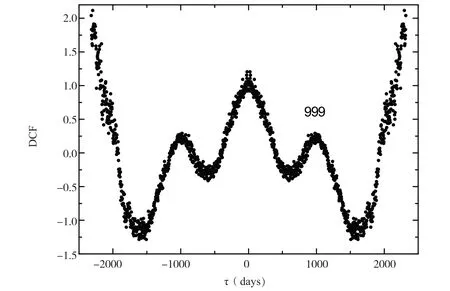
图4 DCF 方法的分析结果

3 结论和讨论

本文收集了BL Lacs 天体1 823+568 射电15GHz 的光变观测数据，利用Lomb-Sclargle 周期图方法、Jurkevich 方法和DCF 方法对其光变数据进行时标分析，分析结果显示BL Lacs 天体1 823+568 射电15GHz 的光变曲线中存在P=1 054.1 ±185.1天的光变周期，该周期约是李怀珍等人分析光学R 波段所得283 天周期的4 倍[13]，他们之间可能存在天文学倍频关系．BL Lacs 天体1 823+568 在射电15GHz 的光变曲线中存在的P=1 054.1 ±185.1天的周期能在几何模型下得到很好的解释[28-31]．在光变周期的几何图景下，周期性光变可能是由多谱勒聚束因子的周期性变化引起的，而多谱勒聚束因子的变化一般是与视角的变化有关．对于多谱勒聚束因子周期性变化的驱动机制，Rieger 在2004 年提出了3 种驱动机制，它们是喷流的内禀旋转，双黑洞轨道运动驱动和喷流进动驱动，它们对应的观测周期分别为≤10 天、≥10天和≥1 年[28]．所以，本文所得结果可能是由于BL Lacs 天体1 823+568 中心存在进动喷流，进而引起多谱勒聚束因子的周期性变化引起的.