Blazar天体3C 66A光学波段准周期光变分析

程 岩 刘 风 孙中诺 董富通

(1 德州机电工程学校信息工程系 德州 251200)

(2 德州科技职业学院信息工程系 德州 251200)

1 引言

Blazar是活动星系核(AGN)的一个子类, 它是一种活动非常剧烈的天体. 光变是Blazar天体的一个重要特征, Blazar天体在全波段都会表现出剧烈的光变, 光变时标从几分钟到几十年不等[1–2]. 寻找和研究这类天体的光变特性对于认识它们的内部结构有重要的意义. 比如根据Blazar天体的天内光变(光变时标小于1 d), 可以推测其辐射区的尺度以及中心黑洞的质量等[3–4].

大量研究发现, Blazar天体的光变在多个波段存在周期/准周期的变化. 在光学波段, Fan等[5]整理了10个射电选BL Lac天体的光变数据, 并在其中9个天体中找到了周期为1.4–17.85 yr的周期光变; Graham等[6]研究了PG 1302–102的光学光变数据, 并发现了(1884±88) d的光变周期; Rani等[7]在Blazar天体S5 0716+714的光学R波段发现了时标为～15 min的准周期光变. 在X射线/γ射线波段人们也发现了大量的准周期光变的证据. 比如:Espaillat等[8]在3C 273的X射线光变数据中发现了时标为～55 min的准周期光变; Rani等[9]分别在AO 0235+164和1ES 2321+419的X射线数据中发现了时标为17 d和420 d的光变周期; Ackermann等[10]在PG 1553+113的γ射线波段发现了2.2 yr的光变周期; Zhou等[11]在PKS 2247–131的γ射线光变数据中找到了～34.5 d的准周期光变. 而在射电波段也有大量的Blazar天体被发现具有准周期光变行为, 比如: AO 0235+164[12–13]、PKS 1510–089[14]、NRAO 530[15]和PKS 1156+295[16]等; 另外, Ciaramella等[17]和Fan等[18]分别研究了两个样本的Blazar天体多个波段的射电数据并发现了周期性光变.

Blazar天体3C 66A从射电波段到γ射线波段都表现出明显的光变. 在X射线波段, Ghosh等[19]发现了时标为几小时的天内光变. 这种光变也存在于红外波段和射电波段[20].γ射线波段存在时标为1.5 d的光变[21]. 在光学波段, 人们发现了很多周期性光变的证据. Lainela等[22]发现了65 d的光变周期, 但是这一周期在后续的观测和研究中并没有得到证实. 而最新的观测数据表明存在其他的光变周期, 比如: Fan等[23]使用13 yr的光学V波段观测数据找到了～156.0 d和～1.96 yr的光变周期. Belokon等[24]和Kaur等[25]分别分析了3C 66A不同时间段的光变数据, 都发现了时标为2.5 yr的准周期光变.Otero-Santos等[26]分析了3C 66A光学R波段和V波段的数据, 找到了时标为3 yr的光变周期. 为了进一步确定3C 66A的光变周期,更好地认识其内部物理性质, 本文收集了2003—2021年间约18 yr的光学观测数据, 并使用了不同的方法对其进行了分析.

2 观测数据

3C 66A在光学波段有很长时间的观测历史, 我们收集了光学V波段的星等数据进行光变分析. 本文数据主要有3个来源, 第1个是Fan等[23]使 用 上 海 天 文 台(ShAO)1.5 m望 远镜观测的数据(时间范围2003—2009年), 第2个是通过AAVSO (The American Association of Variable Star Observers)数据库获得(2003—2021年)1https://www.AAVSO.org的数据, 最后一个是来自于Steward天文台的观测数据(2009—2018年)[27]. 图1给出了3种数据综合之后的光变曲线, 其中横坐标为儒略日(Julian Date, J.D.). 图中共2304个数据点,总的时间跨度约为18 yr, 平均时间间隔为2.7 d, 最大时间间隔为237 d. 之前的研究发现3C 66A的典型的光变周期在1.96–3 yr之间, 所以这些数据的时间间隔对于我们寻找年量级的光变周期不会有很大影响.

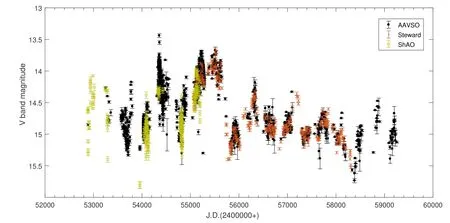
图1 3C 66A光学V波段的历史光变曲线, 图中不同来源的数据使用了不同的符号及颜色来表示.Fig.1 The historical light curve of 3C 66A in the optical V band. Different colours and symbols denote data from different observations.

3 光变周期分析

3.1 Jurkevich方法

为了研究3C 66A的准周期光变行为, 我们首先使用了Jurkevich方法对其光变曲线进行了分析来寻找光变周期. Jurkevich方法属于“相位折叠方法”, 非常适用于处理非等间隔数据, 并已经被广泛用于Blazar天体的周期分析中[28–29]. Jurkevich方法的原理是根据不同的测试周期, 按照相位不同将数据划分到m个分组中, 计算每一组的离均差平方和, 进而得到所有组的总离均差平方和V2m[30].V2m的极小值对应的试验周期就接近样本的真实周期. 但是V2m的值还会受到很多因素的影响, 比如分组数、数据样本本身的采样方式等,会导致V2m出现很多虚假极小值. 因此, Kidger等[31]提出了周期真实性的F判据:

一般情况下, 如果F≥0.5, 表明数据中有较强的周期, 而如果F≤0.25, 表明数据的周期比较弱.

图2给出了我们对3C 66A光学V波段星等数据的Jurkevich分析结果. 图中有两个比较明显的极小值, 其中第1个极小值为V2m= 0.776, 对应的F=0.29. 第2个极小值为V2m= 0.72, 对应的F= 0.39.根据F判据,F值的两个极小值都大于0.25, 说明它们所对应的周期很可能是数据的真实周期. 这两个周期值分别为(850±90)d和(1150±140)d, 其中周期误差是由V2m曲线中这两个极小值对应的半峰全宽所得到的. 我们所得到的(850±90)d周期与Fan等[23]在V波段发现的(1.96±0.63)yr周期在误差范围内是一致的, 但是我们的结果中并没有出现他们所发现的～156.0 d光变周期. Otero-Santos等[26]分析了光学R波段的数据得到了2.28 yr和3.14 yr的光变周期, 而我们的结果与此非常一致.

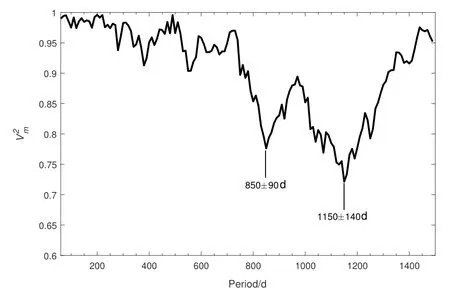
图2 3C 66A光学V波段数据的Jurkevich方法分析结果Fig.2 The Jurkevich test result for the period search in the optical V band of blazar 3C 66A

3.2 Lomb-Scargle方法

Lomb-Scargle (LS)方法是分析天体准周期光变的一种非常有效的方法, 它使用正弦波来模拟光变信号, 并利用最小二乘法对光变数据进行拟合,因此该方法非常适用于处理非等间隔数据[32–33].图3给出了我们用LS方法计算的3C 66A光学V波段的能谱, 其中有两个明显的峰值, 对应的周期值分别为(869±70)d和(1111±90)d. 其中的误差是由LS能谱减去蒙特卡罗模拟的平均能谱后峰值的半峰全宽(FWHM)获得(关于这一过程, 我们在下面会做详细说明). 这一结果与我们用Jurkevich方法所得的结果是相同的, 另外在LS能谱中也没有发现明显的～156 d光变周期.

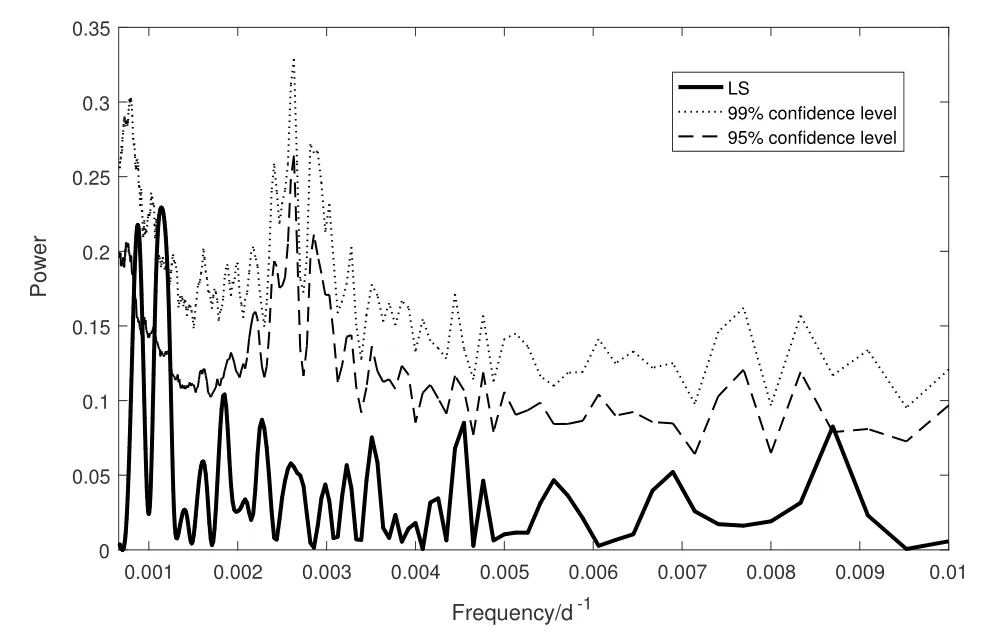
图3 3C 66A光学V波段数据的LS能谱, 图中还给出了1000次蒙特卡罗模拟得到的95%和99%的置信水平.Fig.3 The LS power spectra of the optical V band of 3C 66A, along with that of the 95% and 99% confidence level generated by 1000 Monte Carlo simulations.

Blazar天体的光变数据中通常包含一种随机过程, 该过程的傅立叶变换能谱一般表现出幂律谱的形式:p(f)∝f-α(α≥1), 其中p(f)表示随机过程的傅立叶变换能谱,f表示频率. 这种随机过程称为“红噪声”. “红噪声”对Blazar天体的光变会产生重要的影响, 主要表现为在较长的光变时标下会产生较大振幅的随机光变[34]. 这种随机光变通过一般的周期分析方法很容易被误认为周期信号. 因此为了评估所得周期的真实性, 我们需要在计算中考虑这种“红噪声”过程.

我们使用了能谱响应方法(PSRESP)[35]来评估“红噪声”对3C 66A光变数据的影响. 该方法已经被广泛用于活动星系核的能谱分析中了(比如:Chatterjee等[36]、Bhatta等[37]). 它使用一个简单的幂律谱来模拟“红噪声”的傅立叶变换能谱, 通过蒙特卡罗方法模拟出光变曲线, 与真实的光变曲线进行统计量比较, 得到“红噪声”的能谱, 进而可以评估“红噪声”对光变数据的影响.

本文使用幂律谱p(f)∝f-α来模拟3C 66A光变曲线中的“红噪声”,α的取值范围为1–2.5共20个点. 首先将光变曲线进行傅立叶变换, 得到真实的傅立叶变换能谱.之后使用Timmer等[38]的方法,将不同α值的幂律谱进行1000次的蒙特卡罗模拟, 并计算它们能谱的平均值. 通过比较真实能谱与这些平均能谱, 得到了斜率α的连续分布函数(如图4所示), 其中最大值对应的就是最佳拟合的α值. 我们得到的最佳拟合斜率α= 1.56±0.25, 其误差是由图4中斜率α的连续分布函数的半峰全宽得到的. 由此我们得到了最佳拟合能谱模型如图5所示.

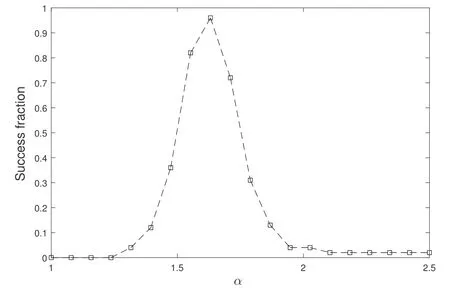
图4 3C 66A能谱斜率α的连续分布函数Fig.4 The success function of the power spectra slopes α of 3C 66A

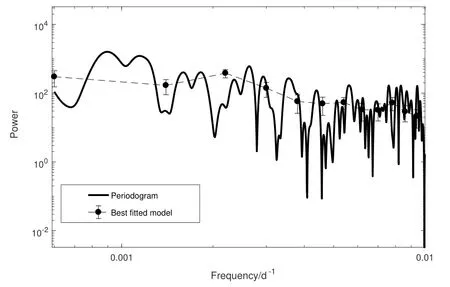
图5 3C 66A光学V波段数据的能量谱及其最佳拟合模型Fig.5 The power spectra of 3C 66A in the V band, along with the best fitted model

最后我们使用上面得到的最佳拟合模型对光变曲线进行了1000次模拟, 对每一次模拟的光变曲线进行重新采样, 使其与真实的光变曲线的采样率相同. 使用这些模拟的光变数据, 我们建立了关于图3中LS能谱峰值的置信水平. 其中(869±70)d的周期对应的峰值具有＞99%的置信水平, 而周期值为(1111±90)d的峰值置信水平为＞95%, 而图中其他峰值的置信水平都低于95%, 说明并没有其他在统计上比较显著的周期存在.

4 讨论

我们收集了来自于ShAO、AAVSO和Steward天文台3个来源的Blazar天体3C 66A的光学V波段18 yr的光变数据, 并使用Jurkevich方法和Lomb-Scargle方法两种方法研究了其准周期光变行为, 找到了～850 d (2.3 yr)和1150 d (3.2 yr)的光变周期.这一结果证实了之前对3C 66A准周期光变的研究.Belokon等[24]研究了3C 66A在1972—1992年间光学B波段的光变数据, 并发现了～2.5 yr的光变周期; Kaur等[25]分析了2005—2016年间的R波段数据同样找到了～2.5 yr的光变周期;而我们使用2003—2021年间的V波段数据得到了～2.3 yr的光变周期,另外Otero-Santos等[26]使用了2005—2020年间R波段的光变数据同样得到了～2.3 yr的光变周期, 这些结果足以说明～2.3 yr的光变周期在3C 66A的历史光变数据中是持续存在的. 而对于3.2 yr的光变周期, 在较早的观测以及研究中并没有发现该周期, 而且Otero-Santos等[26]研究发现该周期只存在于3C 66A的高活跃状态(辐射流量较高的状态), 说明该周期并非稳定周期.

为了验证这一结论, 我们分别使用周期为2.3 yr和3.2 yr的正弦函数拟合了3C 66A的光学V波段光变曲线, 其结果如图6所示. 为了更清楚地表示其长周期光变趋势, 我们将光变曲线做了50 d的平滑处理. 首先在图中可以看出3C 66A的长周期光变并不是严格的正弦形式, 而且在整个时间范围内经历了高活跃状态(J.D. 2456000之前, 平均星等值为14.38)和低活跃状态(J.D. 2456000之后, 平均星等值为14.9)两种状态. 因此我们使用单一的正弦函数并不能很好地拟合其光变曲线, 但是通过比较光变曲线和正弦函数的变化趋势, 我们可以判定前面所获得周期的可靠程度. 其中周期为3.2 yr的正弦函数在J.D. 2456290之前与光变曲线的变化趋势基本相同, 而在J.D. 2456290之后其与光变曲线出现了比较大的偏差. 这验证了我们之前的结论,即3.2 yr的周期并不是稳定周期, 并且只出现于3C 66A 的高活跃状态. 而周期为2.3 yr的正弦函数虽然其振幅与真实数据相差较大, 但是其总体变化趋势与光变曲线是比较一致的. 这同样也验证了我们之前的结论, 即2.3 yr的光变周期是一个稳定周期. 虽然3.2 yr的光变周期并不稳定, 但是它对3C 66A的长周期光变有着重要影响. 实际上, 如果我们使用3.2 yr和2.3 yr两个周期同时拟合3C 66A的光学V波段光变曲线, 可以得到较好的拟合效果.其结果如图6所示, 虽然在某些部分拟合曲线与光变曲线有较大的偏差(可能受到微光变或其他光变机制的影响), 但是总体上拟合曲线与光变曲线的变化趋势基本一致.

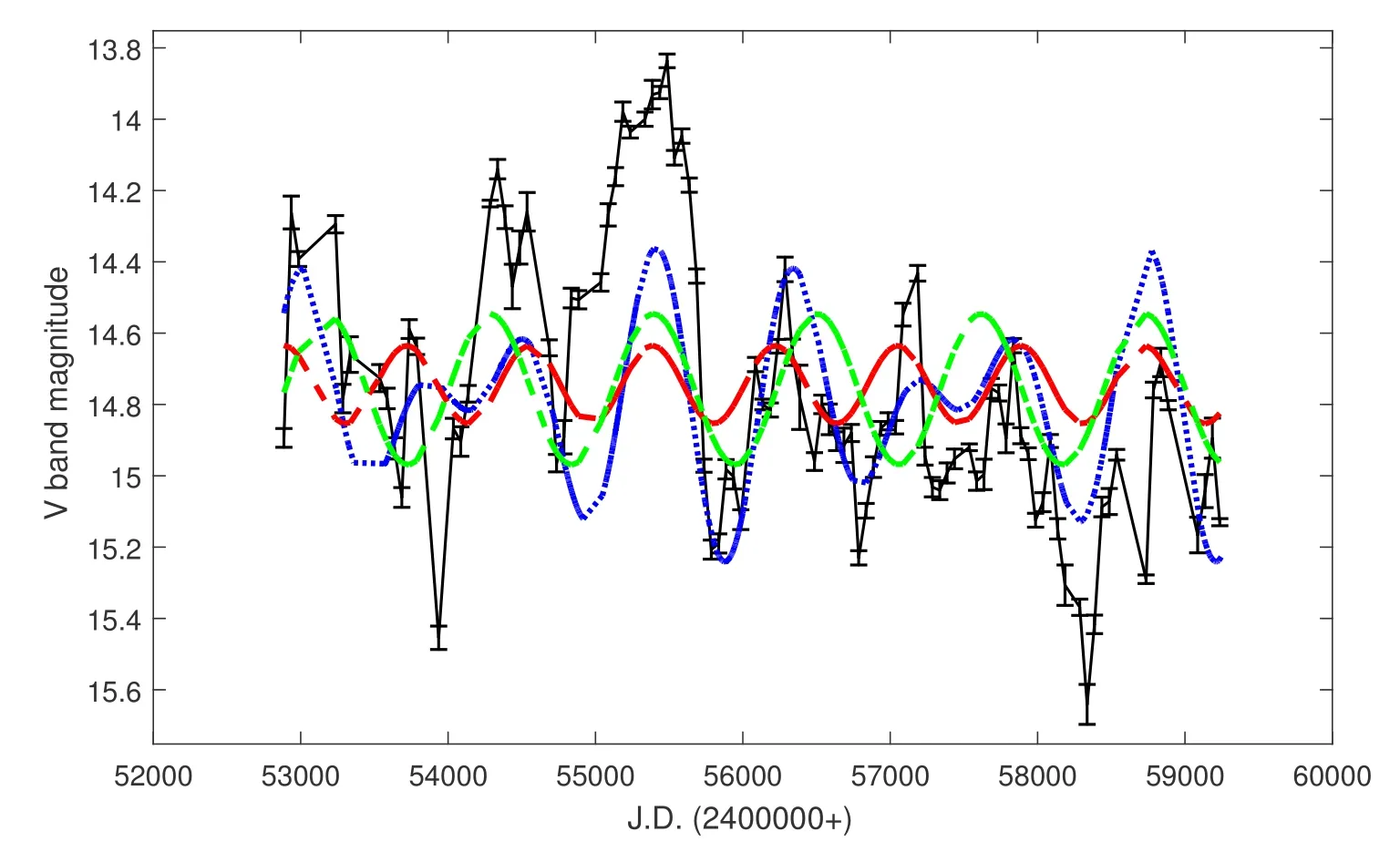
图6 3C 66A光学V波段历史光变曲线的正弦拟合结果, 黑线表示3C 66A光学V波段的光变曲线, 红色和绿色的虚线分别表示周期为2.3 yr和3.2 yr的正弦曲线, 而蓝色虚线表示这两个周期的拟合结果.Fig.6 Sinusoidal fit to the historical light curve of 3C 66A in optical V band. The black line represents the light curve, the red and green dashed lines are sinusoidal functions with periods 2.3 yr and 3.2 yr respectively, and the blue dashed line is the result of fitting with the two periodicities.

人们提出了各种模型来解释Blazar天体的周期性光变, 其中比较成功的模型是超大质量双黑洞模型. Sillanp¨a¨a等[39]提出了该模型, 并解释了OJ 287光学波段～12 yr的周期光变. 双黑洞轨道运动可能导致周期性的吸积, 吸积盘的进动以及喷流的进动和喷流的扭曲, 进而产生周期性光变[40–42]. 如果3C 66A的2.3 yr光变周期是由双黑洞轨道运动造成的, 那么我们可以根据开普勒运动公式估计其轨道半径为:

其中Tobs为观测周期,G为万有引力常数.3C 66A的中心黑洞质量近似为M ～8.57×108M⊙[25], 其红移值为z= 0.444[43]. 根据不同的观测, 其多普勒因子δ有不同的取值, 其变化范围在2.6–15之间[23]. 如果我们取其平均值, 则可以得到双黑洞轨道半径R ～8.3×1016cm (～0.03 pc), 说明3C 66A中的双黑洞已经演化到了“最后1 pc”阶段(0.01–1 pc)[44].

除此之外, 螺旋结构的喷流模型也会导致Blazar天体的周期性光变[45]. 由强磁场或轨道运动导致的扭曲喷流, 在视角改变时, 由于多普勒效应会使得观测的流量产生变化. 对于非均匀旋转螺旋喷流, 其中发射物质速度的方向与我们的视线夹角会周期性的变化. 由于多普勒增亮效应, 就会导致观测的流量周期性变化[46–47]. 3C 66A是Blazar天体, 其辐射流量主要来自于喷流中的非热辐射, 而甚长基线阵列(VLBA)观测发现其喷流呈现扭曲的形状[48], 所以其周期性光变也可能是螺旋喷流旋转造成的. 另外, 3C 66A同时也是BL Lac天体, 其中可能存在一个辐射效率很低的吸积盘[49], 而吸积盘的不稳定传递到喷流当中也会造成观测流量的周期变化[50].

致谢 我们感谢审稿人为本文提出的宝贵意见, 本文使用了AAVSO数据库和Steward天文台提供的开源数据.