高红移类星体的21 cm信号研究*
向宏斌 马清波
(1 贵州师范大学物理与电子科学学院 贵阳 550025)
(2 贵州省射电天文数据处理重点实验室贵州师范大学 贵阳 550001)
1 引言
类星体(QSO)是人类观测到的非常遥远且具有极高光度的天体, 是20世纪60年代天文学4大发现之一[1]. 研究发现QSO的中心位置存在一个超大质量黑洞[2], 一些QSO的中心黑洞质量甚至可达109倍太阳质量(M⊙)以上, 且吸积率接近爱丁顿极限[1], 因此高红移(z >6) QSO可以被光学或近红外望远镜直接观测[3]. 目前观测到z >6的QSO样本数量超过200颗[4–5], 而样本中z >6.5的QSO大约只有几十颗[6–7],z >7的QSO仅有6颗[8–13], 其中红移7.085的ULAS J1120+0641中心黑洞质量最大, 约2.0×109M⊙. 高红移QSO是研究宇宙再电离时期(Epoch of Reionization, EoR)的重要探针,冈恩- 彼得森槽(Gunn-Peterson trough)的观测发现宇宙星系际介质(Intergalactic Medium, IGM)的中性气体比例随红移增加而迅速提高, 表明宇宙再电离大概在z ~6时结束[14].
EoR时期的QSO辐射(紫外(UV)和X射线光子)会逐渐电离周围中性IGM, 并产生一个很大的HII区域(也称为电离泡或斯特龙根球区[15]), 而HII区外IGM中存在大量的中性氢. 中性氢原子的超精细结构跃迁辐射(波长λ= 21 cm, 频率ν=1.42 GHz)可被射电望远镜如低频射电阵列望远镜(Low Frequency Array, LOFAR)1http://www.lofar.org/、默奇森宽场阵列望远镜(Murchison Widefield Array, MWA)2http://www.mwatelescope.org/、氢原子再电离时代阵列望远镜(Hydrogen Epoch of Reionization Array, HERA)3https://reionization.org/、500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical Telescope, FAST) 和将建成的平方公里阵列射电望远镜(Square Kilometre Array, SKA)4https://www.skatelescope.org/等观测. 对单个高红移QSO产生的HII区以及21 cm辐射观测能提供高红移QSO的物理特性和中性氢比例等信息[16–17], 而由于HII区没有21 cm辐射, 因此也可以通过已知HII区来搜索高红移QSO[18]. 为此, White等[19]、Wyithe等[20]、Yu[15]和Majumdar等[21]建立了高红移QSO的HII区和21 cm辐射演化的理论解析模型,Feng等[22]、Kakiichi等[23]和Ma等[17]则利用高精度宇宙学数值模拟和辐射转移数值模拟进行了相同的研究. 相对于理论解析模型, 数值模拟能更精确地研究HII区和21 cm辐射的非线性特征, 但不利于研究模型参数空间.
本文将ULAS J1120+0641作为参考源, 结合高精度数值模拟结果[17,23]对理论模型[20]进行修正,并研究FAST望远镜观测高红移QSO的21 cm辐射的信号特征和信噪比. 第2节描述高红移QSO的HII区理论模型、数值模拟和21 cm信号的计算方法,第3节是研究结果, 第4节进行总结和展望. 本文引用宇宙学参数: 暗能量密度参数ΩΛ= 0.74、暗物质密度参数Ωm= 0.26、重子物质密度参数Ωb= 0.0463、无量纲哈勃常数h=h0/100 km·s-1·Mpc-1取值为0.72、标量谱指数ns= 0.95、物质涨落幅度参数σ8= 0.85[24],h0为哈勃常数.
2 QSO周围HII区和21 cm信号
2.1 节陈述了Yu[15]、Wyithe等[20]和Majumdar等[21]工作中高红移QSO电离和加热中性气体的理论解析模型, 2.2节描述了文献Kakiichi等[23]和Ma等[17]工作中使用的高精度流体动力学和辐射转移数值模拟, 2.3节介绍了如何利用2.1节和2.2节得到的电离和温度等信息计算21 cm亮温度.
2.1 理论模型
早期的相关工作如Yu[15]和White等[19]仅使用了简单的QSO电离模型, Wyithe等[20]进行了总结并增加了QSO加热中性气体的物理过程. 这里仅对模型进行简略总结, 具体内容如模型选择、参数设置等可参考Wyithe等[20]的工作.
由于电离光子如UV光子等的平均自由程较短,QSO对中性气体的电离过程由内到外逐渐进行. 假设QSO产生的电离光子均能电离中性氢, QSO电离产生的HII区的物理半径(Rp)随时间的演化方程为:
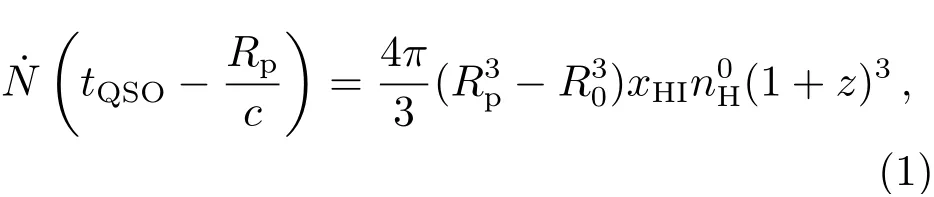
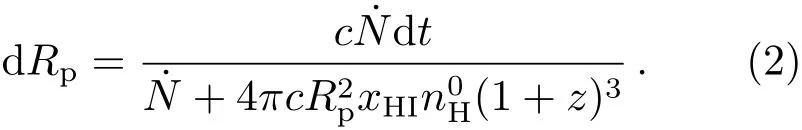
通过解方程(1)式或对(2)式进行数值积分可计算得到QSO周围HII区的物理半径随时间的演化. 这里假设HII区和HI区之间的边界很薄, 电离光子可以通过HII区直接到达HI区, 从而完全电离边界区域的中性氢.
相对于电离辐射如UV光子,更高能辐射如X射线光子等的平均自由程较长, 能有效地穿过电离区并加热中性气体. 当物理半径大于电离半径即R >Rp时, QSO辐射的高能光子穿过电离边界开始加热中性气体, 加热率ΓX(单位erg·s-1·Mpc-3)为[20]:
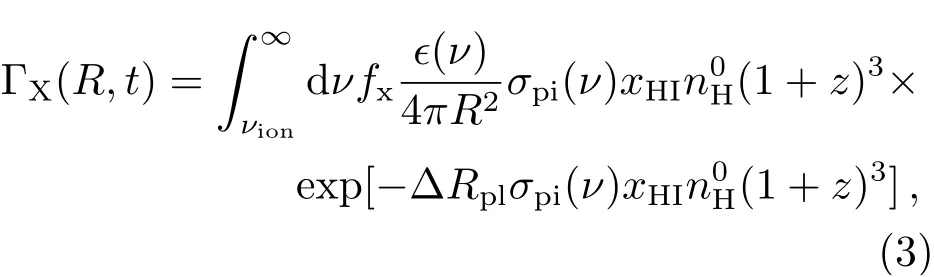
式中,νion= 3.29×1015Hz是电离光子的最小频率,fx是光子能量转换为气体热能的比例,ϵ(ν)为QSO光谱,σpi(ν)是光子散射的横截面积, ΔRpl=R-Rp(t-Δt)是到达半径R处的高能光子在时间t时穿过HI区的长度. IGM气体温度(TIGM)则可由下式计算:
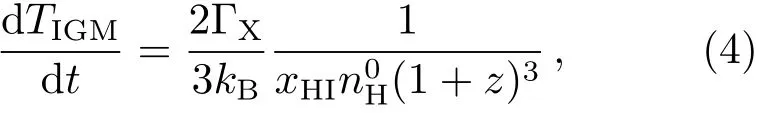
式中kB是玻尔兹曼常数.
2.2 数值模拟
Kakiichi等[23]和Ma等[17]使用高精度宇宙学流体动力学(使用GADGET-3程序[25])和辐射转移(使用CRASH程序[26–28])数值模拟研究了高红移QSO对中性气体的电离(xHI)和加热(TIGM)效应. 其中Kakiichi等[23]详细分析了高红移QSO对宇宙中IGM气体的密度、电离度和温度分布的影响, Ma等[17]计算了高红移QSO周围的21 cm信号, 并预测了SKA低频(SKA1-low)望远镜观测此类信号的可行性. 这些数值模拟包含了3维宇宙学N体、流体动力学以及多频辐射转移数值模拟, 覆盖了UV和X射线波段(13.6–2000 eV)辐射以及二次电离过程, 是目前研究高红移QSO电离和加热效应较为精确的数值模拟. 数值模拟的具体内容和结果可参考Kakiichi等[23]和Ma等[17]的工作, 这里仅做简略总结.
该数值模拟的尺度为50h-1·cMpc (cMpc为comoving Mpc), 含有2×5123个暗物质和气体粒子, 其中暗物质粒子的质量为MDM= 5.53×107h-1M⊙、气体粒子质量为Mgas= 1.20×107h-1M⊙. 辐射转移数值模拟开始于z= 15,在z >10仅有恒星源贡献气体的电离度, 其电离光子产生率(单位为photon·s-1)与暗物质晕的质量Mhalo成线性关系:
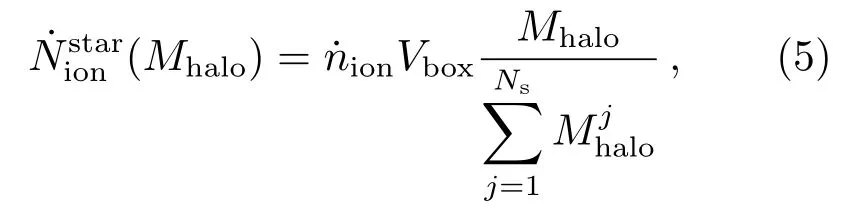
式中Ns是数值模拟得到的暗物质晕总数目,Vbox是数值模拟的体积,是第j个暗物质晕的质量, 电离光子效率= 0.72×1050photon·s-1·cMpc-3.的取值主要考虑了宇宙微波背景辐射(Cosmic Microwave Background, CMB)不透明度的观测对再电离模型的限制[23]. 发光QSO假设存在于数值模拟得到的最大暗物质晕(Mhalo=1.34×1010h-1M⊙)中心, 并在红移z= 10开始产生辐射. QSO光谱依据z= 7.085的QSO ULAS J1120+0641的观测结果, 但假设更高红移(z= 10) QSO的光度仅有ULAS J1120+0641的0.1倍,即,其电离光子数~1.36×1056photon·s-1.
2.3 21 cm信号
利用理论解析模型公式(2.1节)或数值模拟(2.2节)得到的气体密度、电离度和温度等信息, 可计算中性氢21 cm辐射的亮温度(Differential Brightness Temperature, DBT)[29]:
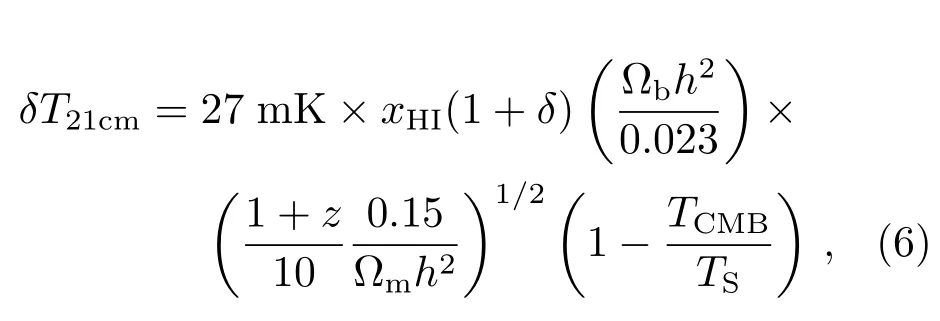
式中δ是气体物质的相对密度,TCMB是宇宙微波背景辐射温度,TS是中性氢的自旋温度. 由于QSO主要存在于宇宙再电离的中期和晚期, 这里假设中性氢自旋温度等于星系际介质温度, 即TS=TIGM.
考虑到辐射光子的有限旅行时间(Finite Light Travel Time, FLTT)效应[20–21,30], QSO周围快速增长的HII区对于地球上的观测者来说可能呈现各向异性.
如图1所示, O代表观测者, 圆形虚线表示某一时刻QSO周围HII区的大小. 由于在视线方向上QSO左侧的HII区边界上的光子比QSO本身辐射的光子需要更多的时间到达观测者, 因此在同一时刻观测者实际观测到的左侧HII区的年龄要小于QSO的年龄. 而右侧HII区边界上的光子比QSO本身辐射光子到达观测者的时间要短, 因此实际观测到的右侧HII区的年龄要大于QSO的年龄. 综合两种情况, 在同一时刻观测者观测到的QSO周围HII区的轮廓大致如实线所示. Ma等[17]的研究结果表明该效应明显影响QSO的21 cm观测结果, 但对普通星系的影响较弱, 因此计算QSO周围21 cm信号需要对理论模型或数值模拟的结果进行修正:
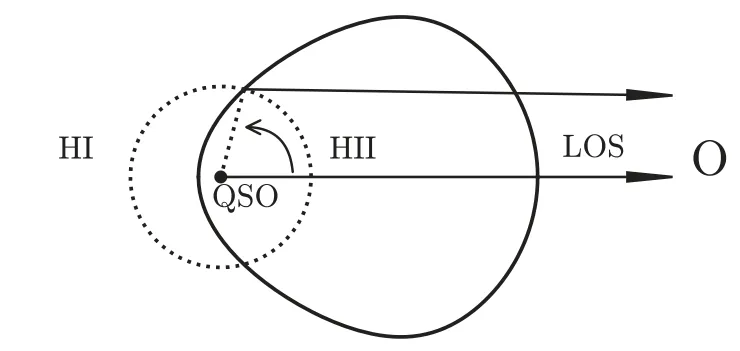
图1 QSO周围HII区的观测受FLTT效应影响的示意图, 其中LOS(Line Of Sight)为视线方向, β为HII边界与视线方向的夹角.Fig.1 Diagram of FLTT effect on the observation of HII region around QSO, where LOS denotes line of sight, β is the angle between LOS and HII frontier.
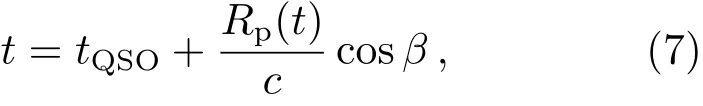
(7)式中Rp依赖于时间t, 即更早或者更晚时的QSO年龄.
3 结果
基于第2节陈述的理论解析模型和数值模拟结果, 3.1节将比较分析理论计算和数值模拟结果的异同, 并利用高精度数值模拟的结果修正理论解析模型, 3.2节利用修正后的模型预测FAST观测高红移QSO周围21 cm辐射的信号特征和信噪比.
3.1 21 cm信号
图2是数值模拟(2.2节)得到的QSO年龄tQSO=1、5、10 Myr时周围的21 cm亮温度分布图像. 考虑到高红移高能辐射源在理论和观测上的不确定性[17], 假设两种情形: (1)z= 10时仅有QSO加热中性IGM气体, 即中性氢的自旋温度TS=TIGM;(2)z= 10时中性IGM气体已被其他高能辐射源如X射线双星、高温星际介质等[31]加热, 即自旋温度TS≫TCMB. 从图2 可看出, QSO辐射在较短时间内(10 Myr)快速增大周围的HII区, 且中性气体被有效加热, 因此在TS=TIGM情形下有较大半径内的中性氢21 cm辐射为发射线. 在TS≫TCMB情形下, 中性氢仅有21 cm发射线, QSO仅增加了HII区的大小.
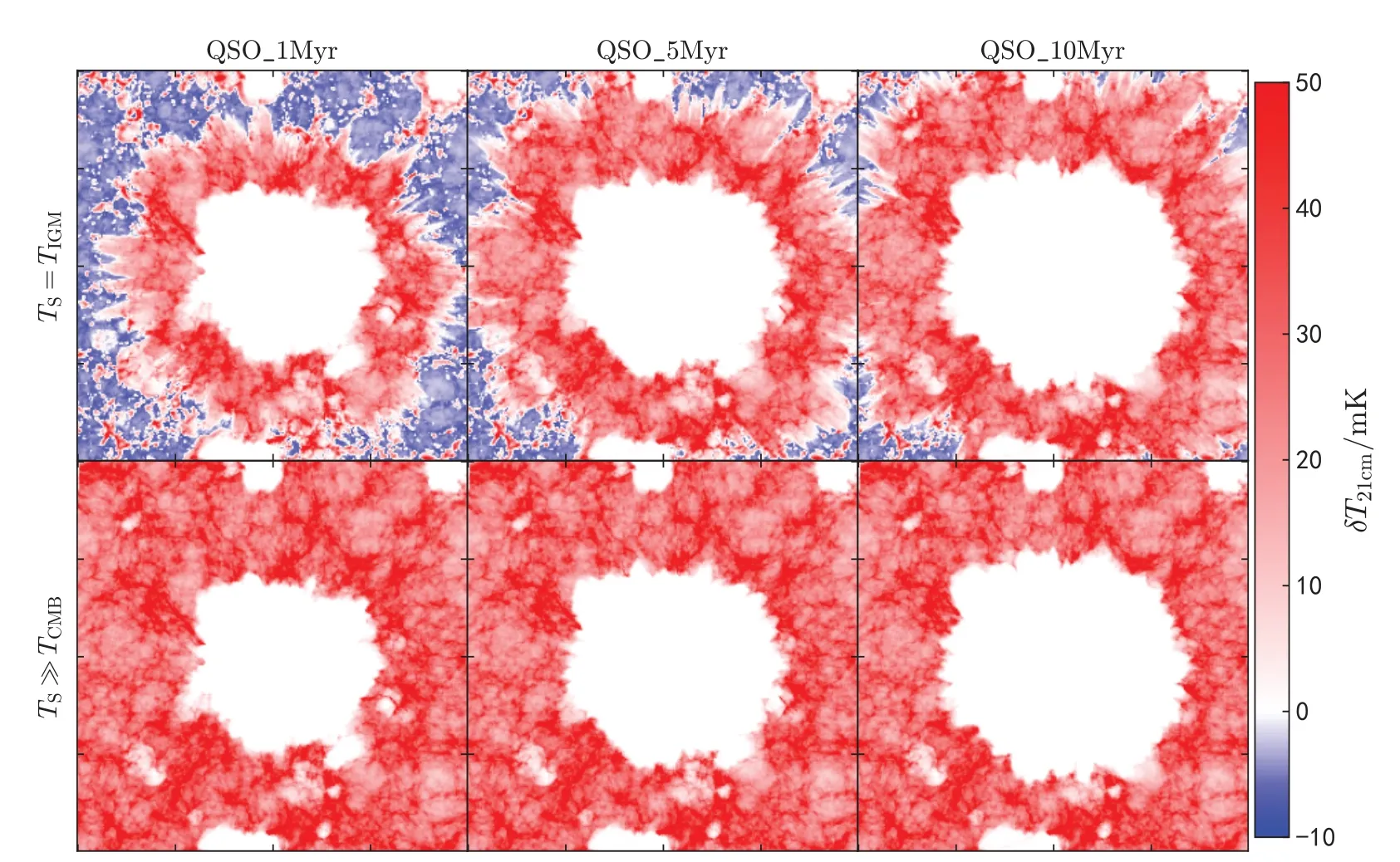
图2 TS = TIGM (上图)和TS ≫TCMB (下图)情形下的21 cm亮温度图像. 从左至右QSO年龄分别是tQSO = 1、5、10 Myr.Fig.2 21 cm DBT images with TS = TIGM (upper panels) and TS ≫TCMB (lower panels). From left to right, the QSO age tQSO = 1, 5 and 10 Myr.
如图3所示, 是21 cm亮温度以角半径为变量的1维统计(即球面平均)函数. 从图3可以更清晰看出QSO对周围HII区和21 cm发射信号的影响. 在TS=TIGM情形下, QSO在短时间内不仅增加了HII区的半径, 如tQSO= 1 Myr时HII区角半径θ仅有3.6′, 而在tQSO= 5和10 Myr时角半径θ分别有4.2′和4.7′, 同时明显增大了21 cm发射区域的角半径. 在TS≫TCMB情形下, QSO的存在仅表现为HII区半径的增加, 外围的21 cm辐射没有明显变化.
图3的 细 线 是 理 论 解 析 模 型(2.1节)给 出的21 cm亮温度分别在QSO年龄tQSO= 1、5、10 Myr时以角半径为自变量的函数. 由于数值模拟中包含了恒星源的贡献, 在QSO开始贡献辐射前IGM中的中性氢已被部分电离且QSO周围已存在一个小的由星系自身辐射电离的HII区, 因此理论模型中的参数根据数值模拟的结果进行了微调,如中性氢比例xHI设为0.88,tQSO= 0时HII区的半径R0= 1.1 Mpc. 考虑到数值模拟[23]中包含了高能光子的二次加热效应, 即有更多的光子能量转化为气体热能, 设光子能量转为气体热能的比例fx=0.35. 此外由于数值模拟未考虑光速有限性, 因此也忽略了(1)式中的Rp/c项. 该项会对QSO的年龄估计有一定影响, 但对21 cm的观测结果没有明显影响. 从图3可看出理论模型能较好地计算QSO周围HII区的半径, 且在TS≫TCMB情形下与较大θ处的21 cm亮温度符合较好, 在TS=TIGM情形下仅与tQSO=10 Myr时部分θ处的21 cm亮温度符合较好.

图3 TS = TIGM (左)和TS ≫TCMB (右)情形下21 cm亮温度以角半径为自变量的1维统计函数. 红色虚线、青色虚点线、蓝色点线分别表示QSO年龄tQSO = 1、5、10 Myr. 数值模拟和理论模型结果分别以粗线和细线表示.Fig.3 1-D statistics of 21 cm DBT as functions of angular radius with TS = TIGM (left) and TS ≫TCMB (right). Red dashed,cyan dash-dotted, and blue dotted lines denote tQSO = 1, 5 and 10 Myr, respectively. The results of numerical simulations and theoretical models are with thick and thin lines, respectively.
造成理论模型和数值模拟结果差异的主要原因有: (1) 3维数值模拟考虑了气体密度和辐射的不均匀性(如图2所示), 即QSO周围的HII区存在各向异性, 因此完全电离区到中性区之间存在过渡区域; (2)数值模拟考虑了激波加热效应, 因此QSO加热前部分气体已有较高温度. 对于电离区到中性区之间存在的过渡区域, 可使用sigmoid函数进行修正, 即在(6)式的基础上增加函数:
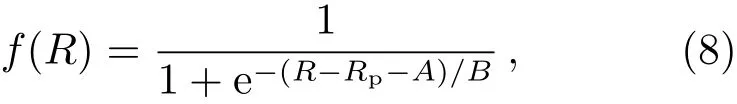
式中参数A、B是QSO年龄tQSO的线性函数.
图4是理论模型修正后的21 cm亮温度随角半径变化的函数. 在TS≫TCMB情形下, 修正后的理论模型结果在3个QSO年龄上都与数值模拟的结果符合得很好. 在TS=TIGM情形下, 修正后的理论模型在tQSO= 10 Myr与数值模拟符合很好, 而在tQSO= 1、5 Myr时21 cm亮温度明显低于数值模拟结果. 这是因为激波加热效应对QSO早期(即加热效应较弱)的效果明显, 而在QSO显著加热中性气体(即较晚期)时其效应可忽略不计. 总体上看,修正后的理论模型能在很大程度上符合高精度流体动力学和辐射转移数值模拟的结果.
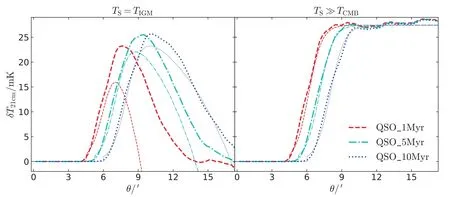
图4 理论模型修正后的21 cm亮温度在TS = TIGM (左)和TS ≫TCMB (右)情形下以角半径为自变量的函数. 红色虚线、青色虚点线、蓝色点线分别表示QSO年龄tQSO = 1、5、10 Myr. 作为参考, 数值模拟的结果以粗线条表示.Fig.4 21 cm DBT results of fixed theoretical models as functions of angular radius, with TS = TIGM (left) and TS ≫TCMB(right). Red dashed, cyan dash-dotted, and blue dotted lines denote tQSO = 1, 5 and 10 Myr, respectively. As a reference, the results of numerical simulations are presented with thick lines.
3.2 FAST观测QSO的21 cm信号
FAST5FAST望远镜参数来自网站https://fast.bao.ac.cn是目前世界上最大的单天线射电望远镜, 其有效口径~300 m, 灵敏度S= 2000 m2·K-1[32–34]. FAST观测21 cm亮温度的仪器噪声[17]:
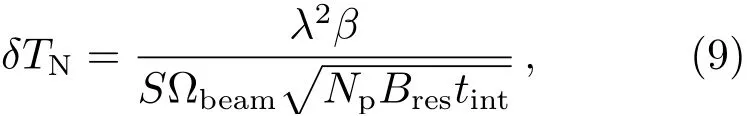
式中,λ ~0.21 m×(1+z)是红移z处21 cm辐射的观测波长, 数字化损失参数β= 1.5, 观测立体角Ωbeam= 1.133ϑ2,ϑ= 2.9′ ×(1+z)是FAST在红移z处的角分辨率,Np=1是观测望远镜的个数, 频率分辨率Bres假设为0.1 MHz, 积分时间tint假设为3600 s. 虽然FAST的角分辨率较低(在红移z= 10仅有31.9′), 无法有效观测QSO产生的3维21 cm图像, 但较高的频率分辨率有助于研究其在视线方向上的分布特征, 因此本节将利用第3.1节修正后的理论模型研究FAST观测QSO周围21 cm辐射的信号特征以及信噪比. 此外, 为了简化讨论, 假设QSO年龄tQSO= 10 Myr, 并假设21 cm辐射的前景污染和QSO自身的射电辐射可通过模型完全扣除[35–36].
如图5所示, 左侧是FAST观测z= 10 QSO的21 cm信号和信噪比. 由于FAST的角分辨率较低,z= 10 QSO周围的HII区无法被望远镜单独观测, 因此观测到的21 cm信号在TS≫TCMB情形仅有一个较浅的凹陷, 其在QSO的位置(ν=130.9 MHz)有最小值~13.6 mK. 在TS=TIGM情形下观测到的21 cm信号存在两个鼓包, 分别在ν~130.4 MHz和132.3 MHz. 左侧的鼓包距离QSO较近并且幅值偏小, 右侧的鼓包距离QSO较远但幅值偏大, 这是FLTT效应产生的典型观测结果.
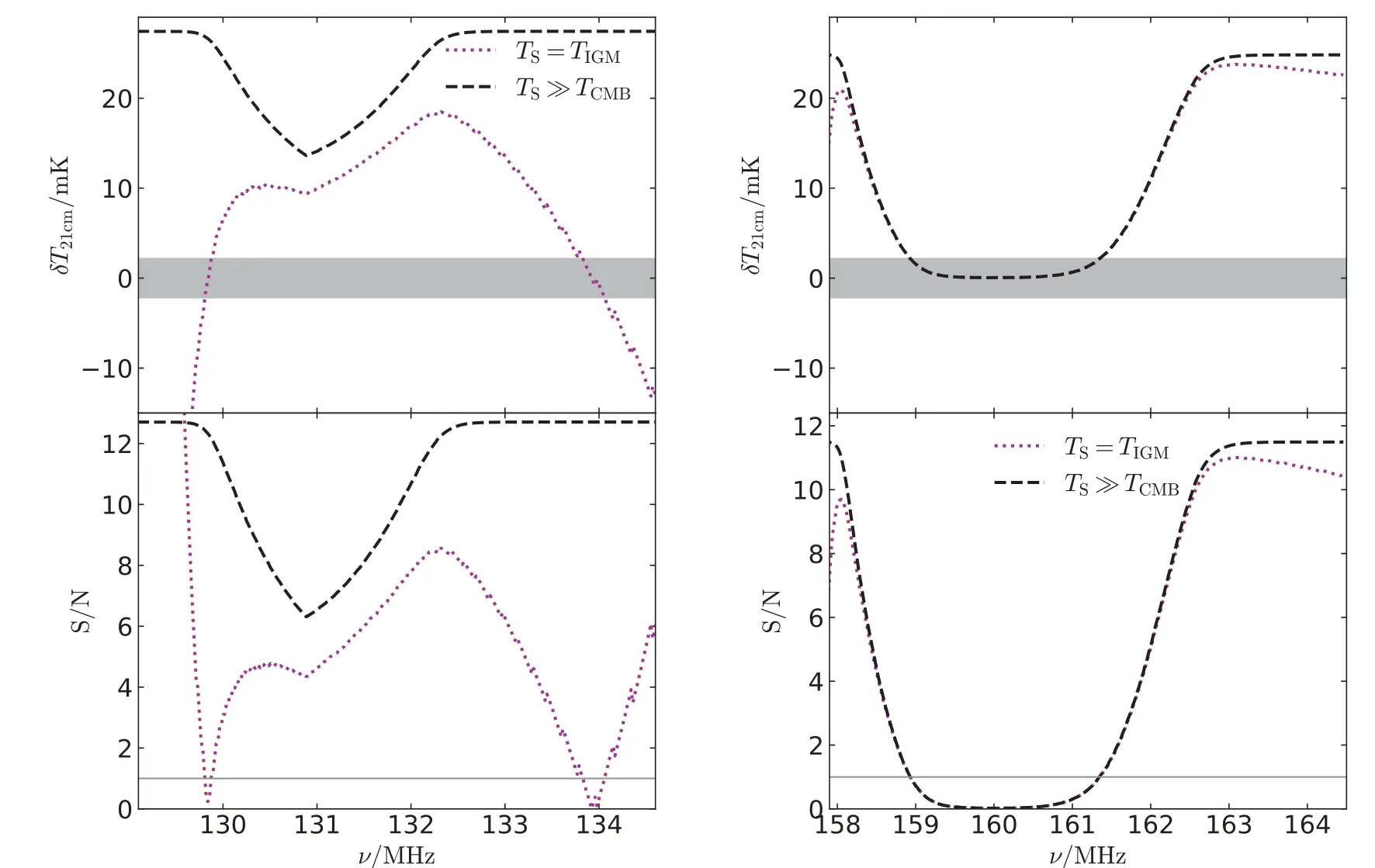
图5 FAST观测红移z = 10 (左)和8 (右)的QSO在频率ν方向上的21 cm信号(上)和信噪比(下). 紫红色点线和黑色虚线分别表示TS = TIGM情形和TS ≫TCMB情形. 上图的灰色部分是低于FAST噪声的区域, 下图的灰色实线表示S/N = 1.Fig.5 21 cm DBT (upper) and S/N (lower) of QSO at z = 10 (left) and 8 (right) versus frequency ν, which measured by FAST.Magenta dotted and black dashed lines denote TS = TIGM and TS ≫TCMB, respectively. The gray regions in the upper panels are those lower than FAST noise level, while the gray lines in the lower panels denote S/N = 1.
考虑到z= 10的QSO模型采用的光度较低(仅有ULAS J1120+0641的0.1倍), 因此利用修正后的理论模型计算了FAST观测z= 8且光度和ULAS J1120+0641一致的QSO周围的21 cm辐射和信噪比. 如图5右图所示,z=8处QSO产生的HII区可以被FAST完全观测, 因此在TS≫TCMB情形下FAST将观测到一个完整的由超亮QSO产生的HII区, 并且其左侧由最大值到0的过渡曲线明显比右侧由0到最大值的过渡曲线偏陡. 在TS=TIGM情形下的观测结果与TS≫TCMB情形相似, 但在左侧最大值之前的21 cm亮温度幅值会快速下降并变为吸收信号, 而在右侧过渡缓慢, 将能在很大频率范围内观测到21 cm的发射信号.
FAST噪声远低于大部分ν处的21 cm吸收和发射信号, 因此FAST将能够以很高的信噪比观测高红移QSO周围的21 cm信号, 其发射信号的信噪比最高~12, 将能很好地识别HII区和FLTT效应. 需要注意的是, 计算采用的灵敏度(即S= 2000 m2·K-1)是FAST在中频波段(~1.5 GHz)的数值, 预计在低频波段的灵敏度可能会低于该数值. 在未来的实际观测中, 可考虑增加探测器数目或者观测时间来提高信噪比. 此外, 未来“天眼阵列”的建设也能在很大程度上提高观测信噪比.
4 总结与展望
在对高红移QSO的21 cm辐射研究中, 本文结合高精度数值模拟的结果[17,23]对理论模型[20]进行了修正, 并预测了FAST望远镜观测高红移QSO的21 cm辐射的信号特征和信噪比. 考虑到EoR高能辐射源的不确定性, 假设了两种不同的中性氢自旋温度情形, 即(1)仅有QSO加热中性IGM气体TS=TIGM和(2)在QSO辐射前中性气体已被其他辐射源加热TS≫TCMB. 考虑了光子有限旅行时间效应[20–21,30]对FAST望远镜观测结果的影响, 并预测了两个红移和两个QSO模型下的FAST观测结果. 我们发现:
(1)在TS≫TCMB的情形下, 修正后的理论模型在多个QSO年龄(tQSO= 1、5、10 Myr)上都与高精度流体动力学和辐射转移数值模拟的结果相符. 在TS=TIGM情形下,虽然没有包含激波加热效应, 但修正后的理论模型依然能较好地符合QSO高年龄(tQSO= 10 Myr)的数值模拟结果;
(2)由于FAST望远镜的角分辨率较低, 在红移z= 10且QSO低光度模型下, FAST视场中的21 cm亮温度仅在ν= 130.9 MHz处有一个较浅的凹陷, 最小值~13.6 mK. 在z= 8且光度和ULAS J1120+0641一致的QSO模型下, FAST视场中的21 cm亮温度频率谱有完整的HII区;
(3)通过FAST观测到的21 cm亮温度在频率方向上明显受到FLTT效应的影响, 如在z=10以及TS=TIGM情形下, 21 cm亮温度在ν ~130.4 MHz和132.3 MHz处有鼓包, 前者距离QSO较近但幅值较小, 后者距离QSO较远但幅值较大. 在z= 8处,频率较低端的过渡曲线明显比频率较高一端偏陡;
(4)假设FAST望远镜在低频波段与中频波段的灵敏度相同即2000 m2·K-1, FAST望远镜能以很高的信噪比观测QSO周围的21 cm信号, 其信噪比最大值为~12, 因此FAST望远镜将能很好地观测QSO的HII区以及FLTT效应.

