基于SIFT特征检测和密度峰值聚类的太阳活动区自动检测算法研究*
蒋 博 刘 磊 郑 胜 杨珊珊 曾曙光 黄 瑶 罗骁域
(三峡大学天文与空间科学研究中心 宜昌 443002)
1 引言
太阳表面存在各种不同的活动现象, 它们与太阳大气中磁场的分布和位形密切相关, 涉及等离子体的加热和运动、电磁辐射的增强、高能粒子的加速和波动等各种物理过程[1]. 太阳黑子是太阳表面最基本的活动现象, 黑子的多少表征着太阳活动程度的高低, 由黑子组成的活动区是太阳爆发(太阳耀斑和日冕物质抛射)的源区. 它驱动着太阳活动, 对近地空间、行星际和日球环境有着极为重要的影响[2]. 因此, 对于太阳活动区域进行准确的识别是一项重要的工作[3].
太阳活动区的检测是一种典型的多目标检测问题,已有很多学者对太阳活动区的检测进行研究.早期的检测通常采用经典的图像处理技术, 例如阈值分割法[4]、区域生长法[5–6]等, 但是这些方法的检测效果强烈依赖于强度阈值和区域生长的边界阈值等参数的设置[7]. Zhang等[8]提出的自动图像处理与机器学习相结合的自动检测算法会因为活动区的重叠导致无法正确聚类. Caballero等[9]提出的与极紫外成像望远镜和日光层天文台航天器相结合的自动检测系统以及Higgins等[5]提出的使用SOHO (Solar and Heliospheric Observatory)迈克尔逊多普勒成像仪(Michelson Doppler Imager,MDI)与太阳监测器活动区域跟踪(The Solar Monitor Active Region Tracking, SMART)算法相结合的自动检测系统均容易导致多个相邻的太阳活动区被误检测为一个或一个太阳活动区被误检测为多个. 近年来, 人工智能在天文学上的应用与日俱增. 例如, 朱健等[10]基于YOLOv3 (You Only Look Once)和DeepSort算法对太阳活动区进行的检测和跟踪, 采用16361个太阳活动区样本进行训练, 达到了92%的检测准确率. LeNet-5以及AlexNet等卷积神经网络也被广泛地用于天文学研究中[11–12]. 这些人工智能方法在天文学研究中虽然有着较高的准确率, 但是需要提前对大量样本数据进行训练与测试后才能使用.
尺度不变特征变换(Scale-Invariant Feature Transform, SIFT)是一种基于局部描述子的特征点检测方法, 对于光线、噪声、视角改变的容忍度相当高[13–14], 对于含有许多内部结构、特征点较明显的太阳磁场图像具有较好的检测效果.2018年,杨盼等[15]采用SIFT算法将怀柔太阳观测基地的局部太阳磁场图像与日震和磁像仪(Helioseismic and Magnetic Imager, HMI)的全日面太阳磁场图像进行配准与定位. 近年来, 聚类算法被广泛地应用在目标识别中. 其中, 密度峰值聚类(Clustering by Fast Search and Find of Density Peaks, DPC)算法是一种基于数据点密度进行自动分类的聚类算法[16]. 该算法基于聚类中心拥有较高的密度及聚类中心点之间距离较大两个假设, 能够直观地得到聚类的个数、自动地发现聚类中心并且能排除异常点同时不受聚类对象嵌入空间维数的限制, 实现任意形状数据的高效聚类.
本文针对太阳活动区结构较为复杂的特点, 采用SIFT特征提取算法提取太阳活动区的特征点,利用密度峰值聚类算法对提取的特征点进行聚类,实现了太阳活动区的自动检测. 该算法可以在不需要人工交互的情况下有效检测并识别太阳活动区.
2 检测算法原理
SIFT和DPC算法主要原理如下.
2.1 SIFT算法
SIFT是一种计算机视觉的算法. 它用来侦测与描述影像中的局部性特征, 它在空间尺度中寻找极值点, 并提取出其位置、尺度、旋转不变量, 此算法由Lowe在1999 年发表[14],2004年完善总结[13].该方法步骤如下:
(1)尺度空间的生成
尺度空间的理论方法是检测特征不变性的主要基础. 尺度空间理论的目的是模拟图像的多尺度特征, Koenderink[17]证明了高斯核函数是实现尺度变换的唯一变换核. 二维图像与高斯核函数的卷积可以得到该图像在不同尺度下的尺度空间L(x,y,σ).
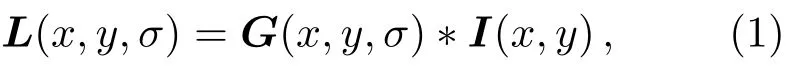
式中,x、y为像素坐标,I(x,y)为灰度值,G(x,y,σ)为高斯核函数,σ是高斯正态分布的方差. 高斯核函数的定义如下:
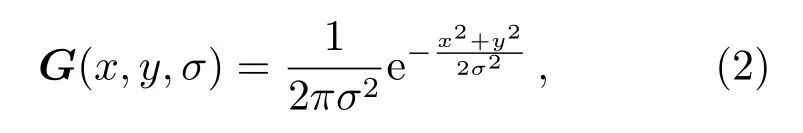
其中, 正态分布方差σ在图像中叫做尺度空间因子,它反映了图像被平滑的程度, 尺度越小表示图像被平滑得越小, 对应于图像的细节特征, 大尺度对应于图像的概貌特征.
(2)检测尺度空间的极值点
为高效地在尺度空间检测出稳定的极值,Lowe[13]使用尺度空间中差分高斯DOG的极值作为判断依据. DOG算子定义如下:
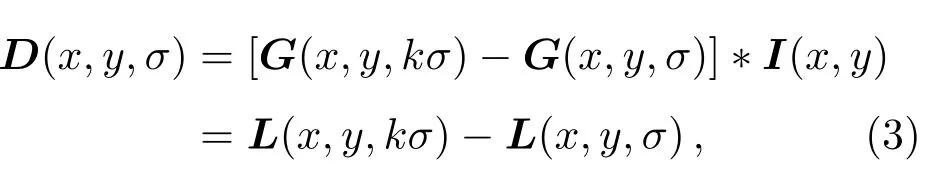
其中,k是相邻两个尺度空间的比例因子.
为了确保特征点的稳定性和匹配准确性, 对SIFT候选点集进行筛选, 去除其中对比度低的特征点与图像边缘的特征点, 增强匹配的稳定性. 以上两步骤的示意图如图1所示.

图1 尺度变换与极值点检测[14]Fig.1 Scale transformation and extreme detection[14]
(3)计算方向幅值
为了区分不同关键点的属性, 可以利用其邻域像素的梯度变化特性来计算关键点附近各个方向的方向幅值, 并绘制该关键点附近的方向累积直方图, 其中幅值累积最大的方向为特征点的主梯度方向.
(4)关键点描述
以关键点周围8×8的窗口为例, 将坐标轴旋转为主梯度方向, 计算关键点周围8×8的窗口中每一个像素的梯度, 并且使用高斯下降函数降低远离中心的关键点的权重. 这样就能生成一个2×2×8= 32维的描述子, 每一维都可以表示2×2格子中的一个梯度的方向与尺度大小特征, 如图2所示.
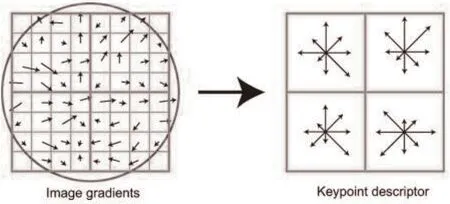
图2 生成关键点描述子示意图[14]Fig.2 Generate the keypoint descriptor[14]
2.2 密度峰值聚类
基于DPC算法可以识别任意大小、形状的聚类对象, 同时可以有效地滤除噪声[16]. DPC算法2014年发表在Science杂志上, 使得基于密度的聚类方法取得质的飞跃. DPC的核心思想是认为聚类中心的密度显著大于其邻域内其他点的密度, 且聚类中心之间的距离相对较远. DPC的有效检测建立在两个假设上: (1)聚类中心被局部密度较低的点包围; (2)聚类中心点与其他聚类中心点的距离相对较大. DPC算法的步骤如下.
(1)使用截断核(Cut offkernel)计算每个点的密度ρi:
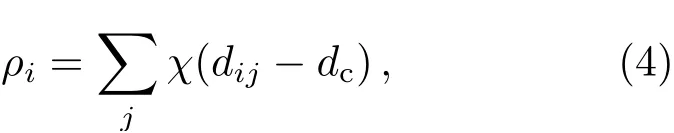
(2)根据每个数据点周围一定范围内数据点的数量, 计算得到数据点的密度{ρ1,ρ2,··· ,ρn},n为点数, 并对其进行排序, 计算每个点的距离δi:
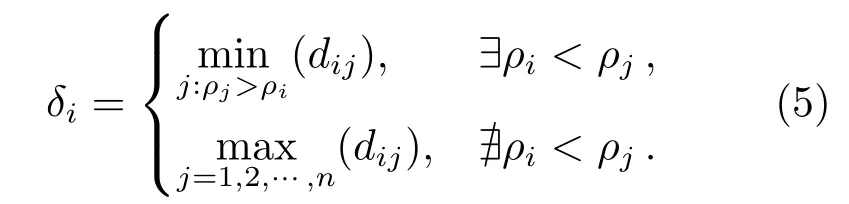
当存在密度高于当前数据点的数据点时, 当前数据点的距离为比该点密度大的所有数据点距离的最小值. 其中, 密度最大的数据点的距离指定为所有数据点中距离最大值.
(3)通过设定密度和距离的阈值, 选取聚类中心点. 根据非类中心和类中心之间的距离, 将其他非类中心点分配到距离最近的聚类中心点, 从而完成聚类.
3 算法设计及实验分析
本文采用的观测数据来自于太阳动力学天文台(Solar Dynamics Observatory,SDO)上HMI的全日面纵向磁图[17–18]. 实验使用的所有全日面图像数据从http://jsoc.stanford.edu/ajax/lookdata.html网站上以fits格式下载, 将每张样本图像转换成2048×2048像素的JPG图像, 使用SIFT和DPC算法相结合的方法来实现太阳活动区的自动检测, 实验流程及结果如下.
3.1 算法设计
基于SIFT与DPC的太阳活动区自动检测算法流程图如图3所示, 具体步骤如下:
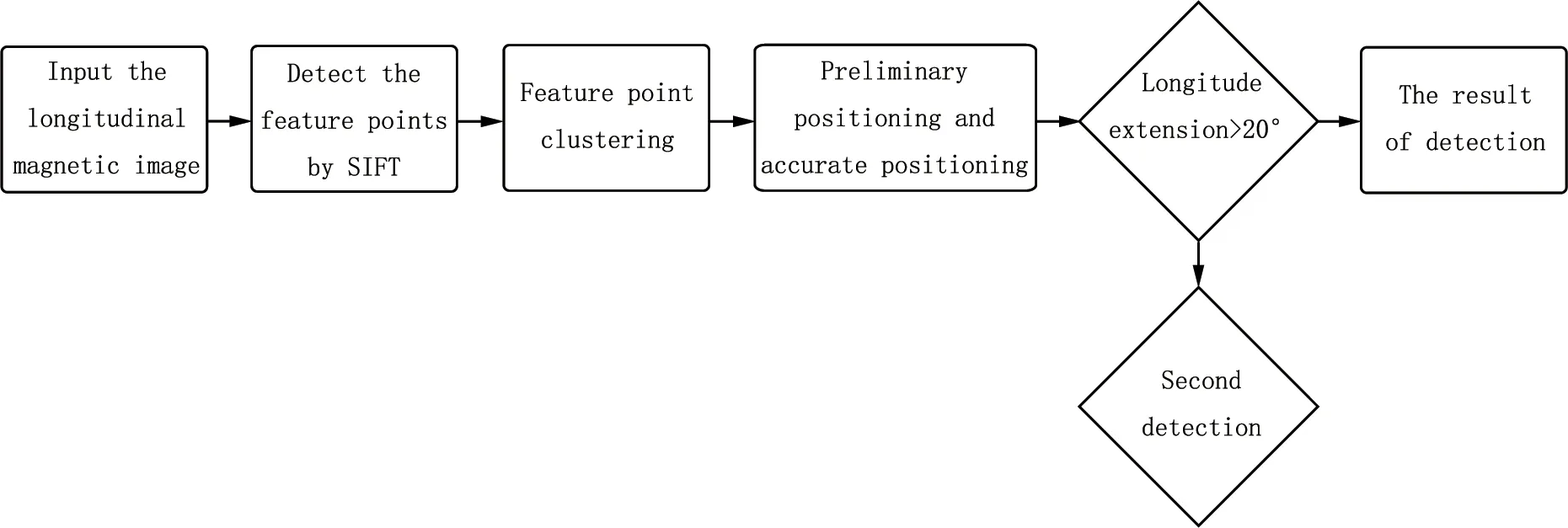
图3 太阳活动区自动检测算法流程Fig.3 Flow chart of solar activity regions automatic detection
(1)图像预处理, 对原始太阳磁场图像进行对比度增强, 增强活动区的特征信息;
(2)基于SIFT算法, 对增强后的图像进行特征点提取, 获得该全日面特征点集, 根据拍摄时间, 将特征点的像素坐标转化为经纬度坐标;
(3)对提取出来的特征点进行密度峰值聚类,根据特征点的密度分布与特征点相互间的距离特征, 可自动将特征点聚类;
(4)根据聚类决策图, 采用一定的判据(经统计,聚类中心点的密度需大于所有特征点密度的均值减0.5倍方差,距离需大于所有特征点距离的均值加3倍方差, 且该特征点在决策图上到坐标原点的距离需大于决策图对角线长度的一半)选出候选区域,完成太阳活动区的初步定位;
(5)基于最大类间方差法[19]对初步检测结果进行自动图像分割, 再用面积滤波去除噪声之后, 获取所得活动区的最小外接矩形, 即可完成对太阳活动区的精确定位;
(6)对日面经度延伸较大(例如大于20°)的活动区进行二次检测, 根据二次检测决策图, 采用二次聚类的判据(经统计, 聚类中心点的密度需大于所有特征点密度的均值加方差, 距离需大于所有特征点距离的均值加6倍方差)对其进行判别. 此时, 如果满足上述判据的特征点数量为2, 则需根据磁通量进一步判断, 若两特征点对应区域中均只含有一种极性, 且这两区域的极性相反, 则它们为同一活动区; 反之, 则应划为两个活动区.
3.2 实验结果与分析
根据上述算法思想, 我们编写了太阳活动区检测程序. 实验结果如下, 图4 (a)是2017年1月24日的全日面磁图, 图4 (b)显示的是对其进行对比度增强后的结果.

图4 原始太阳图像与预处理结果. (a)原始图像; (b)预处理结果图像.Fig.4 The original image and image after preprocessing. (a)The original image; (b) image after preprocessing.
然后, 使用SIFT算法提取增强后磁场图像的特征点, 结果如图5所示. 在这张图中我们总共检测到了1427个特征点, 可以看出在太阳活动区周围的特征点分布较为集中, 显著多于宁静区的特征点,检测结果很好地代表了太阳活动区的特征, 为下一步利用聚类算法进行活动区检测提供了基础.

图5 SIFT算法检测到的特征点分布Fig.5 The distribution of feature points detected by the SIFT algorithm
图6 展示了上述1427个特征点的密度峰值聚类结果图. 图6 (a)为密度峰值聚类决策图, 其横坐标ρ为特征点归一化后的密度, 纵坐标δ表示特征点和离它最近且密度大于该点的特征点之间归一化后的距离. 因此特征点在决策图中的位置越靠近右上, 表示该点越靠近聚类中心, 反之亦然. 通过统计分析, 我们发现太阳活动区的聚类中心应满足条件: (1)密度大于所有特征点的密度均值减0.5倍方差; (2)距离大于所有特征点的距离均值加3倍方差;(3)距离坐标原点的距离大于对角线长度的一半,即. 在图6 (a)的DPC决策图中, 所有特征点的密度均值为0.26, 密度方差为0.23, 距离均值为0.03,距离方差为0.07; 相应的密度判据为0.145, 距离判据为0.24, 距离原点的距离判据为满足上述判据的特征点一共有两个, 在图6 (a)中分别用蓝色和青色方框加以了标注. 由此可以判断出该磁场图像中的特征点有两个聚类中心. 图6 (b)为特征点的聚类结果图, 其中Dim1与Dim2分别表示图像的横纵坐标(单位为像素). 在该图中, 聚类算法将该图像的特征点自动分为了两类, 聚类中心分别用深蓝色和浅蓝色菱形加以标注; 右边红色点区域为第1类, 左边黑色区域为第2类, 绿色点区域为噪声.
根据该聚类结果在全日面磁图中的像素位置,可实现对太阳活动区在全日面磁图中的初步定位.对初步定位的结果, 使用最大类间方差[19]进行图像自动分割, 并使用面积滤波去除噪声, 即可获得太阳活动区的精确定位. 对全日面磁图的太阳活动区检测结果如图7所示, 其中蓝色虚线框是对太阳活动区初步定位的检测结果, 红色实线框是对太阳活动区精确检测的结果.

图7 密度峰值聚类算法检测结果Fig.7 The results of the proposed algorithm
为验证算法的有效性, 我们对不同时间拍摄的全日面太阳磁图进行了检测, 图8是部分太阳磁图的检测结果, 其中, 图8 (a)日面上仅存在一个太阳活动区, 图8 (b)日面上有3个太阳活动区. 结果表明, 无论全日面太阳磁图中存在单个或是多个太阳活动区, 该算法均能够有效地检测出太阳活动区.

图8 不同时间太阳磁场图像的自动检测结果Fig.8 The results of automatic detection for different solar magnetic field images
当两个活动区位置相近时, 有可能会产生误检, 即相近区域的两个活动区被误检为一个活动区. 为进一步提高检测准确性, 我们提出了对误检区域进行二次检测的方法. 对精确定位的结果进行检测, 若日面经度延伸大于20°, 则判定该区域可能存在两个活动区. 通过对提取出的误检区域使用SIFT算法与密度峰值聚类的二次检测, 可实现对误检区域的修正, 检测出正确的太阳活动区. 从而有效解决将多个活动区误检为一个活动区的问题,提高检测的准确性.
图9展示了本文方法与区域生长法的对比结果图. 图9 (a)是本文方法的检测结果, 其中蓝色虚线框是第1次检测结果, 红色实线框为二次检测的结果, 图9 (b)显示了对于该图像基于区域生长法的太阳活动区检测结果图. 由于图9 (a)中左上角区域的精确检测定位结果日面经度延伸大于20°, 因此对该区域进行二次检测. 图10 (a)是该区域的二次检测聚类决策图, 在该图中, 满足二次聚类判据的特征点共有两个, 分别用编号1、2加以标注; 图10(b)是根据决策图的决策结果对上述区域进行二次检测,得到的两个活动区分别用编号1、2加以标注.这样一来, 一次检测中多个邻近活动区被误检为一个活动区的问题得到了解决.

图9 (a)本文算法检测结果; (b)区域生长法检测结果.Fig.9 (a) The results of the proposed algorithm; (b) the results of the region growing algorithm.
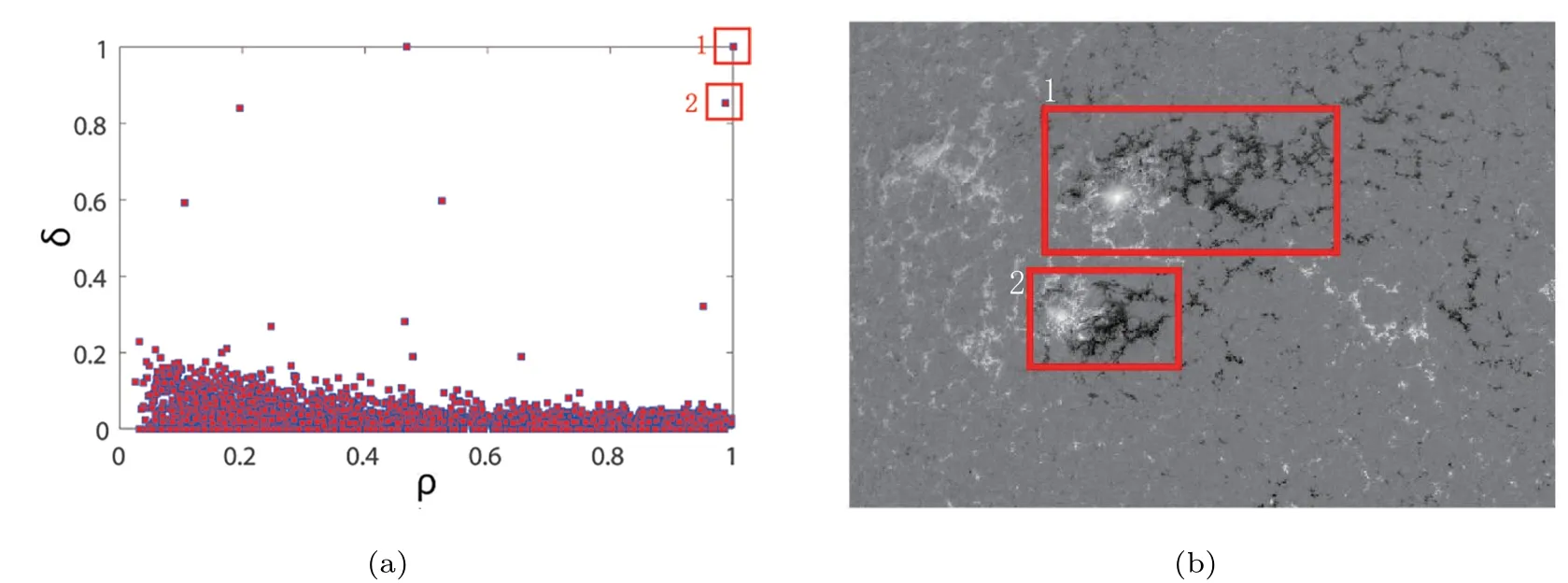
图10 针对误检的太阳活动区二次检测结果. (a)密度峰值聚类决策图; (b)精确定位区域的二次检测结果.Fig.10 The second detection results of erroneous solar activity regions. (a) Decision graph of second detection; (b) the second detection results of accurate positioning.
通过两种方法的对比, 本文的检测算法具有以下4个优势: (1)自动化程度高, 相比区域生长法,本文算法不需要提前选取种子点, 所有特征点的提取全部是自动进行的; (2)区域生长法可能将相邻的活动区检测为一个活动区, 比如图9 (a)中编号为1和2的两块活动区, 在图9 (b)中区域生长法误检测成了一个活动区(编号1); (3)对于较大型活动区的延伸区域以及双极相隔较远的太阳活动区, 区域生长法可能会导致一个活动区被误检为两个, 比如图9 (a)中编号3和4的两块活动区, 在图9(b)中区域生长法分别将其误检成了编号2和3以及编号4和5两个活动区; (4)区域生长法的活动区候选区域通过强度阈值确定, 因此会对强磁性但非活动区的区域产生误检[10].
经过上述结果对比分析, 本文算法可以有效地自动检测全日面上的太阳活动区. 而传统方法中存在的由于活动区双极相距较远而导致被误检为多个活动区, 或者多个相距较近的活动区被误检测为一个活动区等问题[10], 本文算法也能较好地解决.
4 总结与展望
本文提出了一种基于SIFT特征检测与密度峰值聚类相结合的太阳活动区自动检测算法. 该算法分为两步: 首先, 采用SIFT算法提取全日面图像的特征点; 其次, 基于密度峰值聚类算法对特征点进行聚类, 初步确定活动区, 然后采用自动阈值分割对活动区精确定位. 对不同复杂程度的全日面磁场图像进行了活动区检测, 结果表明该算法可以较为准确地提取出太阳活动区, 且鲁棒性较强, 自动化程度较高. 需要指出的是, 该算法也有不足之处, 对太阳边缘的活动区进行检测时的准确率会下降, 因此如何提高边缘区域的活动区检测准确度将是我们下一步研究的方向.

