考虑LS+AR模型基础数据量的极移预报研究*

徐海龙 乔书波 王穆阳

(1 信息工程大学地理空间信息学院 郑州 450001)

(2 31121部队 南京 210018)

1 引言

地球定向参数(Earth Orientation Parameter,EOP)是实现天球参考框架和地球参考框架转换的必要参数, 对于高精度导航定位、卫星精密定轨和深空探测等方面有着重要意义[1]. 地球定向参数的观测模式、数据处理和解算较为复杂, 导致EOP的解算结果通常具有几小时至数天的延迟, 用户不能得到实时EOP数据, 因此, EOP的短期至中长期预报数据在卫星自主导航和天文动力学研究中有重要的应用[2]. 地球定向参数由极移(Polar Motion,PM)、日长变化、岁差和章动组成, 极移的两个分量又可以分别用PMX和PMY表示. EOP中岁差和章动模型IAU2000/IAU2006拟合精度较高, 可以实现长期高精度预测[3]. 所以, 当前对地球定向参数的预报研究主要是极移的两个分量和日长变化,这两者又被统称为地球自转参数(Earth Rotation Parameter, ERP).

国内外学者相继提出了多种预报方法, 如最小二乘(Least Square, LS)外推和自回归(AutoRegressive, AR)组合模型[4–5]、LS外推和神经网络(Artificial Neural Network, ANN)组合模型[6–8]、灰色模型[9]、模糊推理系统[10]、自协方差模型等以及这些模型的组合及改正算法[11–12]. 为了比较验证当前各种预报方法的精度和稳定性, 进一步提高地球定向参数的预报精度, 维也纳理工大学依托国际地球自转与参考系服务(International Earth Rotation and Reference Systems Service, IERS)在2005年到2008年组织了地球定向参数预报比较活动(Earth Orientation Parameter Prediction Comparison Campaign, EOP PCC). 此次活动在全球范围内有8个国家共12个相关领域顶尖专家或小组参与, 涉及20种预报方法, 最终结论表明对于极移序列预报精度最高的为LS+AR模型[3].

基于LS+AR模型, 相关学者在模型改进和数据选取方面展开了广泛研究, 进一步提高了模型预测精度.模型改进方面,姚宜斌等[13]通过对LS+AR模型短期预报残差的相关性分析, 提出了利用预报残差和调节矩阵修正结果的新模型; 加松等[14]利用Kalman滤波对AR模型修正、利用最小均方误差自适应滤波对LS拟合外推项修正, 两种修正模型的预报精度均较LS+AR模型有较大提升. 张昊等[15]、Sun等[16]和孙张振[17]针对极移近期数据与未来走势相关性更强的特点, 并结合数据解算精度, 通过不同方法设计了LS拟合时的权矩阵,有效提高了极移预报精度. 数据选取方面, 随着EOP的测定精度不断提高和数据长度的增加, 相关学者也注意到不同的基础序列长度影响极移预报结果的精度. 姚宜斌等[13]在研究附加误差修正的LS+AR新模型时, 选用了6、9、12和15 yr 4个不同长度的极移序列进行预报, 结果显示在进行10 d和30 d预报时, 采用6 yr的极移序列精度优于其他长度序列预报结果; 严凤等[18]通过实验对比发现,对于1–10 d的ERP超短期预报, 基础序列越长反而精度越差, 6 yr是超短期预报的最优基础序列长度;Xu等[19]采用LS+AR模型进行地球自转参数预报时, 通过计算不同长度输入序列和对应预报跨度关系, 证明了对于预报不同跨度时需要输入不同的最优基础序列长度.

上述针对LS+AR模型的研究均是将该组合模型看作一个整体, 数据选取时只是变化不同长度的基础序列, 将预报结果对比后确定LS+AR模型的单一最优基础长度. 然而这种数据选取方法并不理想, 如果数据量太小则LS模型不能很好地提取周期信息, 如果数据量太大又容易导致输入AR模型的残差数据冗余, 使模型过拟合造成模型偏差较大从而影响精度. Wu等[20]对输入AR模型的数据量进行了讨论, 结果表明采用不同大小的LS残差数据量对AR模型的预报精度影响较大, 但文献中LS基础序列采用的是固定10 yr长度进行实验, 并不能代表LS+AR模型整体输入数据序列的最佳长度. 本文在实验中考虑LS模型和AR模型各自拟合需求的不同, 分别计算确定用于极移预报的最优组合数据长度, 将最终预报结果同只确定一个基础序列长度的预报结果对比, 并在最后给出结果分析.

2 预报模型与原理

使用LS+AR模型预报时, 首先用LS模型对极移序列的线性趋势项和主要周期项进行拟合并外推预测, 然后使用AR模型对LS拟合残差序列进行建模预报, 最后将LS外推值和AR模型预报值相加即为最终预报结果.

2.1 LS模型

时间序列中经常出现线性趋势项和谐波振荡周期项, 极移序列中同样存在趋势项和周期项. 该确定性部分可以利用下式的最小二乘模型进行拟合外推, 并得到LS拟合残差项.

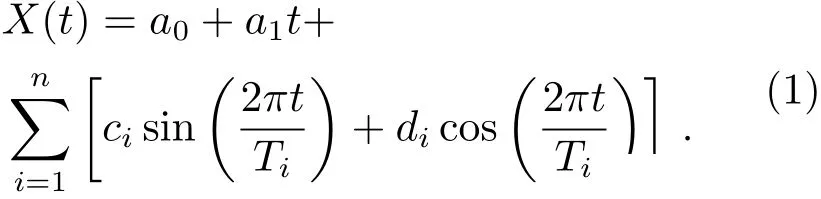
式中,t为时间,X(t)表示t时刻的极移数值,a0和a1表示序列线性趋势项参数,i为拟合时第i个周期项,ci和di表示序列的各周期项参数,Ti表示周期时长,n表示周期项个数. (1)式中前两项为线性部分,可对极移序列的线性趋势项拟合, 后一项由三角函数构成, 可对极移序列的周年、半周年和钱德勒项等周期项进行拟合.

2.2 AR模型

对极移序列确定性部分进行建模和预报后, 剩余残差项采用自回归AR模型拟合预报. AR模型是一种根据时间序列变量自身过去的规律来建立的预报模型[11], 其数学模型为:

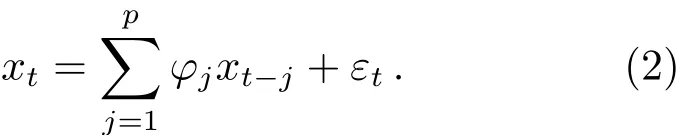
式中,xt为残差序列,φj为AR模型的第j个参数,εt为拟合后剩余噪声序列,p为模型阶数. (2)式又可称为p阶自回归模型, 简称为AR(p).

使用AR模型进行预报关键在于模型阶数的确定, 常用的定阶准则有最小信息量准则(Akaike Information Criterion, AIC)、最终预报误差准则(Final Prediction Error, FPE)和矩阵奇异值分解(Singular Value Decomposition, SVD)等. 本文在实验中使用AIC准则进行模型定阶. AIC准则的思想是通过两个方面去衡量拟合模型的优劣[21]: 综合考虑拟合程度的似然函数值和拟合模型中未知参数个数. 通常来说, 似然函数值越大就代表该模型拟合效果越好. 模型未知参数个数越多代表模型灵活度较高、模型拟合准确度较高. 而从另一个方面看, 模型参数越多也代表参数估计难度加大, 容易导致模型精度变差. 所以如何发现未知参数和拟合精度之间的最优配置, 对最优模型至关重要.AIC准则即是拟合精度和未知参数的加权函数, 使AIC函数值达到最小的模型也称为最优模型.

通过AIC准则确定AR模型阶次p, 便可进一步利用时间序列估计模型中未知参数. 最经典的方法是利用最小二乘估计对AR(p)模型参数求解[21], 首先对于(2)式中的待求参数φ1,φ2,···,φp可以用表示, 即:

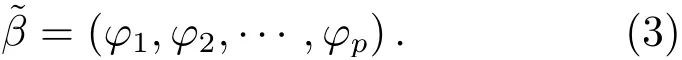
则AR(p)模型拟合值Ft()为:

此时, 残差项如(5)式所示. 最小二乘原理指出, 使残差平方和Qt(β)达到最小的参数值即为参数~β的估计值, 可如下计算:

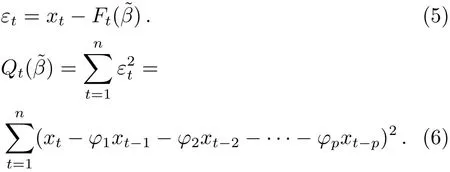
该解算策略充分利用了时间序列的信息, 因此最小二乘估计的精度很高. 利用此过程得到AR(p)模型参数, 最后根据下列方程进行序列多步预报:

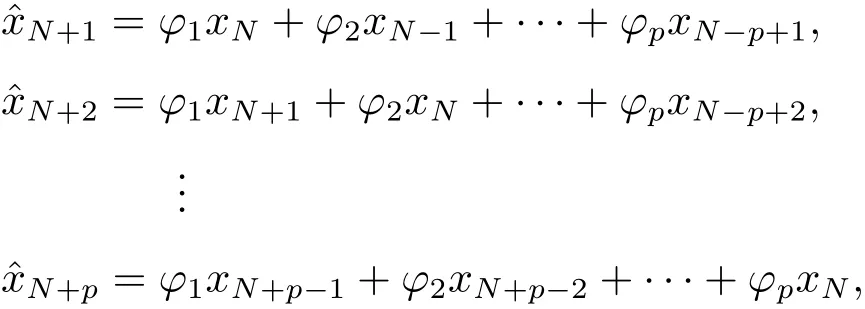
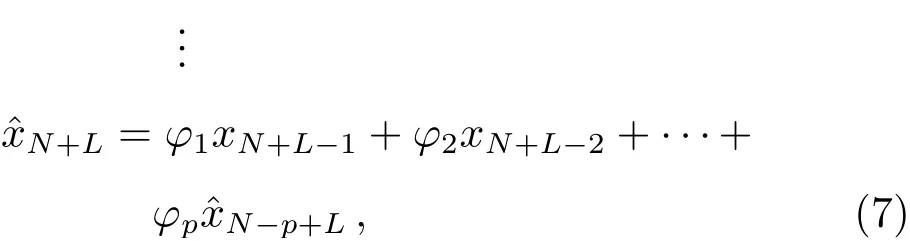
其中,N表示模型输入基础序列长度,xN为第N天的残差序列值,L为AR模型的预报跨度,, ···,为AR模型预报结果.

3 实验分析

3.1 精度评价标准

本文采用EOP PCC推荐的平均绝对误差(Mean Absolute Error, MAE)作为最终精度评价标准, 并增加绝对误差(Absolute Error, AE)来进一步验证对比预报稳定性, 其公式分别如下:

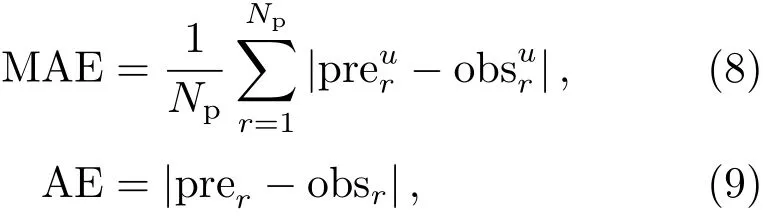
式中, prer和obsr分别为极移PMX和PMY序列第r天的预报值和真实值,u为预报跨度,Np为预报天数, MAE表示平均绝对误差, AE表示预报值与真实值绝对差值.

3.2 实验及结果

极移预报的基础序列大多来自IERS发布的EOP C04序列, 该序列为1962年以来间隔1 d的地球定向参数. 本文选用当前最新的EOP 14C04序列中的极移数据进行实验(https://hpiers.obspm.fr/iers/eop/eopc04). 预报起始时间为2018年1月第1周, 每周预报1期, 每期预报360 d, 至2019年12月底结束预报共计104期. 实验时的基础数据分别采用原始方式的单一数据长度和本文的组合数据方式.单一数据分别选择3、6、9、12、15、18、21和24 yr作为实验基础序列长度, 利用LS+AR模型进行预报, 以便得出模型最优单一基础序列长度. 本文组合数据同样分别选择3、6、9、12、15、18、21和24 yr作为实验预报序列长度, 首先利用LS模型进行拟合外推并得到残差序列, 然后重新选择1/5、2/5、3/5、4/5长度的残差序列输入AR模型进行预报, 两者预报值相加即为最终预报值, 即可对比选出适合模型的最优组合基础序列长度.

图1为极移PMX和PMY分量使用单一基础序列长度时的实验结果. 结果显示除1–10 d的超短期预报精度比较接近外, 随着预报跨度的增加, 预报时输入基础数据长度不同, 对应预报精度也不同.对于PMX和PMY分量, 最优单一基础数据长度均为6 yr, 这一结论与姚宜斌等[13]、严凤等[18]的工作一致. 分析发现, 这主要是因为6 yr正好是极移序列约1.2 yr的钱德勒项周期和周年项周期的最小公倍数, 一定程度上体现了极移的周期特征; 另一方面, AR模型作为LS+AR模型的一部分, 其处理的是LS模型的拟合残差序列, 如果数据量太少, 可能引起AR模型拟合时参数解算方差过大; 而过多的数据可能造成AR模型过拟合, 导致模型偏差较大,对最终预报结果产生影响. LS模型和AR模型之间这种微妙的制约关系, 使得6 yr成为适合LS+AR模型的单一基础序列长度. 但这种简单使用6 yr长度的LS+AR模型实验, 并不能代表模型的最适合数据量, 所以仍需要进行组合数据实验验证才能得出分别适用于LS模型和AR模型的数据长度.

图2和图3分别为极移PMX和PMY分量预报结果. 当实验选择不同的基础数据长度时, 对应的AR模型所输入的数据也不同, 实验中各分量分别产生32种结果, 其中当LS拟合基础数据长度为21 yr, AR拟合数据量为1/5残差总长时, PMX和PMY分量预报结果精度均最高. 进一步分析可以发现, 当基础数据长度为21 yr时, 预报精度随着AR模型数据量比例增大而减小, 这可能是因为采用过长或过久的残差序列造成AR模型存在过拟合, 导致模型偏差较大而影响预报精度.

图2 PMX分量不同组合数据预报精度. 其中图(a)、(b)、(c)和(d)分别表示AR模型输入数据量分别为LS拟合残差序列长度的1/5、2/5、3/5和4/5.Fig.2 The prediction accuracies of combined data of PMX. In the figure, panels (a), (b), (c) and (d) indicate that the input data amount of AR model is 1/5, 2/5, 3/5 and 4/5 length of the residual sequence of LS fitting, respectively.

图3 PMY分量不同组合数据预报精度. 其中图(a)、(b)、(c)和(d)分别表示AR模型输入数据量分别为LS拟合残差序列长度的1/5、2/5、3/5和4/5.Fig.3 The prediction accuracies of combined data of PMY. In the figure, panels (a), (b), (c) and (d) indicate that the input data amount of AR model is 1/5, 2/5, 3/5 and 4/5 length of the residual sequence of LS fitting, respectively.

将组合数据模式实验中的预报最优结果与图1中最优单一数据为6 yr时极移预报结果对比. 统计结果如表1所示, 表中“6”即代表单一基础数据长度为6 yr, “21+1/5”代表组合长度为LS选择21 yr、AR模型选择1/5残差总长的最优组合数据. 表1所示为单一数据和组合数据分别进行极移两个分量预报时的MAE精度对比.对于PMX分量,组合数据结果在1–360 d的预报跨度上比单一数据预报结果具有更高的精度, 从50 d开始, 组合数据相对单一数据的预报精度提升百分比达到14%, 最大可以达到28%, 第100 d后稳定在20%以上. 对于PMY分量,在预报初期组合数据预报结果精度略低于单一数据, 但两者相差不大. 随着预报跨度的增加, 至第30 d开始精度逐渐优于单一数据结果, 精度提高比例最高时也可以达到23%. 结果表明, 对于1–360 d跨度的极移序列预报, 本文采用的组合数据预报相比单一数据预报精度提高较大.

表1 两种数据方案预报精度统计(MAE: mas)Table 1 Statistic of the two kinds of data accuracies (MAE: mas)

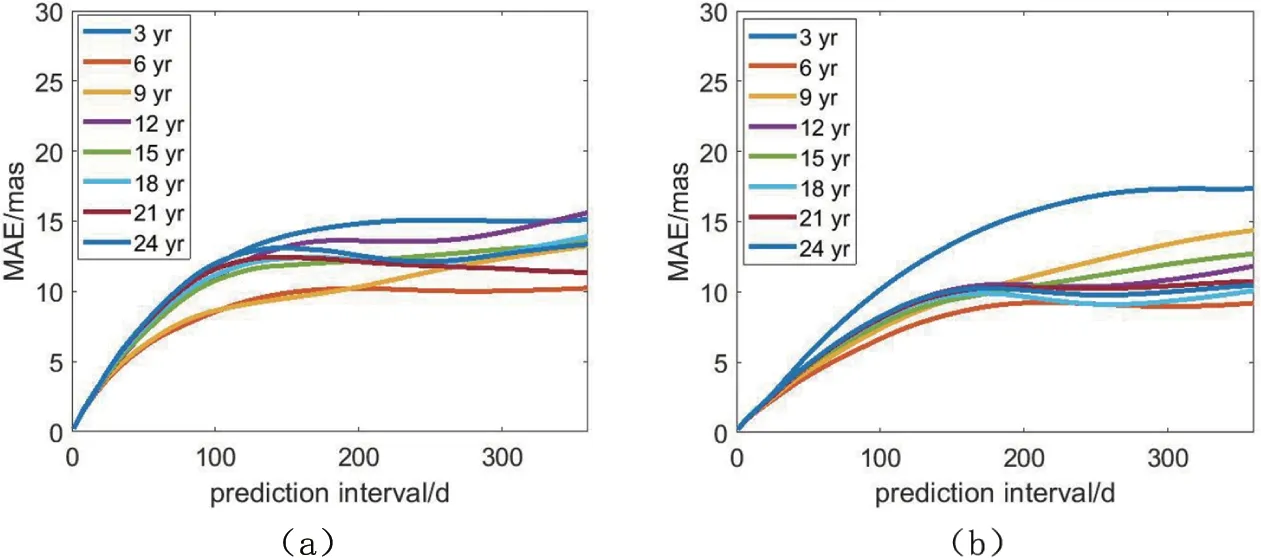
图1 PMX分量(a)和PMY分量(b)单一数据预报精度Fig.1 The prediction accuracies of single data of PMX (a) and PMY (b)

从预报跨度来看, 短期1–30 d的预报跨度内提升效果不佳, 甚至PMY分量的组合数据预报结果误差略有增加, 但随着预报时长的增加, 组合数据预报优势逐渐显现, 较单一数据结果精度提升效果明显. 这是因为在短期30 d内时, 极移整体变化幅度不是很大, 数据量的改变对预报影响还不是特别明显. 随着预报跨度的增加, 当进行至30–200 d左右的预报时, 组合数据预报精度稳步提升, 在这一阶段, 组合数据长度的优势使得LS模型和AR模型各自的预报精度都在提高, 所以预报精度提高比例也在上升. 而当预报跨度增加到200–360 d, 预报精度提高比例趋于稳定. 这可能是因为随着预报跨度的增加, AR模型残差部分预报值所发挥的作用逐渐减小, 而21 yr的LS拟合基础序列, 包含信息更加丰富, 更适合中长期预报, 此时预报结果主要由趋势项和周期项预报值主导所致.

为进一步研究证明组合数据结构有利于极移预报精度的提高, 分别计算预报时段内每期绝对误差AE, 统计如图4和图5所示. 通过分析104期预报绝对误差可以看出, 组合数据预报结果的绝对误差相比单一数据也有了明显改善, 而且当预报跨度较大和预报误差较大时改善效果更加明显. 这是由分别计算决定LS+AR模型数据量的优势决定的. 使用21 yr的长期数据进行LS拟合, 可以充分提取序列中的周期信息, 而AR模型使用少部分的残差序列即避免了冗长数据对AR模型参数求解的影响,也很好地利用了临近数据的相关性, 这也进一步证明了本文数据选取方法在理论上的合理性.

图4 PMX分量单一数据(a)和组合数据(b)绝对误差统计Fig.4 Statistic of absolute error of single data (a) and combined data (b) of PMX

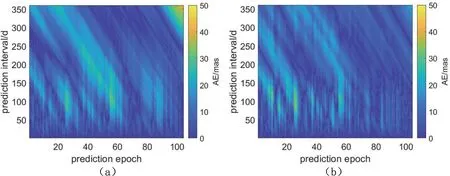
图5 PMY分量单一数据(a)和组合数据(b)绝对误差统计Fig.5 Statistic of absolute error of single data (a) and combined data (b) of PMY

4 结语

本文通过对LS+AR模型分别采取单一数据量和组合数据量的预报结果统计分析, 发现数据量的不同对于极移预报结果影响较大. 通过实验分析,显示单一数据序列在使用6 yr长度作为极移最优数据时预报结果最好, 组合数据预报在使用21 yr长度的LS拟合序列和1/5残差长度的AR拟合序列时预报精度最高. 对这两种不同数据选取方式的预报结果进行对比, 结果表明, 在进行1–30 d的极移短期预报时, 改变输入数据的选取方式对预报精度影响较小, 但在进行30 d以上中长期预报时, 组合数据预报精度相较于单一数据预报结果具有较大的提升, 其中PMX分量精度提升最高为28%, PMY分量最高为23%. 建议在极移分量的预报中, 可以采用组合数据预报, 以提高当前极移的预报精度. 需要注意的是, 本文实验只是探索验证了组合数据的可行性, 所得出结果也只是数据选取的一个大概合适范围, 但给出的结果仍可以证明组合数据预报结果在360 d的预报跨度内精度更高.

致谢感谢参与本文评审的各位专家对文章提出的宝贵建议, 使得文章的质量有了显著的提高. 感谢IERS提供地球定向参数数据.