射频干扰检测的SumThreshold算法*

李 慧 丁雨君 李乡儒 张金区

(1 华南师范大学计算机学院 广州 510631)

(2 华南师范大学数学科学学院 广州 510631)

1 引言

射电天文学是现代天文学的重要分支[1–2]. 由于仪器的高灵敏度和电子类产品的普及, 射电天文数据会受到人类生产、生活以及非观测目标的宇宙辐射源产生的射电信号的影响, 此类影响称之为射频干扰(Radio Frequency Interference, RFI)[3–5].宇宙辐射源, 如太阳, 可能会干扰观测. 这类干扰由于位置和强度已知, 易于回避或纠正. 但人为活动产生的干扰, 通常不可预测且不稳定、强度未知、难以控制[6]. 常见的射频干扰源包括电视信号、调频无线电传输、全球定位系统、手机和飞机导航通讯等[7]. 不同射频干扰源的频率和时间特性有差异, 导致整个RFI检测问题很复杂. 射频干扰检测成为射电观测数据处理中遇到的重要挑战之一.

因此, 该问题备受关注, 而且研究者给出了一系列RFI检测方法. 从原理上来说, RFI检测方法大致可分为成分分解法、阈值分析法和机器学习法等. 成分分解法的基本思想是从数据中自动发现RFI在时间或频率方面展现出来的规律性, 据此实现对RFI与非RFI数据成分的分离. 这类方法适用于RFI在时间或频率上表现出重复模式的情况, 但是不能处理各种不规则信号[1]. 例如, 奇异值分解法(Singular Value Decomposition,SVD)[8]和主成分分析法(Principle Component Analysis, PCA)[9–10]都是典型的成分分解类RFI检测方法.

随着机器学习的迅猛发展和广泛应用, 聚类分析法、卷积神经网络法等机器学习方法在RFI检测[11–13]中的应用渐受关注. 机器学习算法可从海量数据中学习数据的知识表示和数据成分之间的复杂关系,进而完成模式的发现或识别,并在RFI检测中初步展示出了不错的应用潜力. 但是机器学习模型训练耗时, 模型正确性验证复杂, 而且样本数据和特征的选择直接影响其分类精度, 特别是有标注样本数据不足时难以得到高精度的训练模型.

阈值分析法因其实现简单、检测结果精度较高而被广泛应用. 它的理论依据是射电天文望远镜所接收到的来自地球辐射源产生的RFI信号的强度往往大于来自太空的信号强度. 因此, 当一个信号强度值超过某个阈值时, 阈值分析法可将它标记为RFI. 代表性阈值分析法有CUSUM (cumulative sum)法[14]、Simple Thresholding法[15]和Combinatorial Thresholding法[16]等. CUSUM算法通过估算累积样本的方差或平均值得到阈值, 高于阈值的数据被标记为RFI. 此方法简单、快速, 但是无法检测到RFI出现的准确起始时间, 只能用于估计其粗略范围. 因此, CUSUM适合于RFI的预检, 即首先用CUSUM发现存在RFI的粗略位置, 然后用其他更准确但相对耗时的方法精确标记[16]. Simple Thresholding方法在检测某行(列)的观测数据时, 使用该行(列)的中位数作为阈值.该方法运行速度快, 但在检测瞬时射频干扰时,仅可以检测到干扰的峰值, 通常会忽略上升过程中部分强度弱的RFI样本点. 然而, RFI干扰往往会影响相邻位置的多个样本. 因此, Simple Thresholding方法易造成漏检. 为此, Combinatorial Thresholding算法通过采用滑动窗口与多次迭代的机制进行检测, 当样本组合的值超过阈值时, 将该样本组合标记为RFI. Combinatorial Thresholding算法解决了Simple Thresholding算法瞬时射频干扰RFI漏检的问题, 但存在RFI过检测倾向[15]. 因此, 学者们提出了改进算法VarThreshold和SumThreshold. 当检测窗口内所有样本的读数均大于阈值时, VarThreshold算法将窗口内的样本标记为RFI. 而SumThreshold算法则仅关注窗口内尚未被检测为RFI的像素: 如果这些像素的均值大于给定阈值, 则将它们标记为RFI. RFI强度可变、形态多样以及不可预测的性质使得检测具有挑战性, 构建稳健的RFI检测方法至关重要[17]. 研究表明, SumThreshold方法在RFI检测中具有较高的精度[16], 已经广泛地应用于射电天文数据处理中[18–21], 成为RFI检测的典型算法. 因此, 本文从原理、性能、优化等方面对SumThreshold算法进行深入探讨, 以期促进Sum-Threshold算法的研究和应用.

2 SumThreshold算法描述

在射电天文学中, 射频干扰可分为3类: 脉冲干扰、长窄带干扰和复合干扰[15]. 脉冲干扰是指在短时间内出现的较宽频带干扰. 长窄带干扰中干扰是出现在某个小的频率子带内的一个相对恒定的流. 复合干扰是前两种干扰的组合. 由此可知, RFI干扰在时间或频率上会影响多个位置连续的像素.传统阈值分析法是通过对单一数据值与某个指定的阈值做比较实现RFI检测. 但是, 这类基于单个像素比较的阈值类方法也存在一定的局限性: 会引起个别像素的RFI假阳性或假阴性. 对此, 一种解决思路是将像素邻近性因素纳入考虑之中.

为了充分利用RFI数据间的位置邻近性, Sum-Threshold算法构造了滑动窗口和阈值集合. 当检测窗口内数据的均值高于阈值时, 窗口内数据被标记为RFI. 通过窗口的滑动和迭代, 实现对整个观测数据的RFI检测. SumThreshold的算法流程如图1所示.

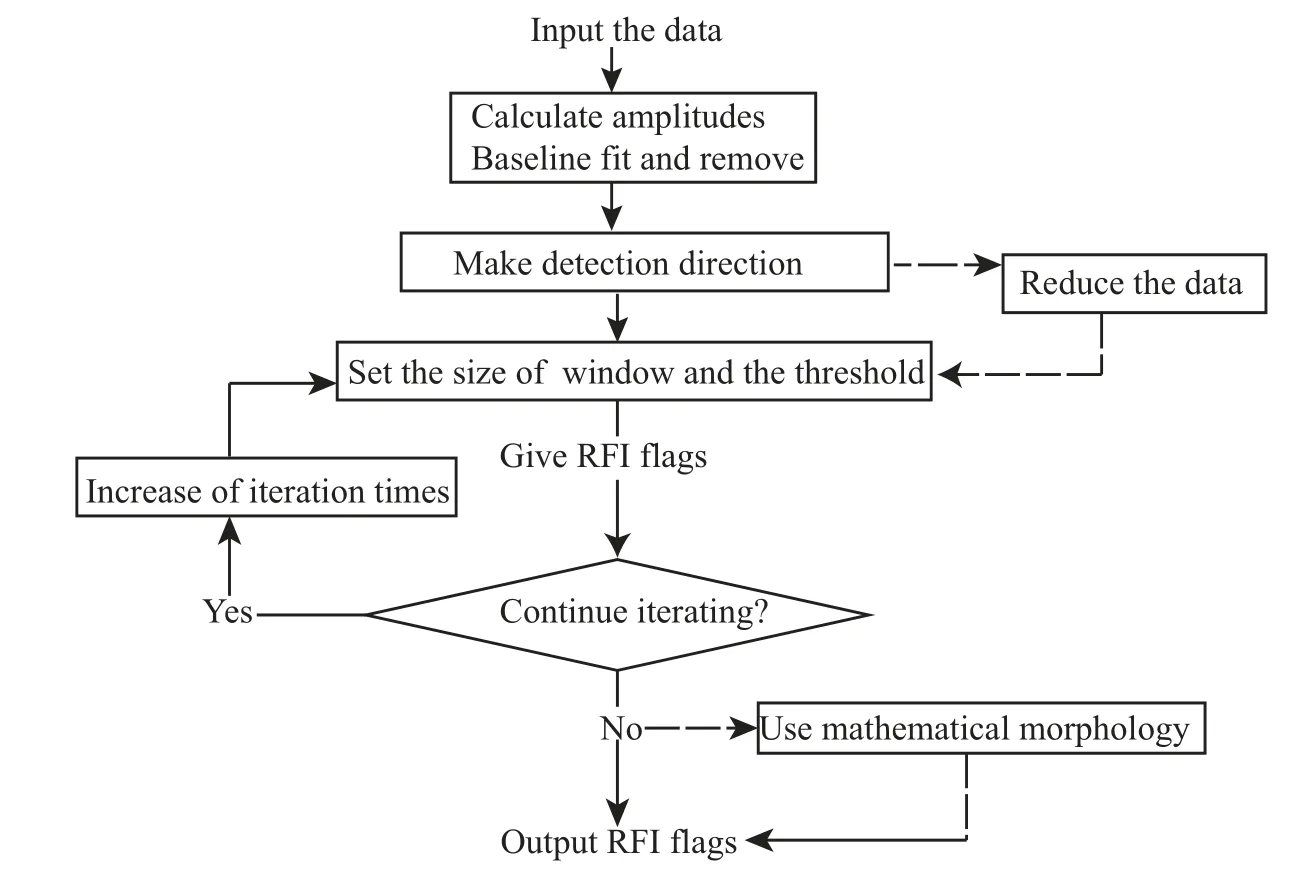
图1 SumThreshold的算法流程图Fig.1 The flow chart of SumThreshold method

2.1 基线矫正

阈值法进行RFI检测的基本前提是: 如果数据没有受到RFI干扰且未叠加射电天文信号, 则相应的读数基本恒定[22], 并将其简称为背景响应恒定假设. 理想情况下, 基线在频域和时域中保持恒定. 但是, 几乎所有的射电天文数据受到系统漂移、大气效应、地面辐射等因素的影响, 由此导致背景恒定假设一般不成立. 这种背景不恒定性在有些文献中称为基线变化. 例如, 图2展示了一幅500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope,FAST)的时间-频率观测图像[23], 观测时间为0.05 s, 频率范围是1000–1500 MHz; 在该观测中基线变化导致低频带像素读数较低, 且像素读数随着频率的增大而整体上增大. 这种基线变化致使非RFI数据读数取值区间范围增大, 无法直接通过某个固定阈值实现RFI检测.为此, 在运用SumThreshold算法检测RFI之前, 需进行基线拟合和剔除, 尽量减少背景不恒定性造成的影响.

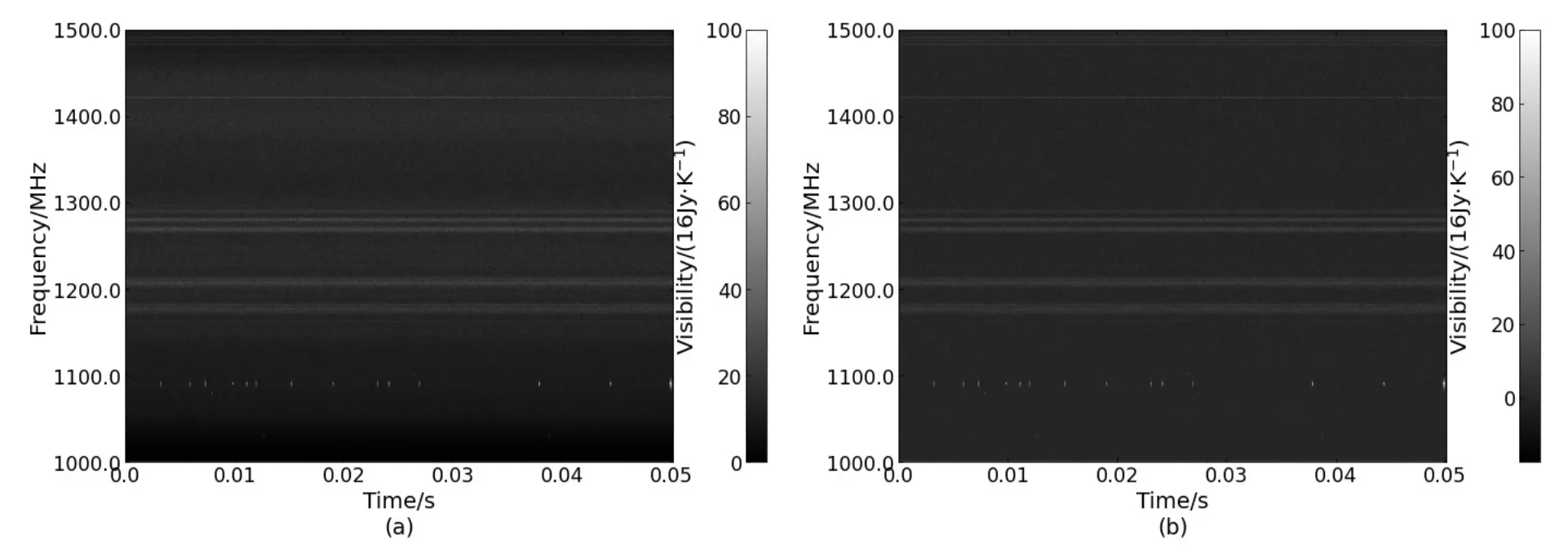
图2 基线对阈值类方法的影响. 这是FAST的一个时间-频率观测图像, 观测时间为0.05 s, 频率范围是1000–1500 MHz[23]. (a)原始观测数据;(b)去除基线效应后的结果. 原始观测数据中不同频带像素读数浮动范围变化非常大, 对RFI检测中的阈值设定造成困扰.Fig.2 The influence of baseline on the threshold method. This is a time-frequency image observed using FAST for 0.05 s in the frequency range from 1000 to 1500 MHz[23]. (a) An original time-frequency image; (b) the result after baseline removal. The range of pixel intensity is very broad in different frequency bands of the original observation, so that it is hard to set an appropriate threshold for RFI detection.

文献[23]运用非对称加权惩罚最小二乘法(Asymmetrically reweighted Penalized Least Squares, ArPLS)进行基线拟合和剔除. 与传统的二维低阶多项式法[16]相比, 此方法更加高效、准确和稳健. 基线剔除修正了原图数据的背景不一致性, 原始图像中对比度低的区域变得易于检测RFI (图2).

2.2 RFI检测方向指定

对于时间-频率观测数据, 基于SumThreshold算法的RFI检测有3个实施策略: 基于时间维度的RFI检测、基于频率维度的RFI检测以及基于时间和频率的双向检测. 基于时间和频率的双向检测, 首先沿着时间维度检测RFI, 然后基于第1次检测结果,在频率方向继续进行RFI检测,这种检测策略简称为时间-频率双向检测, 反之则称为频率-时间双向检测. 为了比较3种实施策略的效果差异, 本文基于FAST观测数据[23]进行实验. 图3的FAST观测数据中由于存在取值较大的RFI, 导致图像细节不明显. SumThreshold算法单一方向RFI检测结果对比见图4. 图4 (a)、(b)为沿时间维度或频率维度的单一方向RFI检测结果. 图4 (c)、(d)展示的是仅一方向检测发现的RFI. 实验结果表明, 两种单一方向的检测策略实验结果存在差异. 但是, 强干扰在两种检测策略里均被正确检测, 而存在差异的是较弱的RFI.

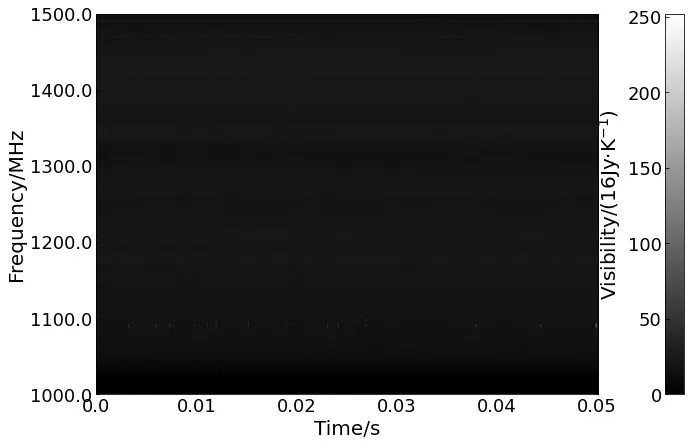
图3 FAST观测数据. 观测时间为0.05 s, 频率范围是1000–1500 MHz. 由于存在取值较大的RFI, 导致图像细节不明显.该数据来源于FAST观测[23].Fig.3 A time-frequency image of FAST observation for 0.05 s in the frequency range from 1000 to 1500 MHz. There are some RFI with extremely large values. Therefore,visibility of the image details is poor. The experimental data are of a FAST observation[23].

因此, 在实际应用中一般采用基于时间和频率的双向检测策略. 图5 (a)是先沿着时间方向再沿着频率方向的RFI检测结果, 图5 (b)是先沿着频率方向再沿着时间方向的RFI检测结果. 与单一方向检测结果(图4)相比, 双向RFI检测能够更全面地发现RFI. 图6为基于不同双向检测策略的SumThreshold算法效果对比, 结果表明频率和时间检测方向的先后顺序不同时, RFI检测结果有一定差异.基于双向检测和单向检测的SumThreshold算法检测结果比较如图7所示.将单一时间维度RFI检测结果和频率维度RFI检测结果合并, 与双向RFI检测结果对比发现, 前者检测RFI数量大于后者. 这主要是因为, 基于双向标记策略的SumThreshold算法在标记过程中, 当第1个方向完成检测时, 会对下一个方向的检测产生影响, 即部分样本点在上一个方向的检测中已经被标记, 从而导致在进行下一方向检测时, 未标记样本点的平均值减小. 在阈值集合不变的情况下, 第2方向检测的RFI数量减少. 因此, 可以在第2方向检测时, 根据数据的分布特征,调整阈值参数χ1, 进而得到更优的阈值集合(阈值集合的详细讨论, 见本文2.3节).

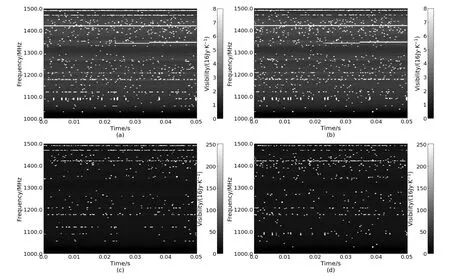
图4 SumThreshold (ST)算法的不同实施策略效果比较. (a) ST算法沿时间维度的RFI检测结果; (b) ST算法沿频率维度的RFI检测结果;(c)在图(a)中被检测到但未在图(b)中检测到的RFI; (d)在图(b)中被检测到但未在图(a)中检测到的RFI. 图中白色点表示RFI数据. 由于强干扰被两种策略均正确检测, 所以在图(c)和(d)中均未标记, 且它们比图(a)和图(b)整体上显得暗一些. 该数据来源于FAST观测[23].Fig.4 The detection results of SumThreshold with different implementation schemes. (a) The results detected along time direction; (b) the results detected along frequency direction; (c) the RFI detected only along time direction, but not frequency direction; (d) the RFI detected only along frequency direction, but not time direction. The RFI data are presented in white.Strong RFI are successfully detected by both strategies. Therefore, these strong RFI are not showed in panels (c) and (d), and panels (c) and (d) are darker than panels (a) and (b). The experimental data are of a FAST observation[23].

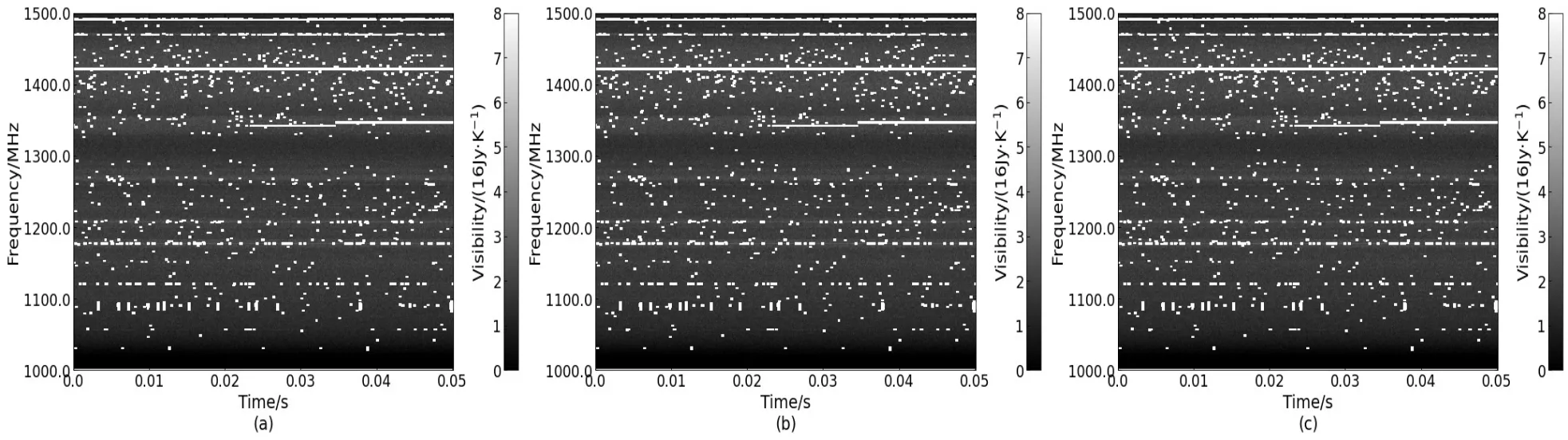
图5 双向SumThreshold算法的RFI检测结果. (a)先沿着时间方向再沿着频率方向的RFI检测结果(简称为时间-频率双向检测); (b)先沿着频率方向再沿着时间方向的RFI检测结果(简称为频率-时间双向检测); (c)将图4 (a)和(b)单一方向检测结果合并后的RFI标记结果. 该数据来源于FAST观测[23].Fig.5 The RFI detection results based on bidirection detection. (a) The RFI detection results detected firstly along time direction and then frequency direction (time-frequency bidirection detection); (b) the RFI detection results firstly along frequency direction and then time direction (frequency-time bidirection detection); (c) the RFI detection result from panels 4(a) and (b). The experimental data are of a FAST observation[23].

图6 基于不同双向检测策略的SumThreshold算法效果对比. (a)被时间-频率双向方式检测到但未被频率-时间双向检测方式发现的RFI; (b)被频率-时间双向检测方式发现但未被时间-频率双向检测方式发现的RFI. 由于强干扰被两种双向策略均正确检测, 所以它们在这个实验中均未标记, 且该图比图5整体上暗一些. 该数据来源于FAST观测[23].Fig.6 Detection result comparison of the SumThreshold with different bidirection detection schemes. (a) The RFI detected by SumThreshold with time-frequency scheme; (b) the RFI detected by SumThreshold with frequency-time scheme. Strong RFI are successfully detected by both strategies. Therefore, the strong RFI are not showed in Fig.5 but exist in (a) and (b) of Fig.6.The existences of the strong RFI make the panels (a) and (b) of Fig.6 darker than Fig.5. The experimental data are of a FAST observation[23].

2.3 使用SumThreshold算法对RFI进行检测

使用SumThreshold算法对RFI做检测需要进行多次迭代. 每次迭代, 使用某个指定大小的窗口沿着时间或频率方向进行移动, 并对窗口内的像素求平均值, 据此进行阈值检测. 检测窗口的尺寸随着迭代次数的增加而增大. 例如, 当时频数据有N个观测频带时, 跨频带方向移动检测的情况下最多可迭代N次. 实际应用中, 一般不需要进行最大次数的迭代即可取得良好结果. 文献[23]中根据FAST数据的特点, 经验性地将迭代次数设置为11.

2.3.1 RFI数据标记准则

在SumThreshold算法每次迭代中, 给定迭代窗口的大小和相应的检测阈值. 根据算法原理可知, 之前迭代中已被标记RFI的像素在新一轮迭代中将被替换为当前的检测阈值. 这样的数据重置,可避免一些RFI像素造成周围非RFI像素被错误检测为RFI(假阳性). 因此, 对于每个检测窗口, 实际上是计算当前窗口内尚未被检测为RFI像素的均值, 据此判断这些像素是否为RFI成分[16,21,23]. 基于SumThreshold的RFI检测原理可形式化表达为:

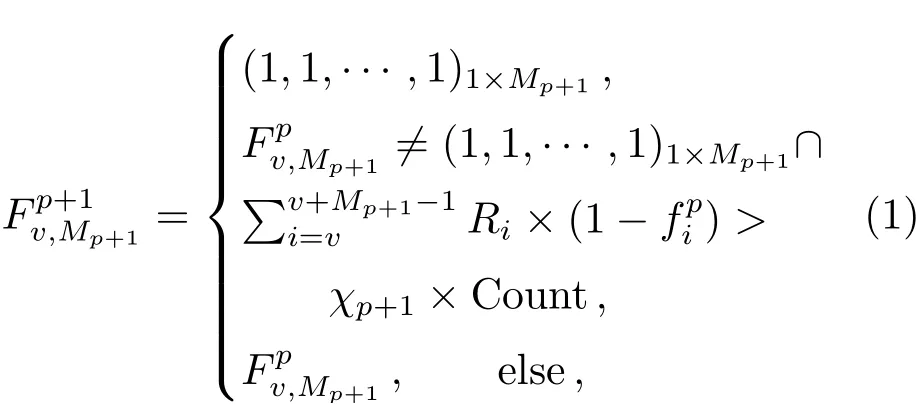
(1)式中第p+1次迭代, 滑动窗口大小为正整数Mp+1, 检测阈值是χp+1.Ri是下标为i的像素数据,i是数据下标.表示第p+1次迭代中,以下标为v的数据作为起点, 窗口大小为Mp+1的滑动窗口标记集合, 设如果Rv被检测为RFI, 则fpv= 1, 否则,fpv= 0.fpv取值为1表示p次迭代后此数据已标记为RFI数据, 反之, 此数据在当前迭代步骤被判定为非RFI数据.Count是窗口内尚未被标记为RFI像素的个数:

阈值χp+1是在VarThreshold算法阈值公式基础上,通过参数的优化来获取[16]. VarThreshod算法阈值公式为:

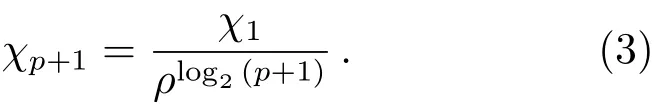
经验表明,ρ= 1.5时SumThreshold算法具有较好的效果. 为了确定阈值χ1, 可在某个给定的观测数据集上最小化错误概率实现, 在这过程中参数ρ保持不变. 确定χ1之后, 根据(3)式可计算得到各χp+1,p≥1. 文献[23]以及SEEK[21]软件中对于SumThreshold算法的阈值计算, 设置了数组η.由(3)式计算出的值除以对应的数组η值, 构成最终的阈值集合.

文献[18]对于RFI数据的判断, 未采用当前未标记为RFI像素的均值, 而是计算像素绝对值的均值. 这种RFI标记准则适用于射频干扰振荡严重,但像素平均值却接近于0的射电数据. 因此, 应当具体问题具体分析, 在不同应用背景中, 选取适宜的RFI标记准则. 本文后续内容仍然采用(1)式的RFI标记准则.

2.3.2 SumThreshold算法设计

对于某个给定宽度为Mn的检测窗口, Sum-Threshold检测的过程请见算法1:

算法1:

输入: 被检测数据长度为L, 数据集为{R0,R1, ··· , RL-1}, 算法迭代总次数为max, 窗口大小的集合{M1,M2,··· ,Mmax}, 阈值集合{χ1, χ2,··· , χmax}, 之前迭代生成的标记集合{f0, f1, ··· ,fL-1}, 标记集合元素初始化值为0

输出: 标记集合{f0,f1,··· ,fL-1}

(1)获取当前窗口大小Mn、阈值χn、初始化变量i←0、未检测为RFI的数据之和Sum←0、Count←0, 本次迭代生成的标记集合{t0, t1, ··· , tL-1}←{f0,f1,··· ,fL-1}

(2) Whilei/=Mndo

(3) Iffi== 0 then

(4) Sum←Sum +Ri

(5) Count←Count + 1

(6) End if

(7)i ←i+1

(8) End While

(9) Whilei/=Ldo

(10) If Sum/Count＞χnor Sum/Count＜-χnthen

(11) Forj ∈{i-Mn,··· ,i-1}do

(12)tj ←1

(13) End For

(14) End if

(15) Iffi== 0 then

(16) Sum←Sum +Ri

(17) Count←Count + 1

(18) End if

(19) Iffi-Mn== 0 then

(20) Sum←Sum- Ri-Mn

(21) Count←Count-1

(22) End if

(23)i ←i+1

(24) End While

(25){f0,f1,··· ,fL-1}←{t0,t1,··· ,tL-1}

步 骤(2)–(6), 计 算 从 第1个 数 据 开 始, 长为Mn的窗口内尚未被检测为RFI的像素的均值.步骤(10)–(14)判断当前窗口内像素的均值是否大于阈值, 如果判断结果为“是”, 则将当前窗口内所有尚未被检测为射频干扰的像素标记为RFI. 步骤(15)–(18)的意思是, 如果检测窗口外右侧像素在之前的迭代中未被判断为RFI数据, 则将此数据移入窗口, 窗口内数据之和以及数据个数增加. 步骤(19)–(22)的意思是如果当前窗口内左侧像素在之前的迭代中未被判断为RFI数据, 则将其移出窗口, 窗口内数据之和以及数据个数相应减少. 循环执行步骤(10)–(22), 直至所有数据被处理, 更新标记集合, 本次迭代结束.

2.3.3 基于SumThreshold算法的RFI检测示例

图8显示了一个观测数据的截面及其RFI标记结果的示例. 该数据是从某个频带中截取得到. 因此, 图8 (a)的横坐标和纵坐标分别表示时间和流量. 经过基线拟合和剔除后, 各像素的值分别为:{1, 1, 2, 1, 3, 1, 12, 14, 16, 15, 17, 20, 24, 26, 22,18, 14, 13, 11, 1, 1, 3, 3, 1, 1, 1, 2, 3, 1, 1, 1, 1}.基于SumThreshold算法进行RFI检测后, 值为{12,14, 16, 15, 17, 20, 24, 26, 22, 18, 14, 13, 11}的像素被标记为RFI (图8 (b)中斜线标记的部分).

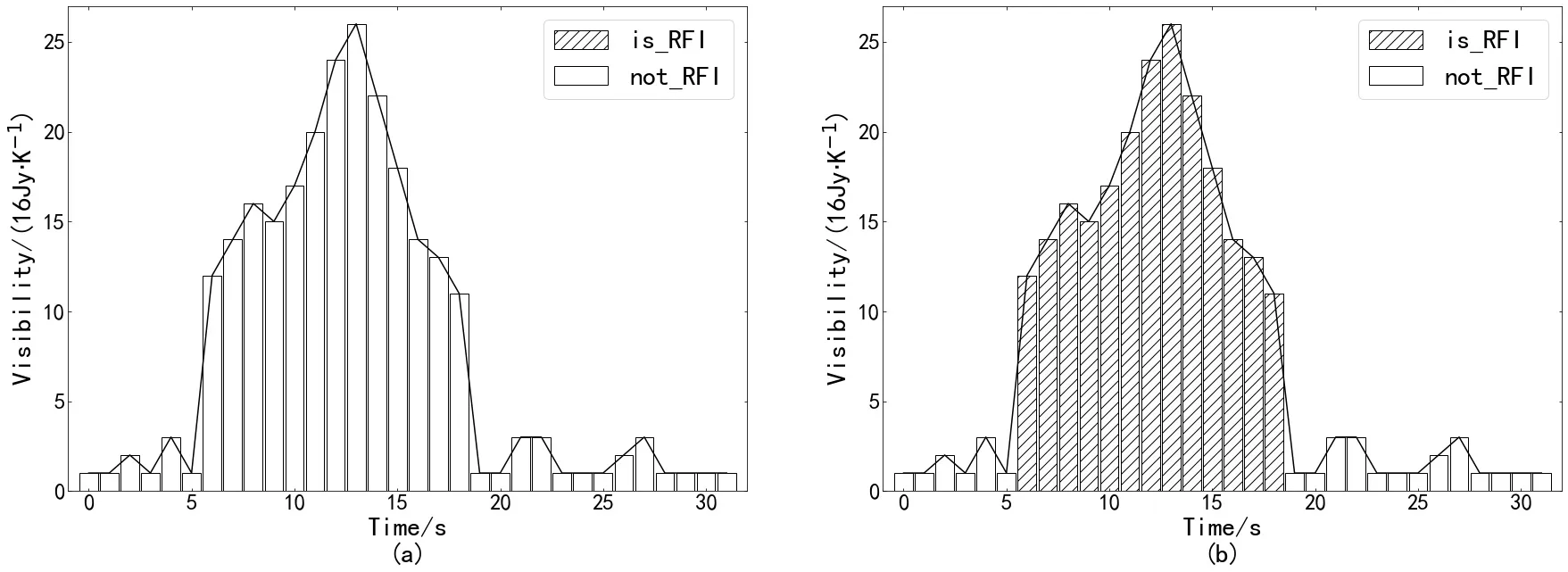
图8 一个观测数据及其RFI检测结果的截面. (a)一个观测数据的截面; (b)左图数据的RFI检测结果.Fig.8 The intersecting surface of an observation and its RFI detection results. (a) An intersecting surface of an observation; (b)an intersecting surface of RFI detection results of the left observation.

图8(a)的RFI检测过程如图9所示. 在该实验中, SumThreshold算法经过了3次迭代, 第1次迭代滑动窗口宽度是M1= 1, 阈值为χ1= 20. 迭代输入数据为图8 (a)中的数据, 如图9 (a)所示. 因为窗口大小为1, 随着窗口滑动, 每一个数据均与阈值进行比较, 值为24、26和22的数据大于阈值. 因此, 相应像素被标记为RFI (图9 (b)). 第2次迭代的滑动窗口宽度为M2= 2, 阈值是χ2= 13.3333.为了防止已标记为RFI的数据值过大导致周围的像素被错误检测为射频干扰, 在第2次迭代检测之前将第1轮迭代时被标记为RFI的像素数值改为当前阈值13.3333 (图9 (c)). 第2次迭代后新被标记为RFI的数据分别为14、16、15、17、20、18、14和13 (图9 (d)). 对于值为13的数据, 当其进入滑动窗口时, 窗口内的数据值为14和13, 该窗口内像素的均值大于阈值13.3333, 因此标记数据13为RFI. 如果将值为13的像素单独与阈值相比,则由于小于阈值而不会被检测到, 但是因为窗口内像素的整体平均效应, 该像素被SumThreshold算法标记为RFI, 解决了传统阈值法RFI由单个像素比较导致的漏检问题. 第3次迭代中窗口宽度是M3= 4, 检测阈值为χ3= 10.5180. 之前迭代中被标记为RFI的像素的值在本次迭代中置换为10.5180 (图9 (e)). 通过与第2次迭代相同操作流程, 滑动窗口对数据处理后, 新被标记为RFI的数据是值为12和11的像素(图9 (f)).

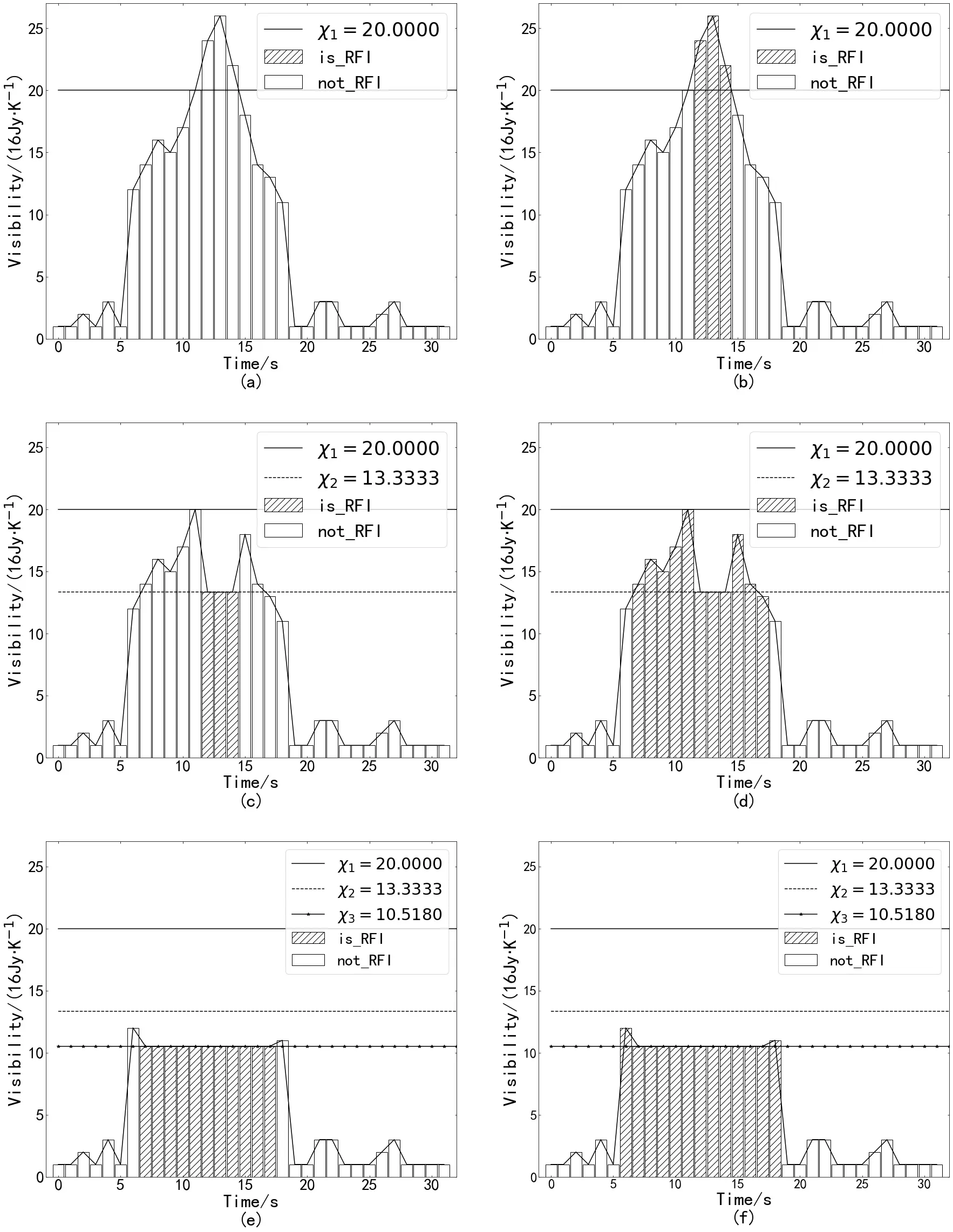
图9 RFI检测过程示例图. 图(a)、(c)、(e)分别是第1、2、3次迭代前的输入数据; 图(b)、(d)、(f)分别是第1, 2, 3次迭代处理后的数据. 详述见2.3节.Fig.9 The iterative process of RFI detection. Panels (a), (c), (e) are the input data of the iterative process and panels (b), (d),(f) are the results of the iterative process. More can be found in Sec. 2.3.

2.4 算法性能分析

2.4.1 时间复杂度

假设待检测数据长度为L, 则理论上检测窗口大小的集合为{1,2,··· ,L-1}. 每次迭代要求对每个窗口子序列大小的数据进行传递. SumThreshold算法的时间复杂度为O(L2). 这对于算法效率要求较高的应用很难满足要求. 因此, 基于指数增长设定窗口大小, 则检测窗口集合成为原始窗口集合的子集. 例如, 若将窗口大小设为[1,2,4,8,16,···],则算法时间复杂度为O(Llog2L). 与理论上的检测窗口集合相比, 减少了尺寸为[3,5,6,7,···]的窗口.这些被减少的窗口所检测的数据特征, 仍可能被约简窗口集合检测到. 因此, 上述对候选窗口减少的做法对算法精度不产生显著影响.

在减少候选检测窗口集合的基础上, 设定数据集子集大小, 可进一步将算法复杂度降低. 在文献[24]中, 通过限定数据子集小于1024, 算法效率明显提高. 但是算法的精度会受影响, 这是因为非常微弱或者范围大的特征将被忽略.

2.4.2 算法适用性

已有研究表明, SumThreshold算法是射电数据RFI检测的有效方法, 适合所有类型的RFI检测.根据各类RFI的特性可知, 基于频率方向的检测适用于带状射频干扰, 基于时间方向的检测则对突发脉冲射频干扰效果较好[15]. 基于时间和频率双向的检测, 可检测复合干扰. 与其他阈值类RFI检测算法一样, SumThreshold算法对带状RFI和复合型RFI检测均受射电数据频率子带大小的影响[15].

2.4.3 算法精度

SumThreshold算法对射电数据进行RFI标记,结果可分为4类: 真阳性(True positive, TP): 标记为RFI的数据, 实际上也是RFI数据; 假阳性(False positive, FP): 标记为RFI的数据, 实际上不是RFI数据; 真阴性(True negative, TN): 标记为非RFI的数据, 实际上也是非RFI数据; 假阴性(False negative, FN): 标记为非RFI的数据, 实际上是RFI数据. 这4类结果可构成混淆矩阵, 见表1.

基于表1, 射频干扰检测结果的常用精度度量指标有:

表1 RFI检测混淆矩阵Table 1 Confusion matrix of RFI detection

(1)真阳率(True positive rate, TPR):RFI被正确检测的概率.

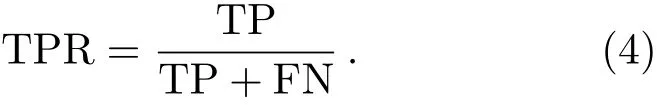
(2)假阳率(False positive rate,FPR):非RFI数据中, 被标记为RFI数据的概率.

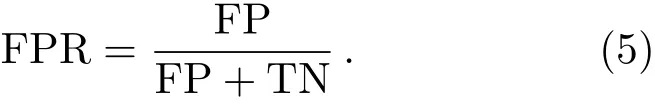
(3)假阴率(False negative rate, FNR): RFI数据中, 被标记为非RFI数据的概率.

(4)准确率(Accuracy): 正确标记的RFI数据和非RFI数据占全部数据的比例.

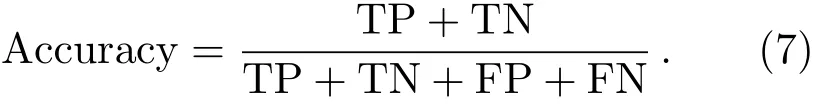
(5)精确率(Precision): 正确标记为RFI的数据占全部标记为RFI数据的比例.

SumThreshold算法在RFI检测中具有较高的精度. 文献[16]基于真阳率和假阳率对Sum-Threshold、SVD和VarThreshold等RFI检测方法做了比较研究(详见该文献的图8), 结果发现SumThreshold算法在RFI检测中具有更高的精度.这主要是因为, SVD方法无法判断数据幅度的平稳增加是否是由RFI导致, 从而使它在检测中易产生错误.图10为SumThreshold算法和VarThreshold算法的频率-时间双向RFI检测结果对比, 由于RFI检测策略不同, 使得SumThreshold算法和VarThreshold算法的RFI检测结果不相同. 实际上, Var-Threshold算法的RFI检测结果是SumThreshold算法RFI检测结果的子集(图10 (c)和(d)), SumThreshold算法更易检测出各类RFI数据.

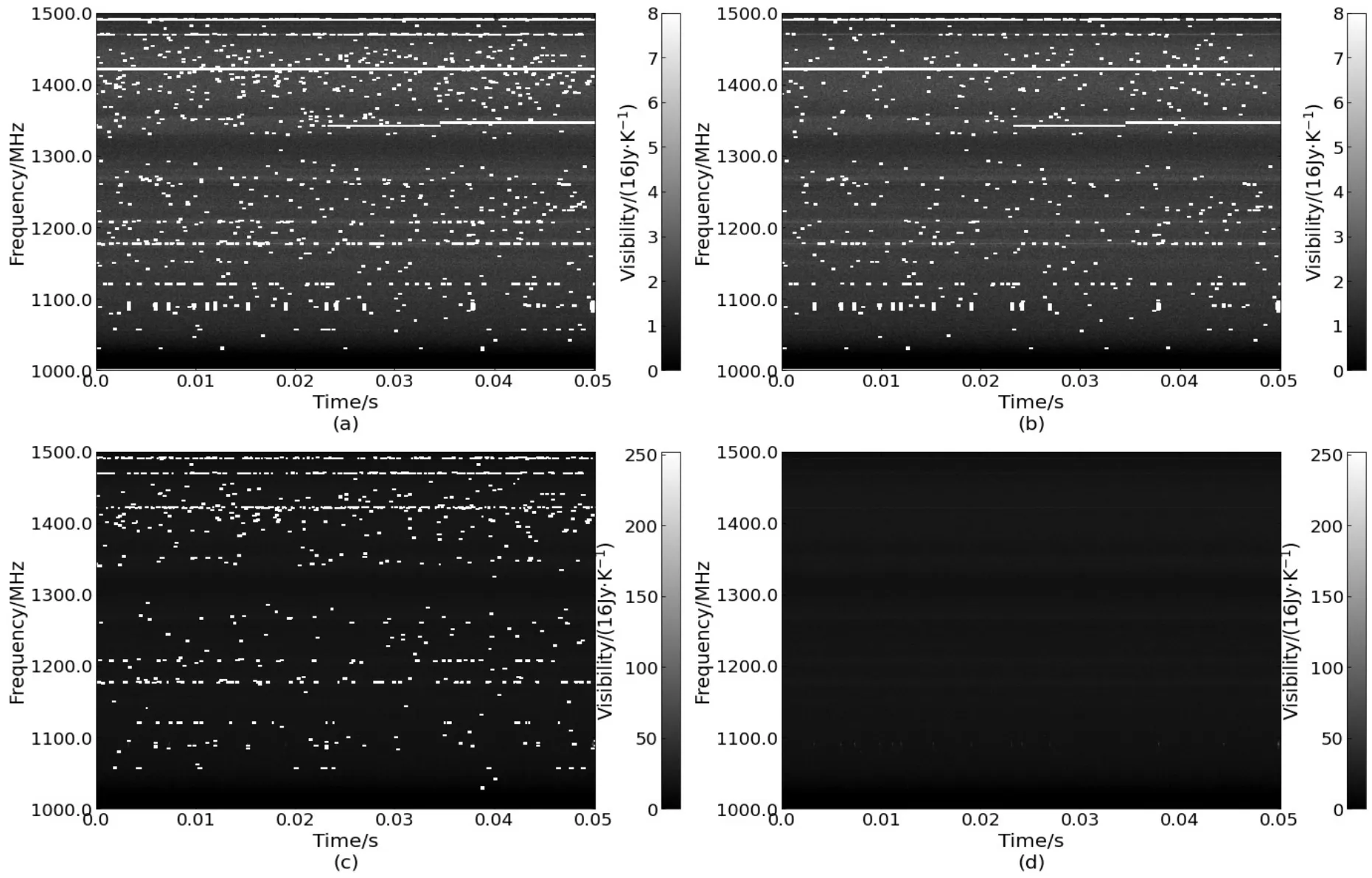
图10 SumThreshold算法和VarThreshold算法的频率-时间双向RFI检测结果对比. (a) SumThreshold算法(采用频率-时间双向检测策略)的RFI检测结果; (b) VarThreshold算法(采用频率-时间双向检测策略)的RFI检测结果; (c) SumThreshold算法检测到但未被VarThreshold算法检出的RFI; (d) VarThreshold算法检测到但未被SumThreshold算法检出的RFI. 该数据来源于FAST观测[23].Fig.10 Comparison between the RFI detection results of SumThreshold and VarThreshold. (a) The RFI detection result using SumThreshold with frequency-time bidirection scheme; (b) the RFI detection result using VarThreshold with frequency-time bidirection scheme; (c) the RFI detected by SumThreshold method, but not by VarThreshold method; (d) the RFI detected by VarThreshold, but not by SumThreshold method. The experimental data are of a FAST observation[23].

基于2.3节RFI检测的示例数据, SumThreshold算法和VarThreshold算法的RFI检测对比结果如图11. 通过定量对比发现, VarThreshold算法更容易出现漏标记的现象. 同时文献[12]指出Sum-Threshold算法假阳率的定量化计算更为简单, 使得它在大规模观测数据中检测RFI时更为高效.

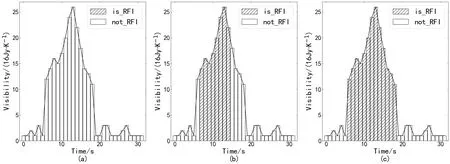
图11 VarThreshold算法和SumThreshold算法RFI检测对比图. (a)一个观测数据的截面; (b) VarThreshold算法RFI检测结果; (c)SumThreshold算法RFI检测结果.Fig.11 Comparison between the RFI detection results of VarThreshold and SumThreshold. (a) An intersecting surface of an observation; (b) the intersecting surface of the RFI detection result using VarThreshold method; (c) the intersecting surface of the RFI detection result using SumThreshold method.

3 SumThreshold算法优化

3.1 形态学算子

在有些情况下, 干扰源的接收功率会随着时间和频率产生变化. 这使得即使连续地接收同一个干扰源的数据, 也会因接收功率的变化, 导致阈值检测方法无法在整个范围内检测到干扰源. 图12是SumThreshold算法未做膨胀操作的RFI检测结果. 该检测结果中存在大量干扰源接收功率变化造成的带状干扰断裂. 对此, 可利用形态学方法将高聚集RFI数据周围的数据进一步做RFI标记, 消除断裂.

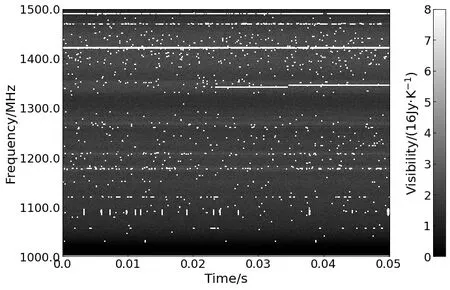
图12 SumThreshold算法未做膨胀操作的RFI检测结果. 该检测结果中存在大量干扰源接收功率变化造成的带状干扰断裂. 该数据来源于FAST观测[23].Fig.12 The RFI detection results using the SumThresold without morphology-based flagging. The figure shows negative effects from the unstableness of received power from interfering sources. The experimental data are of a FAST observation[23].

文 献[19]在 对LOFAR (Low Frequency Array)观测数据进行RFI检测的研究中发现, 普通的膨胀操作对尖锐的射频特征较为敏感, 易将非射频干扰数据误判为RFI; 同时, 通常的膨胀操作对平滑的射频特征不敏感, 使得RFI数据存在漏标现象. 因此, 传统膨胀方法无法有效解决RFI检测中的断裂或边缘漏检测问题. 因此, 文献[19]引入新的膨胀算子: 尺度不变秩(Scale Invariant Rank,SIR)算子. 在使用SumThreshold算法进行RFI检测后, 进一步基于SIR算子对检测结果做后处理, 在时域、频率或是两者结合的方向上选取若干个大小不一的滑动窗口逐行扫描, 计算滑动窗口内的置信度. 置信度是判断滑动窗口内样本是否应该进一步被标记为RFI的指标. 当置信度大于指定阈值时, 将当前滑动窗口内的样本标记为RFI. 反之, 如果置信度小于给定的阈值, 则当前窗口内的样本不会被标记为RFI. 置信度更新的准则为: 从左到右对滑动窗口内样本进行遍历, 当样本已被标记为RFI时, 置信度值加1, 反之, 置信度值不变.

SIR算子的引入进一步提高了RFI检测结果的精度. 基于高斯频率分布的宽带RFI特征模拟如图13所示.图13中当图像中加入噪声,影响了RFI的可辨识度; 这时在噪声数据上运行SumThreshold算法会产生RFI标识的漏标, RFI检测准确率为41.56%. 在SumThreshold算法检测基础上, 引入SIR算子, 通过图13 (c)和(d)对比可以看出, SIR算子提高了检测的精度, RFI检测准确率提高为59.53%. 但是不足在于, SIR运算显著地增加了算法的运行时间.

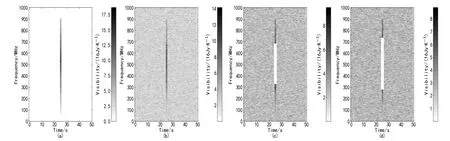
图13 基于高斯频率分布的宽带RFI特征模拟图. (a)单独RFI图像; (b)加入噪声的RFI图像; (c)基于SumThreshold的RFI检测结果; (d)基于SumThreshold + SIR操作的RFI检测结果. 基于文献[19]设计完成本实验.Fig.13 Simulation of a typical broadband RFI feature with Gaussian frequency profile. (a) Isolated RFI feature; (b) when noise is added, a part of the feature becomes undetectable; (c) flagged with the SumThreshold method; (d) with SIR operator applied.This experiment is designed based on Ref.[19].

3.2 多特征检测

SumThreshold算法主要是根据时频观测数据中的信号强度进行RFI检测. 实际上, 观测数据具有多种特征, 例如, 时间累计图和相位等, 这些特征中均包含数据的有用信息. RFI数据与非RFI数据由于性质差异, 在不同特征上会表现出不同的数据特点. 例如, 文献[16]研究发现, 未污染数据中相位接近零旋转, 而RFI数据具有偏移为零的相位.因此, 相位包含有价值的RFI检测信息, 针对多特征进行基于SumThreshold的RFI检测可提高算法精度.

3.3 基于图形处理器(Graphics processing unit, GPU)的算法移植

随着图形处理元件的发展, 图形处理器的应用越来越广泛. GPU计算相比于中央处理器(Central processing unit, CPU)具有并行度高、内存带宽高和运行速度快等优势. 因此, 已有学者[15]将SumThreshold算法移植到GPU平台. 由于体系结构之间的差异, 在GPU平台中对原始算法进行了修改, 实现了基于GPU的小粒度并行处理. 基于GPU的改进算法在速度和精度上均具有优良的性能, 可实现RFI的在线检测.

4 总结

SumThreshold算法作为典型的阈值类RFI检测方法, 在射电数据处理中已有广泛的应用. 本文对SumThreshold算法进行了详细阐述, 介绍了算法的原理和流程, 分析了算法的关键步骤和设计实现. 通过检测示例, 直观、详尽地讨论了SumThreshold算法进行RFI检测的过程. 性能分析表明, 此算法可有效检测各类型RFI, 满足在线分析等高性能应用需求. 针对算法的优化, 本文从形态学算子、多特征选取、算法移植等角度分别做了总结和论述.

在未来的工作中, 将根据关键科学数据处理的需求进行SumThreshold算法的改进研究, 尤其是FAST数据的RFI检测. FAST作为世界上口径最大和最灵敏的单口径射电望远镜, 它为众多科学发现提供了前所未有的机遇. 在国家重大需求方面,FAST具有重要的应用价值[25]. 因此, 有必要研究SumThreshold算法在FAST数据RFI 检测方面的应用.

致谢感谢审稿人对文章提出的宝贵建议, 使得文章的质量有了显著的提高.