飞机舱门密封系统的仿真分析与优化设计

姚文心，徐鸣遥，袁永平

（沈阳航空航天大学 民用航空学院，辽宁 沈阳 110136）

飞机舱门（简称舱门）密封系统对飞机的整体性能起着至关重要的作用。目前，飞机的性能飞速提升，而舱门密封的设计仍比较传统[1-2]，常见的舱门密封系统的结构如图1所示。因此，舱门密封的设计仍有很大的进步空间，需要不断地创新。随着密封形式的不断发展完善，舱门密封会变得更加安全可靠、更能满足时代要求[3-5]。近年来，国内外一些学者对舱门密封系统的结构进行了研究，期望得到更加安全可靠的舱门密封系统。王楠[6]依据可靠性原理，对舱门密封装置进行了试验研究，总结了舱门密封结构参数对其密封性能的影响。渠涛等[7]研究了在不同条件下，不同截面形状的舱门密封带的性能，推荐了不同结构的舱门密封装置。马莹[8]对各种载荷作用下舱门密封结构的位移进行了研究。马超[9]对舱门密封形式及材料进行了研究。王增辉[10]对舱门密封带进行了仿真分析，研究了织物材料和舱内增压对舱门密封带的压缩应力和接触应力的影响。H.YAN等[11]基于多体动力学和弹性理论，建立了增加摩擦载荷的刚柔体模型。B.F.GOULARTE等[12]研究了作用在舱门弹性密封件上的压力。T.ROMING[13]研究了内外两层密封结构及降低两层密封结构间压力的减压装置。

图1 舱门密封系统的结构示意Fig.1 Structure diagram of sealing system of cabin door

本工作运用Abaqus有限元分析软件和Solidworks三维建模软件，对舱门密封系统进行仿真分析，得到其压缩应力和最大接触应力；利用数学主成分分析法对舱门密封系统从结构和材料两方面进行正交试验，建立试验对照组，进行仿真试验，对比分析舱门密封系统的影响因子对其密封性能的影响程度，并对密封带进行优化设计。

1 三维建模

本工作选取某型号的飞机前货舱舱门结构作为研究对象[14]，为在有限元分析中既能节省迭代计算时间，又能保证实际结构不发生改变，且对分析结论不产生较大的偏差，利用Solidworks软件建立了舱门、密封带和机身的三维模型，如图2所示。

图2 舱门密封系统的三维模型Fig.2 3D model of sealing system of cabin door

为进一步提高分析效率，对舱门密封系统模型进行了切片简化处理。

2 有限元仿真分析

2.1 模型分析

舱门密封系统的有限元模型如图3所示。其中，舱门和机身均为结构钢材料，弹性模量为70 GPa，泊松比为0.29；密封带截面形状均一，内部为空心结构，材料为硅橡胶材料。

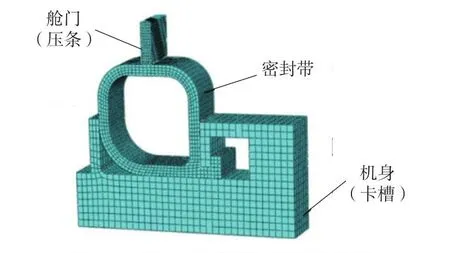
图3 舱门密封系统的有限元模型Fig.3 Finite element model of sealing system of cabin door

在Abaqus软件中修改模型、定义装配件及其接触相互作用、设置载荷和边界条件，提交有限元分析结果。其中，模型划分网格为C3D8H单元（八节点线性六面体单元），具体网格划分参数如表1所示[15]。

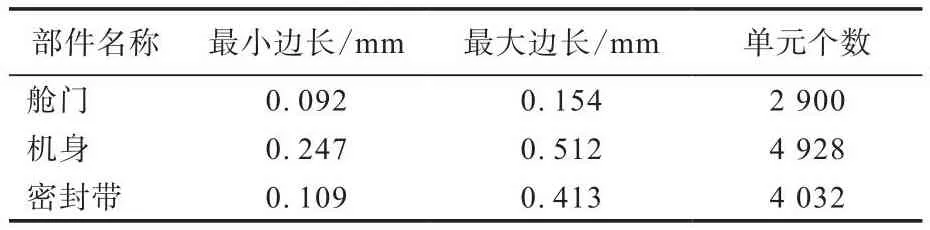
表1 舱门密封系统的各部件网格划分参数Tab.1 Mesh division parameters of components of sealing system of cabin door

2.2 分析结果

计算完成后，先点击作业按钮，再点击提交求解界面的结果按钮，进入可视化模块进行结果查看，得到舱门密封结构的应力云图和位移云图，分别如图4和5所示。

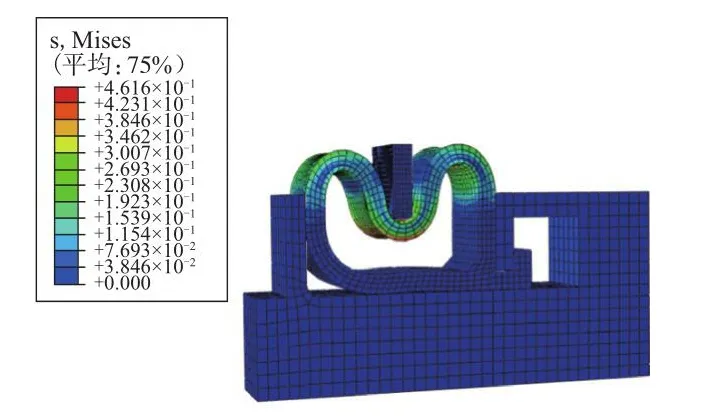
图4 舱门密封系统的应力云图Fig.4 Mises nephogram of sealing system of cabin door

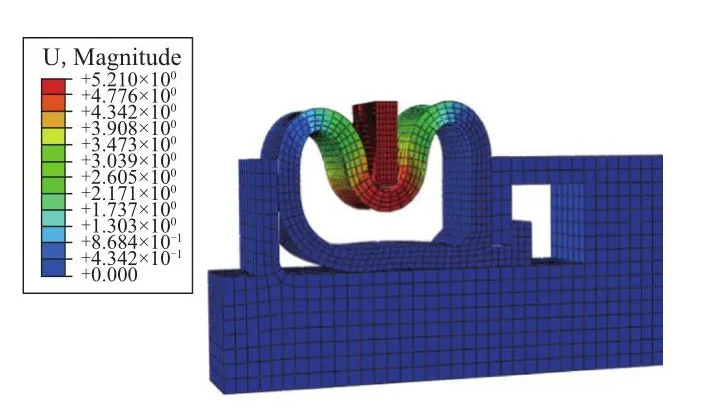
图5 舱门密封系统的位移云图Fig.5 Displacement nephogram of sealing system of cabin door

3 舱门密封系统的优化设计

舱门密封带的结构和材料（包括橡胶材料和增强织物等）是其密封系统的气密性的主要影响因素，本工作选取舱门密封带的结构和材料作为研究对象。借鉴国外舱门密封带的设计经验（密封带厚度为0.8～3.0 mm）[13]，本工作取密封带的厚度为0.8 mm。

3.1 参数设置

舱门密封系统的设计参数包括密封带的截面圆角半径（因子A）、橡胶材料邵尔A型硬度（因子B）、橡胶材料属性（因子C）、有无增强织物（因子D）和压缩位移（因子E）。研究中，在保持舱门密封系统其他参数不变的情况下，调节其中一个参数，观察其对舱门密封性能的影响。其中，关闭舱门所需的力定义为压缩应力，其大小决定了关门所需推力的大小；舱门密封系统所能承受的最大接触应力决定舱门密封系统的密封效果。舱门密封系统承受的压缩应力越小，关闭舱门所需推力越小；舱门密封系统承受的最大接触应力越大，舱门密封系统的密封性能越好。

对舱门密封带的各设计参数进行有限元仿真分析，得到对应舱门密封系统的压缩应力和最大接触应力数据，从而得出优化结论。

舱门密封系统的正交试验设计参数见表2。

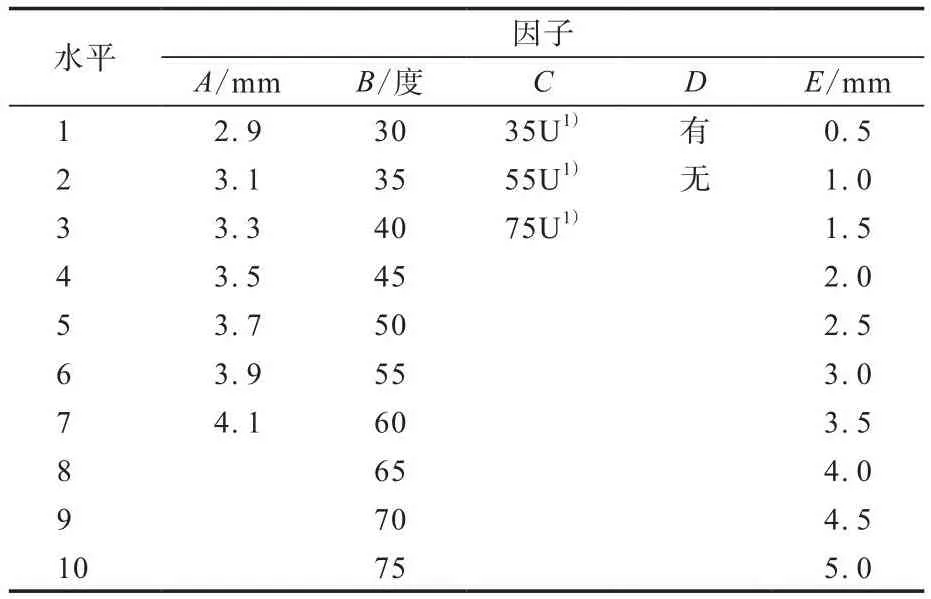
表2 舱门密封系统的正交试验设计参数Tab.2 Orthogonal experimental design parameters of sealing system of cabin door

根据仿真分析结果，提取密封带的压缩位移为0.5～5 mm时的舱门密封系统的压缩应力和最大接触应力，分析密封带内部增强织物及橡胶材料属性对舱门密封性能的影响；同时提取密封带的压缩位移为5 mm时舱门密封系统的压缩应力和最大接触应力，分析密封带的截面圆角半径及橡胶材料邵尔A型硬度对舱门密封性能的影响。

3.2 优化方法

改变密封带的截面圆角半径和在密封带内层加入一层增强织物，研究密封带结构对舱门密封性能的影响；选择35U，55U和75U三种牌号硅橡胶材料，研究密封带的橡胶材料属性对舱门密封性能的影响；选取10种邵尔A型硬度的硅橡胶材料，分析密封带的橡胶材料硬度对舱门密封性能的影响。利用Matlab平台对试验数据进行处理，分析舱门密封系统的影响因子对舱门密封性能的影响程度，并对舱门密封系统进行优化。

4 舱门密封系统设计参数的影响分析

4.1 因子A对舱门密封性能的影响

选择邵尔A型硬度为70度的35U硅橡胶材料、内部有增强织物的密封带，改变因子A（分别为2.9，3.1，3.3，3.5，3.7和3.9 mm，对应试验方案为A1—A6），对密封带结构进行有限元仿真分析，结果如表3所示。

表3 因子A对舱门密封性能的影响Tab.3 Influence of factor A on sealing performances of cabin doors MPa

从表3可以看出，因子A为3.5 mm时舱门密封系统的压缩应力最小，最大接触应力最大，因此因子A为3.5 mm时关闭舱门最省力，且舱门密封效果最好。

4.2 因子D对舱门密封性能的影响

依据表2的设计参数，采用缩减有限元仿真模型法，设置试验组如下：保证因子A（3.5 mm）不变，改变因子C（分别为35U，55U，75U），在内部无增强织物时因子与水平的试验组合分别为A4C1D2，A4C2D2，A4C3D2，在内部有增强织物时因子与水平的试验组合分别为A4C1D1，A4C2D1，A4C3D1。进行有限元仿真分析后，得到各试验组合舱门密封系统的压缩应力和最大接触应力分别如表4和5所示，利用Matlab平台对试验数据进行可视化处理，各试验组合舱门密封系统的压缩应力和最大接触应力曲面分别如图6和7所示。

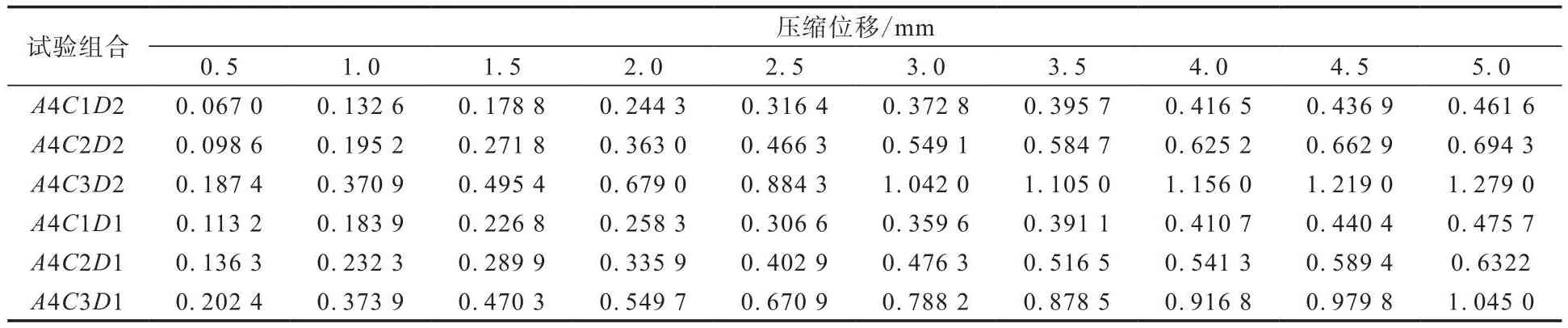
表4 各试验组合舱门密封系统的压缩应力分析结果Tab.4 Compression stress analysis results of sealing systems of cabin doors for various experimental combinations MPa

表5 各试验组合舱门密封系统的最大接触应力分析结果Tab.5 Maximum contact stress analysis results of sealing systems of cabin doors for various experimental combinations MPa

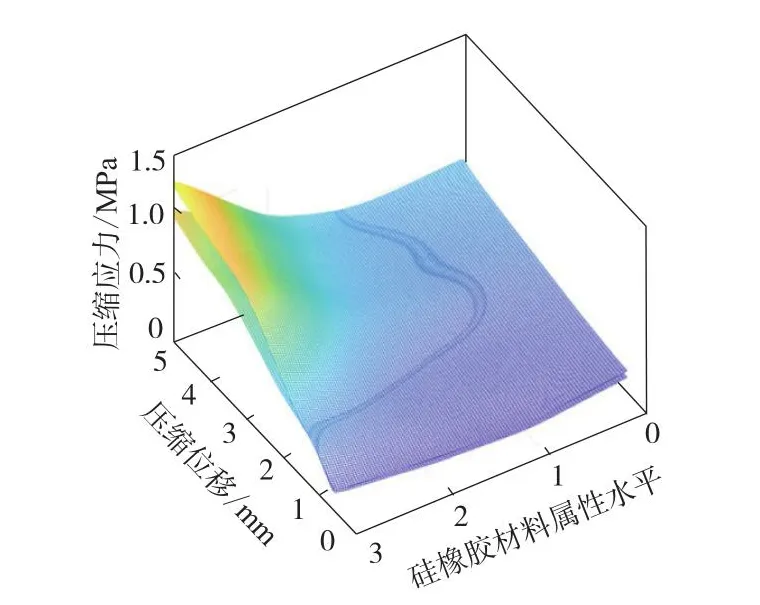
图6 各试验组合舱门密封系统的压缩应力曲面Fig.6 Compression stress surfaces of sealing systems of cabin doors for various experimental combinations

从图6可以看出：舱门密封系统的压缩应力存在两个曲面，上曲面为密封带内部有增强织物时舱门密封系统的压缩应力，下曲面为密封带内部无增强织物时舱门密封系统的压缩应力；与密封带内部无增强织物时舱门密封系统相比，密封带内部有增强织物时舱门密封系统的压缩应力较大，故密封带内部有增强织物时舱门密封系统的关门力有所增大；随着密封带压缩位移的增大，上下两曲面逐渐靠近，呈相合趋势，故密封带内部是否有增强织物对舱门密封系统的压缩应力影响很小，因此密封带的结构优化时内部是否增加增强织物以其最大接触应力结果为准。

从图7可以看出：舱门密封系统的最大接触应力存在两个曲面，上曲面为密封带内部有增强织物时舱门密封系统的最大接触应力，下曲面为密封带内部无增强织物时舱门密封系统的最大接触应力；与密封带内部无增强织物时舱门密封系统相比，密封带内部有增强织物时舱门密封系统的最大接触应力明显增大，使得舱门密封性能有所提升。

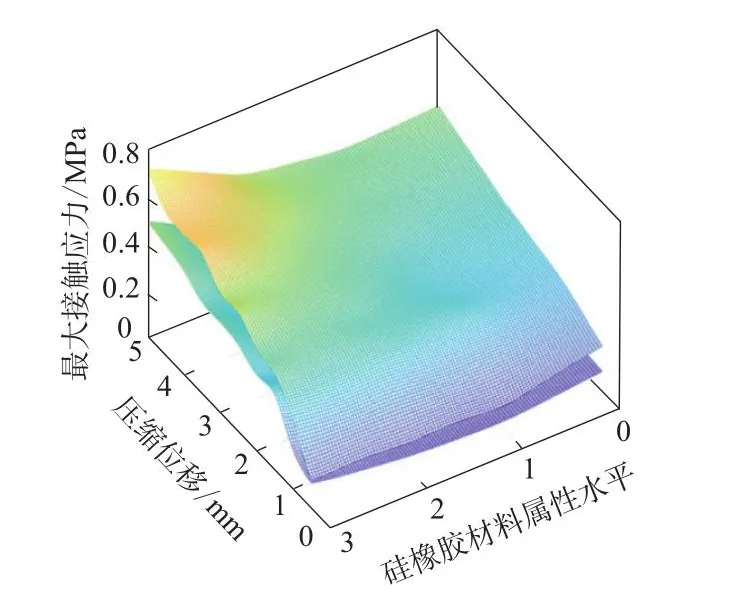
图7 各试验组合舱门密封系统的最大接触应力曲面Fig.7 Maximum contact stress surfaces of sealing systems of cabin doors for various experimental combinations

密封带内部有增强织物使舱门密封系统所受的压缩应力有所增大，但由于影响较小，可以忽略不计。与密封带内部无增强织物相比，密封带内部有增强织物对舱门密封系统的最大接触应力影响较大，舱门密封系统的最大接触应力明显增大，密封性能显著提升，故密封带应采用内部有增强织物的优化设计。

4.3 因子C对舱门密封性能的影响

利用Matlab平台对表4和5中的数据进行精细化处理，因子C对舱门密封系统的压缩应力和最大接触应力的影响分别如图8和9所示，其中35U＋ZC表示密封带为35U硅橡胶材料、内部有增强织物，其余类同。

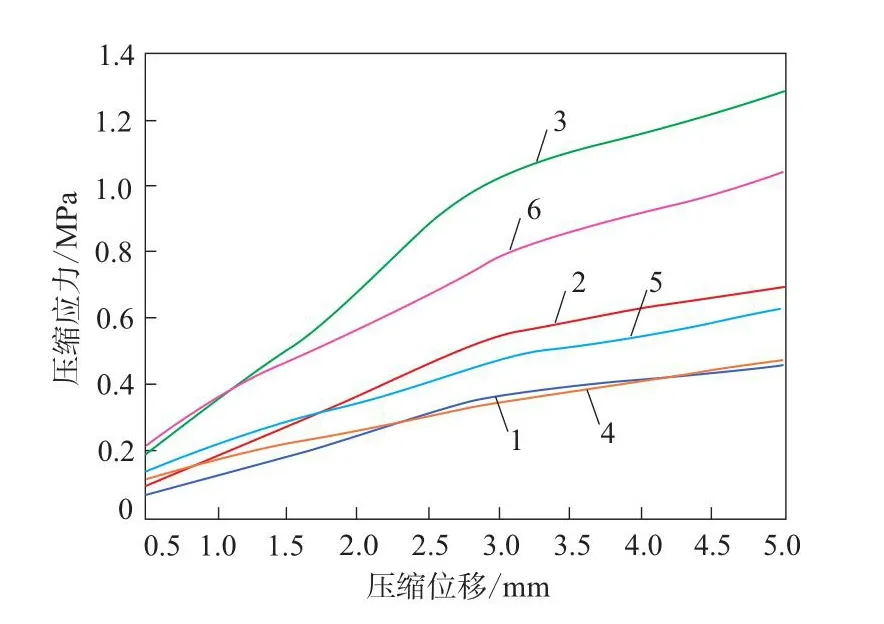
图8 因子C对舱门密封系统压缩应力的影响Fig.8 Influence of factor C on compression stresses of sealing systems of cabin doors

从图8可以看出：舱门密封系统的压缩应力随着密封带的压缩位移的增大而增大；密封带内部有增强织物时舱门密封系统的压缩应力最大的试验组合为C3D1，最小的试验组合为C1D1，即密封带内部有增强织物并采用35U硅橡胶材料时舱门密封系统的压缩应力最小。

从图9可以看出：舱门密封系统的最大接触应力随着密封带的压缩位移的增大而增大；密封带内部有增强织物时舱门密封系统的最大接触应力最大的试验组合为C3D1，最小的试验组合为C1D1，即密封带内部有增强织物并采用75U硅橡胶材料时舱门密封系统的最大接触应力最大。

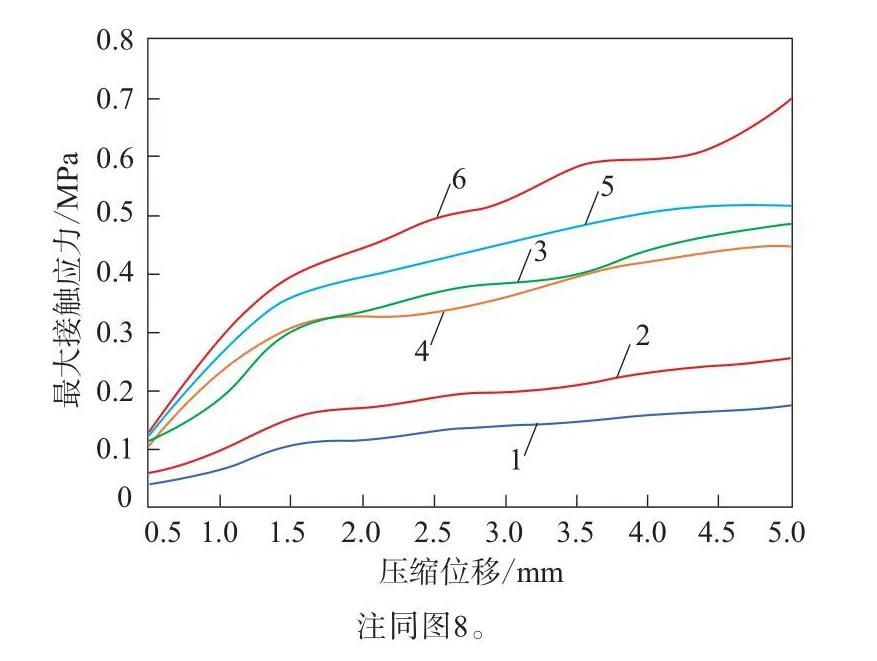
图9 因子C对舱门密封系统最大接触应力的影响Fig.9 Influence of factor C on maximum contact stresses of sealing systems of cabin doors

综上可知，在密封带内部有增强织物并采用35U硅橡胶材料时舱门密封系统的压缩应力最小，而密封带内部有增强织物并采用75U硅橡胶材料时舱门密封系统的最大接触应力最大，考虑舱门压力与密封效果的共同要求，密封带采用55U硅橡胶材料。

4.4 因子A和B综合分析

将各因子整合进行分析，在密封带内部有增强织物条件下，改变因子A和B对舱门密封系统进行有限元仿真分析。因子A和B对舱门密封系统的压缩应力曲面和最大接触应力曲面的影响分别如图10和11所示。

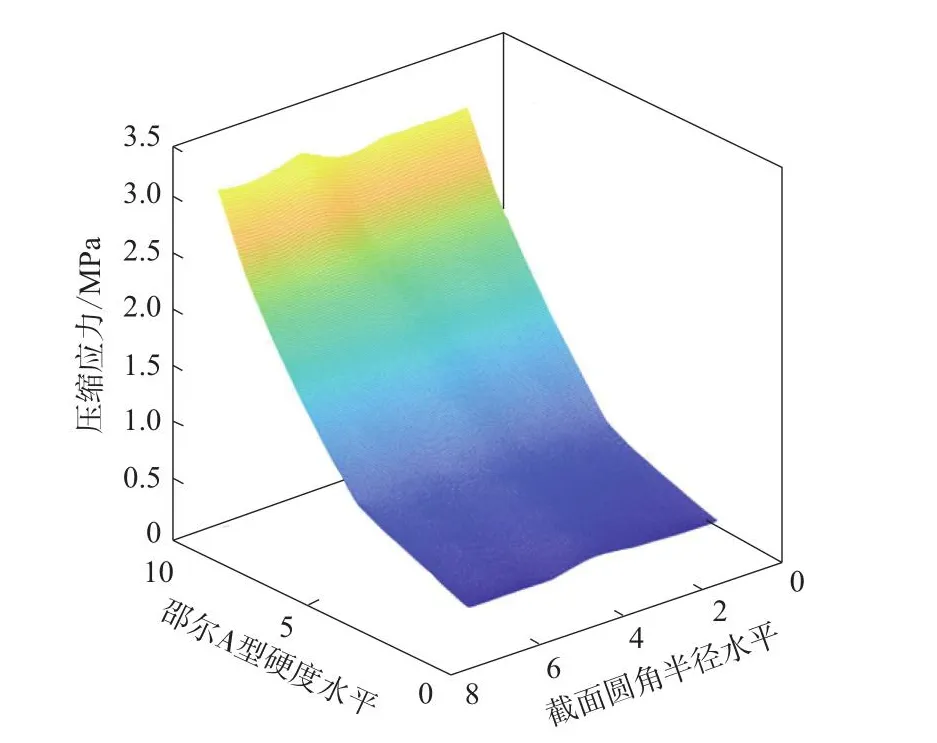
图10 因子A和B对舱门密封系统压缩应力曲面的影响Fig.10 Influence of A and B factors on compression stress surface of sealing system of cabin door

从图10可以看出：曲面颜色随着密封带的硅橡胶材料邵尔A型硬度的增大而逐渐变浅，代表舱门密封系统的压缩应力随着密封带的硅橡胶材料邵尔A型硬度的增大而逐渐增大；曲面颜色随着密封带的截面圆角半径的变化而变化不明显，但密封带的截面圆角半径为3.5 mm时曲面颜色最深，代表密封带的截面圆角半径为3.5 mm时舱门密封系统的压缩应力最小。

从图11可以看出：曲面颜色随密封带的硅橡胶材料邵尔A型硬度的增大而逐渐变浅，代表舱门密封系统的最大接触应力随着密封带的硅橡胶材料邵尔A型硬度的增大而逐渐增大；随着密封带的截面圆角半径变化，曲面颜色变化不一，但密封带的截面圆角半径为3.5 mm时舱门密封系统的最大接触应力最大。

图11 因子A和B对舱门密封系统最大接触应力曲面的影响Fig.11 Influence of A and B factors on maximum contact stress surface of sealing system of cabin door

综上可知，随着密封带的硅橡胶材料邵尔A型硬度的增大，舱门密封系统的压缩应力和最大接触应力均增大，兼顾舱门密封系统的关门力和密封效果，本工作选择密封带的硅橡胶材料的邵尔A型硬度为50度。在密封带的截面圆角半径为3.5 mm时舱门密封系统的压缩应力最小，最大接触应力最大，故密封带的最佳截面圆角半径为3.5 mm。

优化后舱门密封系统的三维模型及应力云图分别如图12和13所示。

图12 优化后舱门密封系统的三维模型Fig.12 3D model of optimized sealing system of cabin door

图13 优化后舱门密封系统的应力云图Fig.13 Mises nephogram of optimized sealing system of cabin door

5 结论

本工作利用Abaqus软件对舱门密封系统进行仿真分析，运用Matlab平台对试验数据进行处理、绘出图像，分析密封带的截面圆角半径、橡胶材料硬度和属性以及内部增强织物对舱门密封性能的影响，结果得出当密封带的截面圆角半径为3.5 mm、采用邵尔A型硬度为50度的55U硅橡胶材料、内部有增强织物时，舱门密封系统的密封性能最优。