一道高考最值问题的多视角解答与反思

魏东升

(厦门双十中学漳州校区,福建 漳州 363107)

笔者在一节关于“阿波罗尼斯圆的性质及应用”的专题课中给出了一道有关解三角形面积最值的问题,这个问题原本是为了当堂检测学生对课堂知识的掌握情况,也就是希望同学们能够运用阿波罗尼斯圆来解决,但是同学们出彩的表现让笔者惊叹.为方便呈现解决问题的思维过程,引原题如下.

1 问题的呈现

这道短小精悍的解三角形面积的最值问题其实是一道经典的高考真题,它出自2008年高考江苏卷第13题．说它经典,一方面是因为其虽为解三角形的问题,却可以用解析几何中的相关知识快速解决,体现了数学知识之间的紧密联系;另一方面,由于其和阿波罗尼斯圆之间的微妙关系,使得许多数学教师在讨论阿波罗尼斯圆时几乎都绕不开它.

根据课堂上同学们的反馈,笔者将从三个视角对其解析.

2 问题的解决

视角1 角度.

计S△ABC为S,在△ABC中,由余弦定理,得

这个面积表达式其实是一个分式三角函数,对于其最值的处理,同学们给出了三种思路:

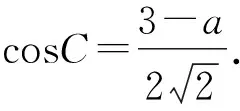
代入上式,得

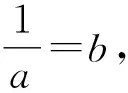
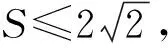
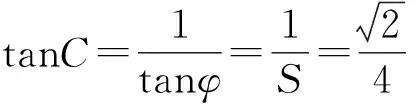
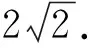
在高中数学的学习中,分式三角函数最值问题其实不算特别常见,但同学们的表现可谓亮眼,思路1先是利用平方以化同名,然后进行多次换元,最终转化为二次函数最值问题;思路2则是把最值问题转化为方程有解问题,利用三角函数的有界性;而思路3更绝,直接想到了S的几何意义,把最值问题转化为线性规划问题来处理.这三种处理手段再次验证了解决最值问题的多种转化手段:转化为函数的最值、不等式的解集、方程有解等问题.

视角2长度.

在△ABC中,由余弦定理,得

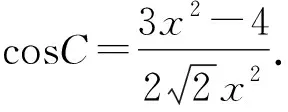
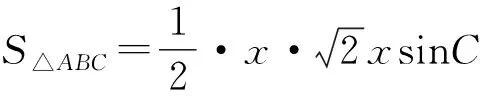
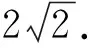
较之用角度表示面积,用长度表示的方式显然更为便捷,可谓选择大于努力!需要补充的是,除了上述方式可以得到用长度来表示面积,还可以利用秦九昭公式或海伦公式直接得到.

不管是用正弦定理还是余弦定理,解答起来都离不开强大的运算能力,有更好的解决办法吗?能不能通过构建直角三角形以便于应用勾股定理?

在△ACD和△BCD中,由勾股定理,得

h2+y2=x2,

h2+(y+2)2=2y2.

消去x,得h2=-(y-2)2+8≤8,

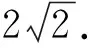
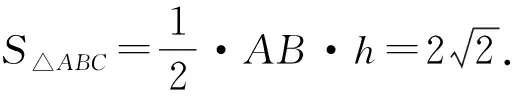
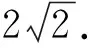
这种思路完美地避开了因为用正弦定理或余弦定理导致的运算量,可谓妙也!

解法4 过点C作∠BCD=∠BAC交AB的延长线于点D,则△ACD∽△BCD.

由BD=2知点D是定点.

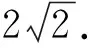
原来点C的轨迹是一个圆,这个解法简直完美!如果要像解法3一样用一个字来形容,就是绝!不仅想法独特,而且运算量几乎为零,另外点C的轨迹是圆这个事实更是起到了抛砖引玉的作用,因为她让不少同学又开始往解析几何的方向想去.

视角3坐标.

解法5 以AB所在直线为x轴,AB的中垂线为y轴,则A(-1,0),B(1,0).

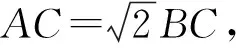
整理,得 (x-3)2+y2=8.

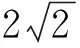
假设AB边上的高为h,

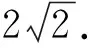
这种解法其实是求曲线轨迹方程中的直译法[1].这样一来解题的思路就已经到了求曲线的轨迹方程这里,考虑到点C是AC和BC的交点,于是又有同学提出了交轨法.

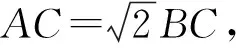
结合直线AC和BC的方程消去k1和k2,得

(x-3)2+y2=8.

在感受了同学们不俗的表现后,让我们“回归初心”,一起看看大多数同学在学习了本堂课之后利用阿波罗尼斯圆得到的解法.在给出这种解法前,先给出阿波罗尼斯圆的一个定理.

定理在图1中,A,B是距离为2a的两点,P,Q分别为线段AB的定比为λ(λ≠1)的内外分点,则以PQ为直径的圆D上任意点到A,B两点的距离之比为λ．

图1 阿波罗尼斯圆

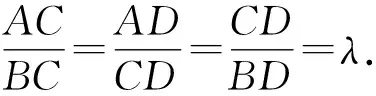
这样就有了第7种解法.

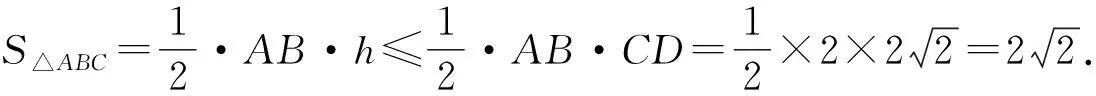
3 解后的反思

原本是希望同学们通过这道题来感受阿波罗尼斯圆在解题中的妙用,却不曾想许多同学并没有按“常理”出牌,在“打破”老师预设的同时,集体奉献了一桌丰盛的解题大餐.在感叹于学生们思维敏捷的同时,笔者心里不禁暗暗自问:假如自己没有给学生们更多思考的余地,这节课也一定能在自己的掌控中“胜利”完成,可如果这样的话,自己还能享受到这道令人难忘的解题盛宴吗?这也不禁让自己对在教学中如何提高学生解决问题的能力,从而最终提升其数学核心素养产生了新的思考.

要提高解决问题的能力,就应该先提升学生提出问题的能力[3].因为有了提出问题的能力,也就有了解决问题的动力.但事实上提出问题往往比解决问题更难,这就要求我们在教学中做到心中要有学生,不怕学生的“打扰”.虽然上述解法中不乏“杀鸡用牛刀”的现象,却都是学生难得的思想火花.况且我们解题的目的并不是为了纯粹地解题,而是通过问题发现问题,其目的往小了说是提升学生的数学素养,往大了说就有可能推动数学学科的整体发展,数学史上无数次的“猜想”无不在验证着这一点.另外在教学过程中应该努力提高学生的问题意识和提问技能,要鼓励学生提出问题,平等地与学生探讨问题的解决方案.

要提高解决问题的能力,就应该在教学过程中渗透数学文化[4].比如学生之所以能巧妙地想到解法4,就是因为他们善于利用“阿氏圆”解决“胡不归”问题.在数学教学的课堂上,“习题、公式、定理”不应该是课堂的唯一形式,我们可以通过“作者介绍”使学生了解数学知识的来龙去脉以及赖以生长的“土壤”,以丰富学生对数学知识的感性认识;也可以来一段“数学家逸事”使数学知识折射出人的意志和智慧,使学生在感动之余能更好地掌握数学知识;更可以通过解读“数学作品”让学生感知数学的和谐美、理性美．总之,数学教学课堂上应该有一些“非数学”的内容,让学生的思维不受局限!

要提高解决问题的能力,就应该有优化自身知识结构的意识[5].在教授高中知识的同时,应该有意识地加强大学的高等数学相关知识,甚至是初中和小学相关基础知识的吸收．比如学生之所以能想到解法3,就是因为没有拘泥于解斜三角形的正弦定理和余弦定理,而是通过构造直角三角形,用初中的勾股定理解决;再比如解法4的思想源泉——“阿氏圆”与“胡不归”,就是出自初中最值问题的一个经典模型,这些解法优势可谓明显.学生能喝上的这“一碗水”,很大程度上就源于教师身上那“一桶水”甚至是“常流水”.而教师身上之所以能拥有“一桶水”或者“常流水”,是因为他能不断地审视自身的专业知识,了解其与当前专业要求的差距,进而订立业务进修计划,拓宽、夯实、弥补专业基础,最终不断优化自身知识的结构,为提高学生解决问题的能力、提升数学核心素养保驾护航.