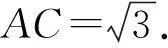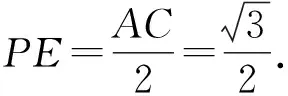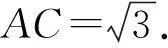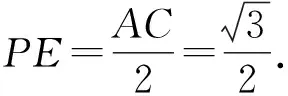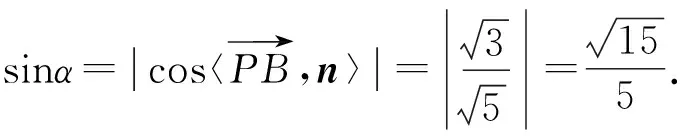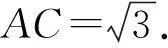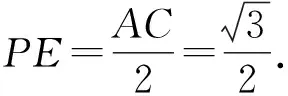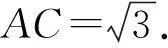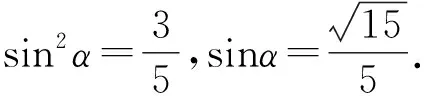对2022年一道立体几何题多种解法的研究
刘大鹏
(辽宁省黑山县第一高级中学,辽宁 锦州 121400)
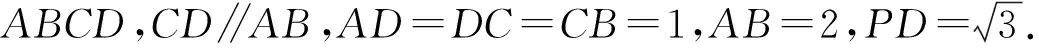
(1)求证:BD⊥PA;
(2)求PD与平面PAB所成角的正弦值.
1 解法展示
1.1 第(1)问解析

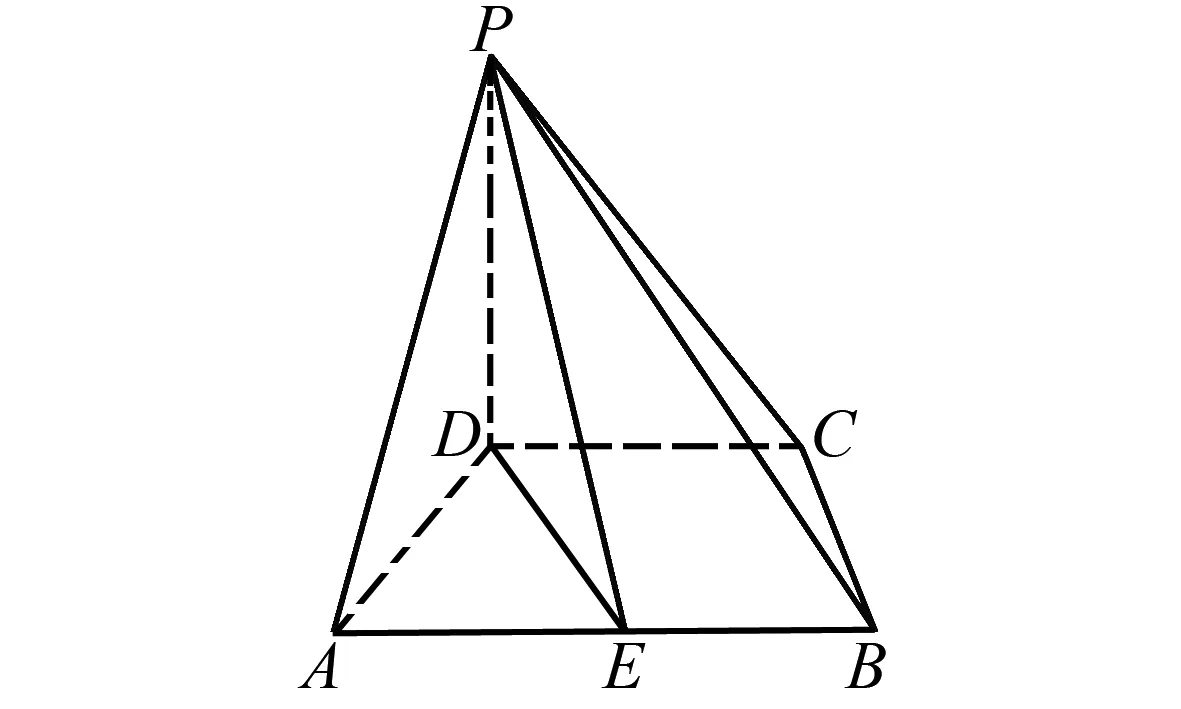
图1 2022年全国甲卷18题
因为AD2+BD2=AB2,所以BD⊥AD.
又因为PD⊥面ABCD,BD⊂面ABCD,所以BD⊥PD,AD∩PD=D,所以BD⊥面PAD,PA⊂面PAD,所以BD⊥PA.

评注解法2用到了托勒密定理(圆的内接凸四边形两组对边乘积的和等于对角线的乘积),解法新颖,对拓宽学生的知识面及培养学生的发散思维能力都大有裨益.
1.2 第(2)问解析

在△DAE中,
DE2=1+x2-x,


解法2 (定义法)如图2,过点D作DF⊥AB于点F,连接PF,由PD⊥面ABCD,AB⊂面ABC,所以PD⊥AB.因为PD∩DF=D,所以AB⊥面PDF.
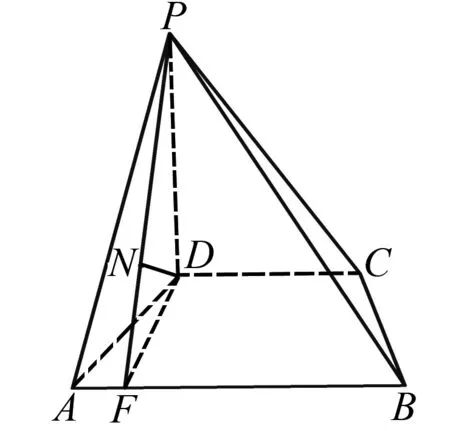
图2 定义法图
因为AB⊂面PAB,所以面PDF⊥面PAB.
过点D作DN⊥PF于点N,则DN⊥面PAB.
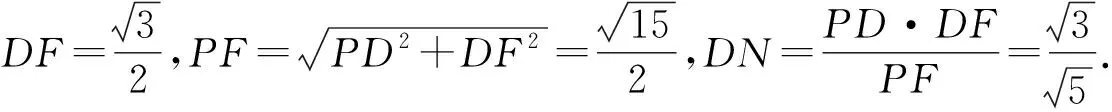

评注求点D到面PAB的距离,可以用等积法(即VP-ABD=VD-PAB),从而不必作辅助线.

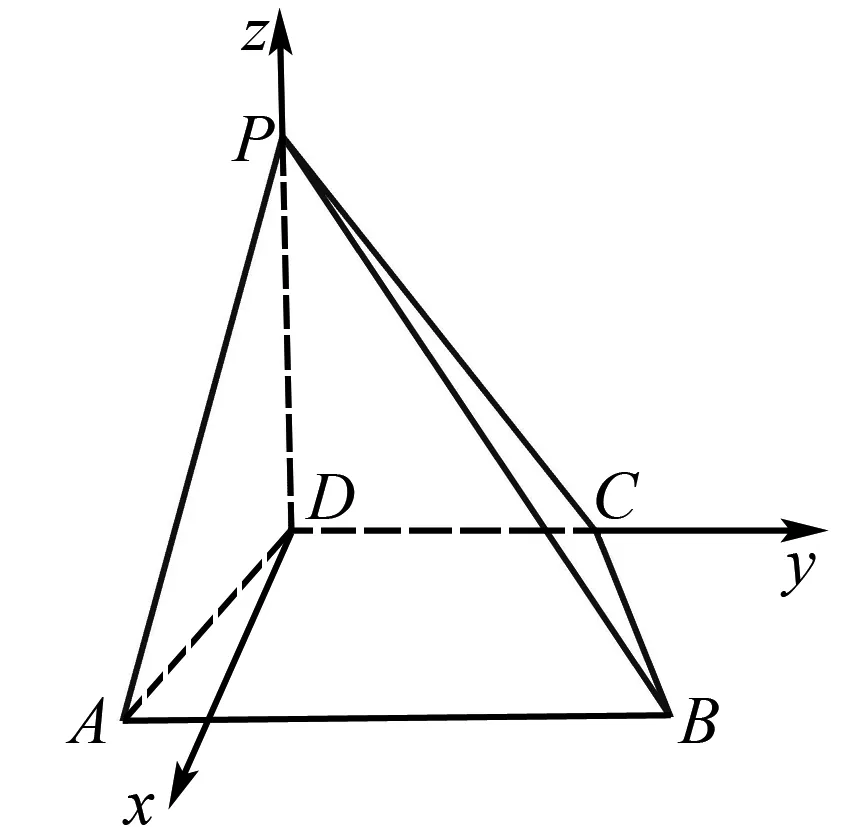
图3 向量法图

n=(2,0,1)是面PAB的一个法向量.

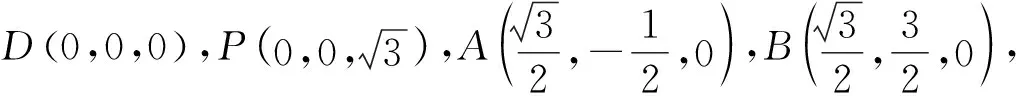
评注本解法用到了平面的点法式方程A(x-x0)+B(y-y0)+C(z-z0)=0,其中n=(A,B,C)是平面的一个法向量,P(x0,y0,z0)是平面上的一个定点,用到了点M(x0,y0,z0)到面α:Ax+By+Cz+D=0的距离公式
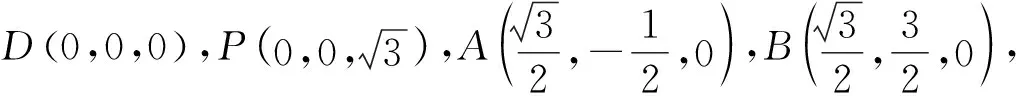


记直线PD与面PAB所成角为α,则
评注本解法建立了二元函数解析式,并用权方和不等式求出了函数最大值.
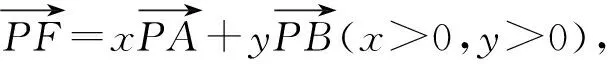

记直线PD与面PAB所成角为α,则


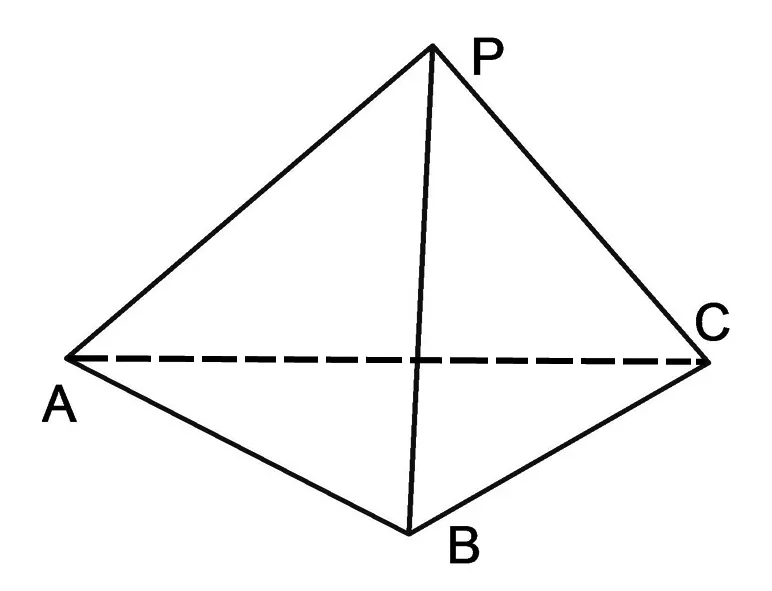
图4 三面角图
我们把它称为三面角公式1.用它求二面角不需要作辅助线,非常方便,能提高解题速度.
解法7 由解法2知,PD和它在面PAB上的射影都与AB垂直,过点P作PE∥AB,则PD与面PAB所成的角等于二面角D-PE-A的值.


2 变式训练题及解法研究
变式在四棱锥P-ABCD中,底面ABCD是梯形,AD∥BC,AD=2BC,PA⊥PD,AB=PB=1,
(1)求证:PA⊥平面PCD;
(2)若BC=CD=1,当四棱锥P-ABCD的体积最大时,求直线PB与平面PAD所成角的正弦值.
本文只研究第(2)问的解法.
解法1 (利用最小角定理)由(1)得AP⊥PC.如图5,取AC中点E,连接PE,四边形ABCD是等腰梯形.

图5 利用最小角定理解析
所以AC·BD=AC2=AB·CD+AD·BC=3.
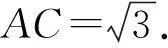
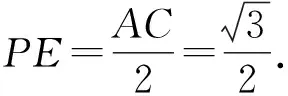
当PE⊥面ABC时,VP-ABCD有最大值,此时



令t=3-x(1 记直线PB与面PAD所成角为α,则 α=(∠BPF)min, 解法2 (定义法)由(1)得AP⊥PC,取AC中点E,连接PE,四边形ABCD是等腰梯形, 所以AC·BD=AC2=AB·CD+AD·BC=3. 当PE⊥面ABC时,VP-ABCD有最大值,此时 记B到面PAD的距离为h,由VP-ABD=VB-PAD, 所以AB·BD·PE=PA·PD·h. 记直线PB与面PAD所成角为α,则 解法3 (向量法)由(1)得AP⊥PC,取AC中点E,连接PE,四边形ABCD是等腰梯形, 所以AC·BD=AC2=AB·CD+AD·BC=3. 图6 向量法解析图 解法4 (向量法)由(1)得AP⊥PC,取AC中点E,连接PE,四边形ABCD是等腰梯形, 所以AC·BD=AC2=AB·CD+AD·BC=3. 记B到面PAD的距离为h,则 解法6 (向量法+最小角定理)由(1)得AP⊥PC,取AC中点E,连接PE,四边形ABCD是等腰梯形,所以AC·BD=AC2=AB·CD+AD·BC=3. 当PE⊥面ABC时,VP-ABCD有最大值,