异构多无人机中的任务分配优化问题
牛 源,崔志华,白 慧
(太原科技大学 计算机科学与技术学院,太原 030024)
1 引 言
无人驾驶飞机简称无人机(UAV),它具有体积小,价格低,以及战场生存能力强等优点.随着时代的发展,人们常常会在商业宣传、娱乐航拍、农业灌溉等民用领域见到它,除此之外,在治安维护、紧急救援、空中侦查等军事行动也有无人机的身影,因此,无人机在很多国家的重要作用越来越显著[1].异构多无人机任务分配是指将不同类型无人机组合在一起,按照规定执行需要完成的任务,同时对每架执行任务的无人机规划其相应飞行路线[2].但是,面对日益复杂的任务环境和任务类型,单个无人机已经无法同时完成对多个目标的侦查、攻击和评估任务的要求,与此同时,大部分的作战任务都需要不同类型的多架无人机一起完成任务.相应地,在满足无人机约束条件下,从任务完成角度确定出多目标最优值,充分发挥异构多无人机整体完成任务的能力.因此异构多无人机任务分配成为了未来研究的趋势.
异构多无人机任务分配作为关键技术,已经引起学术界和科学家的极大的兴趣,他们十分关注和积极研究,积累了大量算法并已取得一定的成果,主要有:数学规划方法、群算法和智能优化算法.数学规划方法是运筹学的一个重要分支,通常都具有较高的时间和空间复杂度,如线性规划、动态规划和分支界定法都是利用问题具体特征来获得求解.然而,异构多无人机多任务分配模型往往比较复杂,约束多,难以找到显著特征找到解.群算法是一种新兴的演化算法,其中蚁群算法[3]、粒子群算法[4]、以及鱼群算法[5]是最为典型的群算法.苏菲等人[6]提出分工机制的蚁群算法,根据任务分配的特点,设计了基于任务能力评估的问题解构造策略和基于任务代价的状态转移规则,提高了算法的性能.Yan等人[7]主要研究海上任务分配,在智能船舶控制系统仿真的基础上,用粒子群算法实现任务分配的路径规划.Zhou等人[8]主要研究算法收敛性,将粒子群和鱼群算法混合优化,充分说明算法在后期出现搜索能力不够、收敛速度慢问题.智能优化算法是通用性强且适合并行处理的算法,适合求解大规模问题,其中遗传算法[9]、灰狼算法[10]和模拟退火算法[11]等是典型的优化算法.Yu等人[12]主要研究自适应遗传算法中无人机分配问题,将任务分配问题从数学上抽象为一个模型进行求解.向庭立[13]等人对兴趣区域进行覆盖探测的任务分配,通过最小圆覆盖法确定无人机在兴趣区域中的目标航迹点,其次在目标分配模型的基础上建立时间分配模型,然后利用灰狼算法对任务分配模型进行求解.但是这只是以时间成本作为目标,比较单一化.智能优化算法可以解决单目标、多目标和高维多目标问题,目标越多约束和求解过程越复杂.单目标优化算法最常用,很多研究者碰见多目标问题,也喜欢将其不同目标赋予一定权重,根据权重求和,将多目标问题间接转化为单目标问题.显然单目标优化算法求解简单化了问题,实验结果也在接受范围,但是这种做法缺点显而易见.首先,目标参数很难确定,决策者主观性较强.其次,单目标最优解通常是全局唯一最大或者最小解,而多目标存在有的目标解优于或者劣于其他解,提供的是一组较优解.最后,多目标加权在实验部分,只有通过不同加权组合丰富实验,弥补实验的不足,但是很多次的组合实验时间花费较大,而且每次实验之间无法比较,导致决策者很难做出有效的决策.
NSGA-II是典型的多目标算法,实验结果证明优于有代表性的其他几种算法.但是在解决一些问题仍有不足,刘旭红等人[14]提出累积排序适应度赋值策略,能同时考虑个体的Pareto排序值和密度信息,提高了算法的搜索性能.张永娇等人[15]对交叉算子引入的参数α与每个个体所在群体中的等级有关,根据参数α使前一代较优个体在后一代尽可能保留下来,具有更好的全局搜索能力.王珑等人[16]在风力机叶片的优化研究中,提出一种采用精英控制策略和动态拥挤方法,具有很好的收敛速度.当前对于NSGA-II算法的改进研究较为丰富,但大部分都是决策者根据偏好来改进,涉及很多目标时要综合衡量.
本文在多无人机和多目标位置随机情况下,以异构多无人机对多目标同时进行侦查、打击和评估任务为背景,在满足多种约束前提下,建立总体完成时间、攻击收益和路径成本为目标函数的多目标模型.针对多约束多目标特征采用多个不同类型基因对多目标进行编码,整数编码中的单点交叉和位突变,解的收敛较快,容易陷入局部最优,为解决此问题,采用混合变异策略改进多目标遗传算法(I-NSGA2)进行求解,提高解的均匀分布性.最后,通过仿真实验证明算法和模型有效性.
2 异构多无人机任务分配模型
2.1 任务场景描述
设有L架无人机组成异构无人机组U={U1,U2,…,UL},对M个目标T={T1,T2,…,TM}分别依次进行侦查(classify,C)、攻击(attack,A)和评估(verify,V)任务,其中L>M.关于任务需要满足两个约束:1)每个目标点都完成C、A、V时,才完成所有任务,总共需要执行的任务总数为Nc=3M;2)C、A、V任务执行顺序遵循严格的任务优先级约束.任务A只能在执行侦查C目标分类后执行,任务V只能在完成任务A后执行.
不同类型的无人机对于功能不同,将无人机分为侦察无人机(R)、攻击无人机(H)和全能无人机(ALL)3种类型.这些无人机任务类型分别为:1)侦察机:侦查C、评估V;2)攻击机:攻击A;3)全能机:侦查C、攻击A、评估V.异构无人机性质不同,不同无人机有不同运动学参数[17],包括不同的运动速度[V1,V2,…,VM].除此之外,有不同的打击收益[P1,P2,…,PM].作战示意图如图1所示.
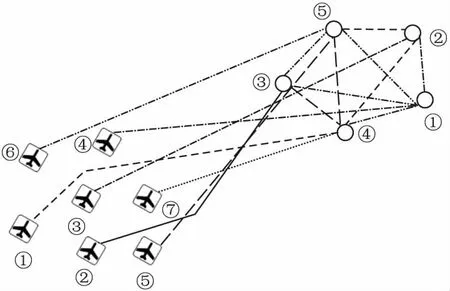
图1 作战示意图
2.2 约束条件
异构多无人机在对多个目标点都进行侦查、打击和评估任务时是一个多目标多约束的问题,其中,主要是任务完成数量约束、任务时间顺序约束、无人机资源约束、无人机协同约束、携带打击弹药约束:
1)任务完成数量约束:保证所有目标点分别都执行了C、A、V 3类任务,可表示为:
(1)
式(1)中:k=1,2,3分别对应于 C,A,V.
2)任务时间顺序约束:对所有目标点执行任务时,先侦查,后打击最后评估,可表示为:
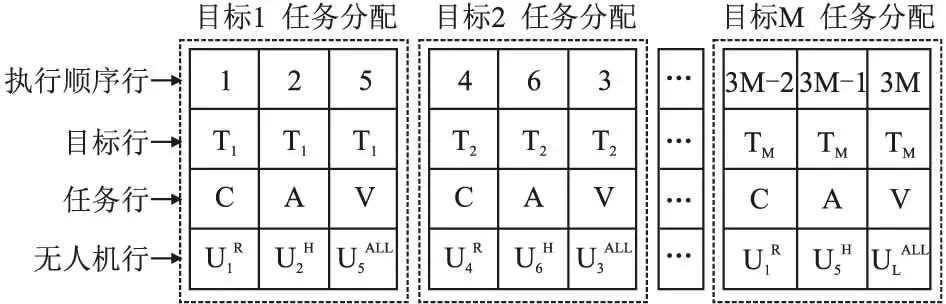
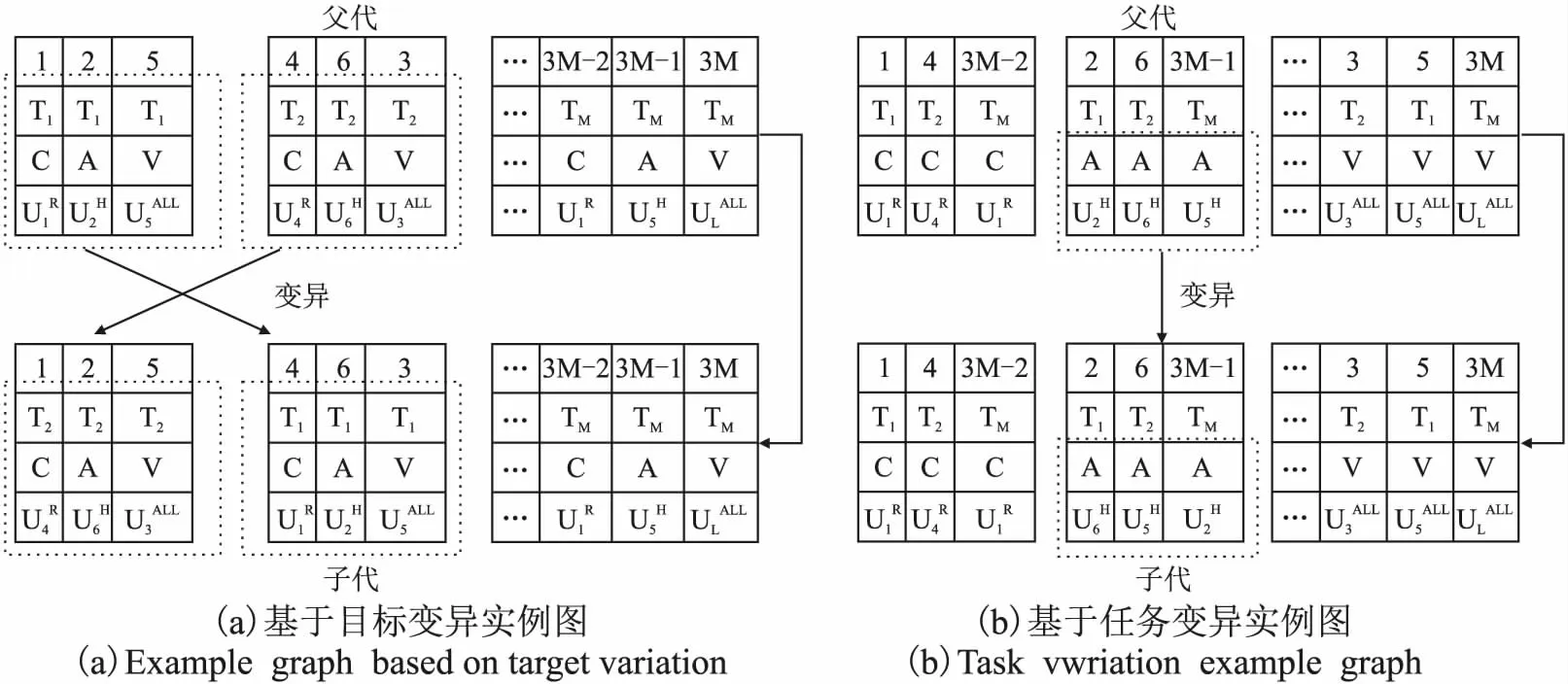
tiC (2) 式(2)中,tiq(i=1,2,…,L;q=C、A、V)表示为目标i被无人机执行相应任务的时间. 3)无人机资源约束:所有目标点相应任务对应相应无人机类型执行,可表示为: (3) UH=A 打击 (4) (5) 式(3)~式(5)中:Uq1(q1=R、H、ALL)表示不同类型的无人机. 4)多无人机协同约束:所有目标点的任务都只能被完成一次,即无人机多同一目标点只进行一次侦查、打击和评估,可表示为: (6) 式(6)中,Ni表示第i架无人机执行任务数. 5)携带打击弹药约束:无人机必须在携带充足弹药下对目标点执行打击任务,即无人机攻击的目标数必须小于等于最大弹药数,可表示为: (7) 式(7)中,mu表示执行攻击类型无人机弹药数. 此类问题通常会选取航行时间作为分配方案重要标准,本文是异构多无人机任务分配为背景,根据所有目标点的任务被完成后无人机总路径成本、总体完成时间和攻击收益作为多目标作衡量标准.以下是目标函数: 1)总路径成本:无人机在任务分配时,由于能耗有限,尽可能希望路径长度最短,所以总路径成本指的是所有无人机到完成任务的目标点的距离总和,建模表示如下: (8) 其中,L是无人机数量,M个目标点,dij是第i架无人机到第j个目标点的欧几里得的距离. 2)总体完成时间代价:由于不同类型无人机执行任务速度不同,所以时间代价是由路径消耗时间和执行任务时间两部分组成,建模表示如下: (9) (10) T2=Δnl×Δt (11) 式(9)中,T1是路径上消耗时间,T2是执行任务时间.式(10)中,Dl是第l架无人机路径和,Vl是第l架无人机对应运动学速度.式(11)中,Δnl是第l架无人机执行任务总数,Δt是执行任务时间,取值5S.T为所有无人机完成任务的时间代价. 3)攻击收益:不同类型的无人机打击收益效果不同,即尽可能使用攻击效果好的无人机执行任务,使得收益最大化,建模表示如下: (12) 式(12)中,Pij表示第i架无人机在第j个目标点攻击概率,Wij表示第i架无人机在第j个目标点攻击收益. 传统任务分配算法主要解决特定问题下的单目标优化问题,无法适应多需求的战场环境.而多目标算法可以为决策者提供更适合现实情况解决方案.在实际生活中,人们往往会遇到各种优化问题,一般来说,这些优化问题会被分为单目标优化和多目标优化.单目标优化问题:只优化一个目标函数,仅有唯一最优解.多目标优化问题:目标函数有两个及以上(n<=3),各个目标之间是非线性或者冲突的,即一个目标的改善通常会导致至少一个其它目标的退化.而当目标个数超过3,就称为高维多目标优化[17]问题.数学描述为: minF(x)=[f1(x),f2(x),…,fm(x)]T (13) s.tgi(x)≤0,i=1,2,…,p (14) NSGA-II由K-Deb教授于2002年提出.它是NSGA的改进,NSGA-II使用改进的快速非支配排序,时间复杂度由O(MN3)降低为O(MN2),同时采用了一种精英策略,不仅可以将父代的优秀个体直接保留在父代中,而且还可以防止丢失所获得的帕累托最优解,从而提高了搜索性能.NSGA-II通过使用了拥挤度距离来衡量解决方案的分布性和多样性,从而改善参数共享策略在这些方面的不足. 异构无人机任务分配是多约束多目标问题,由多类型基因整数编码组成的染色体,仅用单点交叉和位突变,根据迭代次数收敛过快,容易陷入局部最优.针对此问题并结合异构无人机任务分配问题特征,采用改进I-NSGA2算法,提高解的分布性. 3.3.1 个体编码 假设来自同一组L架多无人机,在M个目标上执行任务,可行的编码示意图如图2所示.本文对于异构多无人机任务分配问题,我们采用基于目标多类型基因整数编码原则,如图3所示. 图2 编码示意图 图3 基于目标多类型基因整数编码 在图2中,个体由Mm×Nc矩阵组成,其中,Mm表示位,包含4个元素,依次为:执行顺序行、目标行、任务行和无人机行.执行任务顺序行是Nc个任务被执行顺序;目标行是Nc个目标;任务行是M个目标点任务类型;无人机行是针对第M个目标点执行任务类型匹配的无人机.Nc=3M表示3种类型U=(UR,UH,UALL),UR侦察类型无人机、UH攻击类型无人机和UALL全能类型无人机.个体中的每一列描述了某种无人机的配置,即表示将针对某个目标的某个任务指派给某个无人机来执行. 从图3中我们可以看到,染色体由4×3M矩阵组成,每一列中基因位都是整数表示,每一列基因代表完成一个任务.对于每个目标点都需要执行3次任务,如果对其执行打击(UH)任务或者评估(UALL)任务无人机比侦察(UR)任务无人机先到达目标点,则UH和UALL必须等到UR执行完才可以攻击和评估.那任务顺序是混乱的且时间会延迟,为了避免该情况发生,在图2基础上加以改进,将任务时序引入编码中,将同一目标的按照执行任务顺序从侦查、打击到评估的排列规则生成基于目标多类型的染色体.基于目标多类型整数编码满足约束条件.首先,每个基因分配的无人机行具有任务行所需的相应能力.然后,从任务C、A、V的执行顺序中可以看出,它们不仅都被执行,而且每个目标都按顺序执行.因此,基于多类型基因整数编码满足第2.2节中所述的约束条件. 3.3.2 快速非支配排序和拥挤度距离 异构多无人机任务分配优化问题的优化目标就是要找到成本最小收益最大的分配方案.快速非支配排序是减少搜索复杂度,将种群中所有个体遍历,存入到所有非支配集合中rank.拥挤度距离表示在种群中给定点周围个体分布情况,用id表示,即反映种群多样性,直观上用个体i周围,但不包含其他个体的最大长方形表示. (15) 3.3.3 交叉 交叉操作一般起全局搜索的作用,可以开采未知的空间,有助于将优良个体的染色体片段遗传给后代,本文采用分段交叉,交叉方式如下: 假设两条父代的染色体分别为p1和p2,其中: 1)p1为种群前一半,p2为种群后一半.随机初始化交叉点的位置和交叉长度. 2)分别找出p1和p2的交叉段,将p1的交叉段插入p2的交叉点中,p2操作同p1一样. 3)交叉得到新的子代s1和s2.将s1和s2合并.如图4所示. 图4 交叉实例图 3.3.4 变异 变异操作是为了增加种群的多样性,本文是整数编码,对个体编码串中以变异概率、随机指定的某一位或某几位仅因位上的值做变异运算.变异概率一般在5%以下.本文采用混合变异策略,基于目标变异和基于任务变异.采用如下变异操作: 基于目标变异,设染色体的编码为4×3M矩阵,其中: 1)按照目标顺序排列,随机生成正整数r1和r2,且r1,r2均小于等于M. 2)交换染色体中r1和r2目标点对应的目标行、任务行和无人机行基因.如图5(a)所示. 图5 基于任务变异,设染色体的编码为4×3M矩阵,其中: 1)按照任务顺序排列,随机生成正整数r2,且1≤r2≤3. 2)交换染色体中r2任务对应的目标行、任务行和无人机行基因.如图5(b)所示. 在异构多无人机中采用NSGA-II算法进行任务分配时,由于多类型基因整数编码方式,在整数交叉变异时仅采用单点交叉和位突变,存在容易陷入局部最优,多样性不好的情况,所以本文中对NSGA-II算法进行改进,用基于目标和任务两种变异策略(I-NSGA2)增加种群多样性,使算法求解更均匀和满足最优任务分配.具体算法步骤如下: Step1.输入无人机数L、目标点数M、无人机集群点和目标点集群坐标点U(x,y,z)、TM(x,y,z)等变量. Step2.创建一个4×3M全零矩阵染色体,4×3M×50细胞组定义种群.基于目标多类型基因整数编码,随机产生初始种群. Step3.非支配排序和拥挤度距离,生成第一子代种群; Step4.迭代开始,选择、交叉、变异,其中后2/3代中,前一半种群进行基于目标变异,后一半种群进行基于任务变异.期间,满足公式(1)~公式(7)约束. Step5.快速非支配排序和公式(15)计算拥挤度距离, Step6.重复Step 4~Step 5直到可以停止算法的最大迭代次数. Step7.根据公式(8)~公式(12)计算适应度值,完成最大的迭代次数,计算目标值并找到最优任务分配方案. 总的算法流程图如图6所示. 图6 算法流程图 为了验证算法和模型的有效性,我们设置了无人机集群和目标点集群在指定范围内随机位置生成实验场景,本文中无人机数为7架,目标点为5个,对于整个异构无人机中任务分配问题设计到无人机参数、目标点参数和任务时间窗参数分别如表1、表2和表3所示,本实验在处理器为Intel(R)Core(TM)i5-8250U CPU @ 1.60GHz 1.80 GHz,Win10 64位操作系统,4GB RAM环境下对I-NSGA2算法进行仿真.用于仿真的软件是MATLAB®R2019b. 表1 无人机基本信息 表2 目标基本信息 表3 任务时间窗 无人机集群起点和目标点分别在三维空间的某个区域,表示三维大气中的坐标点,其中,坐标轴范围为(0,500m,500m),无人机集群随机生成范围为(0m,200m,200m),目标点随机生成范围为[(200m,500m),(200m,500m),(200m,500m)].采用对比法,与典型多目标GrEA算法[18]、KnEA算法[19]、RVEA算法[20]和 NSGA-II算法[21]分别在同一场景下进行比较.此外,在进化多目标优化算法的 MATLAB 平台,本文的I-NSGA2与已改进的多目标r-NSGA-II算法[22]、g-NSGA-II算法[23]、NSGA-II-conflict算法[24]和RPDNSGA-II算法[25]作对比试验,证明I- NSGA2算法在解决异构无人机任务分配问题的有效性. 图7显示了代数和各目标值收敛情况图,每组实验不同代数均跑10次实验,求取平均值.图7(a)是总路径成本和代数收敛情况图,图7(b)是总时间代价和代数收敛情况图,图7(c)是攻击收益代数和收敛情况图.由图7(a)~图7(c)我们已经清楚地看到,随着迭代次数的增加,各个目标值逐渐减小.在150代后有个明显目标值变化,在200代后开始收敛,甚至趋于稳定,表明各目标在已经有最优值. 图7 代数和各目标收敛情况图 图8是I-NSGA2和GrEA、KnEA 、RvEA、NSGA-II这4种不同多目标算法的对比结果图,通过箱盒图可以直观看出,在算法收敛时,各目标值对比情况.图8(a)是总路径成本算法对比图,图8(c)是攻击收益算法对比图,在相同情况下,我们的I-NSGA2算法在处理异构多无人机任务分配问题时,总路径成本和攻击收益性能两个指标上算法优化结果中的中位线都有明显提升,在路径花费少时,攻击收益大.同时其优化结果中的最优值相较于其余4个算法表现优异.图8(b)是总时间代价算法对比图,I- NSGA2最小值和中位线优于其他4个算法,且无任何异常点.混合变异算法在算法后期注重解的多样性,因此,在总路程成本代价以及攻击收益指标上可以看出算法优化的多样性相较于其余4个算法更优,同时对比算法优化产生的最优值可以看出改进算法在5个目标上的收敛性更优.由于多目标优化算法优化产生的解为Pareto解集,因此产生的解必定不可能在多个目标上同时表现最优,决策者可根据实际需求选取符合其需求的解. 图8 不同多算法对比结果图 图9是I-NSGA2和r-NSGA-II、g-NSGA-II、NSGA-II-conflict、RPDNSGA-II在MATLAB多目标优化算法平台,对已有NSGA-II做出改进算法的对比结果图,通过箱盒图可以清楚看出,在算法收敛时,各目标值对比情况.图9(a)是总路径成本算法对比图,图9(b)是总时间代价算法对比图,图9(c)是攻击收益算法对比图.I-NSGA2在3个目标值上,无任何异常点,此外,不论是中位线还是最大最小值都优于其他4类算法.说明I-NSGA2算法经过迭代优化后,在解决异构无人机任务分配问题上效果好鲁棒性强.r-NSGA-II和g-NSGA-II算法是决策者偏好的改进,而本文的改进是综合考虑多目标多约束问题,更能获得综合性好的解.对比NSGA-II-conflict算法,本文的多目标函数有两两冲突,也有相互无关,针对仅对冲突多目标的改进,I-NSGA2在总路径成本和时间代价上都优于NSGA-II-conflict算法.RPDNSGA-II算法在非主导解集上创建一个严格的部分顺序,而I-NSGA2采用非支配排序,并结合异构无人机任务分配多基因整数编码方式特点,使用混合变异策略,不仅可以保留Pareto前沿解,还可以增加解的多样性. 图9 已改进NSGA-II算法对比结果图 采用改进NSGA-II算法(I-NSGA2)的任务分配方案,得到的仿真结果如图10~图12所示.3种不同类型的7架无人机,按照任务完成数量、多无人机协同等多约束完成对随机分配的5个目标点侦查、打击和评估任务,并在短时间内获得最大攻击收益,而且不会出现顺序混乱情况.图10是各目标点被侦查、攻击和评估结果,可以清楚看出,各目标点任务均被执行且按照执行顺序完成.图11是异构多无人机任务分配方案,由图可以看出无人机群协同都执行各自匹配类型任务.图12给出异构多无人机任务分配三维路径轨迹图,每个无人机在优化算法结果下,按照分配方案规划飞行轨迹. 图10 各目标点被侦查、攻击和评估结果 图11 异构多无人机任务分配方案 图12 异构多无人机任务分配路径轨迹图 除此之外,由优化结果可以得到异构多无人机任务分配优化问题中需要的最大路径长度是5006.86m,最久执行任务时间是56.57s,最大攻击收益是2811.6. 以针对目标4的侦查、评估和打击为例,说明异构多无人机任务分配和路径规划情况.根据图10和图11可以看出目标4的3个任务被U1、U6和U2协同完成.U6必须在U1对目标4执行完侦查后才能打击,同样的U2必须在U6后才能评估.U1除了在目标4 执行任务,对T1和T3也有任务,但是由结果图可知在时间上并不冲突.多无人机对其他目标的任务执行情况可类似分析. 本文针对异构多无人机静止地面多目标上执行敌方防空的抑制任务分配优化问题,建立以总路径距离、总时间代价和攻击收益的多目标模型.同时,对NSGA-II算法进行改进,在算法中将任务时序引入编码,避免了时间延迟情况,并且采用混合变异策略,以提高最优解的均匀分布性.仿真实验证明了模型的合理性和算法的有效性. 在未来的工作中,可以将无人机的损失、通信传输等因素考虑,但是随着目标和约束增加,利用多目标算法将大大降低,此时,高维多目标算法可以很好解决此类问题.2.3 目标函数
3 改进的NSGA-II算法
3.1 多目标优化算法
3.2 NSGA-II算法
3.3 NAGA-II算法的改进(I-NSGA2)

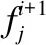

3.4 算法流程
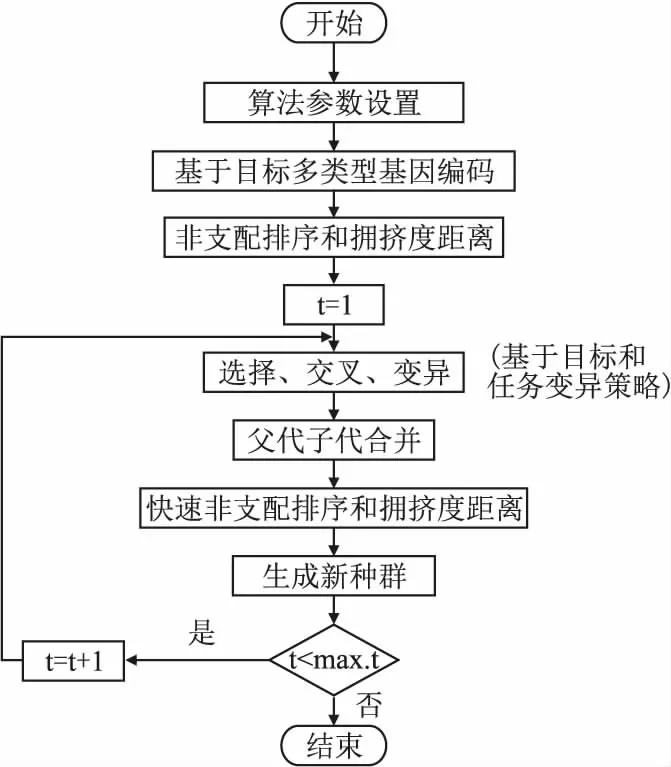
4 仿真实验及结果分析
4.1 场景和参数设置



4.2 实验结果
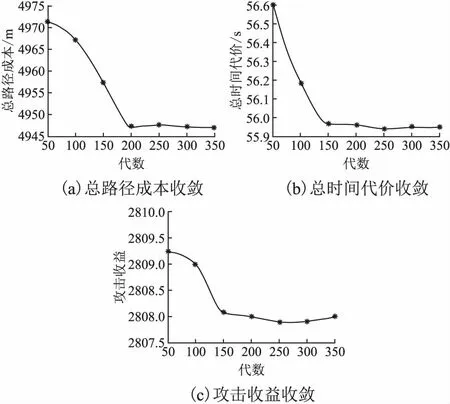


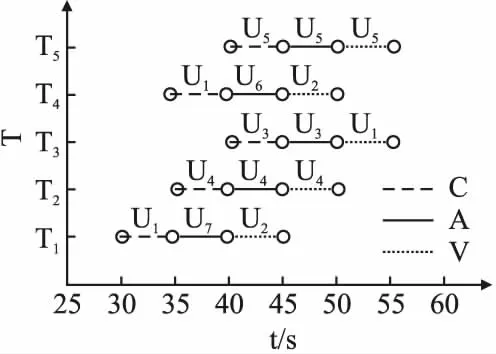


5 结 论

