度量学习引导的加权聚类集成算法

吴建国,魏 巍,2,郭鑫垚,闫 京

1(山西大学 计算机与信息技术学院,太原 030006)

2(山西大学 计算智能与中文信息处理教育部重点实验室,太原 030006)

1 引 言

聚类分析是机器学习中一种典型的无监督算法[1],聚类算法依据相似性原理将一组数据对象划分为一定数量的同质组(簇),使得同簇内数据对象有较高的相似度,不同簇内数据对象相似度较低.聚类分析也是文本挖掘[2,3]、社区发现[4-6]、推荐系统[7,8]以及图像处理[9,10]的核心技术.聚类概念被提出几十年以来,涌现出了大量的聚类算法[11].然而,这些聚类算法普遍存在一些不足,如不同的聚类算法具有不同的目标函数,导致其只能处理特定的数据结构和特定形状的聚类;一些聚类算法高度依赖于初始化参数,如K-means算法等.为解决以上单一聚类算法的各种不足,同时为应对单一的聚类算法无法有效处理当前多样化数据类型和复杂数据分布的挑战,研究人员将集成学习技术应用于聚类分析算法,提出了聚类集成的概念.

聚类集成又可称为聚类融合,其算法的思想为使用不同的聚类算法,或同一聚类算法设置不同初始化参数得到基聚类集合.在此基础上,对基聚类结果使用组合策略进行集成,获得最终聚类集成结果,以此提升聚类算法的聚类准确性和鲁棒性[12].然而,传统聚类集成方法无法自动的评估基聚类的质量,等权重的考虑每个基聚类,容易受到低质量基聚类的影响.为减轻低质量基聚类对聚类集成结果的影响,通常根据基聚类的质量好坏赋予其不同的权重,质量较好的基聚类赋予较高权重,反之较低.Berikov等人[13]在理论上证明了加权聚类集成算法的必要性.在一定的假设情况下,任意一对样本被错分的概率随着聚类集成规模的加大而趋于收敛,因此在时间以及存储有限的情况下,聚类集成规模较小时,对基聚类进行加权是非常有必要的.Li等人[14]将聚类集成问题转化为非负矩阵分解的问题,提出了一种非负矩阵加权的聚类集成算法,在非负矩阵分解的过程中为每个基聚类赋予不同的权重.Xue等人[15]提出了一种基于地标点的谱聚类算法,首先使用该算法生成基聚类集合,然后以信息熵为依据计算各基聚类的不确定性,并根据不确定性的大小确定基聚类的权重.Huang等人[16]提出了一种基于局部加权的聚类集成算法,采用熵准则评估基聚类中各个簇的不确定性,依据该不确定性进行共协关系矩阵的局部加权,并基于此共协关系矩阵分别采用层次聚类算法及图分割算法得到聚类集成结果.Xu等人[17]将簇的可靠性评估转化为粗糙集中的不确定性度量问题,同时设计了一种样本局部相似性度量方法,将这两种度量方法用于对共协关系矩阵的加权,并基于此共协关系矩阵求得聚类集成结果.

虽然上述加权聚类集成方法能够很好的从不同层次评估其质量并赋予其不同的权重,但该类方法往往基于欧氏距离,而欧式距离对数据的所有特征等权重考虑.相比之下,马氏距离考虑数据特征之间相关性以及差异性,可以更好的刻画样本之间的相似性.因此,本文受马氏距离度量学习的启发,提出了一种度量学习引导的加权聚类集成算法(WEC-ML),该方法在学习样本间的马氏距离度量的同时,考虑每个基聚类结果中样本对的划分,将大多数基聚类结果认为相似的样本对拉近,将基聚类结果认为不相似的样本对推远.通过以上过程,求得新的马氏距离度量,在新的投影空间中赋予各个基聚类新的权重.进一步,本文将马氏距离度量学习与基聚类权重学习相融合,相互指导,在不断迭代中求得最优权重,从而提升聚类集成算法性能.

本文主要贡献总结如下:

1)提出了一种度量学习引导的加权聚类集成算法.算法在每次迭代中学习不同基聚类的权重并进行聚类集成,基于集成结果构建成对约束,学习新的马氏距离度量,将划分为同簇的样本拉近,不同簇的样本推远,并在新的投影空间中为基聚类结果学习新的权重.

2)将马氏距离度量学习与基聚类权重学习整合到同一个优化问题中,实现了二者的相互指导.

3)在12个真实数据集上的实验结果表明,聚类集成效果有明显提升,表明马氏距离度量学习对于基聚类加权的有效性.

2 相关工作

2.1 度量学习

度量学习利用样本标签信息生成约束,将同类样本之间的距离拉近,不同类样本之间的距离推远,学到一个更加准确刻画样本之间的相似性度量[18].广泛来说,可认为度量学习学习到了一个特征表示空间,在该空间中样本之间的距离度量能反映出数据的特性.距离度量对许多机器学习方法性能具有重要的作用,如经典聚类方法K-means涉及到样本之间距离的计算,学习合适的距离度量可以有效的提升聚类性能.传统欧式距离假设数据不同的特征重要性相同,并且数据特征相互独立.然而这种假设在真实场景中一般是不成立的,因此往往需要使用更加通用的马氏距离[19]度量样本对之间的相似性.马氏距离度量的定义如下:

(1)

其中,M反映了样本特征之间的关联性以及样本特征的权重.M为半正定矩阵,当M为单位矩阵时,马氏距离会退化为欧式距离.

2.2 聚类集成

聚类集成是指给定一个基聚类集合,通过对该基聚类集合进行融合以获取数据的团簇结构,从而得到相比于现有聚类结果更加鲁棒、更加稳健的聚类集成结果[20].与传统聚类方法相比,聚类集成算法更具有普遍性、准确性和鲁棒性.因此,聚类集成算法得到广泛的研究与应用.聚类集成过程通常分为两个步骤,分别为基聚类生成和一致性函数的设计[21].常用的基聚类生成方法有:同一聚类算法使用不同的初始化参数(不同的初始状态),如K-means算法设置不同的初始簇中心点;同一数据集,使用不同的聚类算法[22];同一算法在不同数据集的子集进行聚类[23];通过聚类评价指标挑选基聚类[24].采用不同的基聚类生成方法生成基聚类集合后,需将其转化为统一的、综合的聚类结果,即一致性函数的设计.根据一致性函数设计方法的不同,现有聚类集成算法可分为:基于共协关系矩阵的聚类集成算法、基于图划分的聚类集成算法等.

基于共协关系矩阵的聚类集成算法通过统计两个样本在多个基聚类结果中出现在同一簇的次数构建共协关系矩阵,并利用该矩阵中元素的取值衡量两个样本之间的相似性.Fred等人[20]首次提出了共协关系矩阵的概念,并提出了证据累积聚类集成算法(EAC),该方法可识别任意形状、大小的簇,但是算法时间复杂度较高.Wang等人[25]对EAC算法进行了扩展,提出了概率累积的方法,该方法考虑了原始聚类中簇的大小,相比于EAC算法效率明显提升.Zhong等人[26]利用样本对之间距离的累积表示它们出现在同一个簇的概率,并以此代替它们出现在同簇中的频率,实现对共协关系矩阵的构建和加权.Huang等人[16]提出了一种基于熵准则的簇不确定性评估方法,并利用该不确定性实现对共协关系矩阵的局部加权.Yi等人[27]构造共协关系矩阵时过滤掉矩阵中的不确定项,随后使用矩阵补全技术完成对不确定项的补全.Li等人[28]以共协关系矩阵为基础,提出一种新的层次聚类方法,通过引入归一化边缘的概念度量簇之间的相似性.Liu等人[29]提出了一种基于共协关系矩阵的谱聚类(SEC)集成算法,在理论上证明了谱聚类与加权K-means算法的等价性.Tao等人[30]提出了一种鲁棒的谱聚类集成算法,该算法通过低秩约束学习共协关系矩阵的鲁棒表示,去除共协关系矩阵中的各种噪声.

基于图划分的聚类集成算法,该类算法的基本思想为将各基聚类结果转换为图,然后在此图上采用不同的图划分算法,以此得到聚类集成结果.Strehl等人[31]提出了3种代表性的基于图划分的聚类集成算法,分别为基于簇相似分割算法CSPA(Cluster-based Similarity Partitioning Algorithm),超图分割算法HGPA(Hyper Graph Partitioning Algorithm)以及元聚类算法MCLA(Meta-Clustering Algorithm).CSPA算法将样本点作为图中节点,以样本点之间的欧式距离来表示边,然后使用METIS[32]算法对图进行划分,以此得到聚类集成结果.HGPA算法同样将样本点作为图中节点,由样本中的每一个簇表示边,同样使用METIS[32]算法进行图的划分.MCLA算法将基聚类的所有簇作为图中节点,边由簇之间共有样本点占整个数据集的比重来表示,然后使用METIS[32]算法将图划分为多个类,最后依据样本点在每个划分类中出现的比例得到聚类集成结果.由于CSPA、HGPA两种算法在构建图时分别只考虑了样本之间、基聚类之间的相似性,可能带来信息缺失.因此Fern等人[33]提出了HBGF(Hybrid Bipartite Graph Formulation)算法,该算法将样本点以及簇作为图中节点来构建二部图,随后使用METIS[32]算法将图进行划分得到聚类集成结果.Huang等人[34]提出一种基于稀疏图表示以及随机游走的图聚类集成算法,样本代表图中节点,边由样本之间相似度表示,利用随机游走方法对每条边加权,最后进行图划分得到聚类集成结果.Mimaroglu等人[35]构建了样本之间的相似图,并通过寻找支点和扩展簇对图进行划分得到聚类集成结果.Yu等人[36]设计了一种基于双亲和传播的聚类集成框架,能够有效处理数据中的噪声,并通过归一化切割算法得到最终的聚类集成结果.

现有聚类集成算法大多只考虑如何将多个基聚类进行集成,往往忽略了基聚类本身质量所带来的影响.然而,在聚类集成中,基聚类质量往往严重影响聚类集成算法的性能.Fred等人[20]首次提出共协关系矩阵的证据累积聚类集成算法(EAC),该方法平等对待各基聚类,整体性能容易受到质量较差基聚类的影响.为了降低低质量基聚类对集成结果的影响,研究人员提出了基聚类加权的聚类集成算法[14-17],为质量较好的基聚类赋予较高权重,同时降低较差基聚类的权重.然而当前聚类集成算法研究中,如何高效地评估各个基聚类的质量,是一个较为困难的问题.为解决以上问题,本文提出一种度量学习引导的加权聚类集成算法,本算法在学习马氏距离度量的同时,考虑不同基聚类结果中样本对的划分,将大多数基聚类结果认为相似的样本对拉近,将基聚类结果认为不相似的样本对推远,在新的马氏距离的投影空间下,评估各基聚类的重要性,并赋予其新的权重.与传统方法不同之处在于,提出的方法将马氏距离度量学习与基聚类赋权的过程融合,从而有效提升了聚类集成算法的性能.

3 度量学习引导的加权聚类集成算法

本节介绍所提算法WEC-ML中所使用的相关符号,构建了聚类集成算法模型,给出了模型的求解过程简述了算法的步骤以及算法的时间复杂度分析.

3.1 模型相关符号定义

给定数据集X={x1,x2,…,xn}∈n×d,其中n表示样本个数,d表示样本维度,xi表示数据集中第i个样本点.对数据集进行T次聚类,得到T个基聚类结果:

P={P1,P2,…,PT}

在T个基聚类中,第t个基聚类的连接矩阵可定义为:

(2)

表示在第t个基聚类中若样本对i和j属于同一个簇,则其对应的矩阵元素值为1,反之则为-1.

Fred和Jain[20]首次提出共协关系矩阵的定义,共协关系矩阵表示样本对在所有基聚类中出现在同一个簇的频率.基于此,集成T个基聚类的共协关系矩阵S可表示为:

(3)

其中,sij∈[-1,1]表示样本i和样本j在T个基聚类结果中出现在同一个簇的频率.sij越大,表示样本i与样本j越相似,反之,越不相似.

3.2 模型定义

现有聚类集成算法大多无法自动评估各基聚类的质量,平等的对待各基聚类,忽略了基聚类质量对于集成结果的影响.在聚类集成过程中,若生成的基聚类质量较差,对集成结果也会有一定影响.为获得或挑选更高质量的基聚类集合,可在基聚类生成阶段挑选高质量的基聚类作为基聚类集合,在集成阶段,通过设计不同一致性函数,对每个基聚类进行评估,赋予不同的权重.

下面给出一种加权共协关系矩阵的定义:

(4)

现有聚类集成算法大多基于欧氏距离空间,通过集成多个基聚类得到聚类集成结果,以提升聚类性能.然而欧式距离空间对数据的所有特征等权重考虑,相比之下,马氏距离考虑特征之间相关性和差异性,可以更好的刻画样本之间的相似性.因此本文受马氏距离度量学习的启发,提出了一种度量学习引导的加权聚类集成算法,该方法在学习样本间的马氏距离度量的同时考虑不同基聚类结果中样本对的划分情况.对应优化问题可表示为:

(5)

本方法将多个基聚类加权过程与马氏距离度量学习统一到一个框架中,两个过程相互指导.此外,模型中还引入了两个正则化项用于指导约束基聚类的加权过程.

因此,目标函数改写为:

(6)

模型中第2项为马氏距离矩阵的正则化项,用于保证矩阵的稀疏性.第3项为各个基聚类权重向量的正则化项,用于约束各个基聚类赋予的权重差异,若权重值过大会赋予较大的惩罚.

3.3 模型求解

提出的模型有两个需要求解的变量,即马氏距离矩阵M以及权重向量α.本文采用迭代交替优化的方法进行模型求解,求解过程如下:

1)固定权重向量α,求解马氏距离矩阵M

当权重向量α固定,去掉无关项,式(6)的优化问题可表示为:

(7)

对M求偏导,并令偏导等式等于零,则有:

(8)

因为权重向量α固定,所以sij值为常量.因此,由式(8)可得:

(9)

2)固定马氏距离矩阵M,求解权重向量α

当马氏距离矩阵M固定,式(6)的优化问题可表示为:

(10)

则有:

(11)

因此,式(6)的优化问题等价于:

(12)

上述优化问题是一个标准的二次规划问题,可以使用常规优化方法[37]求得最优解.

3.4 算法步骤

基于模型求解过程,可以给出度量学习引导的加权聚类集成算法的描述:

输入:数据集X,聚类簇数k,超参数λ及β.

输出:聚类集成结果π.

步骤1.对数据集X运用聚类算法生成T个基聚类,P={P1,P2,…,PT};

步骤2.依据式(2)得到每个基聚类结果对应的连接矩阵Gt;

步骤3.初始化各个基聚类权重值,赋予各个基聚类相同的权重;

步骤4.依据式(4)获得更新加权的共协关系矩阵S;

步骤5.依据式(9)求解更新马氏距离矩阵M;

步骤6.依据式(12)求解更新各基聚类的权重值αt;

步骤7.重复步骤4～步骤6,直到各基聚类的权重值趋于收敛或者达到最大迭代次数;

步骤8.在加权的共协关系矩阵S上执行层次聚类算法,得到最终聚类集成结果.

3.5 时间复杂度分析

本节根据3.4节算法步骤,对所提算法WEC-ML的时间复杂度进行分析,主要根据聚类集成算法基聚类生成阶段(步骤1～步骤3)和一致性函数学习阶段计算(步骤4～步骤8).

基聚类生成阶段,生成T个基聚类的时间复杂度为Ο(Ttc),其中tc表示生成一个基聚类的时间复杂度.基聚类结果转换为连接矩阵的时间复杂度为Ο(Ttg),其中tg表示一个基聚类转换为对应连接矩阵的时间复杂度.因此,基聚类生成阶段时间复杂度可表示为Ο(T(tc+tg)).

一致性函数学习阶段,循环体主要包括3个步骤,即加权的共协关系矩阵S的生成、马氏距离矩阵M的计算更新以及各个基聚类权重αt的更新.

1)加权的共协关系矩阵S的生成为T个连接矩阵与权重向量的相乘相加.因此,更新S的时间复杂度可表示为Ο(T).

2)马氏距离矩阵M的求解为n对向量相乘相加.因此,更新M的时间复杂度可表示为Ο(n2).

3)由于各基聚类权重αt的更新是标准凸的二次规划问题,可以使用椭球法在多项式时间内求解.因此,更新各基聚类权重的时间复杂度可表示为Ο(P(m)),其中P(·)表示一个多项式函数.

假设一致性函数学习阶段迭代次数为Niter,因此一致性函数学习阶段的时间复杂度可表示为Ο(Niter(T+n2+P(m))).

综上所述,所提出算法WEC-ML总时间复杂度为Ο(T(tc+tg))+Ο(Niter(T+n2+P(m))).

4 实验结果及分析

为验证度量学习引导的加权聚类集成算法(WEC-ML)的有效性及性能,采用UCI数据集对提出算法进行验证.实验运行环境如下:PC配置为Inter(R)Xeon(R)Gold 6254 CPU@3.10GHz,512GB,系统为Windows10,代码执行软件为MATLAB 2022b.

4.1 数据集与评价指标

本文选取了Breast、Control、Dermatology、Ecoli、Glass、Ionosphere、Iris、Wine、Yeast Appendicitis、Newthyroid、Wdbc 12个UCI数据集进行实验分析,数据集的详细描述如表1所示,实验中为了避免数据集中特征之间差异对集成结果造成影响,对所有数据集进行了归一化处理.

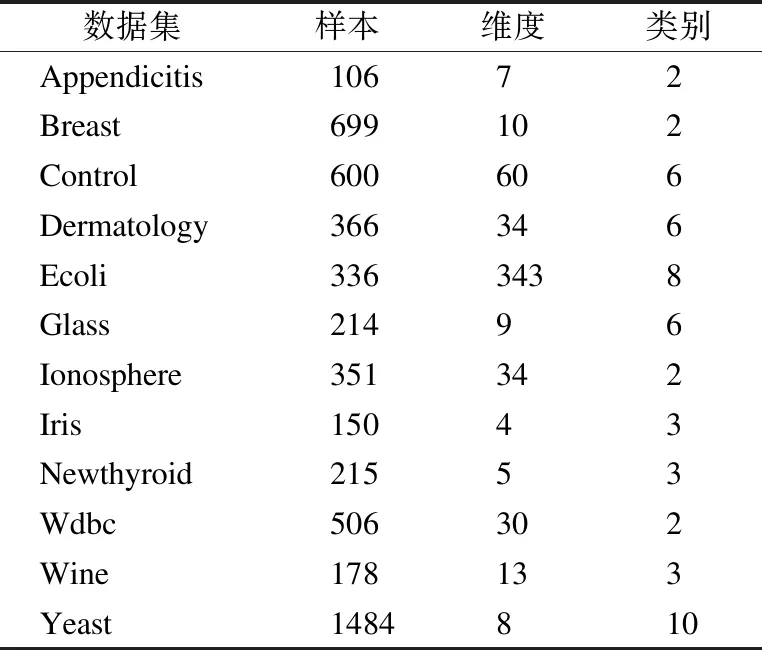
表1 数据集详细信息

为评估聚类集成结果的准确性,采用调整兰德系数(Adjusted Rand Index,ARI)[38]、标准互信息(Normalized Mutual Information,NMI)[31]两种常用的聚类评价指标对其进行评价.ARI与NMI结果取值范围均为[0,1],结果越接近1,集成结果与真实结果越接近,说明算法的集成效果越好.

调整兰德系数(ARI)通过计算两个聚类结果中的样本对是否属于相同簇来获得.从广义角度讲,ARI用于衡量两个数据分布的相似程度.其计算公式如下:

(13)

其中,N11表示样本对既在基聚类π′中属于同簇,同时在基聚类πG中属于同簇的个数;N00表示样本对在基聚类π′中不属于同簇,同时在基聚类πG中也不属于同簇的个数;N10表示样本对在基聚类π′中属于同一个簇,但在基聚类πG中不属于同一个簇的个数;N01表示样本对在基聚类π′中不属于同一个簇而在基聚类πG中属于同簇的个数.

标准互信息(NMI)从信息论角度评估真实聚类结果与现有聚类结果的相似度,其计算公式如下:

(14)

其中,Nij表示聚类结果第i个簇中包含原数据集类标签为j的样本总数,Ni表示聚类结果中第i个簇的样本总数,Nj表示原数据集类标签为j的样本总数,N表示样本总数.ks和kt分别表示聚类得到的簇个数和原数据集的类个数.

4.2 实验设置

实验中,每个基聚类的初始化权重设置为αt=1/T,t=1,2,…,T.权衡参数λ及β参数范围均为{10-4,10-3,10-2,10-1,100,101,102,103,104}.本文使用K-means算法生成T个基聚类,其中集成规模T设置为20.为了保证各个基聚类之间的差异性,本算法聚类簇数k值的选择范围为[K,50],其中K为数据集真实簇数.为保证实验的公平性,对比算法涉及到的实验参数均与其原文保持一致.为了减少到实验的随机性的影响,每个算法均运行20次,计算平均ARI、NMI值及对应的标准差.

4.3 对比实验

为了验证所提WEC-ML算法性能,将其与EAC[20],LWEA[16],MCLA[31],MDEC-HC[23],NMFC[39],PTGP[36],RSEC[30]聚类集成算法进行比较.实验结果如表2及表3所示,表中每个数据集的最优结果已加粗展示,括号内为标准差.

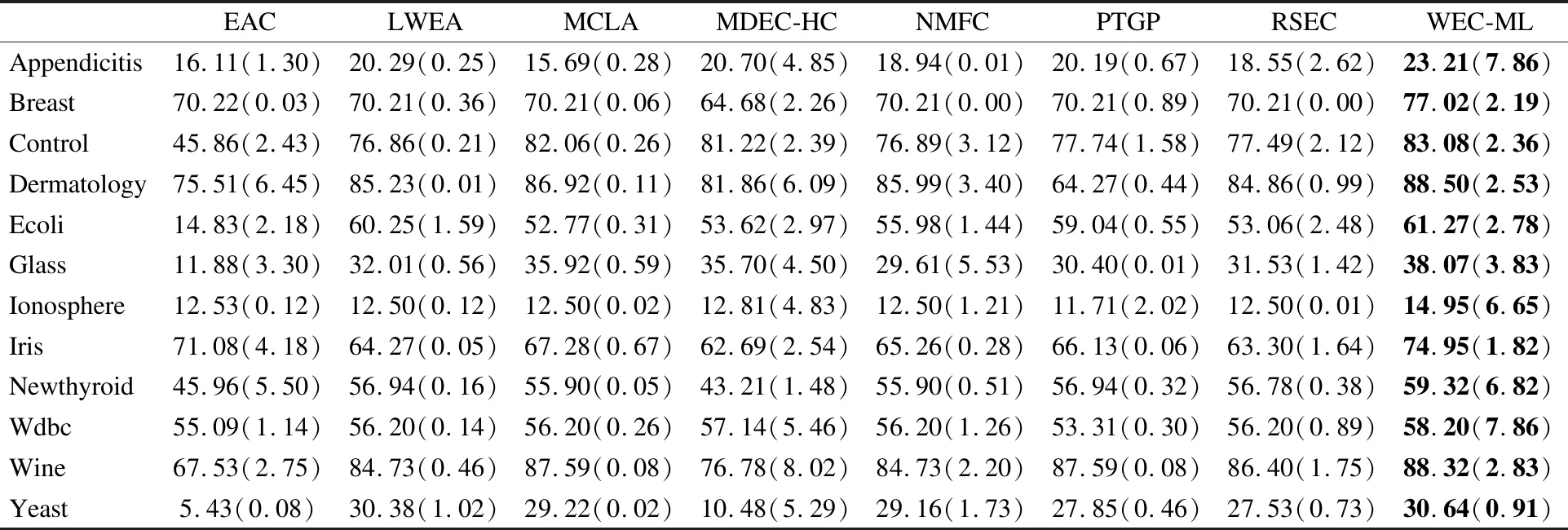
表2 不同算法在数据集上的平均NMI值(T=20)

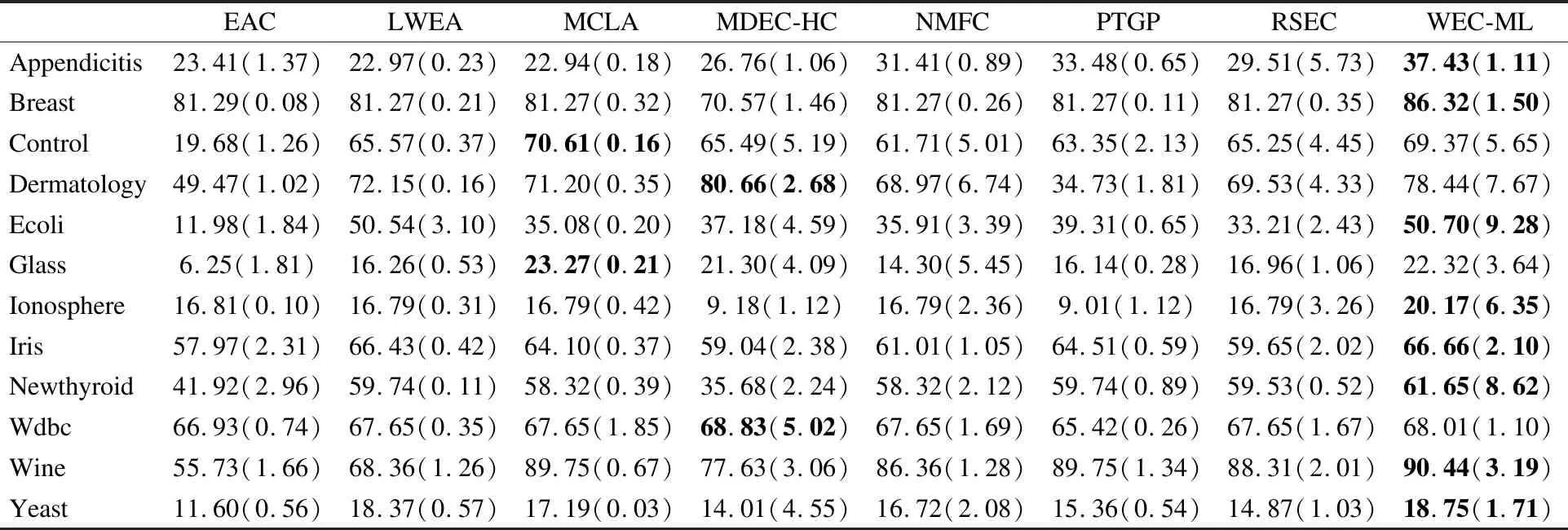
表3 不同算法在数据集上的平均ARI值(T=20)

通过分析表2和表3的实验数据可得,相比于对比算法,本文提出的WEC-ML算法在所有数据集上的NMI值均有显著的提升.虽然在Control、Dermatology、Glass以及Wdbc数据集上WEC-ML算法的ARI值不是最优但仍是次优结果.此外,相比于各基聚类等权重考虑的证据累积(EAC)、非负矩阵分解(NMFC)算法,WEC-ML算法的NMI、ARI均有明显提升,表明了WEC-ML算法对各基聚类赋予不同权重后再进行聚类集成的有效性.与此同时,相比于基于熵准则加权的聚类集成算法(LWEA),WEC-ML算法也有一定的优势,也表明了所提算法在基聚类加权方面的优势.

4.4 参数敏感性分析

通过对所提算法WEC-ML在每个数据集上采用不同参数得到的NMI值进行可视化展示,进行了参数敏感性分析.在提出的算法中,超参数λ及β会影响模型性能,其中λ用于控制马氏距离矩阵M的稀疏程度,β用于控制各个基聚类权重均衡程度.通过调整λ及β的值,并记录每个数据集的NMI值,实验结果如图1所示.当λ及β取不同值时NMI值有一定程度的波动.由图1可以看出,WEC-ML在Appendicitis、Breast、Ecoli、Iris、Wdbc、Wine数据集上对参数变化较为敏感,并且往往是在λ固定,β不同的情况下,WEC-ML的NMI值比较敏感.而在Control、Dermatology、Glass、Ionosphere、Newthyroid、Yeast数据集上对参数变化不太敏感.

图1 算法在不同参数下的平均NMI值

4.5 集成规模分析以及迭代情况

为进一步评估所提方法的稳健性,比较了不同集成规模下不同聚类集成算法的性能.在不同的数据集上运行不同聚类集成算法,其中,集成规模范围为{10,20,30,40,50},实验结果如图2所示.可以看出,虽然NMFC、MDEC-HC算法在Glass、Wdbc和Wine上部分集成规模优于所提算法,但是在其他数据集上,所提算法与对比算法相比产生了最好或者接近最好的结果.特别是,在Appendicitis、Breast、Ionosphere 以及Iris数据集上,所提算法在不同集成规模下均优于对比算法.并且,随着集成规模的变化,对比实验的NMI值波动明显,而WEC-ML算法的运行效果较为平稳.

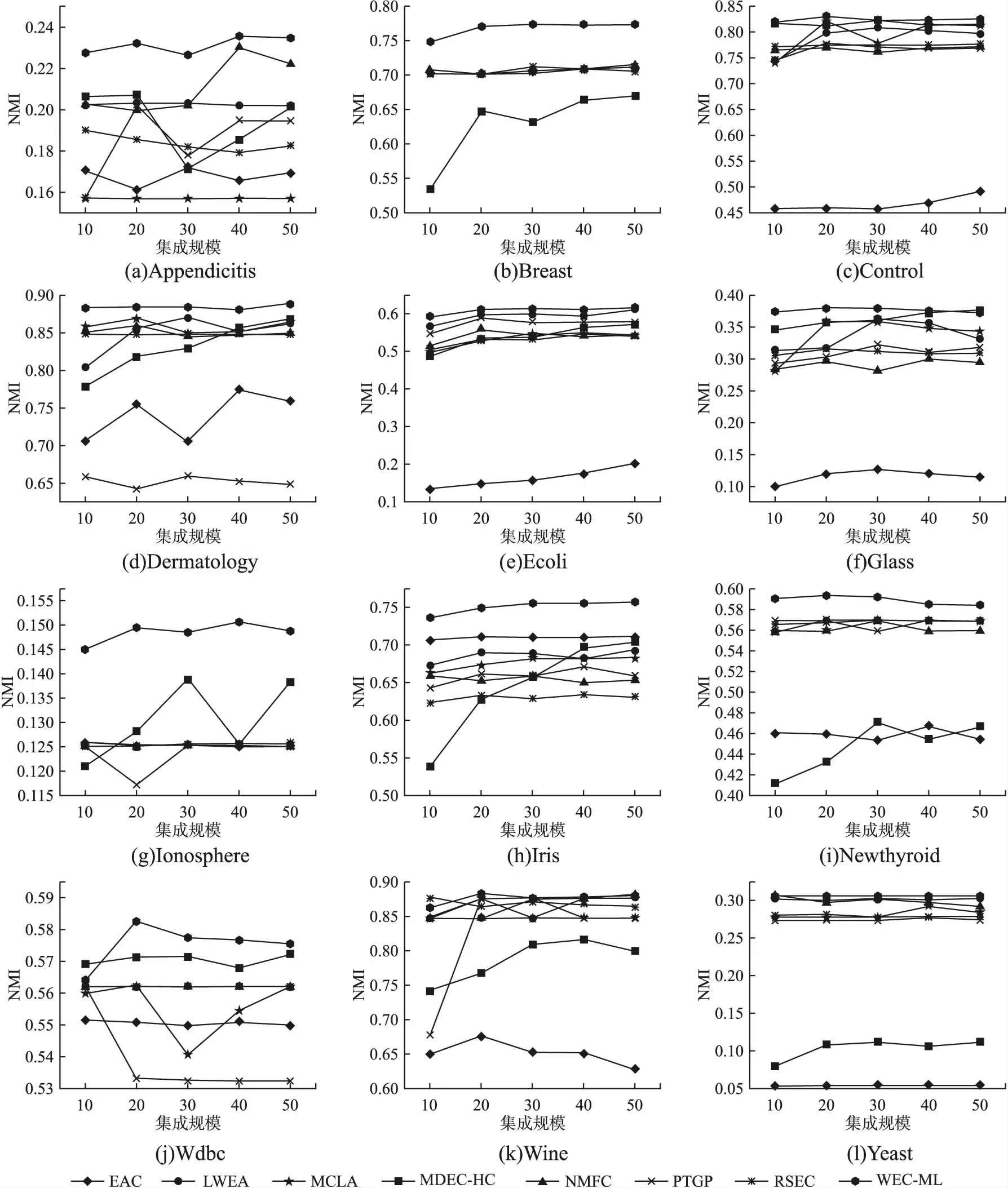
图2 不同算法在不同集成规模下的平均NMI值

通过对各数据集上算法迭代收敛次数的分析,可以得到大部分算法的迭代次数小于5,只有Appendicitis、Wine、Yeast迭代次数分别为9、5、7.表明WEC-ML算法可以在有限时间内求得各基聚类的最优权重.

5 结 论

本文提出了一种度量学习引导的加权聚类集成算法.该算法根据聚类集成结果构建的成对约束学习马氏距离度量,并将马氏距离度量学习与基聚类权重学习整合到同一个优化问题中,实现了二者的相互指导,在充分地挖掘成对约束关系的基础上,同时降低了低质量基聚类对聚类集成结果的不良影响.实验分析表明度量学习引导的加权聚类集成算法的性能优于现有的代表性聚类集成算法.然而,在许多实际问题中简单的应用马氏距离度量难以刻画样本之间的关系,因此如何将本文思想扩展到深度聚类集成算法是一个值得研究的问题.