广义Robertson-Walker时空中具有高阶平均曲率的完备类空超曲面*

张 宁

(河南工学院 理学部,河南 新乡453003)

0 引言

Lorentzian流形是微分流形的重要分支,无论在数学还是广义相对论方面都具有重要的意义,一直以来被众多的几何学家和物理学家关注和研究。此方面的研究也是基于Lorentzian流形中的类空超曲面在广义相对论中的重要性。事实上,Lorentzian几何是广义相对论的几何语言,而其中的类空超曲面扮演着重要的角色。例如,在Einstein场方程的初值公式中,甚至可以说类空超曲面决定了空间的结构。

本文结构如下:第一部分给出广义Robertson-Walker时空及其类空超曲面的一些概念与结论;第二部分证明Robertson-Walker时空中的完备类空超曲面的唯一性;第三部分将第二部分所得的唯一性结果推广到广义Robertson-Walker时空中。

1 广义Robertson-Walker时空及其类空超曲面

由于∂t是类时的单位向量场,则在Σn上存在唯一的一个与∂t具有相同时间定向的类时单位法向量场N,即满足〈N,∂t〉<0。利用Cauchy-Schwarz不等式,可得〈N,∂t〉≤-1。此外,我们定义函数θ:=〈N,∂t〉为Σn的角度函数。

令A:Τ(Σ)→Τ(Σ)是类空超曲面Σn上关于N的形状算子,并且其特征值λ1,…,λn为Σn的主曲率。此外,对于形状算子A,Σn上存在n个代数不变量,即关于A特征值的r阶初等对称函数Sr,定义为

且Σn上的r阶平均曲率Hr被定义为

(1)

故H0=1,H1是Σn的平均曲率。

定义A相对应的牛顿变换Pr:Τ(Σ)→Τ(Σ)为

对于每一个Pr可定义其相应的二阶线性微分算子Lr:C∞(Σ)→C∞(Σ),则对任意f∈C∞(Σ)有

Lr(f)=tr(Pr∘2f)

(2)

故,h在Σn上的梯度为

且 |h|2=θ2-1

(3)

其中,( )Τ是向量场沿Σn的切丛,而||为向量场在上Σn的范数。

为了证明我们的结果,先给出需要的引理。

引理1[10]设ψ:Σn→-I×ρMn是浸入GRW时空-I×ρMn中的类空超曲面。令h是高度函数,σ(t)是扭曲乘积函数ρ(t)的原函数,则

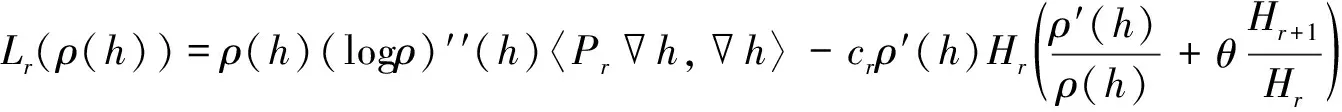
(4)

Lrσ(h)=-cr(ρ′(h)Hr+θρ(h)Hr+1)

(5)

定义1 设ψ:Σn→-I×ρMn是GRW时空中的类空超曲面。如果选取合适的高斯映射N,使得所有的主曲率ki(p0),1≤i≤n同号,则称点p0∈Σn为椭圆点。

此外,GRW时空中-I×ρMn中的类空块是指如下类型的区域:

[t1,t2]×Mn={(t,p)∈-I×ρMn:t1≤t≤t2}

下面的两个引理给出了算子Lr,r≥1是椭圆算子应该满足的几何条件。

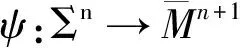
下面的引理给出了浸入GRW时空中的类空超曲面上存在椭圆点的条件。

引理4[10]设ψ:Σn→-I×ρMn是浸入GRW时空-I×ρMn中的类空超曲面。如果ρ(h)在点p∈Σn上取得局部最小值并且满足ρ′(h(p))≠0,则点p为Σn的椭圆点。

为了证明唯一性,还需应用以下结论:Stokes定理的拓展形式,我们将其呈列如下,其中L1(Σ)为Σn上的勒贝格可积函数。

引理5[13]设X为n维完备非紧致的可定向黎曼流形Σn上的光滑向量场,使得divX在Σn上不变号。若|X|∈L1(Σ),则有divX=0。

引理6[13]设u是n维完备黎曼流形Σn上的非负光滑的次调和函数,若|u|∈L1(Σ),则u是常数。

2 Robertson-Walker时空中的唯一性

首先,我们给出Robertson-Walker时空中有关唯一性的结果。

定理1 设ψ:Σn→-I×ρMn是浸入Robertson-Walker时空-I×ρMn中的完备类空超曲面且包含于一类空块中。如果ρ(h)在点p∈Σn上取得局部最小值且满足ρ′(h(p))≠0;并且在Σn上平均曲率H有界,HrHr+1<0,1≤r≤n-1;此外|h|∈L1(Σ)。假设以下两个条件中的任意一个成立:

其中k为纤维Mn的常截面曲率,则Σn为类空片。

证明:首先,根据公式(3)可知θ≤-1。其次,根据引理4,可知Σn上存在椭圆点,由椭圆点的定义和等式(1)可得H2>0。

我们注意到若第二基本形式|A|在Σn上有界,则Pr在Σn上有界。利用H有界和H2>0,结合等式|A|2=n2H2-n(n-1)H2,可得|A|在Σn上有界,从而Σn上存在常数C>0,使得

|Pr(σ(h))|≤Cρ(h)|h|∈L1(Σ)

此外

div(Prσ(h))=ρ(h)〈divPr,h〉+Lr(σ(h))

当Mn具有常截面曲率k,则直接计算可得

(6)

因为HrHr+1<0,1≤r≤n-1,则高阶平均曲率Hr与Hr+1异号。当Hr>0,Hr+1<0时,考虑到椭圆点的存在性,利用引理3和引理4可得r为偶数且Pr-1是负定的。考虑假设条件(i),可知在Σn上div(Prσ(h))≥0。进一步,根据引理5,可知div(Prσ(h))=0,代入公式(6),可得θ=-1,即Σn为类空片。

另一方面,当Hr<0,Hr+1>0时,再次利用引理3和引理4,可得r为奇数且Pr-1是正定的。结合条件(i),可知在Σn上div(Prσ(h))≤0,由引理5,div(Prσ(h))=0,则Σn为类空片。

对于第二个条件(ii),类似于假设条件(i)的推导过程,可得Σn为类空片。证毕。

同时,若Σn上存在椭圆点且高阶平均曲率同号,即HrHr+1>0,1≤r≤n-1,则选取合适的高斯映射N,有Hr>0,Hr+1>0。此时,我们可得如下推论:

推论1 设ψ:Σn→-I×ρMn是浸入Robertson-Walker时空-I×ρMn中的完备类空超曲面且包含于一类空块中。如果ρ(h)在点p∈Σn上取得局部最小值且满足ρ′(h(p))≠0;在Σn上平均曲率H有界且HrHr+1>0,1≤r≤n-1;此外,|h|∈L1(Σ)。假设以下两个条件中的任意一个成立:

或

其中k为纤维Mn的常截面曲率,则Σn为类空片。

3 广义Robertson-Walker时空中的唯一性结果

在本节,我们将Robertson-Walker时空中的有关结论延拓至广义Robertson-Walker时空中,给出此外围空间中完备类空超曲面的唯一性结果。

定理2 设ψ:Σn→-I×ρMn是浸入广义Robertson-Walker时空-I×ρMn中的完备类空超曲面且包含于一类空块中,如果ρ(h)在点p∈Σn上取得局部最小值且满足ρ′(h(p))≠0;在Σn上平均曲率H有界,(logρ)″(h)≥0且|h|∈L1(Σ),若以下两个条件中的任意一个成立:

其中0≤r≤n-1,则Σn为类空片。

证明:类似于定理1的讨论,可知Σn上存在椭圆点且Pr有界。对于条件(i),HrHr+1<0,我们分两种情况讨论:当Hr>0,Hr+1<0时,通过引理3和引理4,可知r为偶数且Pr是正定的。因此,存在常数β>0满足Pr≤βI,利用等式(4),我们有

结合条件(i),则βΔρ(h)≥0。由于类空超曲面包含于一类空块中,可知h是有界的,从而Σn上存在常数C>0,使得|ρ(h)|≤C|h|∈L1(Σ)。根据引理6,可得ρ(h)为常数,故h也是常数。因此Σn是一类空片。

另一方面,当Hr<0,Hr+1>0时,根据引理3和引理4,可知r为奇数且Pr是负定的。因此,存在常数β>0满足Pr≥-βI,再次利用等式(4),我们有

考虑条件(i),可知βΔρ(h)≥0。同理可证Σn是一类空片。

对于条件(ii)的情况,类同于条件(i)的证明,可得Σn是一类空片。证毕。