复杂金属中电阻率的非广延统计模型*

郑亚辉,孙朋强,李沉思,董晓曦

(河南工学院 理学部,河南 新乡 453003)

0 引言

在现代科学技术应用中,材料的导电性能是需要考虑的重要性能之一,在很多情况下,它甚至超过了材料的力学和热学性能。导电材料、电阻材料、电热材料、半导体材料、超导材料和拓扑绝缘材料等,都是以材料导电性能为基础的。描述材料导电性能的重要物理量是电导率或电阻率,二者互为倒数。由于材料的复杂性,在理论上对电导率或电阻率进行研究、明确其主要的影响因素,是极为重要的。

在经典量子统计中,基于自由电子费米狄拉克分布函数,通过能带电子的玻尔兹曼方程的弛豫近似,可以得到金属自由电子的电导率公式,其倒数就是电阻率,电阻率与电子弛豫时间倒数成正比关系。弛豫时间倒数在物理上是可分析的,具有物理实在性,它一般与自由电子格波散射过程有关。格波散射可以看成电子与声子的碰撞过程,由此得到了弛豫时间的大角度散射跃迁表达式[1-2]。

在纯金属材料中,电阻率的一般实验规律是:高温时,电阻率与温度T成正比,低温时电阻率与T5成正比,后者被称为Bloch-Gruneisen定律[3-4]。为了与实验规律匹配,人们提出了各种模型[5-6],用以简化散射跃迁表达式,以得到解析结果。另一方面,在包含杂质的半导体、拓扑绝缘材料中,电阻率呈现出复杂的温度依赖关系,难以用经典统计理论解释。为了得到更符合实验的理论结果,除了在动力学方面进行修正外,另一个途径是提出新的统计方法。

经典量子统计是以金属的自由电子气模型为基础的。如果需要考虑电子之间的长程相互作用或关联,则需要将统计力学加以推广。有意义的一种推广方法是近几十年才出现的非广延统计力学[7],以该理论方法为基础,可进一步建立能描述量子体系统计性质的非广延量子统计理论[8]。本文以非广延量子统计理论为基础,将自由电子气模型推广,通过改进散射模型,讨论复杂金属电阻率的温度依赖问题。

1 非广延量子统计简介

在正式讨论自由电子电阻率问题前,先简单介绍一下非广延量子统计理论。在非广延巨正则系综内[8],基本的分布函数为

(1)

其中的巨配分函数是

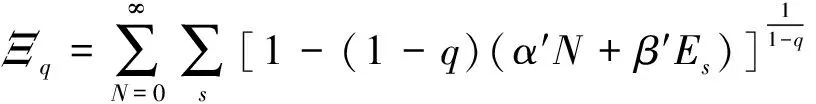
(2)

这里的s代表系统的不同量子态,广义拉格朗日乘子定义为[8]

(3)

而Tsallis因子

(4)

平均粒子数和系统内能定义为

(5)

在一个近独立的量子系统,粒子数和能量可以表示为

(6)

在巨正则系综内,占据数的分布{an}是不确定的,因此必须考虑巨正则求和中所有的可能性。根据平均值的非广延定义(5),给定量子态的平均占据数可定义为

(7)

引入如下参数变换

(8)

在这个变换式的左端,求和项正比于整个系统在给定占据数分布时的总自由度。提出这个变换的主要目的是,用新的非广延参数ν替换非广延参数q。因此,假定整个系统使用相同的ν值,这意味着q值随着系统占据数分布的变化而变化,而同时在占据数分布固定的子系统中,q值又是不变的。进一步将(8)对所有可能的占据数分布取平均,可得到一个简单的二参数关联式

(9)

其中,N是系统平均粒子数,d是单粒子自由度。上述平均实际上也对q取平均了,也即此时的q值对整个系统的来说是不变的。

定义如下非负实数,作为新指数函数的底

(10)

则有

(11)

对非广延玻色系统,有如下玻色统计表达式

(12)

此时的巨配分函数为

(13)

为了得到解析结果,作为一级截断,已经忽略了指数部分对Tsallis因子的依赖。Tsallis因子与巨配分函数的自关联关系由下式给出[9-10]

(14)

2 自由电子电导率的改进模型

为给出改进模型,先介绍自由电子电导率的经典模型,它由下式描述[1]:

(15)

其中的ne是自由电子数密度,qc是电子电荷,τ是电子弛豫时间,m*是电子有效质量。该式适用于各向同性金属晶体,其倒数就是电阻率。也就是说,电阻率与弛豫时间倒数成正比。

弛豫时间可解释为自由电子与晶格格波的散射时间,即自由电子与声子的自由碰撞时间。考虑各向同性弹性散射情况,弛豫时间可表示为[1-2],

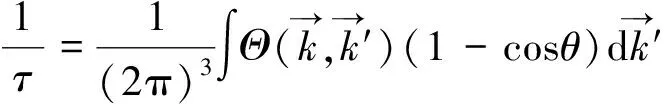
(16)

其中的Θ是电子在散射过程中由k态到k'态的跃迁几率,θ是电子的散射角。现在对上述模型做出改进。假定散射跃迁几率是各向同性的,则有

(17)

这里的δ函数来自于量子力学微扰论,其中已经忽略了声子能量,A是只与碰撞前后电子波数有关的常数项。跃迁几率与经典碰撞频率成正比,即与单位时间内电子和声子的碰撞次数成正比。后者又与声子的平均浓度成比例。故此上式中出现的n代表声子的平均浓度。

考虑到(17),式(16)可修改为

(18)

对于各向同性晶体,能态密度为

(19)

因此有

(20)

该式就是我们进一步讨论的基础。

3 基于非广延玻色统计的温度依赖关系

为了具体应用,在广义玻色统计表达式(12)式中引入如下拉格朗日关系[9-10]:

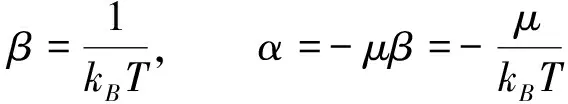
(21)

其中的kB是玻尔兹曼常数,μ是化学势,T是热力学温度或拉格朗日温度。声子的化学势为零,如果暂时忽略指数部分对Tsallis因子的依赖关系,则在给定能量下的声子数目为

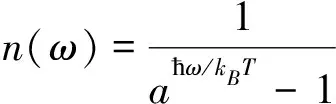
(22)

应用德拜模型,声子的谱密度可写为[11]

(23)

其中的cs代表声速。设系统的总自由度为3N,则上式满足

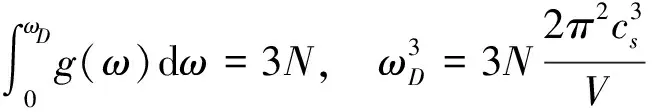
(24)

其中的ωD是德拜频率。

根据德拜模型,声子浓度为

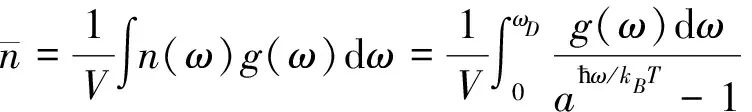
(25)

另一方面,设声子波数为qs,且满足ω=csqs,则声子波数的平均值为

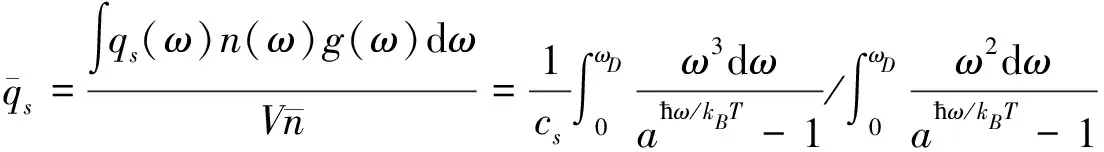
(26)

上述积分很难给出解析结果,需要考虑温度的两种极端情况。首先是高温情况,在这种情况下,所有格波,即所有声子都会被激发,这意味着式(20)中的散射角取遍了所有可能的角度:

(27)

然后是低温情况,在这种情况下只有低频格波被激发,声子动量很小,散射角度也很小。散射角的积分上限无法估算。为此,可将散射角看成立体角的函数,取其平均值如下:

(28)

如图1所示,如果只考虑电子散射的正规过程,在小角度散射情况下,有

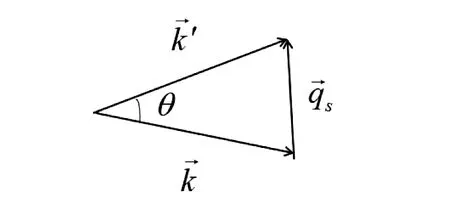
图1 电子散射的正规过程

(29)

因此有

(30)

在低温极限,上式的积分上限可取无穷大,因此可得

(31)

综上所述,在高温情况下,金属电阻率与T成正比;在低温情况下,电阻率与T5成正比。这个结论与经典统计给出的结果相同,不同之处是上述结果中多了一个与非广延参数相关的修正。这个结果没什么新奇之处,也不能解释复杂金属对上述温度依赖关系的偏离情况。为此,需要考虑Tsallis因子的修正效应。

4 Tsallis因子修正对温度依赖关系的影响

为了分析Tsallis因子的修正效应,将式(13)写成对数形式,并将求和化为积分,即

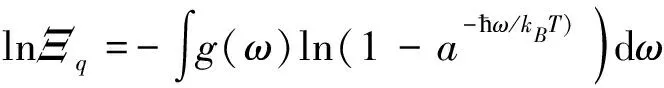
(32)

此外,对复杂金属的晶格振动,取d=6,式(9)变成了

(1-q)3N=1-ν

(33)

在高温情况下,有

(34)

此时声子的总内能可用经典结果近似,即U=3NkBT。考虑到(14)和(33)式,Tsallis因子可以写成如下形式:

(35)

此时的弛豫时间为

(36)

在非广延参数ν偏离1不远的情况下,该式表明金属电阻率对温度的依赖略微偏离了其一次方。这是很有意思的结果。需要注意的是,在一般复杂金属中,非广延参数ν偏离1并不远。

在低温情况下,

(37)

另一方面可以证明,在Tsallis因子一级截断条件下,声子气体的内能为[8]

(38)

根据上述两个结果,有

(39)

此时的弛豫时间为

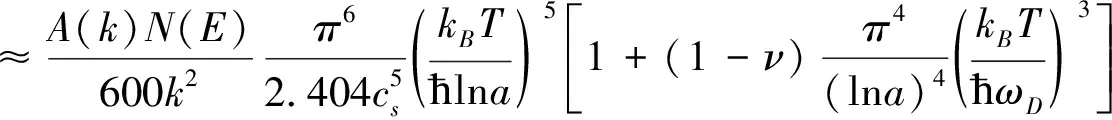
(40)

同样,在非广延参数ν偏离1不远的情况下,上式表明电阻率对温度的依赖出现了一个很小的附加项,它与温度的8次方成正比。为了看清楚非广延参数对电阻率温度依赖关系的影响,需要对上述结果进行数值计算,并画出变化曲线。

5 数值计算

为了进行数值计算,需要忽略次要因素,对弛豫时间表达式(36)和(40)做无量纲化处理。在高温情况下,有

(41)

其中的无量纲电阻率和无量纲温度分别定义为

(42)

同样,在低温情况下有

(43)

在这里,为了精确并没有采用近似形式,其中的无量纲电阻率定义为,

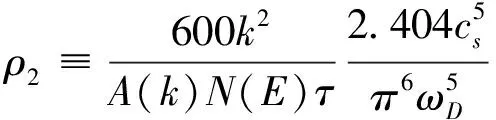
(44)

可以发现,t是热力学温度与德拜温度的比值。在高温阶段这个比值较大,在低温阶段该值较小。图2给出了高温电阻率随温度变化的三条曲线,由上到下,分别对应非广延参数ν=0.90、ν=1.00及ν=1.10时的情况。该曲线族显示出电阻率对非广延参数的敏感依赖特征,这种特征在极高温区非常明显。从数值模拟角度来看,这种敏感依赖特征来自于(41)式中的幂律性质。类似地,图3给出了低温电阻率随温度变化的三条曲线,由上到下,分别对应非广延参数ν=0.99、ν=1.00及ν=1.01时的情况。这个曲线族也显示了温度对非广延参数的敏感依赖性,且在接近德拜温度的温区尤为明显。从(43)式可以看到,这种依赖特征主要来于其中的(1-ν)项。

图2 高温电阻率随温度变化曲线

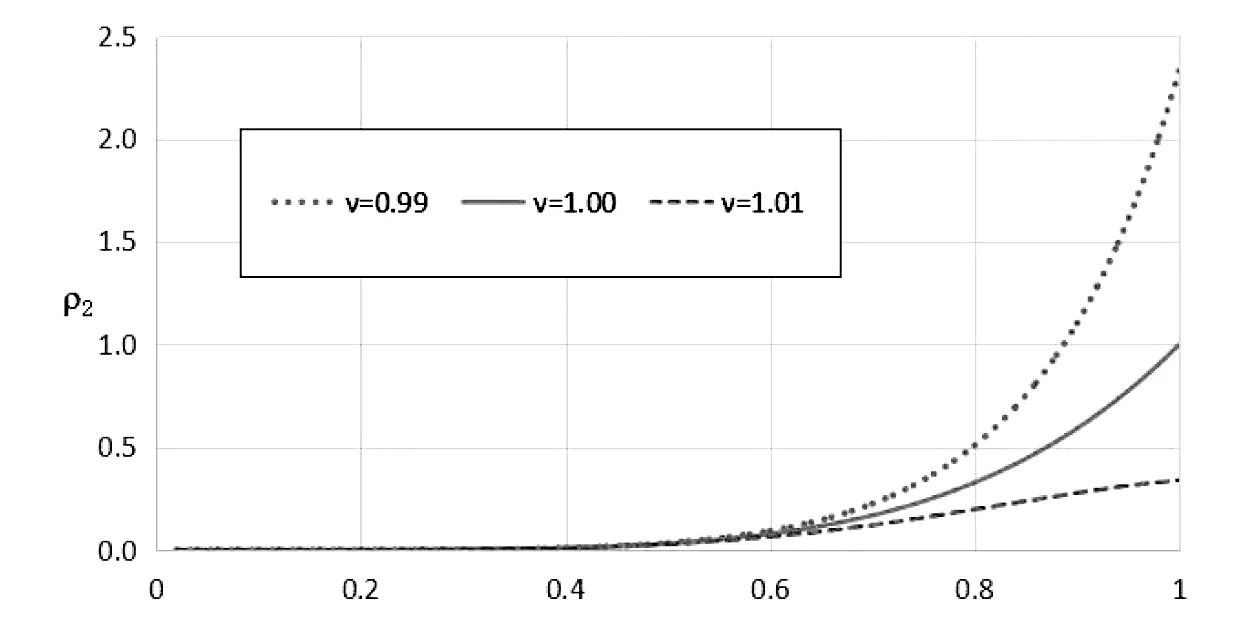
图3 低温电阻率随温度变化曲线

整体来看,金属电阻率会随着非广延参数减小而增加。从物理上来说,电阻率增加意味着散射频率的增加,也就是说,非广延参数减小与更频繁的晶格散射相关联。这表明此时的金属晶体整体上有收缩的趋势,这暗示了晶格常数略微减小或者晶格作用强度略微增加。与此同时,电子之间的长程相互作用表现为吸引力。与此相对,非广延参数增加与导致电阻率减小,晶体有整体膨胀的趋势,暗示了晶格常数的增加和晶格作用强度的减弱,电子之间的相互作用表现为排斥力。

6 结论

在本文中,基于非广延量子统计理论,提出了复杂金属电阻率的电子散射模型的改进型。在该模型中,电子散射几率是各向同性的,仅是电子能量的函数,且与声子平均浓度和电子态密度成正比。在高温情况下,所有格波都被激发,散射角取所有可能的数值;在低温情况下,仅有低频格波被激发,只需要考虑小角度电子散射。此时的散射角需看成立体角的函数,并将散射角积分与其平均值联系起来;小角度散射情况下,角度与声子平均动量成比例。

根据这个改进模型,本文得到了电子自由碰撞时间倒数的解析表达式,它与金属电阻率成比例。在没有考虑Tsallis修正时,该表达式给出的结果本质上与经典表达式相同,都能解释一般金属中电阻率的实验规律:高温时与T成比例,低温时与T5成比例。然而在引入Tsallis修正后,得到了新奇的理论结果,即在高温时电阻率与T2-ν成比例;在低温时电阻率包含两项,第一项较大,与T5成比例,第二项较小,与T8成比例。

通过数值计算,分别给出了高温电阻率和低温电阻率随温度的变化关系曲线。该曲线表明,电阻率敏感依赖于非广延参数ν的取值,它会随着该参数的减少而增加,随着参数的增加而减少。非广延统计理论的基本假设是,复杂系统的统计规律会因其在相空间或真实时空的长程关联而发生改变,从而脱离经典的玻尔兹曼统计。这种脱离主要体现在非广延参数偏离1(即1-ν)的程度上。同时,这种偏离可以跟具体的动力学过程或系统构型联系在一起。如在自引力气体系统[12],偏离量(1-ν)与系统的温度梯度及引力势梯度直接关联。而在实际气体研究中[13],该偏离量(1-ν)与分子间的范德瓦尔斯力关联。

在复杂金属材料中,受各种复杂机制影响,如电子数密度的增加、重离子掺杂、长程电子耦合等,整个晶体出现了长程关联。这种关联一方面导致统计规律的改变,另一方面在动力学上体现为整体排斥或收缩效应,具体到晶格上就是晶格常数及晶格强度的改变。具体来说,非广延参数的减少,来自晶格常数的减少或晶格强度的增加,这导致了晶体整体的收缩、电阻率的增加及碰撞率的增加。反之,非广延参数增加,来自晶格常数的增加或强度减少,晶体整体表现为膨胀、电阻率减少、电子碰撞率减少。

由于非广延参数可以跟很多复杂性机制联系起来,本文的结果在复杂金属材料、拓扑绝缘材料、复杂半导体材料、超导材料及复杂电阻材料等包含复杂性机制的材料中有重要应用。