北京地区砂卵石地层新建地铁隧道小角度下穿施工时既有地铁隧道的变形规律及控制措施

刘 博

(天津铁道职业技术学院,300240,天津∥讲师)

新建隧道小角度近距离下穿既有隧道的施工,极易引发既有隧道变形及开裂等,需要有效控制下穿施工对既有隧道的影响。

国内外学者对隧道下穿施工进行了大量研究。文献[1-7]研究发现,地层类型对结构沉降有较大影响。北京地区砂卵石地层分布较广[8],然而对隧道在砂卵石地层下穿既有隧道施工的变形及控制的研究却相对较少。为了研究砂卵石地层中新建隧道小角度下穿既有隧道施工的变形规律及不同控制措施的控制效果,本文依托北京某地铁区间隧道小角度、近距离下穿既有地铁区间隧道项目(以下简称“下穿项目”),基于现场监测数据对既有隧道的变形进行分析,采用数值分析的方法建立曲线隧道小角度下穿三维数值模型,研究下穿叠交夹角对既有隧道变形的影响,并对比分析不同控制措施的控制效果,为实际施工提供参考。

1 工程概况

下穿项目的隧道位置关系如图1所示。既有隧道采用盾构法施工,管片内径为5.4 m,厚度为0.3 m,左、右线间距约为14.5 m,所在地层为黏土层。新建隧道采用盾构法施工,隧道外径为6.4 m,管片厚度为0.3 m,左右线间距约为18.0 m,覆土厚度约为23.7 m。

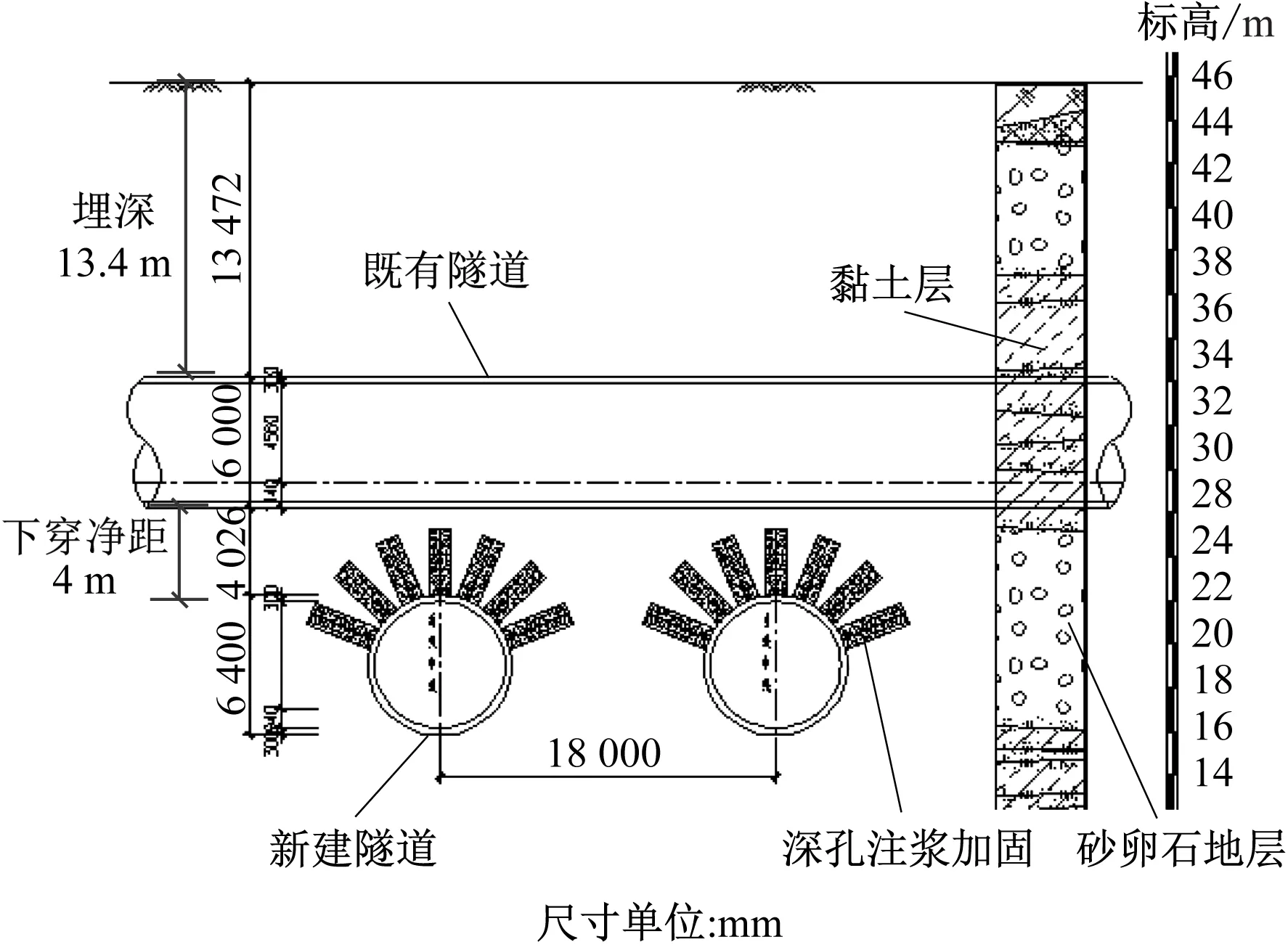
图1 下穿项目的隧道位置关系图

2018年5月17日,新建隧道即将下穿既有隧道,开始监测既有隧道变形;5月21日开始下穿右线隧道;5月26日开始下穿左线隧道;6月11日,新建隧道已经完全穿过既有隧道,且既有隧道变形不再变化,停止监测。在下穿项目中,新建隧道与既有隧道的平面交角约为47°,垂直净距约为4.0 m。新建隧道下穿段主要位于砂卵石地层。在穿越范围采用同步注浆和深孔注浆相结合的方法对土体进行加固。

2 变形规律

2.1 建立数值模型

根据地层结构,通过MIDAS GTS软件建立下穿项目的数值模型,如图2所示。在模型中,地层及注浆区采用实体单元模拟,隧道管片采用二维板单元模拟。地层参数根据地质勘探资料确定。模型的相关材料参数及本构模型见表1。

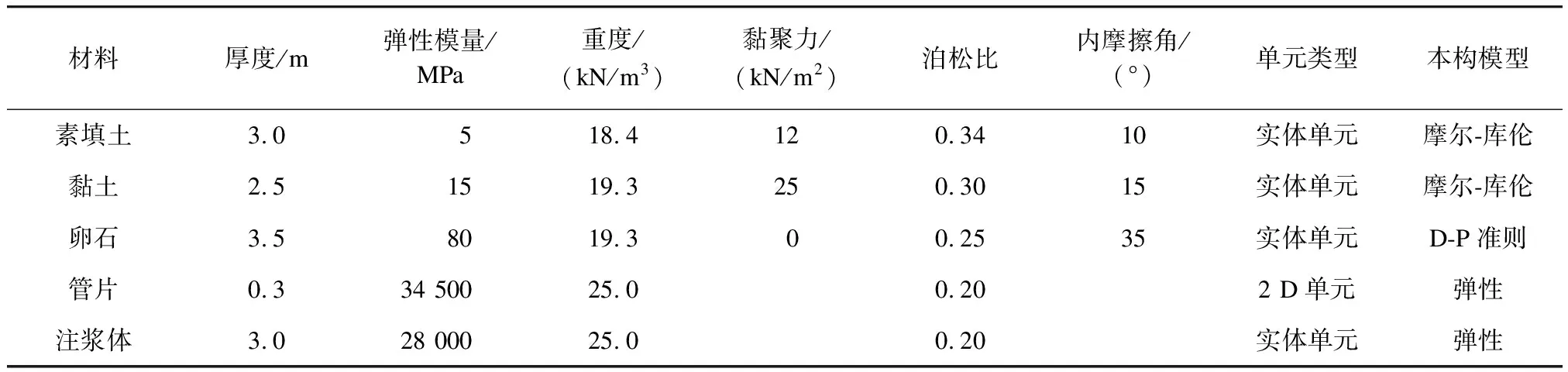
表1 模型的相关材料参数、单元类型及本构模型

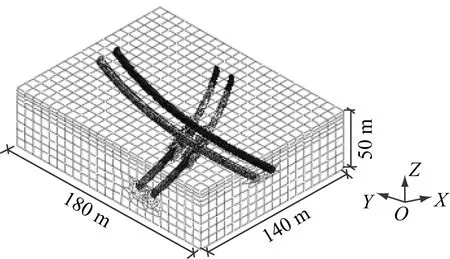
图2 下穿项目的数值模型

数值模型上表面为自由边界,4个侧面为法向约束,地面为固定约束。数值模型尺寸为180 m×140 m×50 m,采用混合网格划分,共划分了46 266个网格,20 486个节点。数值模型中,新建隧道与既有隧道的直径均为6.0 m,既有隧道的埋深为13.4 m。由于现场实际水位较低,水压较小,对变形的影响不大,故模拟计算未考虑地下水的影响。

2.2 数值模型的模拟计算结果

经过数值模型的模拟计算,得到新建隧道斜向下穿通过后新建隧道与既有隧道的竖向位移云图,如图3所示。由图3可以看出,新建隧道的拱顶发生沉降,拱底发生隆起;既有隧道整体沉降,且最大沉降发生在叠交区域正上方,叠交区域两侧的土体变形相对较小。

图3 既有隧道竖向位移云图

2.3 实测数据分析

图4为下穿项目的测点布置平面图。根据近密远疏的原则,既有隧道结构竖向位移监测断面自穿越集中部位中心向两侧布置,每个监测断面设置1个测点。竖向位移测点采用普通沉降测量标志,位于区间隧道管片螺栓上。测点布设不对管片造成损伤。隧道结构竖向位移采用精密水准仪监测:施工前获取3次以上初值;盾构穿越施工期间,监测频率不少于4次/周。

图5为既有隧道结构的竖向位移监测值变化曲线。

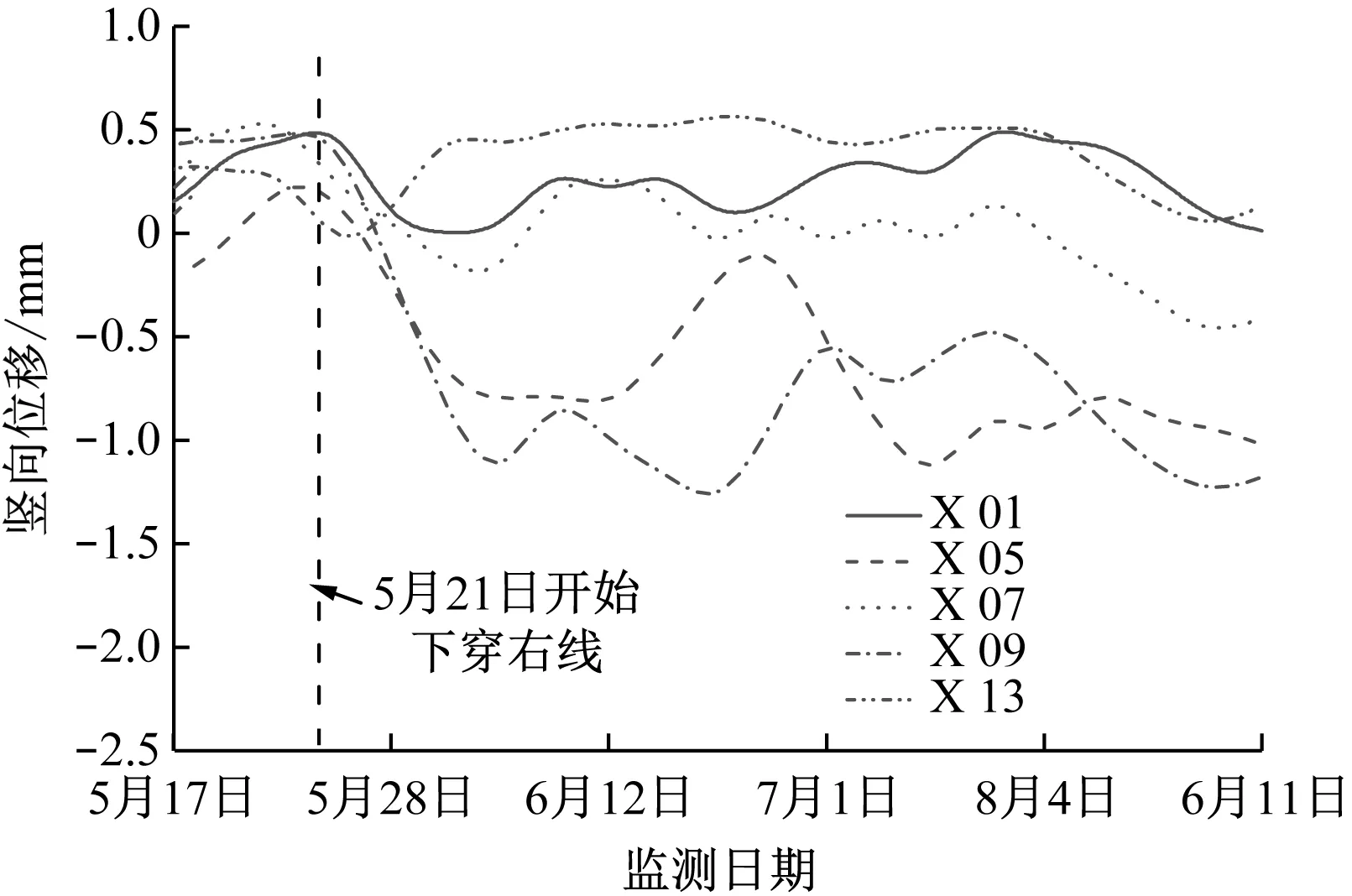
a) 右线

由图5可知:5月21日,新建隧道开始下穿既有隧道的右线,穿越段上方既有隧道出现少量沉降,两侧位置略有隆起,竖向位移值约为0.5 mm,此时左线隧道还未被下穿,以隆起为主,竖向位移值约为0.6 mm;5月26日,新建隧道下穿既有隧道左线,此时左线隧道开始出现沉降,右线隧道出现较大变形,约为0.5 mm;之后随着新建隧道的继续推进,左右线隧道沉降均持续增大;6月10日时,沉降基本达到最大值,右线隧道最大竖向位移值为-2.0 mm,左线隧道最大竖向位移值为-1.5 mm。最大沉降主要集中在穿越段上方位置,而下穿区两侧的既有隧道变形很小。这说明下穿施工对正上方结构影响较大,距离下穿区越远,结构所受影响越小。

2.4 实测结果与模拟结果对比

为了更直观地进行对比,绘制既有隧道竖向位移的实测值变化曲线与模拟值曲线,如图6所示。

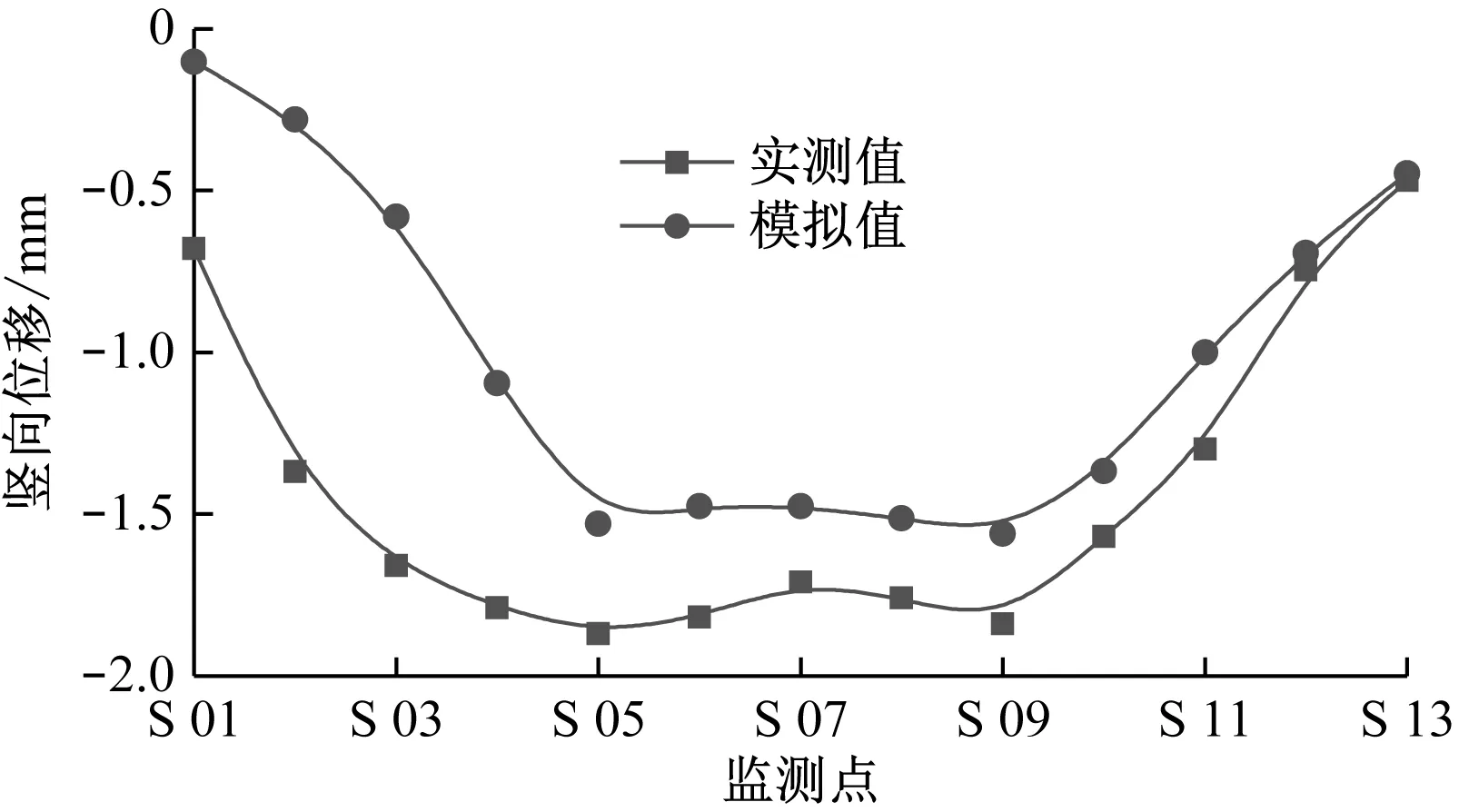
a) 左线

由图6可以看出:既有隧道左右线的竖向位移分布规律基本一致,均呈现出新建隧道正上方沉降大,两侧沉降小的槽状分布。既有隧道右线的最大竖向位移模拟值为-1.7 mm,最大竖向位移实测值为-1.9 mm;既有隧道左线最大竖向位移模拟值为-1.5 mm,最大竖向位移实测值为-1.7 mm。由此可见,模拟值与实测值非常接近,说明数值模型的计算准确性很高。本文将利用数值模型进一步分析隧道叠交角度的影响,以及各变形控制措施的效果。

3 叠交夹角的影响

为了研究新建隧道斜向下穿时,新建隧道与既有隧道的叠交夹角α对既有隧道结构沉降的影响,本文按不同α设置了4种叠交工况,模拟得到下穿施工完成后隧道的竖向位移云图及沉降槽曲线,如图7及图8所示。

a) α=30°

a) 右线

4种工况下既有隧道的最大竖向位移模拟值分别为-2.9、-2.4、-2.1、-1.7 mm。进一步分析可知,α越小,隧道间叠交面积越大,上部隧道沉降槽底部越宽,竖向位移值也越大。

此外,图7的4个斜穿工况中,既有隧道结构的沉降槽向新建隧道偏角方向偏移。这是由于α变小后,新建隧道与既有隧道的距离减小,从而加剧了新建隧道施工对既有隧道的扰动影响。

4 变形控制措施

4.1 建立数值模型

由上述分析可知,新建隧道小角度斜交下穿施工时,既有隧道结构变形更加显著,极易影响既有线的运营安全。在此情况下,采用传统的深孔注浆措施难以有效控制既有隧道的结构变形,通常采取管棚加固、注浆抬升和水平旋喷桩加固等变形控制措施[9]。对此,本文通过数值模型进行模拟,进而分析α=47°时不同变形控制措施的效果。

不同变形控制措施的数值模型及说明见表2。

表2 不同变形控制措施的数值模型及说明

4.2 变形控制措施的效果

经过数值模型的计算,得到下穿项目采取不同变形控制措施时的既有隧道最大竖向位移曲线,如图9所示。

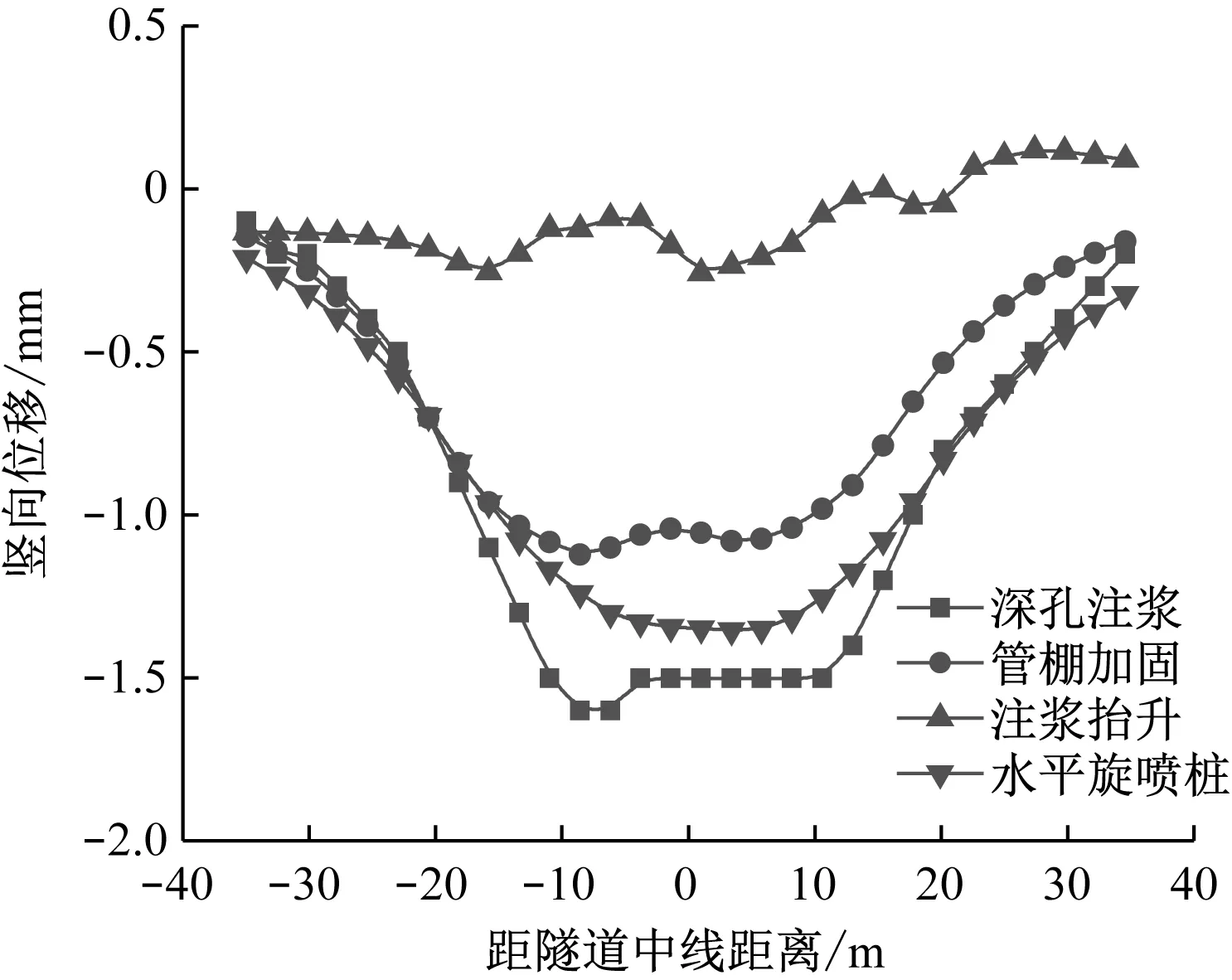
a) 右线

由计算结果可知,采用注浆抬升措施时,既有隧道最大竖向位移仅为-0.35 mm,该措施效果明显最优。经分析,砂卵石地层渗透系数大、孔隙率高,故注浆浆液容易进入孔隙中,注浆压力易于在孔隙中传递;注浆抬升注浆压力大,且需持续保压注浆,可以使沉降的地层抬起,而其他方法仅起到了限制沉降作用,故注浆抬升法效果最好。管棚加固措施的效果次之,相应的既有隧道最大竖向位移为-1.12 mm。这是由于管棚本身具有一定的支撑能力。深孔注浆措施及水平旋喷桩措施的变形控制效果最差,既有隧道的最大竖向位移为-1.50 mm。这是由于两种措施的注浆效果差,且未持续保压注浆,浆液易散失。

根据模拟计算结果,在北京地区砂卵石地层隧道下穿施工时,建议采用注浆抬升措施来加固地层进而有效控制隧道掘进对上部既有隧道变形的影响。

5 结论

1) 下穿区正上方既有隧道变形较大,下穿区两侧既有隧道变形很小,说明下穿施工对正上方结构影响较大,距离下穿区越远,结构受影响越小。

2) 数值分析及监测结果得到的既有隧道变形规律及竖向位移值基本吻合,验证了模型的准确性。

3) 叠交角度越小,隧道间叠交面积增大,上部隧道沉降槽底部越宽,且竖向位移值也越大。

4) 对比分析4种变形控制措施的沉降控制效果,发现注浆抬升效果最优。在北京地区砂卵石地层隧道下穿施工时,建议采用注浆抬升技术加固地层。