城市轨道交通ZC故障场景下列车运行全过程调整方法*

刘 循 楚彭子,2

(1.上海申通地铁集团有限公司技术中心,201103,上海; 2.同济大学电子与信息工程学院,201804,上海∥第一作者,高级工程师)

凭借安全、准时、高效的运营服务,城市轨道交通已成为大都市公共交通骨干。受列车运行间隔较小、不同线路列车共线运行等影响,当发生控车设备故障时,会导致列车运行延误时间较长,需及时调整列车运行方案,降低对运营的不良影响。

针对列车延误场景,文献[1]借鉴“沙丁鱼群”运动效应与仿真技术探讨了列车运行调整自组织机制。文献[2]构建了以总延误时间和延误恢复时间最小为目标的列车运行调整方法。文献[3]以最小化列车延误对乘客的负面影响为目标,结合列车延误恢复和乘客选择行为探讨了列车运行调整问题。文献[4]以提高列车到发均衡性与减少总延误时间为途径,探讨了借助备车替代故障列车的列车运行调整方法。文献[5]建议列车跳停部分车站,以加快列车周转,并构建了考虑列车运行效率与服务乘客数量的优化模型,设计了联合数学规划求解器Gurobi的算法。

现有研究大多假设站间运行时分可在一定范围内任意取值,而实际上列车通常依据预存的推荐速度曲线运行[6]。同时,未充分考虑不同列车延误场景的特有限制因素。基于此,本文以城市轨道交通运营重点关注的ZC(区域控制器)故障场景为例,结合该场景下列车运行限制因素与速度控制策略(预存的推荐速度曲线),研究列车运行全过程调整方法,并针对具体算例在线路上的运用效果进行仿真分析,以期指导城市轨道交通的运营实践。

1 模型准备

ZC主要负责CBTC(基于通信的列车控制)列车运行间隔安全控制。由于ZC故障时,列车运行安全防护相较于正常运营时更为复杂[7],因此,ZC故障对城市轨道交通运营影响较大。考虑ZC故障的列车限速运行方案如图1所示,某线路突发ZC故障,导致列车不能正常通过S6至S9区域。为维持运营,列车可限速通过ZC故障区间,并及时恢复至正常驾驶模式。以常见的RM(限制人工驾驶)模式为例,列车可在进入故障区域前切换为RM模式,限速驶出该故障区域后切换回正常模式。本文以列车限速通过ZC故障区域为条件,研究ZC故障发生后列车运行方案的全过程调整模型。

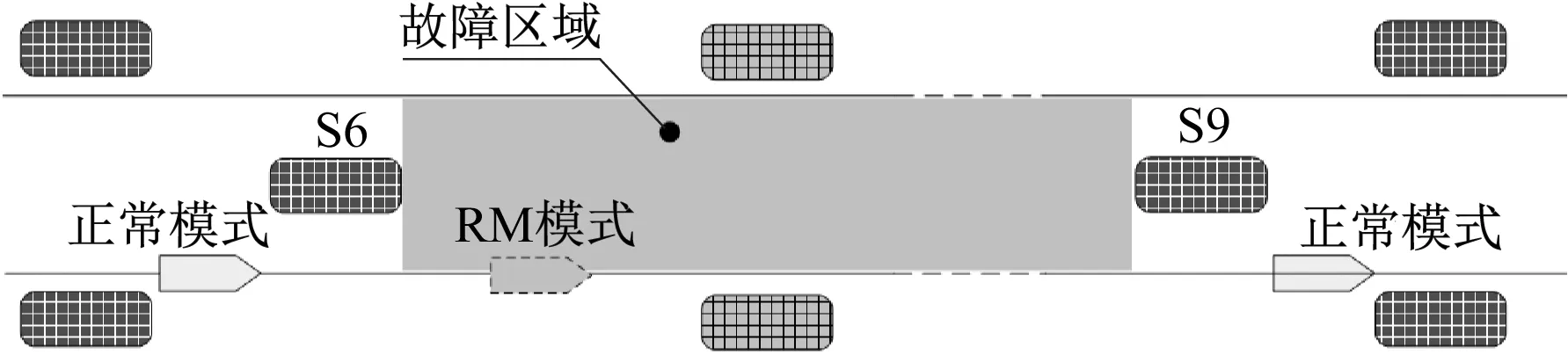
图1 考虑ZC故障的列车限速运行

1.1 基本假设

假设1:列车能够较好实现正常速度控制策略(例如预存的推荐速度曲线),且已知不同策略下的站间运行时分。

假设2:列车运行顺序已知,无“跳停”运行情况,不变更列车运行交路。

1.2 符号定义

1) 集合:车次集合N,索引为i;车站集合S,索引为j;故障发生后车次i途径车站集合Si;故障区域内所涉车站集合Sd,所包含车站的前方第一站区间需限速运行;列车离开车站j时能采用的运行控制策略集合Cj;正实数集合R+。

2) 参数:车次i在车站j的计划到站时分Ai,j及发车时分Di,j;最小追踪间隔Ih;最小发到间隔Ip;最小折返间隔It;正常列车最小停站时分wn;限速列车最小停站时分wd;车次i因在区间切换RM模式而产生的附加时分td1,i;车次i因在车站切换RM模式而产生的附加时分td2,i;ZC故障发生时刻ts;ZC故障预计持续时间tc;折返站k;车站j与车站j+1之间控制策略c对应的站间运行时分rc,j,j+1;车次i出清车站j的附加时分ti,j;限速运行下列车在车站j与j+1之间的最短运行时分Rj,j+1。

3) 决策变量:车次i在车站j的实际到站时分ai,j;车次i在车站j的实际发车时分di,j;车次i在车站j出发时是否选择第c条运行控制策略的判断变量yc,i,j。

1.3 约束条件

1.3.1 列车运行间隔约束

列车运行间隔的设定需考虑列车追踪间隔、发到间隔及折返间隔,相应约束条件如下:

ai,j-ai-1,j≥Ih,∀i,i-1∈N,j∈S

(1)

di,j-di-1,j≥Ih,∀i,i-1∈N,j∈S

(2)

ai,j-di-1,j≥Ip,∀i,i-1∈N,j∈S

(3)

ai,k+1-di-1,k≥It,∀i,i-1∈N

(4)

列车限速运行时,其安全防护距离会发生变化。根据上海轨道交通行车作业规定,当切除ATP(列车自动防护)运行时,列车与前车的安全防护距离不小于“一站一区间”。列车以RM模式运行时,需同时满足ZC故障已发生且故障未恢复以及列车处于ZC故障区域运行的条件。此时,对于i∈N,j∈Sd,当di,j大于ts且小于ts+tc时有:

di,j≥di-1,j+2+ti-1,j+2

(5)

1.3.2 停站时分约束

列车正常运行时,停站时分应不小于相应的正常列车最小停站时分,即有:

di,j-ai,j≥wn,∀i∈N,j∈Si

(6)

处于RM模式运行时,列车车站作业时间较正常情况更长,需对停站时分附加限制。对于i∈N,j∈Sd,当di,j大于ts且小于ts+tc时有:

di,j-ai,j≥wd

(7)

1.3.3 站间运行时分约束

列车正常运行时,列车站间运行时分与相应的列车速度控制策略有关。对于i∈N,j和j+1∈SSd,以及对于i∈N,j和j+1∈Sd,且di,j大于ts+tc时有:

(8)

(9)

列车限速运行时,其站间运行时分通常较正常情况更大。相应地,对于i∈N,j和j+1∈Sd,当di,j大于ts且小于ts+tc时有:

ai,j+1-di,j≥Rj,j+1

(10)

1.3.4 驾驶模式切换相关约束

列车驾驶等级降低需附加一定的过程时间消耗,而驾驶等级升级可快速完成,其过程时间消耗可忽略不计。当ZC故障发生时列车i处于故障区域,需先停车降级,再起动运行。即对于i∈N,j和j-1∈Sd,若列车i到达前方车站j的计划时刻Ai,j大于ts,且列车已离开车站j-1(即Di,j-1

ai,j≥Ai,j+td1,i

(11)

当故障发生时列车i正在车站j且前方为故障区域,列车i在车站j降级。即对于i∈N,j∈Sd,若列车到达车站j的计划时刻Ai,j小于ts,且列车离开车站j的计划时刻Di,j-1大于ts,则有:

di,j≥Di,j+td2,i

(12)

1.3.5 其他约束

为保障列车运行秩序,要求所有待调整列车到发时刻不早于相应的计划到发时刻,则有:

ai,j≥Ai,j,∀i∈N,j∈S

(13)

di,j≥Di,j,∀i∈N,j∈S

(14)

同时,对于i∈N,j∈S,当Di,j或者Ai,j小于ts时,应有:

ai,j=Ai,j

(15)

di,j=Di,j

(16)

此外,决策变量属性分别为:

ai,j,di,j∈R+,∀i∈N,j∈S

(17)

yc,i,j∈{0,1},∀c∈Cj,i∈N,j∈S

(18)

1.4 目标函数

延误时间是城市轨道交通运营管理中的重要考核指标。结合式(13)和式(14),以列车总延误时间尽可能小为优化目标[1-2],目标函数f为:

(19)

2 算法设计

上述约束条件为非线性混合整数规划模型,含多个if-then项,如式(4)、式(6)和式(9)。可对非线性约束条件作线性化处理,进而借助Cplex、Gurobi以及Lingo等数学规划求解器对线性化后的模型进行求解[7],也可运用遗传算法、粒子群算法等[1-4]对线性化后的模型进行求解。由于信号系统属于安全苛求系统,为保障列车运行安全与效率,结合问题特征,设计启发式算法进行求解,具体步骤如下:

步骤1:整理待调整列车车次数据、ZC故障区域及速度控制策略信息,并令i=1。

步骤2:判断车次i是否受影响。ZC故障发生时,在故障区域或未驶入故障区域的列车均需调整。若车次i受影响,则进入步骤3;否则,转步骤10。

步骤3:判断ZC故障发生时车次i是否位于故障区域。若车次i位于故障区域,则由所处位置对应的发车车站(记为起始调整站si)开始调整。若未驶入故障区域,则判断其运行线与前车是否满足正常运行间隔要求。若不满足,则由不满足正常运行间隔要求的第一个车站的后方车站(记此类车站为起始调整站si,如车站3不满足运行间隔要求,起始调整站为车站2)开始调整;否则,车次i运行线不需要调整,转步骤10。

步骤4:确定车次i在车站j(j=si)的调整出发时刻di,j。若ZC故障发生时,车次i位于故障区域内车站,则对出发时刻增加附加值;车次i位于区间或非故障区域内车站,则出发时刻直接取计划时刻。

步骤5:根据di,j判断车次i驶离车站j后所采取的运行策略。若ts≤di,j

步骤6:根据限速运行策略和站间运行时分附加条件(故障发生时,车次i恰好位于ZC故障区域内站间区间)确定ai,j+1。若ai,j+1满足限速运行间隔要求,进入步骤8;否则,维持站间运行时分不变,增大di,j使之恰好满足运行间隔要求后进入步骤8。

步骤7:按照由快到慢的顺序依次调整车次i在前方站区间的速度控制策略,使ai,j+1尽可能满足与前车的运行间隔要求。若使用最慢策略,ai,j+1依旧无法满足运行间隔要求,则使用最慢的策略,增大di,j使之恰好满足运行间隔要求后进入步骤8。

步骤8:比较ai,j+1与计划时刻Ai,j+1以及判断当前调整位置是否已超出故障区域。若不满足ai,j+1≤Ai,j+1且j+1>max(Sd)的判断条件,根据ai,j+1和车站j+1所处条件对di,j+1确定尽可能小的初始值,转步骤9。否则,维持站间运行时间不变,增大di,j使ai,j+1=Ai,j+1,车次i运行线调整结束,转步骤10。

步骤9:判断车次i运行线是否调整结束。若j+1=max(S),则车次i运行线调整结束,转步骤10。否则,令j=j+1,返回步骤5。

步骤10:判断是否结束调整。若i等于待调整车次总数,结束;否则,令i=i+1,返回步骤2。

3 算例分析

3.1 算例描述

仿真线路包含车站20座,按上行方向分别编号为S1至S20。假设上午7:50发生ZC故障,预计持续时间为10 min;故障期间列车在车站S6至S9之间以RM模式限速运行。

计划追踪间隔为180 s,最小追踪间隔为120 s,最小发到间隔为80 s。所有车站最小停站时分为30 s,RM模式下为35 s。各站区间列车均有5条不同等级的目标速度曲线,分别对应不同的站间运行时分。受影响车站S6、S7和S8的正常停站时分均为30 s,站间区间S6至S7、S7至S8、S8至S9的RM模式站间运行时间分别为186 s、182 s和205 s,计划运行时间分别为83 s、81 s和93 s。

所设计启发式算法通过MATLAB编程实现,便携式计算设备配置为Windows 10系统,32G内存,I7-10750H处理器。为分析算法计算效率,参考文献[7]采用大M法(M为适当大的正数,本文取5×105)将if-then非线性项进行线性化,并使用本文相同算例调用Gurobi规划器对线性化后的模型进行求解,运算终止条件设置上下界Gap(即上界与下界之间的差距)为0.1%。

3.2 算例结果与分析

分别用本文算法及Gurobi规划器对上述算例进行运算,得到列车运行调整方案如图2所示。由图2可见,基于本文算法运算得到的列车运行调整方案与调用Gurobi规划器运算得到的列车运行调整方案,两者的重合度较高。

图2 列车运行调整方案比较

图2的对应调整指令可由信号系统采集后自动下发并执行,也可由调度员设置后指挥列车运行。例如,车次3(从左至右第3条运行线)在区间切换RM模式限速运行至S8站;车次4在S6站扣车至车次3驶离S8站,并切换RM模式后运行至S7站;车次5在S5站扣车110 s后出发;车次3在S9站出发时按最快运行等级(等级1)运行。

基于求解时间、总晚点列次、终到站最大晚点时间及终到站总晚点时间四项统计指标,对本文算法及Gurobi规划器的计算结果进行对比,结果如表1所示。

表1 两种算法计算结果对比

由表1可见:在计算效率方面,Gurobi规划器求解时间较短(0.585 s),但本文算法仍能大幅缩短求解时间(2.263 ms),本文算法求解时间仅为Gurobi规划器的0.387%;考察终到站总晚点时间、终到站最大晚点时间以及总晚点列次(参考《上海轨道交通运营指标计算与统计标准》(Q/SD-XXZ-FB-XX-1514—2017),按终到站晚点时间大于2 min统计)等指标,两者计算结果均十分接近。此外,本文算法对应的目标函数值f为52 539 s,Gurobi规划器计算结果为52 416 s,即本文算法所得结果较最优解仅多了0.235%。算例运算结果表明,本文算法计算精度较好、效率更高,可作为全过程调整方案求解工具。

4 结语

城市轨道交通运营易受不确定因素影响。针对因ZC故障导致列车限速运行场景,结合列车运行速度控制策略,设计了考虑故障全过程的列车运行调整模型与启发式算法,并对具体算例进行仿真分析,得出以下结论:

1) 通过将列车运行安全防护因素纳入约束条件,可得到满足复杂运营需求的列车运行全过程调整方案;

2) 算例运算结果显示所设计的启发式算法能够在毫秒级得到近似最优方案,其目标函数值与Gurobi规划器的结果也十分接近;

3) 本文模型与算法可为调度员快速提供调整决策量化分析结果,并支撑信号系统新增功能开发。

未来可针对城市轨道交通其他故障场景或结合客流组织开展列车运行全过程调整方法研究。