基于城市轨道交通指标与城市特征的二维城市分类模型*

何鸿杰 陈先龙 马小毅

(广州市交通规划研究院有限公司,510030,广州∥第一作者,工程师)

由于城市轨道交通线网建设成本高昂,且线网建成后基本不存在调整的可能性,因此在实施建设前,需根据城市的社会经济发展状况和已建成的城市轨道交通系统现状,分析城市定位和城市轨道交通发展特征,进而判断城市轨道交通建设的迫切性和合理规模。对此,可充分利用既有通车城市的状况来预判待建设城市轨道交通线路的合理规模和开通后客流状况。

目前同城市定位和分类有关的研究方向主要有:基于城市职能和基于城市表现对城市进行分类,分别依据城市自身社会经济功能和社会经济属性水平对城市进行分类[1-2]。现状城市分类研究的主要对象集中在单独省份、城市群和社会经济联系较强城市集群,对不同省份单独城市分类的相关研究有限[3-5]。分类选用指标主要集中在社会经济数据,如常住人口、地区生产总值及三产产值等宏观数据[6]。常用的量化分类方法主要包括回归分析、聚类分析及神经网络等方法[7]。

综上,针对基于城市轨道交通相关指标和城市特征关系的城市分类方法、提供规划建设参照对象和参考值方法缺失的问题,本文建立一种二维城市分类模型,分别从城市总体特征和城市轨道交通发展特征两个维度对城市进行分类,并计算分数,进而对分类中的城市进行排序;基于分类结果,还可使用多元线性回归建立参照系,为未开通城市轨道交通线路的城市(以下简称“未通车城市”)提供预测和参考依据。

1 二维城市分类模型

1.1 二维城市分类模型的构建

两种维度指已开通城市轨道交通线路的城市(以下简称“已通车城市”)的总体特征(以下简称 “总体特征”)和城市轨道交通发展特征(以下简称“发展特征”)。总体特征是指包含社会经济发展水平和城市轨道交通运营状况在内的,某一时间节点的城市综合状态;发展特征指在一段时期内的城市轨道交通发展趋势。

二维城市分类模型的结构框架如图1所示。由图1可见,二维城市分类模型包含总体特征分类子模型和发展特征分类子模型。设j为年份编号,J表示研究时期内年份总数,g表示总体特征分类编号,b表示发展特征分类编号,根据两种子模型的输入指标,对多个已通车城市进行分类,获得如图2所示的分类结果。由图2可见,在研究时期内,g会逐年变化,而b在该时期内不变。

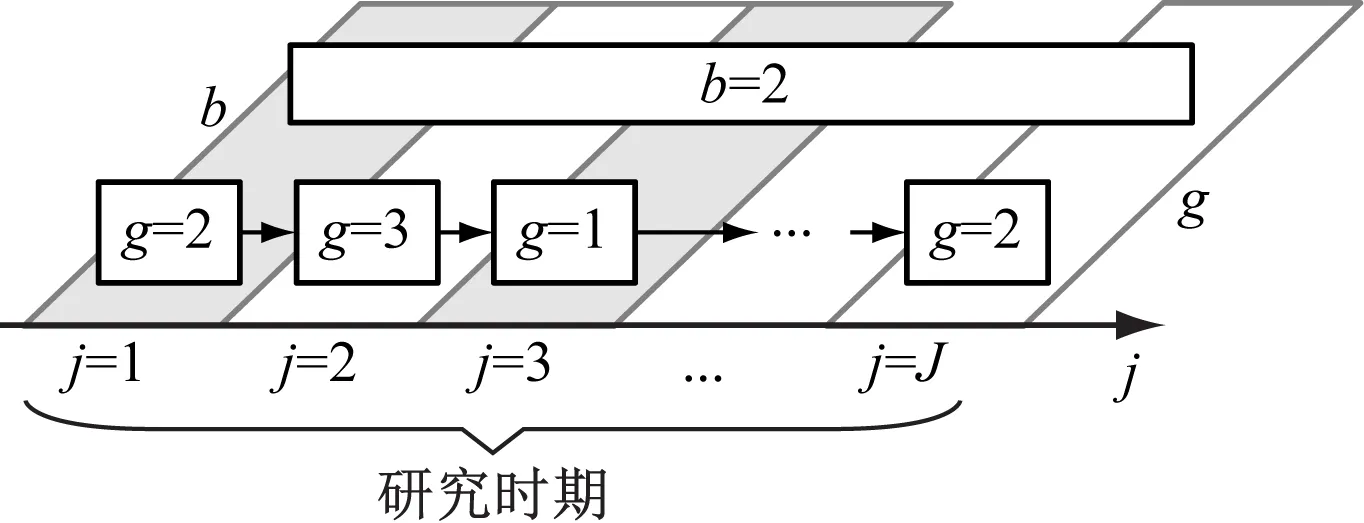
图2 某城市研究时期内不同时间点获得的两种分类特征

1.2 总体特征分类子模型

该模型的目标是根据给定的社会经济发展水平指标(以下简称“社会经济指标”)与城市轨道交通运营指标(以下简称“城轨指标”),对城市进行分类,并赋予总体特征。该模型的主要处理流程包括特征信息提取、聚类分析和分类分数计算。

1.3 发展特征分类子模型

该模型的目标是根据城轨指标,分析不同城市的客流和运营发展趋势,构造差异度函数,完成分类并赋予发展特征。该模型的主要处理流程包括特征信息提取、构造差异度矩阵、聚类分析和分类分数计算。

1.4 基于分类结果的多元线性回归

总体特征分类子模型和发展特征分类子模型完成分类和分类分数计算后,还需采用多元线性回归方法,基于分类结果建立主要城轨指标(因变量)和社会经济指标(自变量)的关系式,为未通车城市提供预测参考。第一个子模型的因变量选取基于载荷矩阵和主因子方差贡献率,第二个子模型的因变量选取基于权重均值,两者自变量的选取均基于多元线性回归的拟合优度。

2 数据基础和指标选用

2.1 数据来源和指标选取

本文研究范围限定在2014—2019年间我国已通车的城市。根据2014—2019年中国城市轨道交通协会发布的《城市轨道交通统计和分析报告》和住房和城乡建设部发布的《城乡建设统计年鉴》,得到城轨指标如表1所示。根据2014—2019年我国经济社会大数据研究平台收录的各省市年度统计年鉴、《城乡建设统计年鉴》和《中国城市统计年鉴》,得到社会经济指标如表2所示。总体特征分类子模型会使用社会经济指标和城轨指标,而发展特征分类子模型仅使用城轨指标。社会经济指标和城轨指标的数据均由城市、年份和指标3个维度构成,例如北京2019年的常住人口总量为2 190.1万人。

表1 城轨指标及内容

表2 社会经济发展特征指标及内容

2.2 数据预处理

由于不同指标的单位或数量级不同,在进行聚类分析时,数量级较大的指标对结果会产生较大影响,因此需要预处理消除指标间数量级的差异。同一指标的数据不一定符合正态分布,为保留原始数据的分布特征,采用PCA(主成分分析)法提取特征信息,并对数据进行量纲一化预处理。

当数据缺失时,判断数据是否为0(例如未通车城市的城市轨道交通客运量为0):如果是则填充0,否则使用线性插值法填充数据。

3 分类模型构建

3.1 总体特征分类子模型

3.1.1 模型输入

城市i在年份j的社会经济发展数据和城市轨道交通运营数据分别用向量Sij=[sij1sij2…sijU]T和Rij=[rij1rij2…rijV]T表示。其中:siju表示城市i在年份j的第u个社会经济指标,u= 1,2,…,U;rijv表示城市i在年份j的第v个城轨指标,v= 1,2,…,V。

将向量Sij和Rij进行组合,得到城市i在年份j所有指标向量Aij=Sij∪Rij=[aij1aij2…aij(U+V)]T,其中aijw表示城市i在年份j的第w个指标,w= 1,2,…,U+V。

设城市总数为N,该模型将年份j对应的Nj(Nj≤N)个已通车城市之Aij作为模型输入。

使用模型进行分类后,得到年份j的第g类城市编号集合CAll,gj,其中CAll,gj中存放对应分类的城市编号,GAll为分类数量,g=1,2,…,GAll。

3.1.2 数据预处理

该模型采取量纲一化方法进行数据预处理:

(1)

式中:

aP,ijw——经过量纲一化处理后,城市i在年份j的指标w。

3.1.3 特征信息提取

先使用PCA法处理量纲一化数据,再根据累计方差贡献率阈值δ筛选主因子。设最佳主因子数量为λ,载荷矩阵为Xj,维度为λ×(U+V),它的元素xqwj表示年份j指标w在主因子q坐标轴上的投影;主因子方差贡献率向量为αj=[α1jα2j…αλj],αqj表示年份j主因子q的方差贡献率。λ的选取流程如下:

步骤1:将主因子根据αqj从大到小进行排序;同时计算累计方差贡献率,当累计方差贡献率略微大于或等于δ时,参与方差贡献率累计的主因子数量即为最佳主因子数量λ1。

步骤2:以区间[1,U+V]作为变化范围,使用交叉验证法计算不同主因子数量下使用PCA的重构误差,误差最小的主因子数即为最佳主因子数量λ2。

步骤3:确定λ=max(λ1,λ2)。

确定λ后,将筛选的主因子指标值作为ICA(因子分析)的输入,使用ICA法将主因子指标转化为独立分量,以在聚类分析前尽可能消除主因子之间的相关性,其中主因子的数量等于独立分量的数量。

3.1.4 聚类分析

聚类分析采用层次聚类(Ward准则)方法。最佳城市分类数量通过使用CVI(聚类有效性指标)评估不同分类数量下的分类质量确定。该聚类分析过程属于无监督学习过程,没有真实分类结果作为校核参考,故CVI应不要求真实分类结果。符合这一要求的CVI有Calinski Harabasz指标、轮廓系数、Davies Bouldin指数和Dunn指数等。这些CVI曲线的局部极值点或肘部即为最佳分类数量。

3.1.5 分类分数计算

分类分数的计算基于Xj和αj,其中Xj表示主因子和原始指标的投影关系,αj表示主因子重要度。在计算分类分数前,需要提前计算城市i在年份j的城市分数zAll,ij:

(2)

在此基础上进一步计算总体特征分类g在年份j的分类分数yAll,gj:

(3)

3.1.6 多元线性回归

αj和Xj相乘获得不同城轨指标的权重向量,从向量中选取权重最大的城轨指标作为因变量。使用AIC准则(Akaike Information Criterion)来评价拟合优度,使多元线性回归从自变量中提取尽可能多信息的同时,减少自变量的个数。自变量仅从社会经济指标中选取,计算不同自变量组合下的AIC值EAI,EAI最低的组合即为最佳自变量组合。EAI为:

EAI=2k+GAllln(ESS/GAll)

(4)

式中:

k——自变量个数;

ESS——回归预测值和实际值的残差平方和。

3.2 轨道交通发展特征分类子模型

3.2.1 模型输入

构造三维张量M作为该分类模型的输入,维度为N×J×V,其中它的元素为rijv。

根据输入数据构造表示不同城市间客流发展趋势区别的差异度矩阵。之后,与总体特征分类子模型中的过程类似,使用聚类分析得到第b类城市编号集合CRail,b,其中CRail,b中存放对应发展特征分类的城市编号,GRail为分类数量,b=1,2,…,GRail。

3.2.2 数据预处理

该模型采取量纲一化方法进行数据预处理:

(5)

式中:

rP,ijv——量纲一化处理后城市i的第v个城轨指标。

3.2.3 特征信息提取

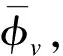
设θ为指标权重阈值,重要指标选取流程如下:

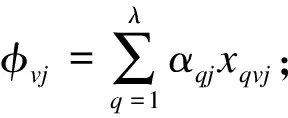
(6)

3.2.4 聚类分析

与城市总体特征分类子模型直接利用ICA输出的独立分量计算城市间差异不同,该子模型在使用层次聚类(Ward准则)进行城市分类前,需构造二维差异度矩阵D={dih|i,h=1,2,…,N},其中:

(7)

式中:

dih——城市i和城市h间的差异程度,包括指标大小差异和趋势差异。

D构造完成后,聚类算法将其作为依据和输入进行城市分类。

3.2.5 分类分数计算

计算城市i的城市分数zRail,i,即:

(8)

则分类b的分类分数yRail,b为:

(9)

3.2.6 多元线性回归

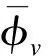
4 计算实例

4.1 总体特征分类

4.1.1 特征信息提取

以2014—2019年为研究期,使用PCA对所有指标进行分析。取δ=0.95,各年份选取的主因子数量均为4,则研究期内各主因子方差贡献率和累计方差贡献率如图3所示。

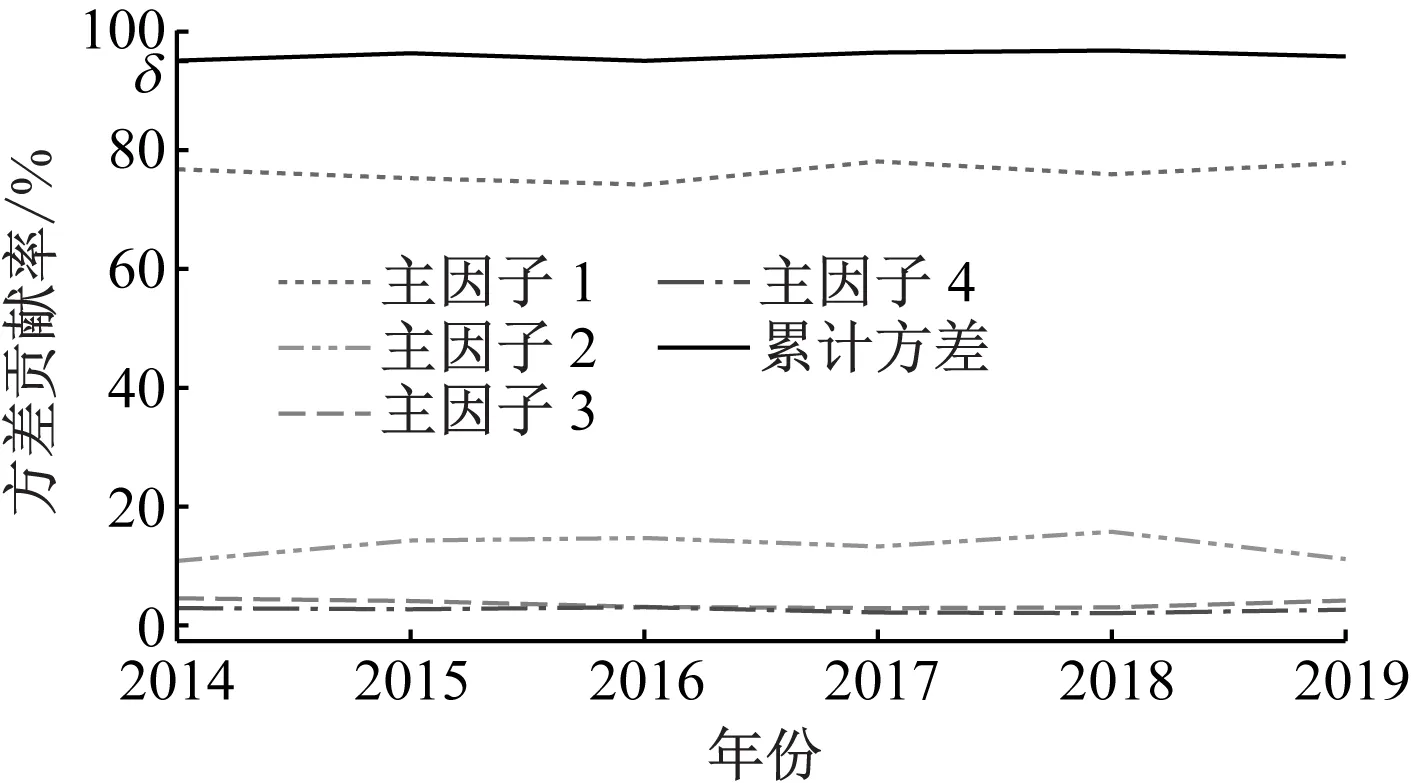
图3 研究期内的主因子方差贡献率及累计方差贡献率变化

表3为研究期内的指标主因子情况;显示了2014—2019年贡献率最大的主因子和部分原始指标的投影关系。由表3可见:投影较大的指标主要集中在城轨指标,说明城轨指标对城市总体特征的影响较大;各年投影较大的指标均比较稳定,特别是指标A1—A4、B1—B5、C4、D1、D3和D5在所有年份中均有出现。

表3 研究期内的指标主因子情况

4.1.2 聚类分析和分类分数计算

以2019年为例,划分已通车城市的总体特征分类。最佳分类数量在区间[3,12]范围内取值,不同分类数量的CVI变化曲线如图4所示。不同年份部分城市所属分类和分类分数变化如图5所示。

a) 轮廓系数(正相关)

可以明显看出,当分类数设置为8时,Davies Bouldin指数和Dunn指数出现极值,而轮廓系数则出现肘部,由此可以判断最佳分类数量为8。

2019年总体特征聚类分析结果和表3中部分投影较大指标的组内均值如表4所示,其中分类排名根据分类分数排序得到。排名靠前的城市,社会经济发展水平在国内处于较高水平,轨道交通系统的发展趋于成熟。排名靠后的城市,城市轨道线网规模较小,客流强度相对较低。

表4 2019年总体特征聚类分析结果和部分指标的分类内均值

从图5看出,部分城市所属分类和对应分数不断变化,总体特征和城市间的差异也会随之改变。因此未通车城市根据参照系获得合理线网规模、预测客流强度时,应参考位于最新时间节点的参照系。如果需要参考一段时期内的规模和客流的变化趋势,则要利用发展特征分类子模型的计算结果,以建立第二种参照系。

4.1.3 多元线性回归结果

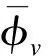
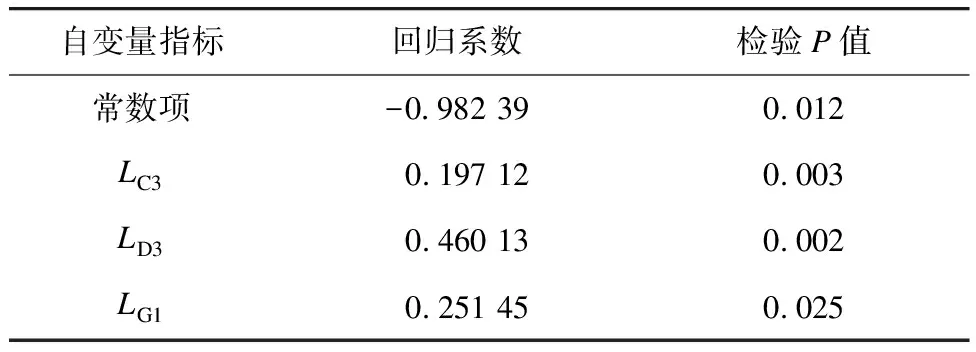
表5 基于2019年总体特征分类的自变量指标选取与多元线性回归结果

由表5可知,基于分类的回归分析比直接使用原始数据更优,分类后的拟合优度得到大幅提高,基于分类的回归分析EAI(越小越好)和决定系数R2(越大越好)分别为3.27和0.890,直接基于城市的回归分析则分别为16.34和0.558,前者远优于后者。此外,客运强度同人口密度、第三产业增加值及小客车保有量正相关,基本符合现实情况。

选用部分城市轨道交通线网在建或社会经济水平较高的城市作为计算实例,使用上述回归方程预测其客运强度,结果如表6所示。由表6可见:唐山和烟台的预测客运强度为负数,说明按照唐山和烟台目前的社会经济发展程度暂未达到建设城市轨道交通的水平;尽管泉州和嘉兴的预测客运强度均大于0,但是非常小,说明城市轨道交通系统建成后的客流效益有限;南通的预测客运强度较大,建设的必要性相对较大。

表6 未通车城市的总体特征预测值

4.2 发展特征分类

4.2.1 特征信息提取

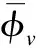
表7 城轨指标的及选取判断结果

4.2.2 聚类分析和分类分数计算

对已通车城市的发展特征进行分类,最佳分类数量的确定方法与总体特征分类子模型相同,使用CVI对聚类结果进行评估,最佳分类数量为7,分类结果和研究时期内部分重要指标的组内均值如表8所示。与总体特征分类子模型类似,基于分类的回归分析拟合效果优于直接基于城市,前者EAI和R2分别为-8.72和0.985,后者分别为21.08和0.637。

表8 基于发展特征分类的自变量指标选取与多元线性回归结果

表9所示分类排名根据分类分数计算和排序得到,与总体特征不同,发展特征反映一段时期内的轨道交通发展趋势。排名靠前的城市,线网规模、建设速度、客流指标均处于较高水平。排名靠后的城市,城市人口规模较小,客运强度和线网规模保持在相对较低水平且增长速度缓慢,既有轨道交通设施已经能充分满足现状城市轨道交通出行需求。

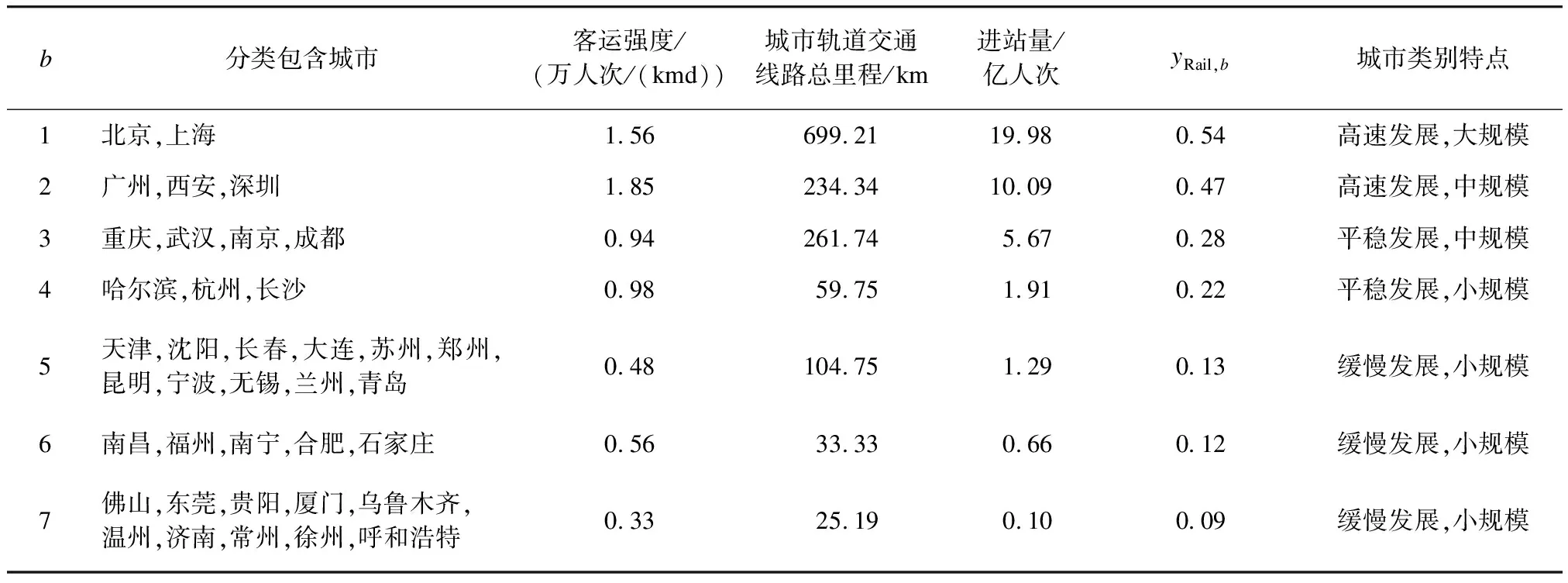
表9 研究时期内发展特征聚类分析结果和部分指标的分类内均值

4.2.3 多元线性回归结果

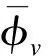
以表6的城市为例,使用回归方程计算其在研究时期内的城轨指标平均水平,结果如表10所示。泉州和唐山的客运强度预测值均为负值,烟台和嘉兴的预测值接近0,这些城市建设城市轨道交通后的客流效益发展较慢,建设城市轨道交通的迫切性不足。南通的社会经济发展水平和城市建设速度提升显著,远大于其他4个城市,建设城市轨道交通的必要性相对较高。

表10 未通车城市的发展特征预测值

5 结语

本文基于主成分分析、因子分析和聚类分析提出了二维城市分类框架,提取城市的总体特征和发展特征,并进行分类,从两个角度对城市进行评价和定位。此外,还提出了针对上述两种分类的分类分数计算方法,用于分类间等级排序。基于分类结果进行多元线性回归,得到预测重要城轨指标的回归方程;利用社会发展经济指标为未通车城市提供指标预测值,进而判断在未通车城市建设城市轨道交通系统的必要性和迫切性。