基于无限元法的离心泵空化辐射噪声指向性研究
葛秉鑫张林华宋守杰张惟斌宋永兴
(1.山东建筑大学热能工程学院,山东 济南 250101; 2.流体及动力机械教育部重点实验室(西华大学),四川 成都 610039)
0 引言
离心泵作为能量转换和流体输送的重要机械设备[1],不仅普遍应用于农业灌溉、石油化工、水利工程等领域,还在远洋船舶、潜艇作业、航空航天等前沿科技领域发挥着至关重要的作用。 然而,由于离心泵内部流场构造复杂,在运行过程中往往伴随着剧烈的振动和噪声[2]。
离心泵产生的噪声通常通过蜗壳向外辐射,或通过所连接管道中的介质向上、下传播。 其噪声主要分为机械结构振动噪声和流体流动噪声。 振动噪声往往是由各个部件存在制造公差和旋转部件不对中引起的机械结构振动导致的。 随着加工精度的不断提升,离心泵的机械振动引起的噪声问题可以很好地解决,而流体流动诱发的噪声已逐渐成为离心泵噪声声源的主要类型。 流体流动产生噪声的主要原因有湍流、流动分离、内部空化、水锤以及流固耦合等[3-4]。 随着更高速、大功率离心泵的发展,噪声问题变得越来越严重。 因此,研究离心泵流动产生的辐射噪声特性具有重要的实际应用价值。
DURRER 等[5]指出离心泵噪声主要是流体流动引起的,并认为采用流体压力脉动的频谱分析方法可以更好地分析离心泵辐射噪声;JIANG 等[6]运用流固耦合的边界元方法,模拟并分析了多级离心泵流体流动诱导的结构振动与噪声;谈明高等[7]运用声振耦合方法研究了叶片数量对离心泵蜗壳所产生的辐射噪声的影响;董沛鑫等[8]利用声学边界元方法研究了以离心泵蜗壳为主要声源的辐射噪声与叶轮转速之间的响应关系;郭荣等[9]应用高阶Bezier 曲线法控制叶片型线,分析了不同叶片型线对离心泵辐射噪声的影响;张俊杰等[10]利用振动特性实验法测试了离心泵在正常运转时的振动和噪声,分析了离心泵辐射噪声的起因和改善措施;程效锐等[11]运用Lighthill 声类比理论研究了叶片尾缘上不同的开缝位置和宽度对离心泵辐射噪声的影响;李仁年等[12]运用边界元方法模拟并分析了蜗壳隔舌在不同时序位置时离心泵辐射噪声的变化规律。
综上所述,运用边界元方法针对离心泵流动诱导噪声的影响因素做了很多研究,但未见采用声学无限元法对离心泵空化时外声场辐射噪声的指向性分布进行深入分析的研究。 文章以Realizablek - ε湍流模型、Zwart-Gerber-Belamri(ZGB)空化模型数值模拟了离心泵的流场,利用Lighthill 声类比理论提取离心泵基于体积和基于表面的空气动力源项,采用声学有限元、无限元相结合的声振耦合方法求解并分析离心泵外声场辐射噪声的指向性分布。
1 数值模型理论
1.1 湍流模型
在离心泵内部流场的瞬态计算中,湍流模型采用Realizablek -ε模型[13-14],与标准k -ε湍流模型相比较,更加适用于离心泵内部的旋转流动。
湍流动能方程(k方程)、能量耗散率方程(ε方程)分别由式(1)和(2)表示为
式中ρ为密度,kg/m3;k为湍动能,m2/s2;uj为流体速度,m/s;ε为湍流脉动速率,%;C1、C2为固定常数;σk和σε分别为k方程和ε方程的湍流普朗特数;Pk为层流速度梯度产生的湍动能,m2/s2;Gb为浮力产生的湍动能,m2/s2;YM为紊流扩散波动;v为湍流速度,m/s;μ为动力黏度,N•s/m2;μt为湍流动力黏度,N•s/m2;E为扩散率。
1.2 空化模型
通过ZGB 空化模型[15]计算空泡的产生和溃灭,考虑非冷凝性气体和湍流脉动的影响[16-17],假设空泡半径相同,当瞬时静压P小于饱和蒸气压Pv时,气泡膨胀的相变率Re由式(3)表示为
当P>Pv时,气泡压缩和破裂的相变率Rc由式(4)表示为
式中Ce、Cc分别为蒸发和凝结经验系数,取Ce=50、Cc=0.01;αnuc为成核点体积分数;αv为蒸汽体积分数;ρ1、ρv分别为流场密度、蒸气密度,kg/m3;RB为空泡半径,m。
1.3 Lighthill 声类比理论
声类比理论和Lighthill 方程是研究离心泵等旋转机械辐射噪声特性的基础,也是现代气动声学的起源[18-19]。 结合连续方程和动量方程,声学波动方程可以由式(5)表示为
由式(5)和纳维-斯托克斯(Navier-Stokes)方程可以推导出Lighthill 声类比理论方程,由式(6)表示为
式中c0为绝热时的声速,m/s;ρ′ =ρs- ρ0,为密度分量,ρs、ρ0分别为有声波和无声波的密度,kg/m3;Tij为Lighthill 应力张量。 式(6)的左侧是声学的波动方程,右侧是流体动力学引起的相互作用力,是声源项,其中Tij由式(7)表示为
式中ρμiμj表示雷诺应力,N;μi、μj分别为湍流正应力和湍流切应力,N;σij为黏性应力张量,N•s/m2;P和P0分别为有、 无声波时的压力,Pa。表示热传导,当i=j时,δij =1;当i≠j时,δij =0。
在低速的绝热流动中,σij远远小于ρμiμj,可以忽略不计,又因为过程绝热,所以有
由此可以推导出Lighthill 应力张量的近似方程Tij =ρμiμj。
1.4 声学无限元法
声学无限元法是一种利用声波在声源近场的分布来推算声源远场噪声声压的方法,用以模拟声源的自由声场辐射[20]。 其原理是在声源外部创建一个完全包裹声源的无反射边界面,声波可以通过无反射边界而不会发生反射,在边界内部为有限元计算域,以边界面网格为基底的外部为无限元计算域。由于无限元的基底是二维的面网格,且其所需要求解的方程矩阵是对称的稀疏矩阵,因此在求解运用边界元方法难以处理的大型复杂结构以及高频段声学计算问题时,运用无限元法求解速度更快且精度更高。
声学无限元法是基于Lighthill 声类比理论,结合Curle,s理论[21]进行的声场模拟。(1)用Curle,s理论中的体积分计算体声源;(2) 用Curle,s 理论中的面积分计算面声源;(3) 自由声扩散的Curle,s 函数作为声源计算的边界条件。
对式(8)在边界Ω 上进行积分,引入测试函数δρ,并在面积分上应用Tij,可推导出式(9)为
式中ρa、ρb分别为当地密度和环境密度,kg/m3; Ω为有限元计算域的单位体积分;Γ 为有限元表面;ni为Γ 表面的法向分量;δ为Γ 表面的总位移量,m;,可以计算出面声源;Tij项可以计算出体声源。
计算声源远场声压的公式是一个多阶次式,远场声压的强弱受声场在计算域中的位置及插值阶次影响,远场声压P(r) 计算由式(10)表示为
式中AN为有无反射边界对监测点声压的N阶贡献量,dB;r为监测点和无反射边界之间的距离,m。
插值的阶次可以用来估算无反射边界上节点的数目,节点数目越多对于远场声压的计算越精准,但计算量也随之增大。
2 计算参数及边界条件
2.1 结构参数及网格划分
运用CFturbo 软件设计并抽取离心泵流体域。整个离心泵的计算域分为进口段、叶轮、蜗壳等3 部分,三维模型如图1 所示,离心泵设计参数:叶片数为6,叶轮转速为2 880 r/min,叶轮出口宽度为6 mm,叶轮进口直径为38 mm,设计流量为4.5 m3/h,扬程为8 m。
图1 离心泵流体域三维模型示意图
对于抽取的离心泵流体域进行非结构网格划分,为了减小由于网格数量所导致的误差,在进行声辐射计算前进行了网格独立性验证[22],计算了4 组不同网格数量时的扬程值,结果见表1。 考虑到计算机的算力和计算精度,最终选取方案3,其流场网格如图2(a)所示。 在声学模拟软件中,对流场计算数据进行提取及转换,映射得到离心泵的外包络面,即声学网格,网格数量为199 762,如图2(b)所示。
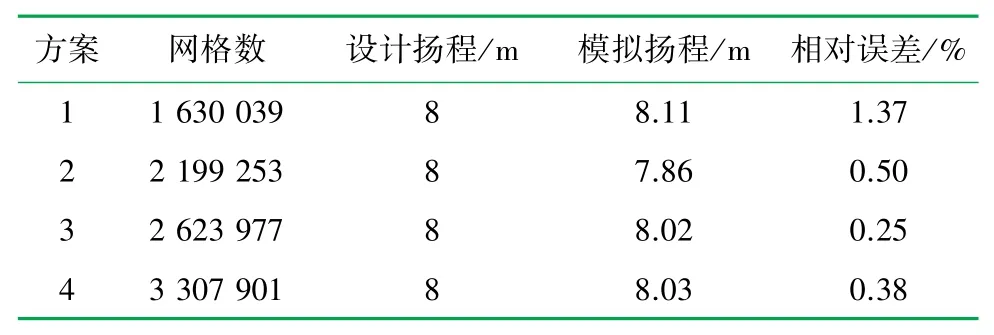
表1 网格独立性验证结果

图2 离心泵流场网格和声学网格示意图
2.2 流场计算参数
在流体模拟计算设置中,动静部件间使用瞬态交界面(Transient rotor/stator interface)进行数据交换,设置叶轮为旋转区域;湍流模型采用Rrealizablek -ε模型,空化模型采用ZGB 模型。 进口处设置为速度进口,其值为1.25 m/s,壁面温度为恒温300 K,出口处设置为自由压力出口;时间步长Δt设为5.78×10-5s(叶轮每转动1°),迭代次数为20 次,当流场表现出显著的周期性且周期性变化达到稳定之后,提取最后4 个旋转周期的数据进行声场计算。
2.3 声振耦合计算
利用Lighthill 声类比理论对流场计算的结果分别进行面声源和体声源的提取。 面声源主要包括离心泵表面振荡诱导噪声,对应着偶极子声源,体声源主要包括自由湍流诱导噪声,对应着四极子声源。采用傅里叶(Fourier)变换,将从离心泵流场计算中提取的时域数据转换为频域脉动信号,并将其插值到整个离心泵的外壁表面上,即声学网格上,作为声振耦合面。 在离心泵声学网格外100 mm 处创建完全包裹离心泵的无反射边界面,无反射边界内为有限元计算域,用以计算模拟近声场;无反射边界外为无限元计算域,进行自由声场辐射,用以模拟远场声辐射,如图3 所示。

图3 有限元与无限元计算模型示意图
3 结果及分析
3.1 流场计算结果分析
在流场表现出显著的周期性且周期性变化达到稳定之后,提取第10 个旋转周期的数据进行分析。此旋转周期内离心泵内部的空化分布以及蜗壳隔舌区域的空化分布如图4 所示。 可以看到,空化主要集中在转动到左侧的3 个叶片的前缘以及当叶片尾缘掠过蜗壳隔舌区域时的隔舌尖角处。 主要是因为隔舌区域设计的过于尖锐,叶片与隔舌之间空隙狭窄,随着叶片转动,从叶片掠过隔舌时,空泡开始初生,在随后的转动中,叶片前缘的空泡不断生长,直至溃灭。
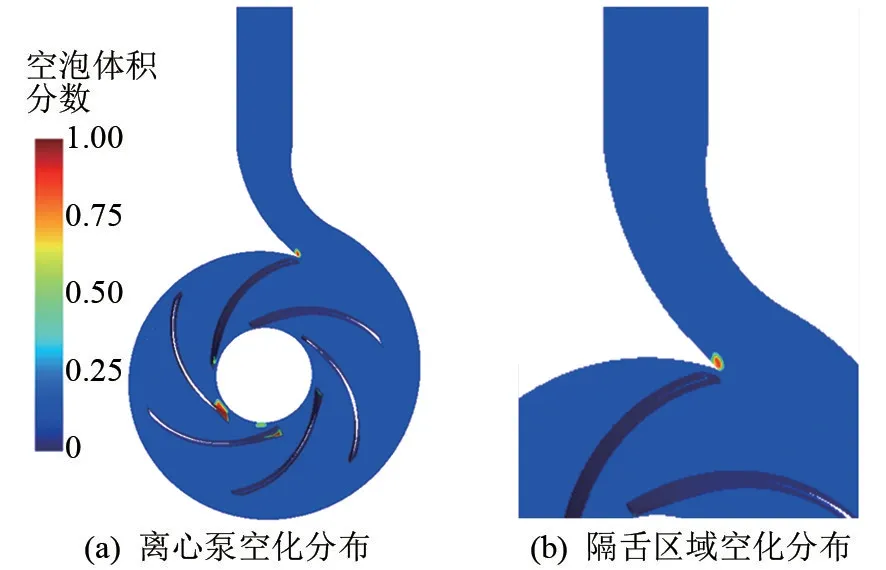
图4 叶片每转动10°时截面空泡分布
离心泵在该旋转周期内的压力分布云图如图5所示。 在隔舌夹角下侧的压力最大,左侧叶片的吸力面前缘压力最小,各个流道内压力分布呈现明显的差异性,隔舌右侧叶片吸力面的压力小于左侧叶片。 这是因为所设计的离心泵较小,叶片与蜗壳间的距离太过狭窄,尤其是蜗壳隔舌区域,导致各个流道内流动不均匀。
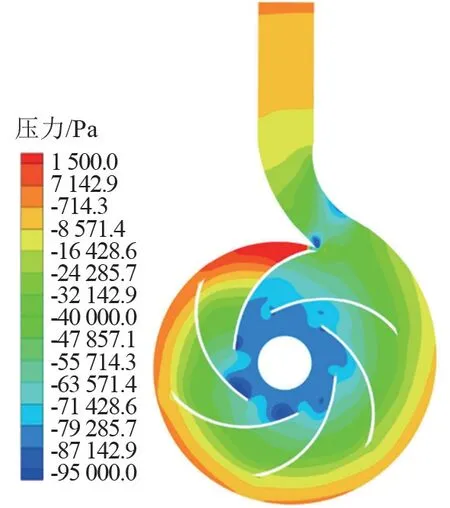
图5 压力分布云图
3.2 辐射声功率计算结果分析
以离心泵流场计算结果映射得到的结构振动响应作为声学边界条件,计算基于声振耦合办法的离心泵辐射噪声。 流场计算得到的时域数据经过Fourier 变换,其计算频率范围为fmin=10 Hz 和fmax=8 640 Hz,而频率分辨率Δf=10 Hz,频谱计权方式采用A 计权声级。 为了计算离心泵的辐射声功率谱,在离心泵外建立了符合标准ISO3744:2010[23]的场点网格,在运用无限元法进行远场噪声计算时,将计算结果输出到场点网格上,如图6 所示。
图6 场点布置图
离心泵的轴频(Axial Passing Frequency,APF)为48 Hz,叶频(Blade Passing Frequency,BPF)为6倍的APF,即288 Hz。 离心泵辐射声功率谱如图7所示,可以看出,离心泵的声辐射功率在轴频、叶频及其谐频处均呈现出一定的峰值,声功率谱随着频率的增大整体呈下降的趋向。 0~1 000 Hz 频段是整个计算频率范围内声功率最大的频段,且离心泵在轴频APF 处达到最大值108 dB,这是因为所设计的离心泵流道较为狭窄,流体在流道内流动时,具有一定的差异,导致在离心泵运行中,轴频是流动诱导噪声的主要频率。 声功率峰值不仅出现在APF、BPF 及其倍频,也出现在一些其他频率,如105、136、155、167 倍APF 等,在这些频率处也出现峰值。这可能是因为离心泵内空化初生、溃灭所造成的宽带噪声被轴频及其谐频所调制,导致部分特定高频声压级显著提高。 在4 000~4 200 Hz 频段,声辐射功率相较于其他频段更加的无规律,这是由于叶轮和蜗壳之间复杂干涉作用导致内部流场较为紊乱。
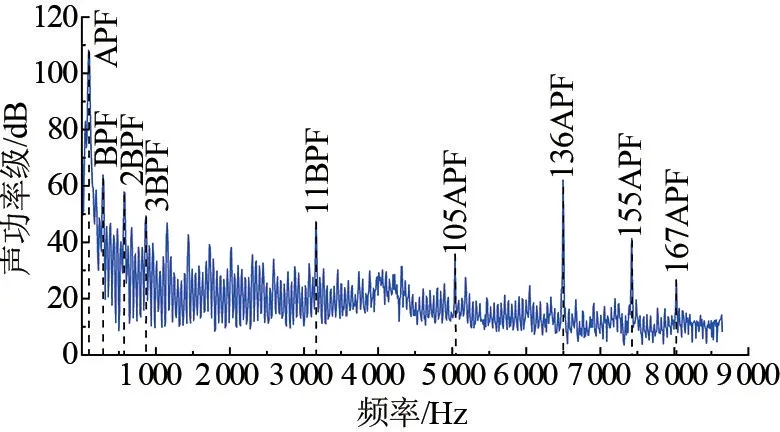
图7 离心泵辐射声功率谱
3.3 辐射噪声声压分布分析
为了获得离心泵辐射噪声声压级分布图,以离心泵的叶轮中心为圆心,在z=0 和x=0 截面分别创建一个半径为200 mm 的圆形面网格作为声压级检测区域,在运用无限元法求解离心泵外声场时,将计算结果映射到面网格上,其具体布置如图8 所示。
图8 离心泵外部声压检测区域布置
离心泵在APF、BPF、2BPF 时,在z=0 和x=0处的声压级分布分别如图9、10 所示。 从整体上看,距离离心泵中心越远,声压强度越小,且随着频率的增高而不断降低。 在叶轮周围声压分布中,叶轮左侧区域强于右侧区域,上侧区域强于下侧区域,前侧区域强于后侧区域,其中蜗壳隔舌区域噪声最为剧烈。 从图9(a)和图10(a)中可以看出,在APF 时辐射声场检测区域声压整体最强,整体约处于100 dB,这是因为所设计的离心泵流道较为狭窄,流体在流道内流动时,具有一定的差异,导致在离心泵运行中,轴频是流动诱导噪声的主要频率。 且在图9(a)中可以看到,叶轮前侧区域声压强度明显大于后侧区域以及z=0 剖面,这是因为离心泵的进口段与叶轮的交界面位于前侧区域,流体流入进口段,叶轮与进口段之间动静交界之间产生了大量低频噪声。 从图9(b)和图10(b)中可以看出,在BPF 时噪声主要集中在叶轮周围,随着叶轮转动,噪声不断向外辐射,其中又以叶轮的左侧区域、上侧区域以及蜗壳隔舌区域噪声最为强烈。 这是因为蜗壳隔舌太过尖锐,每当叶片掠过隔舌尖角,流场内产生了与该频率相关的涡旋,且在隔舌区域产生振荡也诱发了噪声,随着叶片带着涡旋继续向下转动,由于蜗壳内壁面平滑,涡旋随着转动逐渐变小直至消散,造成了从蜗壳隔舌处开始,噪声沿着蜗壳逆时针方向逐渐减小的现象。 从图9(c)和图10(c)中可以看出,在2BPF 时离心泵诱导的声压强度降低,辐射阶次较为均匀,只有蜗壳隔舌区域噪声略大于周围,这说明叶片掠过隔舌时产生的振荡所造成的噪声仍然存在,而产生的涡旋因为与该频率相关性低,所以噪声在离心泵周围呈现出均匀扩散的现象。
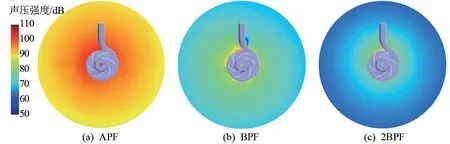
图9 APF、BPF、2BPF 处z=0 截面场点声压分布图
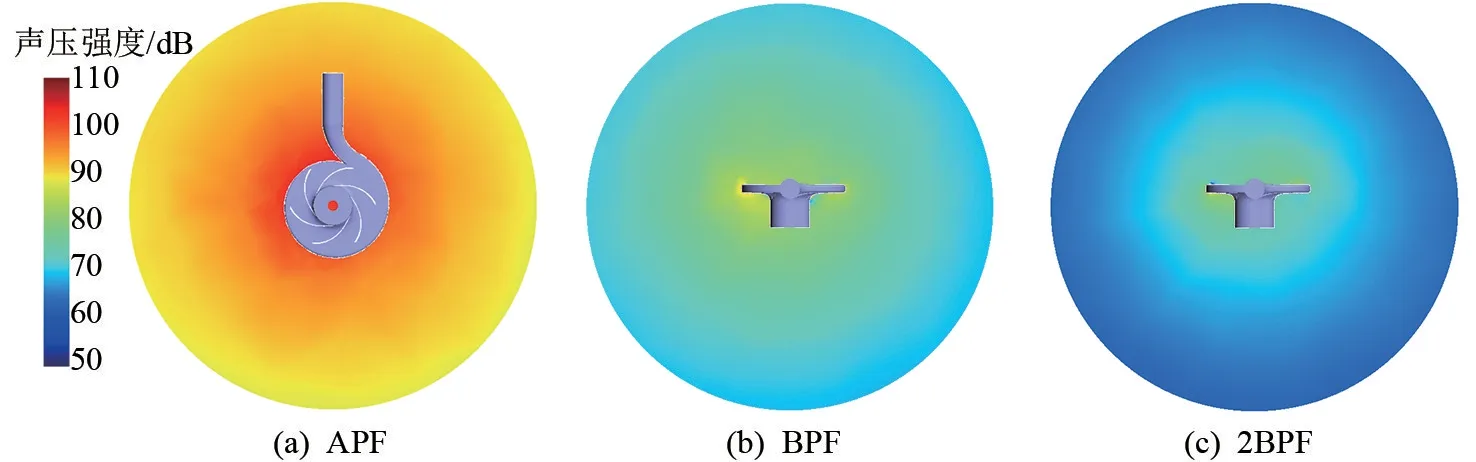
图10 APF、BPF、2BPF 处x=0 截面场点声压分布图
3.4 辐射噪声指向性分析
声波是球面波,所以声音在空气中传播有明显方向性。 在相对于声源的不同空间位置上,其声压级随着位置的不同而改变。 为了更精确的监测离心泵辐射噪声的指向性分布,设离心泵的叶轮中心O点为圆心,在距叶轮中心200 mm 的圆周上共设置36 个场点,在运用无限元法求解离心泵外声场时,将计算结果映射到各场点上。 定义水平向上为极坐标中的0°,沿顺时针方向为正方向,每个场点之间夹角为Δα=10°,如图11 所示。
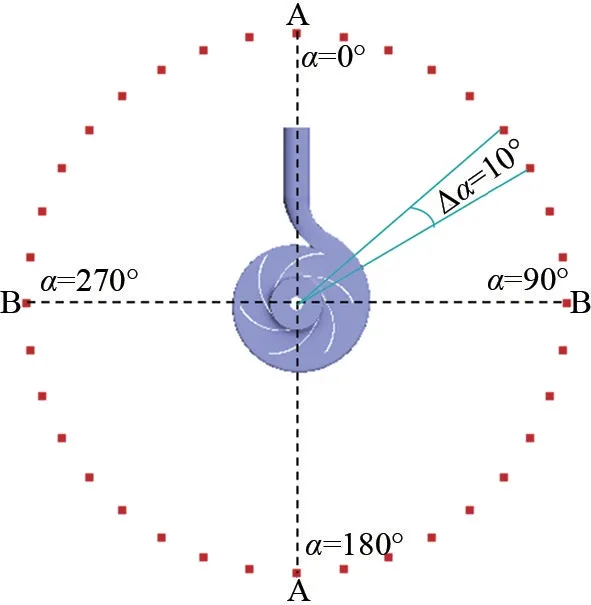
图11 离心泵外部指向性场点布置图
轴频、叶频及部分谐频下离心泵指向性声压分布如图12 所示。 从整体上看,随着频率不断增大,离心泵各个方向的声压强度呈现降低的趋向。 在不同的频带范围内,离心泵的辐射噪声具有不同的指向性分布。 这说明离心泵运行时产生的辐射噪声主要为低频噪声。
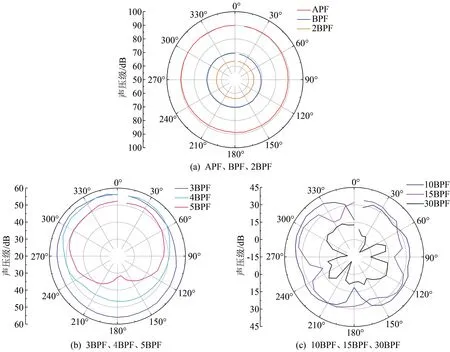
图12 轴频、叶频及部分谐频下离心泵指向性声压分布图
由图12(a)可知,在APF、BPF、2BPF 时,离心泵的指向性分布较为均匀,泵的B-B 上侧区域略大于B-B 下侧区域,A-A 左侧区域略大于A-A 右侧区域。 这说明在低频时,离心泵周向声压强度相对高频较大,且无明显的指向性。
由图12(b)和(c)可知,在3BPF 时,离心泵周向的声压分布也较为均匀,最大、最小指向性分布分别出现在320°和60°;在4BPF 时,B-B 上侧区域明显大于B-B 下侧区域;在5BPF 时,离心泵辐射噪声的指向性分布初具一定的偶极子分布,在0°区域声压级最大,在170°区域声压级最小,此时声压指向性从均匀分布向偶极子分布转变。 由图12 可知,在10BPF 时,其指向性的偶极子分布更加明显,在330°区域声压级最大,在180°区域声压级最小,这说明5BPF 至10BPF 的频段内,离心泵的指向性分布主要受离心泵非定常流动诱导的叶轮叶片表面、蜗壳壁面振荡产生的偶极子声源影响,导致离心泵的指向性开始呈现出偶极性,且正对蜗壳隔舌区域噪声最为剧烈。
由图12(c)可知,在15BPF 时,离心泵辐射噪声的指向性分布初显一定的四极子分布,30°、120°、210°、300°区域声压级明显大于90°、160°、250°、330°区域。 在30BPF 时,其指向性的四极子分布更加明显,70°、120°、230°、310°区域声压级明显大于40°、90°、210°、270°区域,且150°和330°方向的声压级强于70°和230°方向的声压级。 这说明在15BPF至30BPF 的频段内,离心泵的指向性分布主要受离心泵运行时,其内部的动量通量脉动(雷诺应力)诱导的四极子声源影响。 其中,正对隔舌区域的噪声最为强烈,这是因为当叶片尾缘掠过隔舌时,产生了空化现象,四极子声源在空泡溃灭带来的高速微射流与蜗壳壁面的干涉过程中发生了散射,从离心泵内部通过蜗壳壁面传递到外声场中。
4 结论
基于声学无限元方法计算了离心泵的辐射噪声,分析了其声功率谱、声压分布云图以及指向性分布图,主要结论如下:
(1) 利用Lighthill 声类比理论提取离心泵运行时基于体积和基于表面的空气动力源,通过声学有限元、无限元相结合的声振耦合方法求解离心泵辐射噪声可行。
(2) 离心泵运行时产生的辐射噪声主要分布在低频率范围,其辐射声压级在轴频48 Hz 时达到最大值为108 dB,随后声压级强度随着频率的增大而降低。
(3) 离心泵辐射噪声声压级分布在不同的频段具有不同的指向性,在APF~5BPF 频段内,离心泵的指向性分布较为均匀;在5~10BPF 频段内,离心泵的指向性分布呈现偶极子分布,主要受叶片和蜗壳隔舌振荡影响,且正对蜗壳隔舌区域的噪声最为剧烈;在15~30BPF 频段内,离心泵的指向性分布呈现四极子分布,主要受到隔舌区域空泡溃灭带来的高速微射流与蜗壳壁面干涉作用影响。

