基于正弦余弦的自适应教与学优化算法

李会荣，任春年，魏倩茹

（商洛学院 数学与计算机应用学院，陕西商洛 726000）

教与学优化算法（Teaching-Learning-Based Optimization，TLBO）是由 Rao 等[1]模拟班级教学过程提出一种新型群体智能优化算法。教与学优化算法与其它群智能优化算法类似，都是基于种群的元启发式随机优化算法，具有算法原理简单、参数少、寻优性能好、易于实现等优点，目前已经在函数优化、多目标优化、工程参数优化等领域得到了广泛的应用[2-4]。然而，TLBO算法在求解高维复杂优化问题时会出现早熟收敛、收敛速度较慢等问题，通常不能收敛到全局最优[5]。为此，许多研究者对TLBO算法进行了改进，例如，Rao等[5]将变异算子和精英策略融入到TLBO算法中，提出了一种精英教与学优化（ETLBO）算法。于坤杰等[6]提出了一种基于反馈的精英教与学优化（FETLBO）算法，该算法在ETLBO算法中融入反馈机制，可以增加教师与学困生之间的反馈交流，有效增强了算法的局部搜索能力。李会荣等[7]提出了一种自适应教学因子，将差分变异策略融入到TLBO算法中，提出了一种融合差分变异的教-学优化算法，增强了算法的寻优性能。李丽荣等[8]在教学阶段引入非线性动态学习因子和动态随机搜索策略，提出了一种具有动态自适应学习机制的教与学优化算法。欧阳城添等[9]利用Tent映射反向学习策略初始化种群。在教学阶段，对教师个体执行天牛须搜索算法；在学习阶段，对学生个体进行混合变异，提出了一种新的融合改进天牛须搜索的教与学优化算法。王培崇等[10]利用Chebyshev混沌映射初始化种群，利用动态学习因子维持种群的多样性，对教师个体将执行共轭梯度搜索，对种群内适应度较差的学生个体利用反向学习和高斯学习进行了二次学习优化，提出了一种改进的混合混沌共轭梯度法教与学优化算法。黎延海等[11]引入随机交叉策略和“自学”策略来提高算法的全局寻优能力，提出了一种基于随机交叉-自学策略的教与学优化算法。上述这些改进算法虽然能够较好地提高TLBO算法的性能，但往往需要引入额外算子或者算法后期会出现早熟收敛现象。为了改善TLBO算法求解高维复杂问题的能力，本文结合正弦余弦算法，提出一种基于正弦余弦的自适应改进的教与学优化（ASCTLBO）算法。该算法在教学阶段引入自适应教学因子和非线性惯性权重，增强算法局部搜索能力。在学习阶段通过正弦余弦算法维持种群的多样性，提高算法的全局搜索能力。

1 基本教与学优化算法（TLBO）

基本TLBO算法通过利用教师知识水平与班级学生学习的平均水平之间的差异来促进学生之间相互学习，以此来提高班级的整体学习水平[12]。在基本TLBO算法中，班级学生总人数为种群规模，学生的学习成绩即为适应度值，教师表示整个种群学习成绩最好者。TLBO算法分为教学与学习两个阶段，教学阶段是学生向教师学习，学习阶段是学生之间互相学习。假设种群规模为N，空间维数为n，每个学生表示为Xi={Xi1，Xi2，…，Xin}，用适应度函数 f(Xi)表示第 i个学生的学习水平。

1.1 教学阶段

在教学阶段，教师通过向学生传授知识提高班级的整体学习水平，希望班级的平均学习水平Xm向自身Xi靠近。因此教学阶段的迭代方程为：

其中，Xi和Xi,new分别表示第i个学生学习前和学习后的知识水平，表示班级全体学生的平均知识水平，Xt表示教师的知识水平，rand是区间[0,1]的随机数；TF是教学因子，反映教师对班级整体学习水平的影响，一般取值为1或2，即表示为：

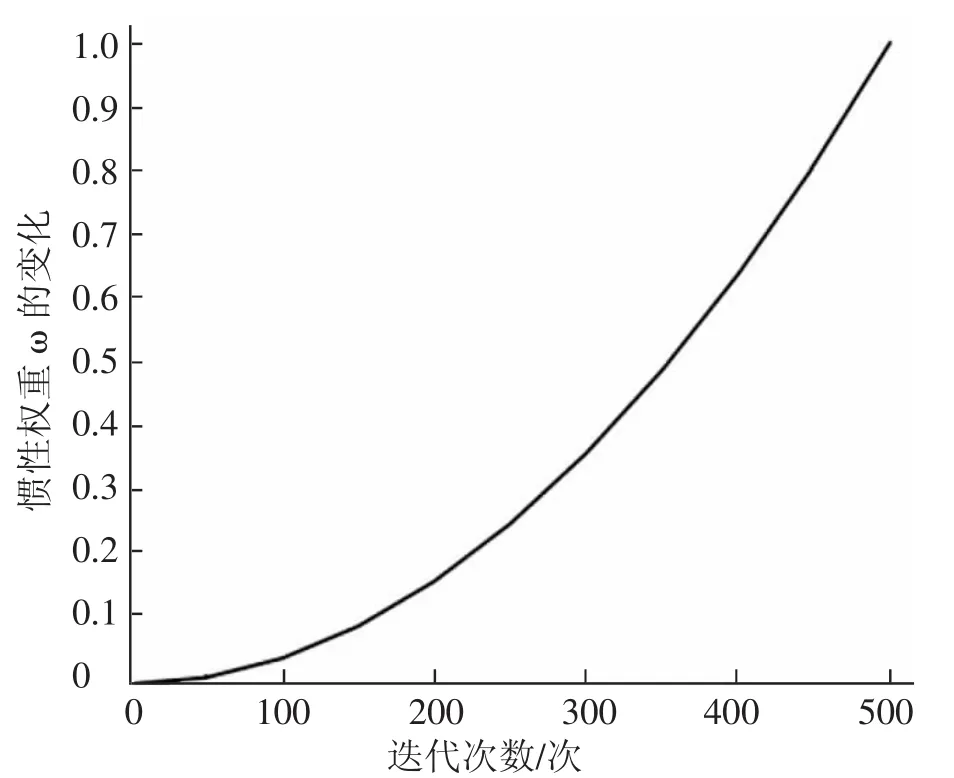
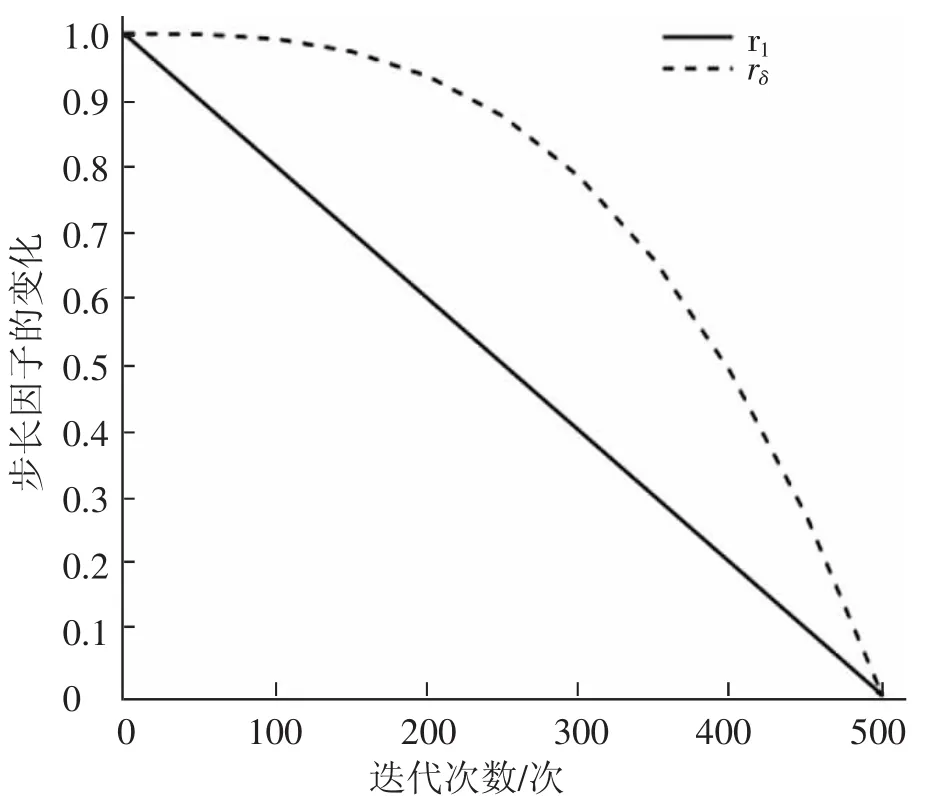
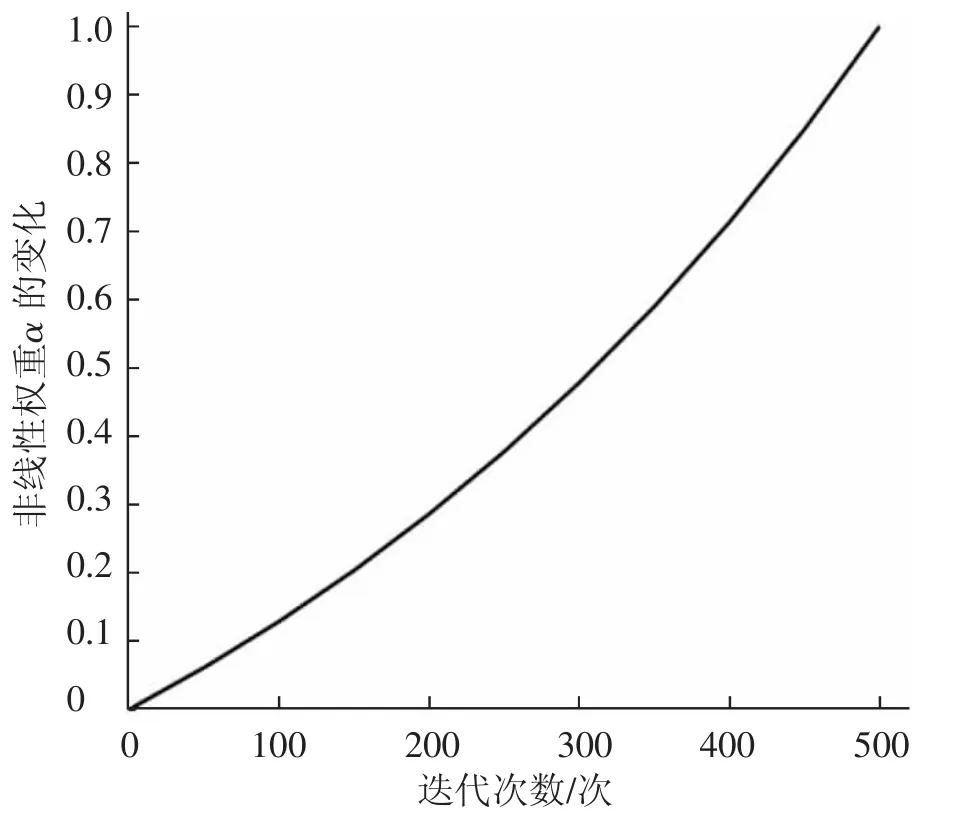
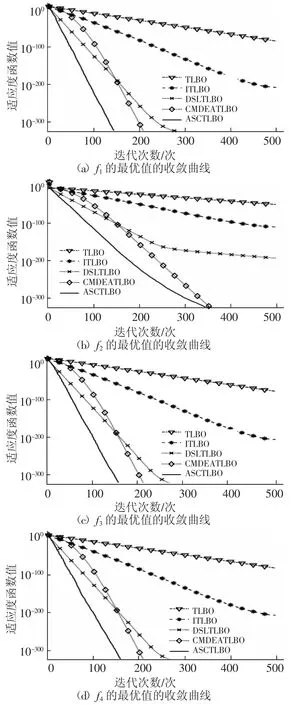
利用学生个体学习水平（即目标函数值）来衡量学习者个体的优劣，如果适应度函数f(Xi，new)

1.2 学习阶段

学习阶段主要依靠学生个体之间相互学习而提高班级整体学习水平。学生Xi随机向学生Xj进行差异性学习，迭代方程为：

如果适应度函数 f(Xi，new)

2 基于正弦余弦的自适应教学优化算法（ASCTLBO）

2.1 自适应教学因子

在基本TLBO算法中，教学因子影响着班级平均学习水平的变化。由式(2)可知，取值为1或2，表示在学习过程中学生没有学到任何知识，或者学到了教师所传授的全部知识。但是在实际教学过程中，由于教学任务、教学重难点及学生接受知识能力不同等因素影响，导致面对简单知识点学生接受能力较强，面对重难点时学生接受能力较弱。在TLBO算法中，TF越小表示搜索步长越小，搜索能力较弱，收敛速度较慢。而TF越大表示搜索步长较大，搜索能力较强，收敛速度较快。为此，将教学因子TF随迭代次数自适应调整为：

其中，TFmin表示最小教学因子，t表示当前迭代的次数，T表示最大的迭代次数。

从式(4)可以看出，随着算法的迭代次数增加，TF从1+TFmin线性递减到TFmin。当算法开始迭代时，教学因子TF为1+TFmin，表示学生学习知识的能力较强，同时算法的全局搜索能力增强。随着迭代次数的增加，教学因子逐渐趋于TFmin，表示在学习过程中，学习难度增强，学生接受知识的能力降低，同时算法的局部搜索能力增强（本文中取TFmin=1）。

2.2 自适应惯性权重

在教学阶段，教师通过“教”阶段提高班级的整体学习水平。从式(1)可以看出，学生要么学习到教师传授的所有知识，要么没有学习到任何知识，与班级学生学习实际情况并不符合，忽视了不同学生的学习差异。为此，引入自适应惯性权重，将迭代方程式(1)更新为：

其中，ω∈[0，1]为惯性权重，本文取 θ＝2，如图1所示。由式(5)可得，在算法早期，学生主要是向教师学习，随着迭代次数的增加，ω逐渐增大，学生维持自身学习的能力逐渐增强，对教师的依赖性逐渐减弱。这种机制和生活中的实际教学情况一致，早期学生主要是向教师学习，学习效率高。随着班级平均水平不断增长，教学难度变化，学生学习效率开始下降，因此，学生会选择性地学习教师讲授的知识，从而增强了算法的局部搜索能力。

图1 迭代次数对惯性权重ω的影响

2.3 正弦余弦算法

在学习阶段，学生选择的教师非常重要，影响整个班级的学习水平。考虑到班级内学生个体选择的最优教师可能不同，学生最终学习情况也会不相同。如果学生找到局部最优教师时，大量学生个体会向寻找到的局部最优教师学习，从而使得整个种群停滞不前，种群的多样性减弱，容易出现早熟收敛现象。针对此现象，本文在“学”阶段引入正弦余弦算法[13]，通过利用正弦余弦算法的震荡变化性质，保持种群的多样性，使得算法的全局搜索能力提高。

其中，λ 为调节系数，本文取 λ＝3，rδ在迭代前期递减速度慢，所以rδ在前期权重较大，有利于提高算法在全局的搜索能力，迭代次数大于1/3时，曲线转折幅度较大，之后进入局部寻优，随着迭代次数增加，rδ逐渐减为0，有利于算法前期在全局搜索能力增强，后期局部搜索能力增强[14]。图2为步长因子r1、rδ随迭代次数变化曲线图。

图2 迭代次数对步长因子r1、rδ的影响

由于TLBO算法在整个寻优过程中，个体更新会受到自身的影响，引入非线性权重α，使得个体在更新过程中自身的影响呈非线性变化，如图3所示，在算法初期，α值较小，个体更新时受到自身的影响较小，全局搜索能力增强。在算法后期，α值较大，个体受到自身影响较大，增强局部搜索能加强算法的收敛速度。因此将学习阶段式(3)表示为：

图3 迭代次数对非线性权重α的影响

其中，r2∈[0，2π]决定学生个体学习的位置，r3∈[0，2]决定教师对学生个体的影响，r4∈[0，1]的随机数，控制算法使用正弦函数还是余弦函数。

综上，提出ASCTLBO算法的实现步骤为：

步骤1 设置种群规模N，空间维数n，最大迭代次数T，当前迭代次数t=1。

步骤 2 初始化种群 X={X1，X2，…，Xm}，计算适应度函数f(Xi)。

步骤3 教学阶段按式(4)～式(6)更新个体，保留最优个体。

步骤4学习阶段根据正弦余弦算法，按式(4)、式(8)、式(9)更新个体。

步骤5 令t=t+1，返回到步骤3，直到满足停止条件或达到最大迭代次数，迭代停止，输出最优解。

3 结果与分析

3.1 测试函数

为验证提出ASCTLBO算法的性能，选取9个标准测试函数进行数值试验[15]，测试函数的表达式如表1所示（n表示空间的维数），并与TLBO[1]、ITLBO[16]、DSLTLBO[8]、CMDEATLBO[17]进行比较。在表1中，函数的最优值均为0，其中f1～f5为单峰函数，f6～f9为多峰函数。

表1 测试函数

参数设置为：种群规模N=30，最大迭代次数T=500，教学因子最小值TFmin=1。其它参数：λ=3，θ=2。得到的最优值（Opt）和最优值的方差（SD）如表2所示，最优值加粗表示。本文采用的测试环境为：Intel(R)Core(TM)i7-9750H 2.60GHz CPU，16GB内存；Windows11操作系统；MATLAB R2020a软件。

表2 单峰测试函数结果对比

3.2 收敛精度分析

数据维数分别为30维、50维、100维下进行试验，每次试验独立运行30次，试验结果如表2和表3所示，其中Opt、SD分别表示每组试验运行30次的最优值与方差。

表3 多峰测试函数结果对比

从表2可以看出，提出ASCTLBO算法、CMDEATLBO算法在单峰函数f1～f4中均达到最优值，方差均为0，但是在单峰函数f5中，提出ASCTLBO算法的性能明显优于其余四种相比较的算法，从而表明提出ASCTLBO算法在单峰函数上具有明显优势。由表3可知，提出ASCTLBO算法在多峰函数f6、f7和f9均取到理论最优值0，而在 f8上，ITLBO、DSLTLBO、CMDEATLB 和提出ASCTLBO算法取得最优值为8.88×10-16，但是在测试函数f8、f9中，提出ASCTLBO算法的方差明显优于其他算法。从表2和表3可以看出，无论在单峰函数还是多峰函数，无论是低维还是高维，提出ASCTLBO算法在最优值、标准差方面的性能都优于其他算法。

3.3 收敛曲线分析

为了分析提出ASCTLBO算法的收敛速度，图4和图5给出在50维数下f1～f9的最优值随着迭代次数的收敛曲线图，其中横坐标为迭代次数，纵坐标为取常用对数。

图4 50维数下f1～f4的最优值的收敛曲线

图5 50维数下f5～f9的最优值的收敛曲线

由图4和图5可以看出，提出的ASCTLBO算法在收敛速度与精度上均优于其他四个算法，说明了自适应惯性权重和正弦余弦算法在前期有着较强的全局搜索能力，加快了收敛速度。其中ASCTLBO算法在 f1、f2、f3、f4收敛曲线下降速度最快，只有 f2收敛曲线在后期稍微变慢，在迭代350次时与DSLTLOB算法交叉，说明ASCTLBO算法引入正弦余弦算法增强了全局搜索能力。f6、f7收敛曲线可以看出，ASCTLBO算法收敛性能优于TLBO、ITLBO、DSLTLBO和CMDEATLBO算法，在运行20次内就找到全局最优值。只有f5和f8收敛曲线在迭代后期出现平缓现象，陷入局部最优，但是收敛速度和精度还是优于相比较的算法。f9收敛曲线图在迭代前200次内多次出现平缓趋势，最后趋于下降。进一步验证了引入的自适应惯性权重有着较强的局部搜索能力，避免算法陷入局部最优解。

3.4 算法复杂度分析

算法的复杂度决定了算法运行所消耗的时间，时间越长，算法越复杂，运行效率就会降低。如表4所示，9个测试函数在相同维数下，ASCTLBO算法运行耗时均少于其他四种算法，且耗时低于TLBO算法。随着维数的增加，整体运行时间变长，但ASCTLBO算法耗时依旧是五种算法中最少的。说明引进的自适应惯性权重和正弦余弦算法并没有增加算法的复杂度，进一步显示出提出的ASCTLBO算法的优越性。

表4 算法运行时间

3.5 工程优化问题应用

为验证提出ACSTLBO算法在工程设计优化中的性能，选取约束工程优化—压缩弹簧设计问题[18]进行数值试验。首先利用罚函数法将其转化为无约束优化问题，再利用提出ACSTLBO算法进行求解。参数设置为：迭代次数 T＝500,λ＝3，θ＝2。压缩弹簧设计是在一定的约束条件下寻找最小化的弹簧重量，其中约束条件主要有最小偏差（g1）、剪切应力（g2）、震荡频率（g3）、外径限制（g4）、弹簧金属丝平均直径 d（x1）、弹簧圈平均直径 D（x2）和弹簧有效圈数 N（x3），则数学模型：

目标函数：

约束条件：

边界约束：

在压缩弹簧设计问题上试验结果如表5所示。由表5可以看出，与TLBO、ITLBO、DSLTLBO及CMDEATLBO算法相比，提出的ASCTLBO算法性能最优，最小值为0.012 685，从而表明ASCTLBO算法在复杂工程优化问题的求解中是有效的。

表5 压缩弹簧设计问题比较

4 结论

针对基本TLBO算法的不足，提出一种基于正弦余弦的自适应教与学优化（ASCTLBO）算法。在教学阶段，引入非线性教学因子和自适应惯性权重，使得当前个体向全局最优个体学习，保证种群的多样性。在学习阶段，利用正弦余弦算法的震荡变化特性，有效保持了种群的多样性。数值试验表明，提出的ASCTLBO算法在全局搜索能力、收敛速度和收敛精度上都优于其比较的算法，同时提出ASCTLBO算法在解决压缩弹簧设计实际问题上具有明显的优越性。