一个幂函数不等式的推广

刘丹华

一个幂函数不等式的推广

刘丹华

（郑州商学院 通识教育中心，河南 郑州 451200）

不等式；Lagrange乘数法；多元函数

1 引言及预备知识

各种事物间存在着大量的不等关系，不等式在理论研究和生活实际中有着非常广泛的应用[1-6]．文献[7]给出了不等式

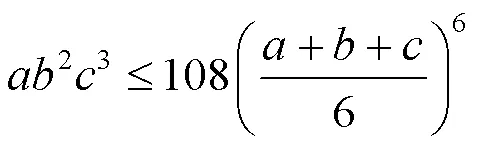
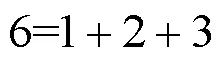
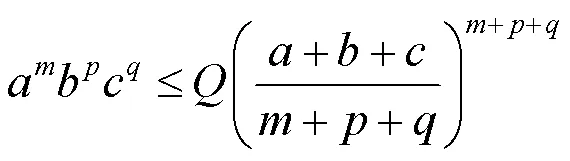
2 主要结果及证明

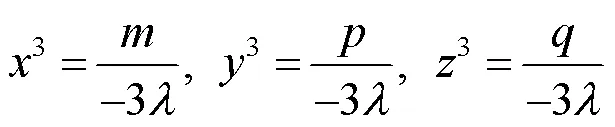
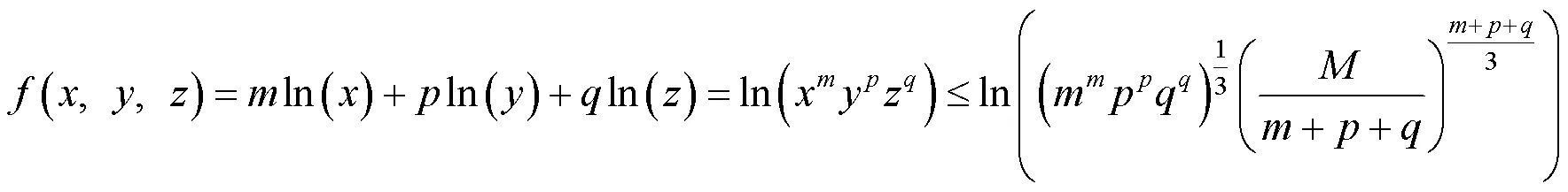
由对数函数的单调性及式（5）可知

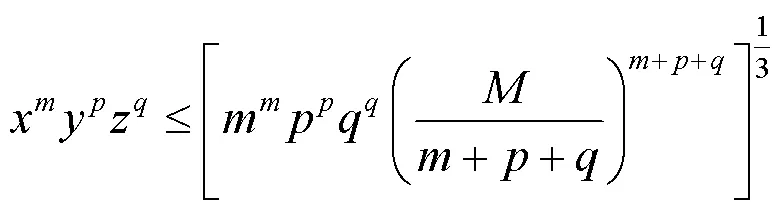
式（6）两边同时取三次方，得

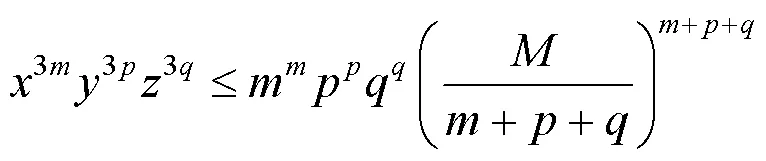
由于

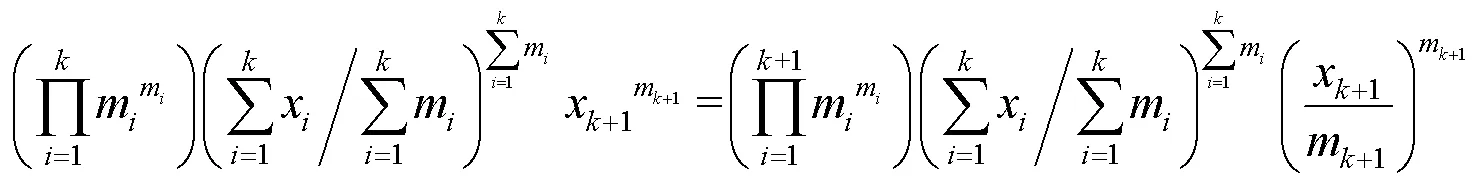
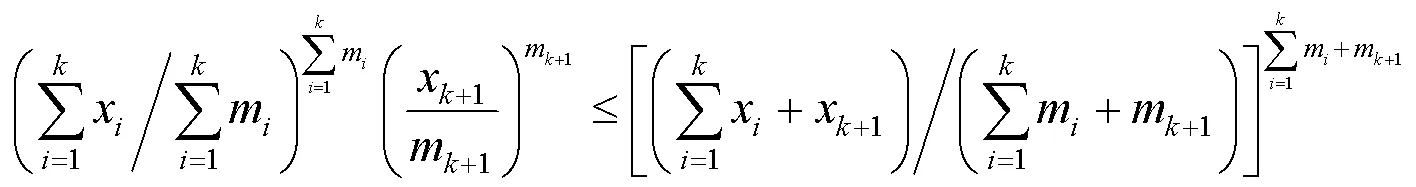
证毕．

注由拉格朗日乘数法适用于有限维函数及定理1的证明可知，定理2还可用拉格朗日乘数法证明．

3　结语

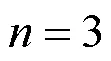
[1] 匡继昌．常用不等式[M]．4版．济南：山东科学技术出版社，2010．

[2] 尚亚东，游淑军．凸函数及其在不等式证明中的应用[J]．广州大学学报（自然科学版），2005（1）：1-6．

[3] 贾延．高等数学教学中定积分不等式的证明方法[J]．宁波教育学院学报，2018，20（2）：76-78，116．

[4] 姚志健．泰勒公式在证明不等式中的应用[J]．兰州文理学院学报（自然科学版），2015，29（1）：86-89．

[5] 景慧丽，杨宝珍，刘华，等．一个不等式的证明方法探讨[J]．重庆工商大学学报（自然科学版），2014，31（8）：24-26．

[6] 徐利治．评匡继昌著《常用不等式》第三版[J]．数学研究与评论，2004（3）：569-570．

[7] 陈纪修，於崇华，金路．数学分析（下）[M]．北京：高等教育出版社，2004．

[8] 张祖峰，胡珍．一个不等式的三种证法[J]．宿州教育学院学报，2014，17（6）：223-225．

[9] 同济大学数学系．高等数学（下）[M]．北京：人民邮电出版社，2016．

Extension of an inequalitywith power function

LIU Danhua

（General Education Center，Zhengzhou Business University，Zhengzhou 451200，China）

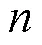
inequality；Lagrange multiplier method；many variables function

1007-9831（2023）07-0014-04

O178

A

10.3969/j.issn.1007-9831.2023.07.004

2022-10-17

刘丹华（1992-），女，河南郏县人，助教，硕士，从事随机过程研究．E-mail：2492868117@qq.com