四维Minkowski空间中伪零曲线的伴随曲线

张佳欣，胡娜，姜杨

四维Minkowski空间中伪零曲线的伴随曲线

张佳欣1，胡娜1，姜杨2

（1. 沈阳工业大学 理学院，辽宁 沈阳 110870；2. 沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110034）

定义了四维Minkowski空间中伪零曲线的伴随曲线．利用伪零曲线的特殊性，将欧氏空间中曲线的性质扩展到伪欧氏空间．通过对伪零曲线及其伴随曲线的Frenet标架的讨论，给出不同类型伴随曲线的曲率函数表达方式．讨论了特殊曲线的伴随曲线的曲率函数，并给出相应实例．

Minkowski空间；伪零曲线；伴随曲线；Frenet标架；积分曲线；曲率函数

1 引言及预备知识

文献[1]在三维和四维欧氏空间中定义了Frenet曲线的一类伴随曲线，并给出这类伴随曲线的一些特征以及与初始曲线曲率之间的关系．本文研究了四维Minkowski空间中伪零曲线的伴随曲线，根据不同类型曲线的特征以及不同Frenet标架之间的关系，得到伴随曲线的一些性质，并给出实例．

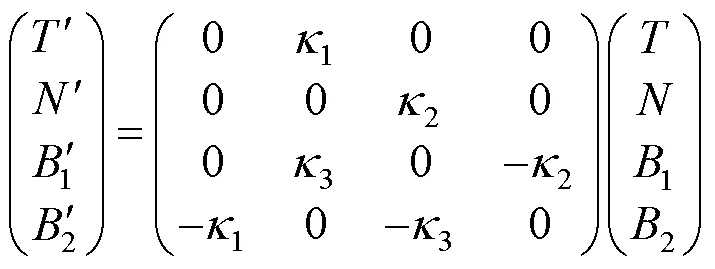
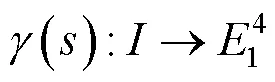
2 主要结果及证明

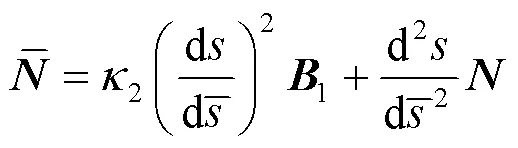
对式（2）做内积，可得

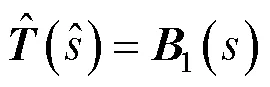
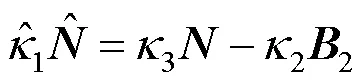
3 结语

随着时代的发展，微分几何学科也逐渐被重视，各类型曲线的伴随曲线也被各界人士所研究，特别是伪零曲线，本文定义并讨论了四维Minkowski空间中伪零曲线的伴随曲线，定义了积分曲线作为伪零曲线的伴随曲线，根据不同类型曲线的Frenet标架的计算，得到伴随曲线的曲率函数．与文献[1-13]中对于这种类型的曲线研究相比大有不同，并且呈现的结果更为清晰，为今后微分几何中这种类型曲线的研究提供了有益的计算经验．

[2] Walrave J．Curves and surfaces in Minkowski space[M]．Sydney：Faculty of Economics & Business Miscellaneous，1995．

[4] Choi J H，Kim Y H．Associated curves of a Frenet curve and their applications[J]．Applied Mathematics & Computation，2012，218（18）：9116-9124．

[5] 杨春辉．曲线的活动标架与达布向量[D]．沈阳：东北大学，2009．

[6] 钱金花，田雪倩．三维Minkowski空间中伪零曲线的表达形式[J]．东北大学学报（自然科学版），2020，41（7）：1061-1064．

[8] Chen B Y．When Does the Position Vector of a Space Curve Always Lie in Its Rectifying Plane?[J]．The American Mathematical Monthly，2003，110（2）：147-152．

[9] Honda S，Takahashi M．Bertrand and Mannheim curves of framed curves in the 3-dimensional Euclidean space[J]．Turkish Journal of Mathematics，2020，44（3）：883-899．

[11] Erdodu M．Parallel frame of non-lightlike curves in Minkowski space-time[J]．International Journal of Geometric Methods in Modern Physics，2015，12（10）：246-248．

[12] Aléssio O．Differential geometry of intersection curves in R4 of three implicit surfaces[J]．Computer Aided Geometric Design，2009，26（4）：455-471．

Associate curve of pseudo null curve in 4-dimensional Minkowski space

ZHANG Jiaxin1，HU Na*，JIANG Yang2

（1. School of Science，Shenyang University of Technology，Shenyang 110870，China； 2. School of Mathematics and Systems Science，Shenyang Normal University，Shenyang 110034，China）

The associate curve of the pseudo null curve in 4-dimensional Minkowski space was defined. The properties of curves in Euclidean space are extended to pseudo-Euclidean space by using the particularity of pseudo null curve. By discussing the Frenet frame of the pseudo null curve and its associate curves，the expression of curvature functions of different types of associate curves were given．The curvature function of the associate curve of a special curve is discussed，and some examples were given.

Minkowski space；pseudo null curve；associate curve；Frenet frame；integral curve；curvature function

1007-9831（2023）07-0018-04

O186

A

10.3969/j.issn.1007-9831.2023.07.005

2022-11-04

张佳欣（1998-），女，辽宁朝阳人，在读硕士研究生，从事微分几何研究．E-mail：zhangjiaxin9919@163.com.

胡娜（1985-），女，辽宁沈阳人，讲师，博士，从事微分几何研究．E-mail：huna19850208@hotmail.com.