一类高阶有理差分方程的动力学性质

全卫贞，李晓培，黄日娣，王丽，周敬人，刘付滢，江建伟，刘世祺

一类高阶有理差分方程的动力学性质

全卫贞1，2，李晓培1，2，黄日娣1，2，王丽1，2，周敬人1，2，刘付滢1，2，江建伟1，2，刘世祺1，2

（1.湛江幼儿师范专科学校 数学系，广东 湛江 524037；2. 岭南师范学院 基础教育学院，广东 湛江 524037）

差分方程；平衡解；局部渐近稳定；全局渐近稳定；素二周期解

1　引言及预备知识

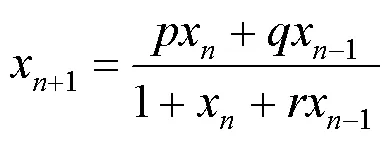
受上述研究的启发，本文研究高阶差分方程

考虑差分方程

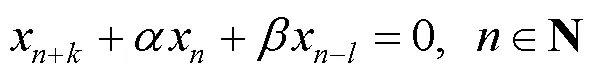
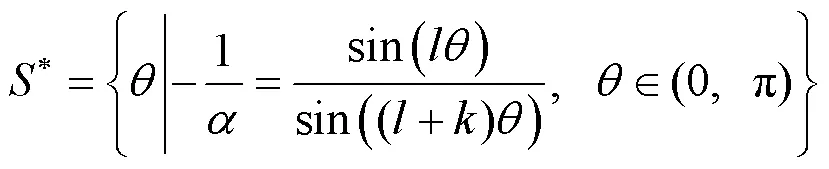
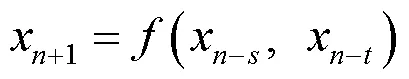
2　主要结果及证明

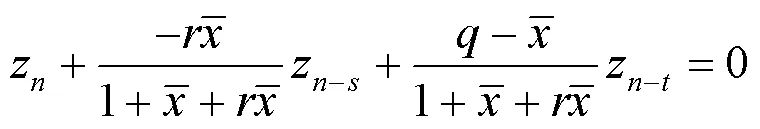
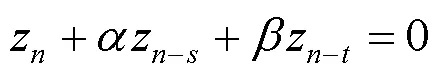
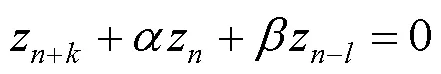
显然，方程（5）与方程（3）等价，方程（3）又与方程（1）等价．所以判断方程（1）解的稳定性态可以转化为判断方程（5）解的稳定性态．

分3种情形来证明：

定理4差分方程（1）无素二周期解．

3　数值计算

图1 差分方程解的图像

4　结语

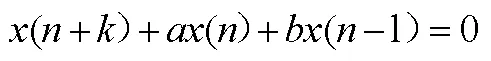
[2] Kulenovic M R S，Ladas G．Dynamics of the second rational difference equations with open problems and conjectures[M]．New York：Chapman Hall/CRC，2002．

[3] 杨懿．几类高阶有理差分方程动力学性质的研究[D]．重庆：重庆大学，2009．

[4] Kelley W G，Peterson A C．Difference Equations with Applications[M]．New York：Acad Press，1991．

[5] Kocicv L，Ladas G．Global behavior of nonlinear difference equations Of higher order with applications[M]．Dordrecht：Kluwer Academic Publishers，1993．

[6] Agarwal R P，Grace S R，Oregan D．Oscillation Theory for Difference Equations and Functioncal Difference Equations[M]．Dordrecht：Kluwer Academic Publishers，2000．

[7] Agarwal R P．Difference Equations and Inequalities[M]．New York：Marcel Dekker，1992．

[9] 李晓艳，谢建民．一类高阶有理差分方程的全局行为[J]．延边大学学报（自然科学版），2016，42（4）：75-81．

[10] 全卫贞．一类三阶有理差分方程的奇点集和解的渐近性[J]．数学的实践与认识，2017，47（1）：42-48．

[11] 李明山，徐江明，周效良．一类差分方程的动力学性质[J]．重庆师范大学学报．2021，38（3）：30-35．

Dynamic properties of a class of higher order rational difference equations

QUAN Weizhen1，2，LI Xiaopei1，2，HUANG Ridi1，2，WANG Li1，2，ZHOU Jingren1，2，LIU Fuying1，2，JIANG Jianwei1，2，LIU Shiqi1，2

（1. Department of Mathematic，Zhanjiang Preschool Education College，Zhanjiang 524037，China； 2. School of Basic Education，Lingnan Normal University，Zhanjiang 524037，China）

difference equation；equilibrium solution；local asymptotic stability；global asymptotic stability；prime two periodic solutions

1007-9831（2023）07-0001-05

O175.7

A

10.3969/j.issn.1007-9831.2023.07.001

2022-10-01

国家自然科学基金项目（11761011）；广东省普通高校特色创新项目（2020KTSCX351）

全卫贞（1980-），女，广西玉林人，副教授，硕士，从事差分方程与动力系统研究．E-mail：quan801015@126.com