基于改进遗传算法优化BP神经网络的表面粗糙度误差预测

张剑飞，王磊，刘明，王硕

基于改进遗传算法优化BP神经网络的表面粗糙度误差预测

张剑飞，王磊，刘明，王硕

（齐齐哈尔大学 计算机与控制工程学院，黑龙江 齐齐哈尔 161006）

随着现代制造业的发展，对工件加工质量和精度越来越追求高标准．表面粗糙度作为评价工件质量的重要指标，对工件质量和产品特性具有重要的影响．针对传统BP（Back Propagation）神经网络在训练过程中易陷入局部极小值和收敛速度慢等不足，遗传算法（Genetic Algorithm，GA）存在随机性问题，提出采用遗传算法和混合蛙跳算法（Shuffled Frog Leaping Algorithm，SFLA）结合来改进BP神经网络（记为SFLA-GA-BP）进行工件表面粗糙度误差预测．以工件表面粗糙度与砂轮粒度、砂轮转速、工件速度、进给率四要素之间的相关关系为研究目标，通过正交实验技术，分别以BP神经网络、遗传算法改进BP神经网络（记为GA-BP）和SFLA-GA-BP神经网络进行建模分析．实验结果表明，SFLA-GA-BP的均方根误差（Root Mean Squared Error，RMSE）比BP网络和GA-BP网络分别提高了1.7%和0.7%、平均绝对百分误差（Mean Absolute Percentage Error，MAPE）分别提高了2%和1.1%，平均绝对误差（Mean Absolute Error，MAE）分别提高了1%和0.6%．SFLA-GA-BP模型的预测误差相比于BP神经网络和GA-BP神经网络更加精准．故SFLA-GA-BP模型对于预测工件表面粗糙度具有更高的准确率和良好的稳定性，同时为企业减少成本，对企业智能化发展具有一定的指导意义．

表面粗糙度；神经网络；遗传算法；混合蛙跳算法

人工神经网络由Rumenlhart[1]等科学家在1986年提出，目前己经被广泛运用在人工智能、医学处理、机械工业等各个领域方面．针对不同的应用需要，学者们做了相关研究．Vogl[2]等提出一种自适应学习率的算法，来减少BP算法的学习时间．研究人员为加快网络模型的训练速度，将其他算法与之结合，取得了良好的效果．马秋芳[3]利用粒子群算法优化BP神经网络来预测城市短时交通流．刘亚丽[4]等利用遗传算法初始化BP神经网络的权值与阈值对BP神经网络进行优化并计算配电网的线损误差．牛华[5]将遗传算法与BP算法结合预测汽车发动机故障．梅妍玭[6]等利用自适应遗传算法与BP神经网络结合去预测船舶交通流量．李超[7]等将粒子群算法和遗传算法结合优化BP神经网络预测船舶电力系统故障．郝娟[8]将粒子群算法与BP算法结合监测SRM转子位置．研究表明，采用BP神经网络建立多输入多输出非线性系统的数学模型具有很强的适应性，如果将其他智能算法与之结合，将更好地发挥BP神经网络的优势．本文将遗传算法（Genetic Algorithm，GA）与混合蛙跳算法（Shuffled Frog Leaping Algorithm，SFLA）结合改进BP神经网络算法，利用遗传算法来保证全局搜索的同时，采用混合蛙跳算法分组策略局部搜索来避免遗传算法的随机性问题，最后通过BP神经网络进行训练以实现对加工工件表面粗糙度的预测，进一步提升算法的误差精度．

1 BP神经网络

BP神经网络[9-10]首先执行输入样本的正向传播过程，从输入层进入，进行权值与阈值的运算，通过激励函数得到的输出作为隐藏层的输入，隐藏层再进行权值与阈值的运算，得到最终输出．其过程是进行加权操作与调用激励函数来获得各层输出值，当误差不满足精度要求时，则执行反向传递，通过梯度下降法不断对权值和阈值进行处理来减小误差．

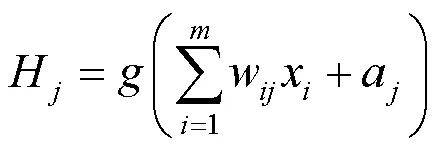
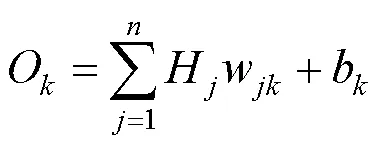
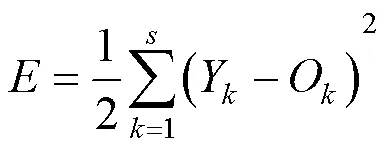
2 混合蛙跳改进遗传BP算法

2.1 遗传算法原理

遗传算法是一种利用模仿生物进化生存规律的自然选择理论[11]，其核心是搜索最优解的数学模型．遗传算法中的个体或染色体是一组基因编码，该基因编码是基于一定的编码方式生成，编码方式较为常用的有实数编码和二进制编码[12]．通过对染色体执行选择、交叉及变异3种操作进化成更优的子群，并根据适应度函数来进行个体评价，在进化过程中逐步向最优个体进化，直到满足期望的收敛要求为止．其目的是为了通过产生新的个体在进化过程中能跳出局部最优．具体描述为：

Step1初始化参数．确定初始化种群的数量、编码的方式、个体编码的长度、选择策略、交叉概率的设定、变异概率的设定、适应度函数的选择、最大迭代次数．

Step2初始种群，选择编码方式进行编码．

Step3选择合适的函数作为适应度值．

Step4进行选择、交叉、变异操作，进化种群．

遗传操作中选择、交叉和变异3种算子具体公式为：

（1）选择操作．计算出所有个体的适应度值，利用轮盘赌算法随机选择个体，个体的适应度值越高，被选中成下一代子群的机率则越大，个体的概率公式为

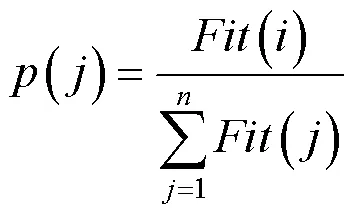
（2）交叉操作．选择个体的某段基因进行交换，交换后产生新的个体

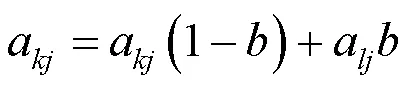
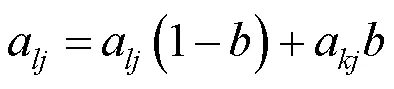
（3）变异操作．通过变异概率产生新的个体

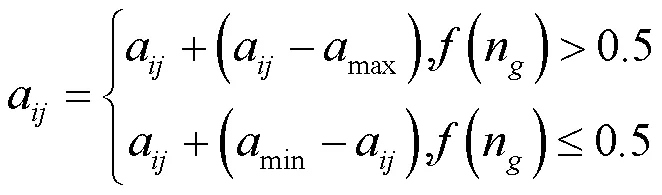
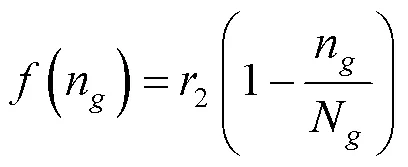
Step5当达到最大迭代次数时，执行Step6，否则，继续执行Step3．

Step6输出结果，解码后得到问题的最优解．

2.2 混合蛙跳算法原理

由于遗传算法的选择操作存在一定的随机性，针对其存在的问题，引入了混合蛙跳的分组策略进行替换轮盘赌算法．混合蛙跳算法于2003年由Eusuff[13]等提出，该算法具有参数少，能够跳出局部最优等优点．

混合蛙跳算法采用全局和局部搜索相结合的并行机制，使算法得到全局最优解．其具体的实现步骤为：

Step1设置相关参数，即青蛙种群数量、各子群中青蛙数量、子群内最大进化次数、种群最大进化次数．计算种群中各个青蛙的适应值．

Step3子群划分．将排序后的种群分别放入每一个子群内，直到所有青蛙种群分配完成．

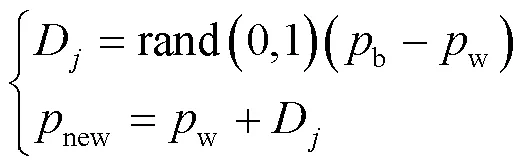
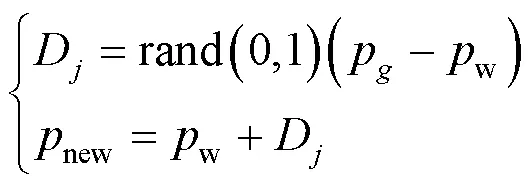
Step5混合子群．将重新混合所有子群，当达到最大迭代次数时，结束循环．否则继续执行Step3．

2.3 SFLA-GA-BP算法的实现

根据研究，提出一种改进的遗传BP神经网络算法．该算法引入混合蛙跳算法的分组策略来替换传统遗传算法选择操作中的轮盘赌算法．其算法流程见图1．

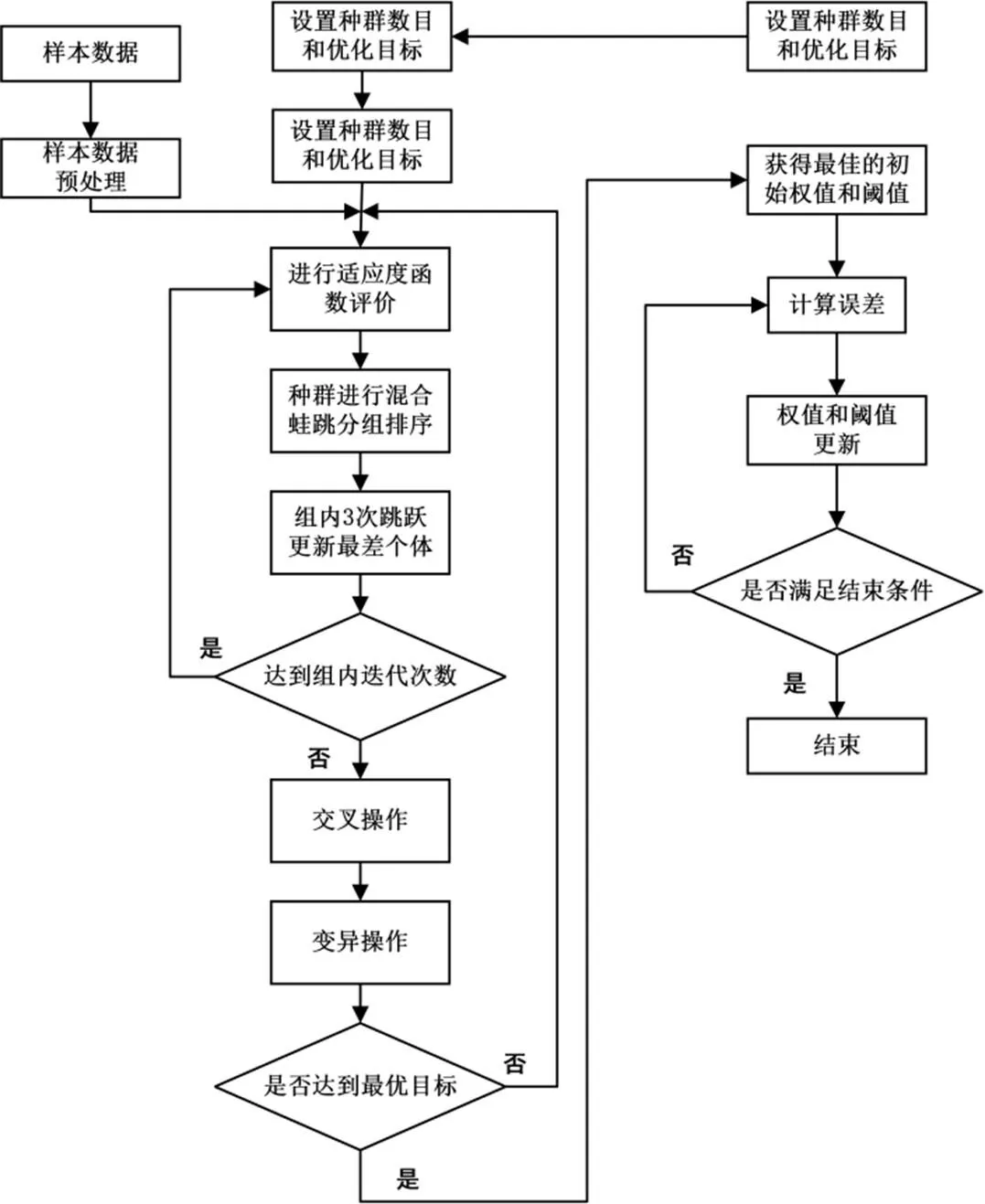
图1 改进遗传算法优化BP神经网络计算流程

实现步骤为：

Step1初始化参数．输入训练样本数据，进行预处理．确定BP神经网络的网络结构．初始化遗传算法的种群数目、编码方式、交叉因子、变异因子、最大迭代次数．初始化混合蛙跳算法分组数目，组内最大迭代次数．

Step2适应度评价．本文采用公式（3）作为适应度函数，记录所有个体的适应度值．

Step3分组更新．按适应度值将所有个体进行从高到低排序，然后进行分组，分组策略为2.2中的Step3子群划分．子群内部进行更新，每个子群中最差个体执行3次跳跃过程，其过程为2.2中的Step4局部搜索．

Step4整体寻优．混合所有子群个体，对混合后的种群进行选择、交叉操作．

Step5输出结果．当达到最大迭代次数时，输出结果，否则跳到Step3重复进行．得到的输出结果即为SFLA-GA-BP算法的初始权值和阈值，然后进行训练．

3 SFLA-GA-BP工件表面粗糙度预测模型建立及结果分析

3.1 数据集介绍

本文所使用数据集来自文献[14]，经重新整理后见表1．实验对象为某轿车发动机四缸缸体，实验选取砂轮颗粒、砂轮转速、工件速度和进给量作为表面粗糙度的主要影响因素．进行传统的神经网络建模时，需有数量充足的样本，有明确的网络模型、网络的权值、阈值以及初始值．从训练BP神经网络的样本s中选择一个体s=[g，r，w，f，sr]，单位分别为#，r/min，mm/min，mm/r，Ra．其中，[g，r，w，f]反映为砂轮颗粒、砂轮转速、工件速度、进给量；[sr]为工件的表面粗糙度．[g，r，w，f]为BP网络样本的输入；[sr]为目标输出．根据正交实验设计准则，经过正确合理的安排后，能够降低试验次数和时间．

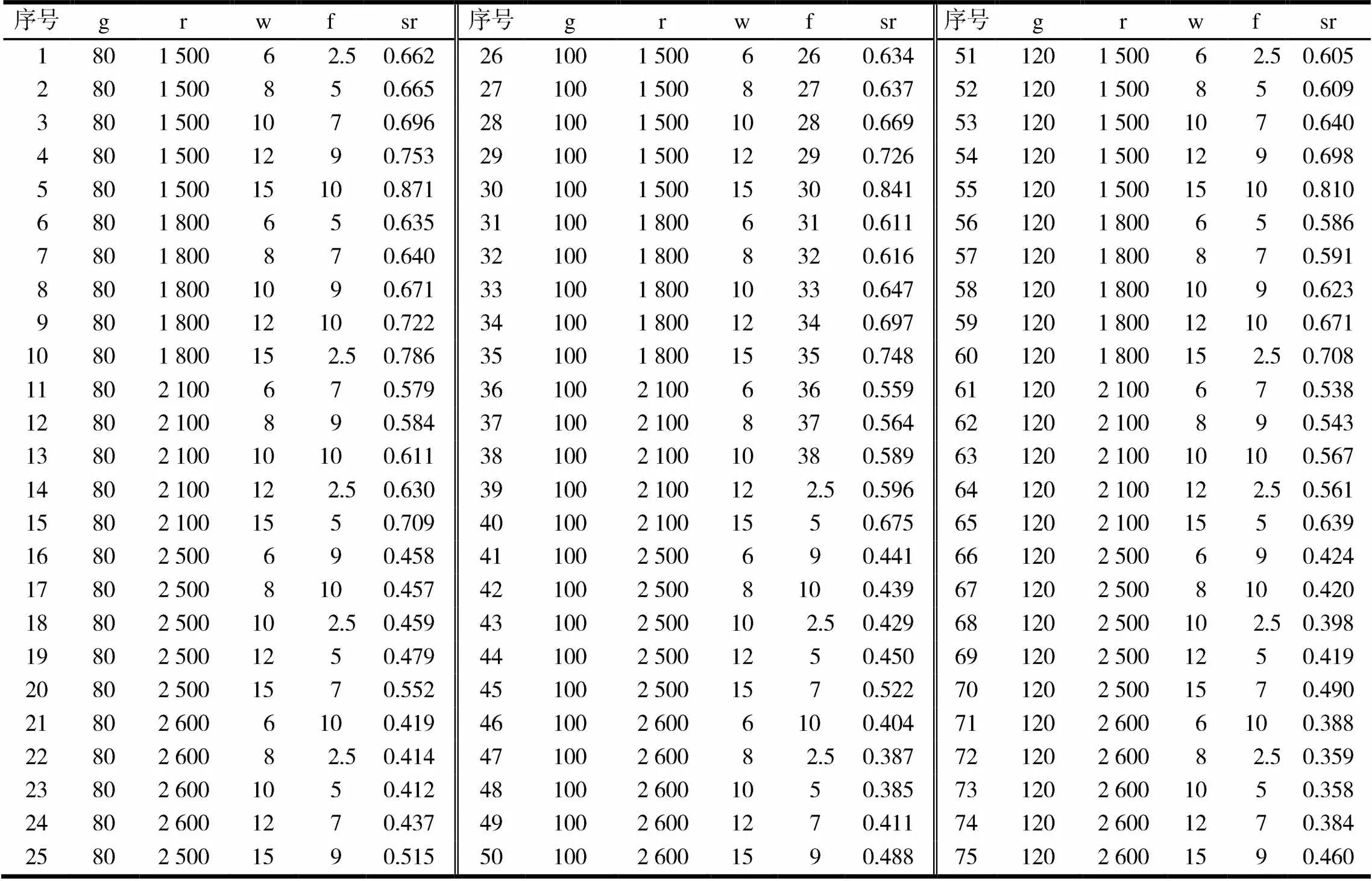
表1 正交实验数据

3.2 评价模型

均方根误差为

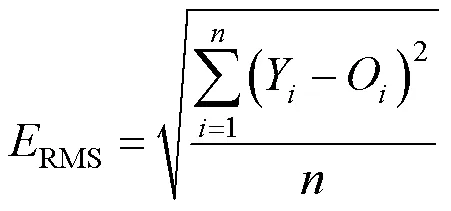
平均绝对误差

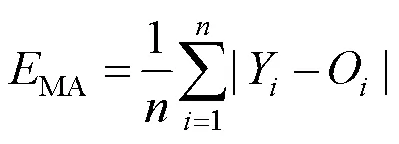
平均绝对百分误差

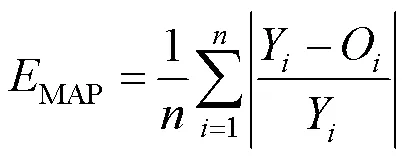
3.3 SFLA-GA-BP神经网络模型建立

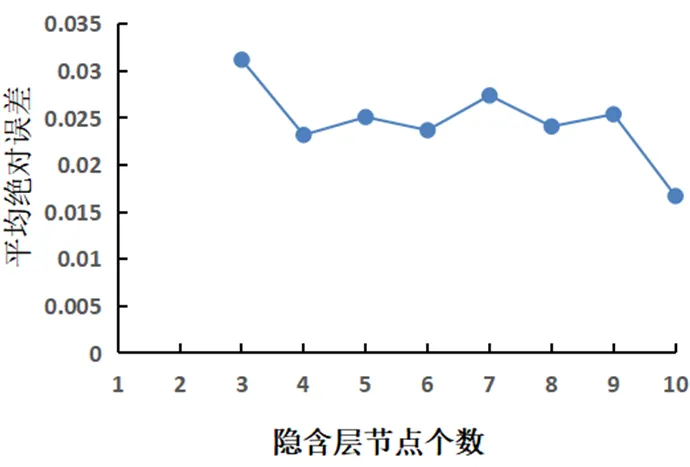
图3 平均绝对误差变化

由于表1中数据数量级差别较大，对神经网络进行训练时，为了减少因数据间较大数值的差别，防止网络收敛速度过慢，需要对数据样本进行归一化操作．其公式为

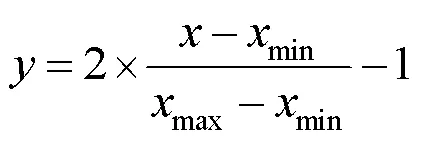
实验方法是基于PC端Win10操作系统进行模型的设计和系统的开发，主要软硬件环境为PyChram-2021，Python3.8，8G Intel-i7-1065G7 CPU．

3.4 结果与分析

其中参数的设置大多数是根据人为经验所设置，其中染色体长度和网络结构是根据输入参数和输出参数的个数所决定的．

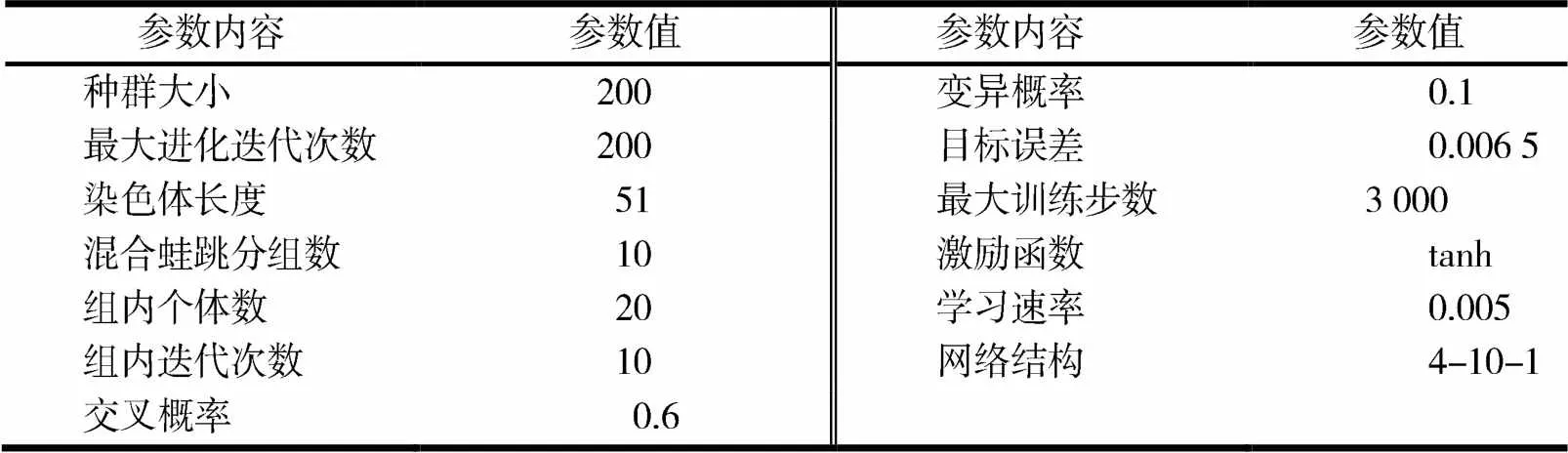
表2 模型参数设置

在网络结构、权值和阈值等条件一致的情况下，各模型的预测误差见表3．BP模型的最大误差为6.65%，最小误差为1.97%，GA-BP模型的最大误差为5.06%，最小误差为0.68%，而SFLA-GA-BP模型的最大误差为3.13%，最小误差为0.15%．

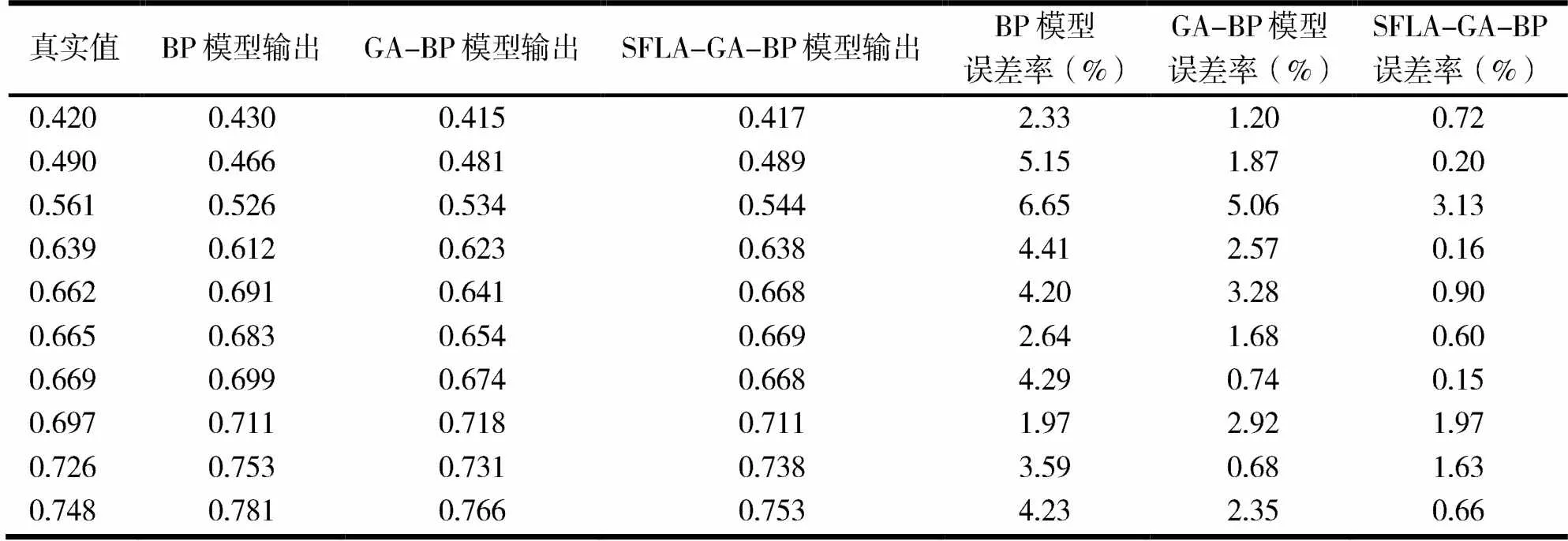
表3 各模型预测结果对比

相对于其他预测工件表面粗糙度的模型，SFLA-GA-BP神经网络具有较好的预测结果（见图4）．相对于传统BP网络和GA-BP网络提高了预测精度．

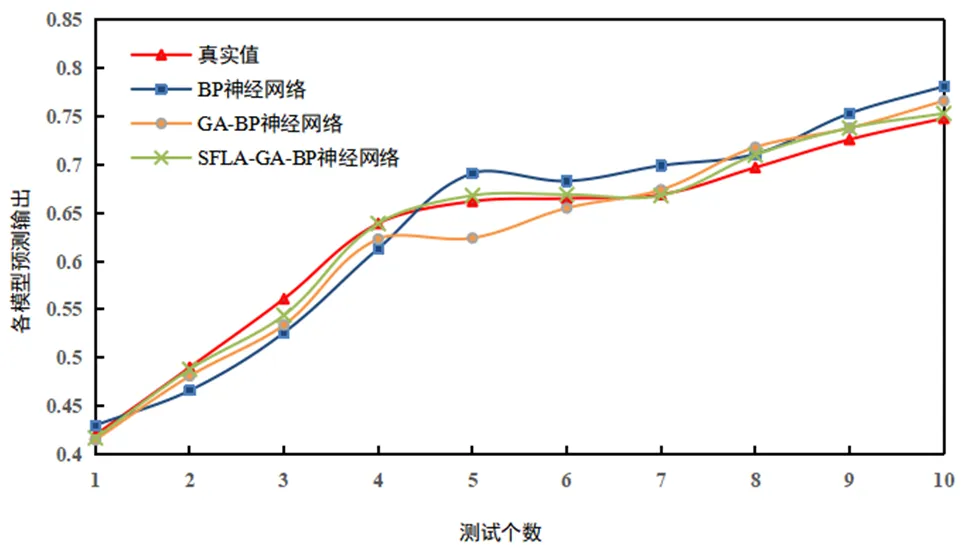
图4 各神经网络预测对比

GA-BP模型在迭代100次以后寻找到最优解（见图5），SFLA-GA-BP在迭代75次左右以后寻找到最优解（见图6），其适应度值的精度也高于GA-BP模型．

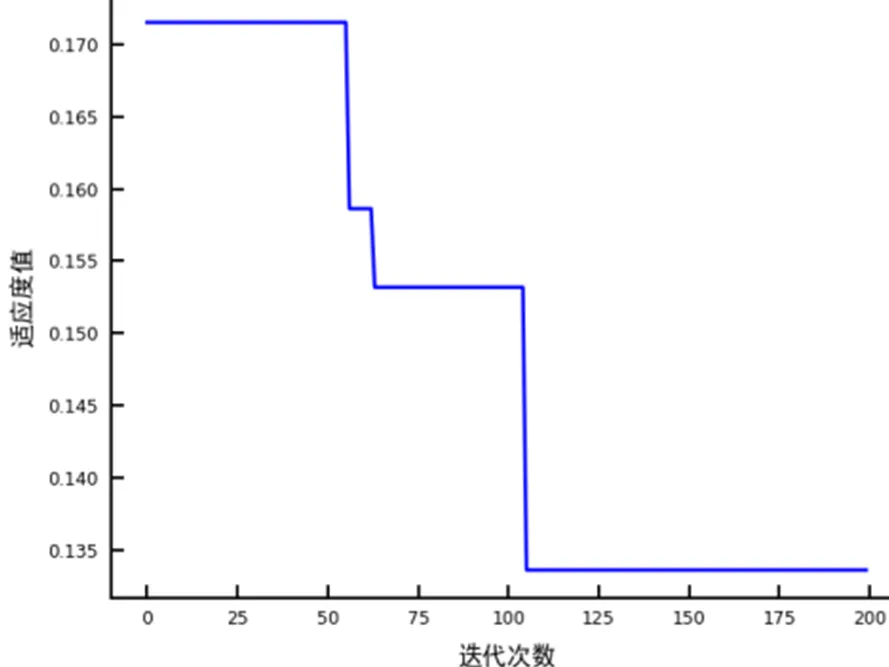
图5 GA-BP网络最优个体适应度值

图6 SFLA-GA-BP网络最优个体适应度值

表4 模型评价指标对比

4 结语

本文以工件表面粗糙度为预测目标，提出的结合遗传算法和混合蛙跳算法优化BP神经网络的设计方法，并与传统的BP模型与遗传算法优化BP模型进行对比．预测结果表明：

（1）使用SFLA-GA-BP算法的预测误差精度高于传统的BP模型与GA-BP模型．

（2）SFLA-GA-BP算法对于预测工件表面粗糙度具有良好的稳定性和有效性．

因此，给出的方法能够在一定程度上为企业减少成本，对企业智能化发展具有一定的指导意义．

[1] Rumelhart D E，Hinton G E，Williams R J．Learning Representations by Back Propagating Errors[J]．Nature，1986，323（6088）：533-536．

[2] Vogl T P，Mangis J K，Rigler A K．Accelerating the convergence of the back-propagation method[J]．Biological Cybernetics，1988，59（4/5）：257-263．

[3] 马秋芳．改进PSO优化的BP神经网络短时交通流预测[J]．计算机仿真，2019，36（4）：94-98．

[4] 刘亚丽，李英娜，李川．基于遗传算法优化BP神经网络的线损计算研究[J]．计算机应用与软件，2019，36（3）：72-75．

[5] 牛华．基于改进BP神经网络的汽车发动机故障诊断[J]．组合机床与自动化加工技术，2021，13（5）：57-61．

[6] 梅妍玭，张得才，傅荣．一种准确预测船舶交通流的自适应遗传算法优化的BP神经网络模型研究[J]．电子器件，2020，43（2）：452-455．

[7] 李超，薛士龙．改进GA-PSO算法的船舶电力系统故障诊断[J]．科学技术与工程，2019（28）：372-377．

[8] 郝娟．基于粒子群算法优化BP神经网络的SRM磁链模型[J]．机械制造与自动化，2018，47（2）：130-132．

[9] 周志华．机器学习[M]．北京：清华大学出版社，2016．

[10] Cybenko G．Approximation by superposition of a sigmoidal function[J]．Mathematics of Control，Signals，Systems，1989，2（4）：303-314．

[11] Miao H，Zuo D W，Wang H J，et al．Optimization of Tap Parameters for Internal Thread Cold Extrusion of High Strength Steel Based on Genetic Algorithm[J]．Key Engineering Materials，2010，898（431/432）：434-437．

[12] 赵红，李滢，肖文洁．实数与二进制编码GA种群多样性统一数学模型[J]．计算机工程与科学，2016，38（6）：1177-1182．

[13] Eusuff M M，Lansey K E．Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm[J]．Journal of Water Resources Planning and Management，2003，129（3）：210-225．

[14] 杨志贤，于萍萍，顾寄南．基于PSO-BP神经网络的磨削表面粗糙度预测模型的研究[J]．工具技术，2017，51（11）：36-40．

Prediction of surface roughness error based on BP neural network optimized by improved genetic algorithm

ZHANG Jianfei，WANG Lei，LIU Ming，WANG Shuo

（School of Computer and Control Engineering，Qiqihar University，Qiqihar 161006，China）

With the development of modern manufacturing industry，the workpiece processing quality and precision are increasingly pursuing high standards．Surface roughness is a significant index to estimatethe surface quality of workpiece，it had significant influence on the quality of machined parts and product performance．Aiming at the shortcomings of traditional BP（Back Propagation） neural networks was effortless to sink into the local minimum and slow convergence rate in the training process，genetic algorithm（GA）had the problem of randomness，according to the genetic algorithm and shuffled frog leaping algorithm（SFLA）were combined to improve BP neural network （named SFLA-GA-BP）to predict surface roughness error．The model taken the correlation between artifacts surface roughness and grinding wheel granularity，grinding wheel speed，artifacts speed and feed rate as the research object，and used orthogonal experiment method．BP neural network，genetic algorithm improved BP neural network （named GA-BP）and SFLA-GA-BP neural network were established model analysis respectively．Experimental show that the root mean squared error（RMSE）of SFLA-GA-BP was 1.7% and 0.7% higher than that of BP and GA-BP，respectively．MAPE increased by 2% and 1.1%，mean absolute error（MAE）increased by1%and 0.6%．The prediction error of SFLA-GA-BP model is more accurate than that of BP neural network and GA-BP neural network．So the SFLA-GA-BP model for predicting the workpiece surface roughness had a higher accuracy and good stability．Meanwhile，it can reduce the cost for enterprises，and has certain guiding significance for the development of enterprise intelligence．

surface roughness；neural network；genetic algorithm；shuffled frog leaping algorithm

1007-9831（2023）07-0033-08

TP39

A

10.3969/j.issn.1007-9831.2023.07.008

2023-03-08

齐齐哈尔市科技计划重点项目（ZDGG-202203）

张剑飞（1974-），男，黑龙江齐齐哈尔人，教授，博士，从事深度学习和计算机辅助诊断研究．E-mail：jian_fei_zhang@163.com