积极心理品质下初中数学人文课堂建构的案例研究
姜丽梅

[摘 要] “勾股定理”是初中阶段具有数学文化背景的典型课题,开展“勾股定理”同课异构教学,对两节课例进行比较,研究积极心理品质下数学人文课堂的建构.教学中导入数学文化是渗透数学思想方法和文化价值的有效举措,不仅点燃了学生的学习热情,使学生拥有价值感悟,而且中国数学史还加强了学生的爱国之情,有助于培养学生的积极心理品质.
[关键词] 积极心理品质;人文课堂;同课异构;数学文化
基于积极心理品质培养的初中数学人文课堂建构旨在数学课中挖掘教材所隐藏的各种思想方法,增强数学与生活的联系,有意识地运用数学思维方式处理问题,增强学生的推理能力,让学生感觉思考的价值与魅力,激发学生智慧生成,实现价值引领和自我修养的和谐统一.
近日,闵晓颖名师工作室组织了以“培养学生积极心理品质下的初中数学人文课堂教学”为专题的“勾股定理”同课异构的教学研讨活动. “勾股定理”是一个典型的具有数学文化背景的课题,各位教师在教材背景的理解下设计的教学过程是不尽相同的. 笔者以此活动为契机,探讨同一课题、不同时机导入数学文化的问题解决方式和最有效的路径.
课例背景素材
“勾股定理”是人教版《义务教育教科书·数学》八年级下册的内容,在这之前,学生已经学习了“相交线与平行线”“三角形”“全等三角形”“等腰三角形”,经历了观察、实验、探究、归纳、推理、证明等全过程,了解了一些简单几何体和平面图形及其基本特征,会进行简单的逻辑推理和三种语言的转换.
在中国,相传4000多年前大禹曾在治理洪水的过程中利用勾股定理来测量两地的地势差. 在3000多年前,中国人已经知道用边长为3,4,5的直角三角形进行测量[1].
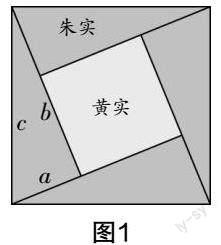
在三国时期,吴国赵爽利用他创制的勾股方圆图详细证明了勾股定理,他在自己的数学文献《勾股方圆图注》(《周髀算经》的注文)中写道:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四. 以勾股之差自相乘为中黄实. 加差实,亦成弦实. ”[2]这是利用面积不变的关系,结合图形面积的不同算法得到等量关系[3]. 如图1所示,人们称它为“赵爽弦图”,被选为2002年在北京召开的国际数学家大会的会徽[4].
课例比较分析
市区两所不同学校的教师A和教师B各自上了一节“勾股定理”课. 两节课的教学流程均包含六个环节,分别为情境引入、动手操作(操作验证)、验证归纳(交流展示)、知识应用、课堂小结、作业. 两节课的教学目标基本相同,包括:①了解勾股定理及其文化历史,感受数学文化的魅力,进一步激起爱国主义情怀;②经历拼图活动,发展动手能力、合情推理能力,体验数学思维的严谨性,初步领会用面积法解决几何问题的思路. 探究和证明勾股定理是两节课的教学重点和难点. 但两节课也有不同之处,一是教学活动的进度安排不同,二是导入数学文化的时机和方法不同. 两节课具体的教学流程如表1所示.
1. 教学活动的进度安排不同
教师A开门见山地揭示了本节课的课题——学习直角三角形的三边关系,然后让学生按要求动手操作,猜想直角三角形的三边关系,再让学生在小组内验证说明,最后引导学生总结研究方法,适当板书,并对勾股定理的数学史加以文字拓展. 本节课一开始就调动学生进行动手操作,在形式上做到了生生互动和师生互动. 但实际上学生是被动的,按照要求进行讨论、合作,他们的活动是按部就班、受到限制的,不利于学生深入思考,实现深度学习.
教师B从生活中提出问题,引发学生思考后呈现一段数学史料,通过对地毯的放大观察,正式开展本节课对勾股定理的探究. 通过观察教师在几何画板上的动图,学生深入思考,猜测直角三角形的三边关系,再动手操作验证. 虽然教师B对动手操作的安排比教师A稍晚一些,但学生是在他们各自有了想法后进行的操作验证,这样的活动是有想法、有灵魂的活动. 而且教师B善于观察,重视学生不一样的验证方法,激发学生深度思考和学习. 教师B与学生的互动和总结都是恰到好处的.
2. 融入数学文化的时机和方法不同
教师A在学生动手操作、猜想和验证后揭示勾股定理,用文字介绍勾股定理的数学文化. 这里教师A采用点缀式教学法融入数学文化,反映了相关的数学史. 教师A的教学目标明确,有指导性地放手让学生探究和证明直角三角形的三边关系,注重学生动手操作、合情推理的能力.
教师B在本节课的导入环节就融入了数学文化,呈现方式多样,有故事叙述的附加式、视频播放的复制式以及将研究图形设置成面积问题的顺应式等. 数学文化氛围特别浓厚,贯穿了本节课的始终.
教师B从预设的数学文化出发,呈现数学家发现等腰直角三角形三边关系的过程,引发学生的好奇心和求知欲,然后让学生用网格纸从特殊的直角三角形的三边关系探究到一般的直角三角形. 在验证猜想前,教师B用几何画板进行动态演示,自由拉动直角三角形的任意一条边,学生从线段长度上直观发现结果仍然是成立的,之后再让学生动手操作去验证. 此时学生的验证方法让课堂焕发出了不一样的光彩,比如一个学生只用两张全等的直角三角形卡纸就能驗证勾股定理,体现了“教学重生成”的观念. 这样不仅让学生尝到了成功的乐趣,而且增强了学生学习数学的自信心.
结论与教学启示
1. 积极心理品质下的人文课堂
两节课均是基于积极心理品质,围绕学生的核心素养培养而设计的,给予学生充分的时间和空间去发现问题、分析问题和解决问题,让学生独立思考、合作交流、大胆展示.
两节课均用割补法验证勾股定理,其中渗透了转化思想,即把不容易求面积的图形通过分割或填补转化为熟练的图形来求面积,这也体现了等积变换思想. 特别地,教师B注重方格纸的使用,降低了学生导入学习的难度,学生容易想到用割补法去计算验证.
两节课皆是通过图形研究,得到直角三角形三边关系的,渗透了数形结合思想方法,而且融入了“赵爽弦图”和国际数学家大会会徽等数学文化,点燃了学生的学习热情,加强了学生的爱国之情和自信心,有助于培养学生的积极心理品质.
2. 同课异构,精彩在“异”
两节课的教学目标均已达成,但值得强调的是教学目标应该以学生的学习目标为标准. 在两节课中,学生均掌握了勾股定理的知识点,但他们在感受数学文化魅力和爱国情怀上却有着巨大差距,究其根本在于两节课融入数学文化的时机和方法不同. 相比之下,教师B的教学设计更胜一筹,最能体现基于积极心理品质培养的人文课堂建构的教学理念.
3. 数学文化的重要性
教师对数学文化的掌握尤为重要,只有教师充分掌握了知识的文化背景,才能传道授惑于学生. 学生对数学文化的掌握也非常重要,只有学生深入了解了数学文化(特别是我国的数学文化背景和数学文化价值),并产生了强烈感悟,才能享受数学学习乐趣、体会数学魅力.
参考文献:
[1]刘发. 关注思维过程,突出数学思想方法——“勾股定理”教学设计与说明[J]. 基础教育论坛,2012(34):36-39.
[2]冯志远,蔡莹. 中小学生数学爱好培养丛书:必知的中国数学家[M]. 沈阳:辽海出版社,2010.
[3]白丽娜. “勾股定理”教学设计[J]. 中国数学教育,2018(09):26-32.
[4]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心. 义务教育教科书·数学·八年级·下册[M]. 北京:人民教育出版社,2013.

