课程视域下的初中数学单元作业设计

金国成

［摘  要］ 在实践操作中，某些教师由于对作业属性的偏见，在设计与研制过程中缺乏理性的行为，导致作业成为学生的负担. 所以要减轻学生的作业负担，可以从属性上重新认识作业，在课程视域下重新构想作业的研制与设计，让作业回归“学习”本质，让学生在参与中提升学习力.

［关键词］ 课程视域；初中数学；单元作业；平行四边形

近年来，随着“双减”政策及《中共中央国务院关于深化教育教学改革全面提高义务教育质量的意见》的全面铺开，日常教學中耳熟能详的“作业设计”的进一步革新势在必行. 如何打破固有的认知，回归作业设计本质？如何实现跨学科作业设计，达到更优的教学效果？如何完善作业的评改方式？……这一系列问题在笔者脑海中徘徊.

基于此，笔者翻开了上海市教育委员会教学研究室副主任王月芬所著的《重构作业：课程视域下的单元作业》一书，希望能充实理论知识，从中探寻到作业设计的突破口.

什么是课程视域

杭州师范大学张华教授说道：“在理论界存在着两批专业人员、两个研究领域，这就形成了课程论专家与课程研究领域、教学论专家与教学研究领域，并分别积累了大量研究成果. ”张教授说的两个研究领域就是指“课程视域”和“教学视域”，两者既有联系，又有区别.

课程视域强调的是从学生的角度出发，关注“需要培养怎样的学生”“通过怎样的途径来培养学生”“怎样判断学生学习的目标达到哪个层次并进行反思调整”等问题. 课程视域是一种科学的研究方法，注重根据学生的学习表现和结果，对设定的目标进行反思和调整，以逐步完善目标. 因此，课程视域的主要表现是：目标设定、内容选择、整体思考、反思调整［1］.

教学视域强调的是从设定的教学目标和教学内容出发，关注的是怎样进行有效的教学，而教学过程中的各种巧妙方法与技巧是关注的重点，即更加关注教师的教，强调教师在教学过程中目标的实现和方法技术等.

从上面的论述我们可以发现，与教学视域相比，课程视域更具有创造性和灵动性，可以展现学生的个体性和灵活性.

课程视域与初中数学单元作业

（一）初中数学单元作业

初中数学单元作业，是课程视域下作业观的一个具体操作载体. 初中数学单元，一般指的是教材的自然单元、跨自然单元、思想方法单元（主要是素养目标或核心能力等）、项目单元（主要是跨学科或学科传统文化等）. 在这样的理念下，初中数学单元作业可以是课时作业的累加、单元整体的综合应用、跨学科等，或是以上形式的多种组合.

（二）初中数学单元作业的特征和价值

课程视域下的初中数学单元作业设计是教师以单元为载体，依据单元目标，以重组、改编、研发等多种形式进行单元作业的设计. 由此可见，单元作业体现了数学知识的结构性、整体性、典型性和层次性. 这是单元作业的优势，也体现了单元作业具有课程视域的特征.

课程视域下的初中数学单元作

业设计路径及实施

（一）分析单元编写意图

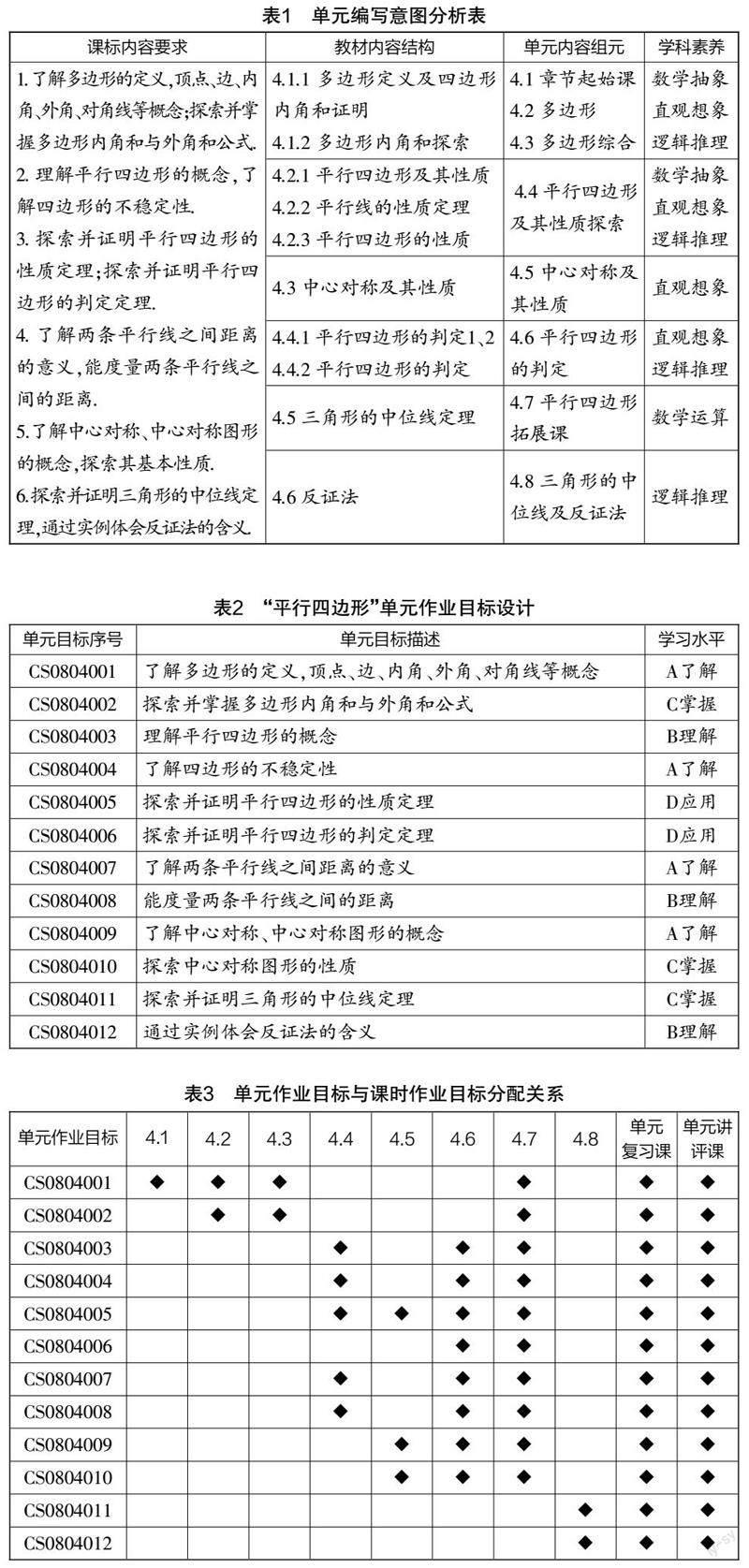
结合《义务教育数学课程标准（2022年版）》和浙教版教材，可分析出“平行四边形”这一单元的课标内容要求、教材内容结构与学科素养等  ［2］ （如表1所示）.

（二）明确单元作业目标

单元作业目标设计有助于教师理解和操作，是体现课程视域思想的作业目标设计方式. 表2是“平行四边形”的单元作业目标设计.

（三）分配单元作业目标

单元作业目标设计好之后，教师就可以将其分配或分解到课时作业目标中. 单元作业目标分配到各个课时并不是简单机械的，有些单元作业目标可以分配到几个课时甚至所有课时. 为了便于理解和操作，笔者设计了单元作业目标和课时作业目标形成分配关系，如表3所示.

（四）科学优化作业内容

本文所述的初中数学单元作业设计是站在课程视域下，以单元为视角，从整体出发，并依托《嘉兴市初中数学作业设计与实施建议》来进行的. 下面，笔者从几个方面来进行单元作业设计.

1. 基础巩固型作业——精

“基础巩固型作业”主要用于帮助学生习得“双基”，巩固基础知识，训练基本技能. 在“双减”政策背景下，基础巩固型作业更要体现出“精”，即精练学生的练习作业，并适当补充回顾与梳理数学知识产生与发展过程的作业及理解数学知识本质的作业.

（1）回顾与梳理数学知识产生与发展过程的作业

例1  作图①：如图1所示，将△ABO绕点O旋转180°后得到△CDO，点A，B的对应点分别为C，D，连接AD，BC，得四边形ABCD；

作图②：如图2所示，在平行四边形ABCD中，O是对角线AC与BD的交点，M是AB的中点，标出点M关于点O的对称点N的位置.

设计意图  让学生感受到知识的前后联系，引导学生快速梳理知识脉络，建构知识网络，让学生加深对知识本质的理解，培养结构化思维.

（2）理解数学知识的本质

例2  如图3所示，已知平面内A，B，C三点，请用多种方法画出平行四边形ABCD，并解释画法的合理性.

设计意图  有利于学生进一步理解平行四边形的判定方法，加深对知识本质的理解，培养学生的结构化思维.

2. 能力拓展型作业——实

“能力拓展型作业”对发展学生的数学学习能力有重要作用，它主要指发展学生认知能力和数学核心能力的作业. 这些能力将影响学生后续学习的潜力，甚至伴随学生终生，故这类作业要体现出“实”.

例3  如图4所示，在平行四边形ABCD中，E，F两点在对角线AC上，且AE=CF，连接DE，EB，BF，FD，求证：四边形DEBF是平行四边形.

变式1  如图5所示，在平行四边形ABCD中，连接BD，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F，连接CE，AF，求证：四边形AECF是平行四边形.

变式2  如图6所示，在平行四边形ABCD中，E，F两点在对角线AC的延长线上，且AE=CF，连接BE，BF，DE，DF，求證：四边形BFDE是平行四边形.

变式3  如图7所示，在平行四边形ABCD中，M，N两点分别在AD，BC上，E，F两点均在对角线AC上，且DM=BN，AE=CF，求证：四边形MENF是平行四边形.

设计意图  通过变式训练，展示演变过程，帮助学生理清知识之间的内在联系，提高学生一题多变、一题多解的能力.

3. 应用探究型作业——明

“应用探究型作业”指向发展学生解决数学问题的能力，主要指学生迁移、运用数学基础知识、基本技能、基本思想、基本方法，解决综合性强的数学问题的作业. 故这类作业要体现出“明”的思维方式.

例4  如图8所示，在平行四边形ABCD中，E，F两点分别在边BC，AD上，且AF=CE，连接EF. 请你只用无刻度的直尺确定线段EF的中点O，并说明理由.

变式1  如图9所示，在平行四边形ABCD中，E，F两点分别在边BC，AD上，且AF=CE，直线EF分别与AB的延长线和CD的延长线交于点H和点G，求证：H，G两点关于EF的中点O对称.

变式2  如图10所示，在平行四边形ABCD中，E为边BC的中点，F为边CD上一点，DE与AF相交于点G，过点C作CH∥AF交DE于点H，判断DG与EH的数量关系并说明理由.

设计意图  既有利于学生进一步理解平行四边形的中心对称性质，又有助于培养学生的合情推理能力，还能发展学生的逻辑思维能力与推理论证能力.

4. 综合实践型作业——趣

“综合实践型作业”指向发展学生解决生活实际问题的能力，主要指学生综合运用数学学科和其他学科的知识与方法解决真实世界中的问题，促进学生对数学学科的理解和跨学科知识的获得，培养学生的创新意识、实践能力、社会担当等综合品质，促进数学学科育人方式和学习方式的根本变革. 故这类作业要体现出作业的“趣”.

例5  刚学完“平行四边形”这一章，教师便给学生布置了一个绘制章节思维导图的作业，要求学生尽量归纳、总结本章节所学的概念、判定方法、数学模型、学习体会等.

设计意图  思维导图能从提炼重点、归纳总结、发散思维、联想和创新等方面，培养学生的高阶思维能力.

例6  请同学们利用轴对称和中心对称的知识，剪出美丽的窗花，让家里福气满满，记得拍照留存.

设计意图  寓教于乐，让每一个学生在实践中增长知识、提升能力，培养学生的创新意识、实践能力.

（五）单元作业管理反馈

课程视域下的初中数学单元作业设计与以前的作业设计相比，是有进步的，但是教师如何更好地对作业进行管理并反馈等一直困扰着笔者. “双减”文件明确要求学校要将作业设计纳入教研体系，同时各级教研部门要加强专业指导，定期开展作业相关培训，完善学校作业统筹和规划机制，确保一校一策. 学校定期组织教研组、备课组学习课标，明确作业设计标准，规范作业编制流程，依据作业质量相关属性及要素，研制作业规划细目表，落实学校、年级、备课组作业库的建立.

所以教师要创新使用作业，有选择地、灵活地使用作业，并适当调整，使作业符合本班学情. 学校教务处可定期公示作业制度. 笔者所在学校在浙江省的相关文件指导要求下，尝试探索每周一天“无作业日”，减少周末、法定节假日作业，尝试每月一个“无作业周末”. 教师每周填写“作业统筹表”，创新作业评价反馈机制，年级组统筹作业总量，学科组加强校本教研，提升校本作业质量，落实促进教学水平及学校发展的作业反馈评价机制.

设计作业的过程也是全面育人的过程，教师要充分发挥作业的价值，优化单元作业设计能力，让学生在做作业的过程中锻炼“思维”，增长“智慧”.

参考文献：

［1］王月芬. 重构作业：课程视域下的单元作业［M］. 北京：教育科学出版社，2021.

［2］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.