螺母丝杠机构的静力学仿真及可靠性分析

卜庆伟,米 洁,张胜伦,薛 冰

(北京信息科技大学机电工程学院,北京 100192)

螺母丝杠传动副是典型传动机构,又称螺旋传动机构[1]。在工作过程中,螺母丝杠传动副将旋转运动变为直线运动,并传递运动和力。对螺母丝杠机构而言,在其工作运行过程中,螺母轮齿一直处于啮合状态,而丝杠螺纹与螺母交替啮合,因此丝杠螺纹的啮合时间仅为螺母螺纹的1/90左右,使得在螺母丝杠的使用寿命周期内,螺母为易损件。近年来,提高机械部件磨损可靠性的研究越来越受到国内外的广泛重视。由文献[2]对螺母丝杠的失效机理分析可知,磨损是螺母丝杠传动机构最主要的失效模式。因此,研究其磨损可靠性对改进螺母丝杠传动副的设计和寿命预测具有重要意义。本文对螺母丝杠磨损可靠性进行研究,首先基于螺母丝杠的轮齿强度标准校核螺母丝杠轮齿的剪切强度和弯曲强度,同时考虑工况和材料等参数的不确定性,建立螺母丝杠轮齿的许用磨损量的数学模型;然后基于Archard模型[3],结合螺母丝杠有限元仿真分析,考虑滑动距离、法向载荷等参数的不确定性,建立螺母丝杠轮齿实际磨损量的数学模型;接着利用蒙特卡洛法[4]得到许用磨损量与实际磨损量的分布形式,通过应力强度干涉法建立螺母丝杠磨损可靠性模型;最后通过分析、计算得出螺母丝杠机构的磨损可靠度。

1 螺母丝杠机构

螺母丝杠螺旋副传动为传动原理的一种[5]。螺母丝杠组件由外壳、丝杠和螺母组成,螺母分别与丝杠、外壳互相啮合,图1所示为其结构图。

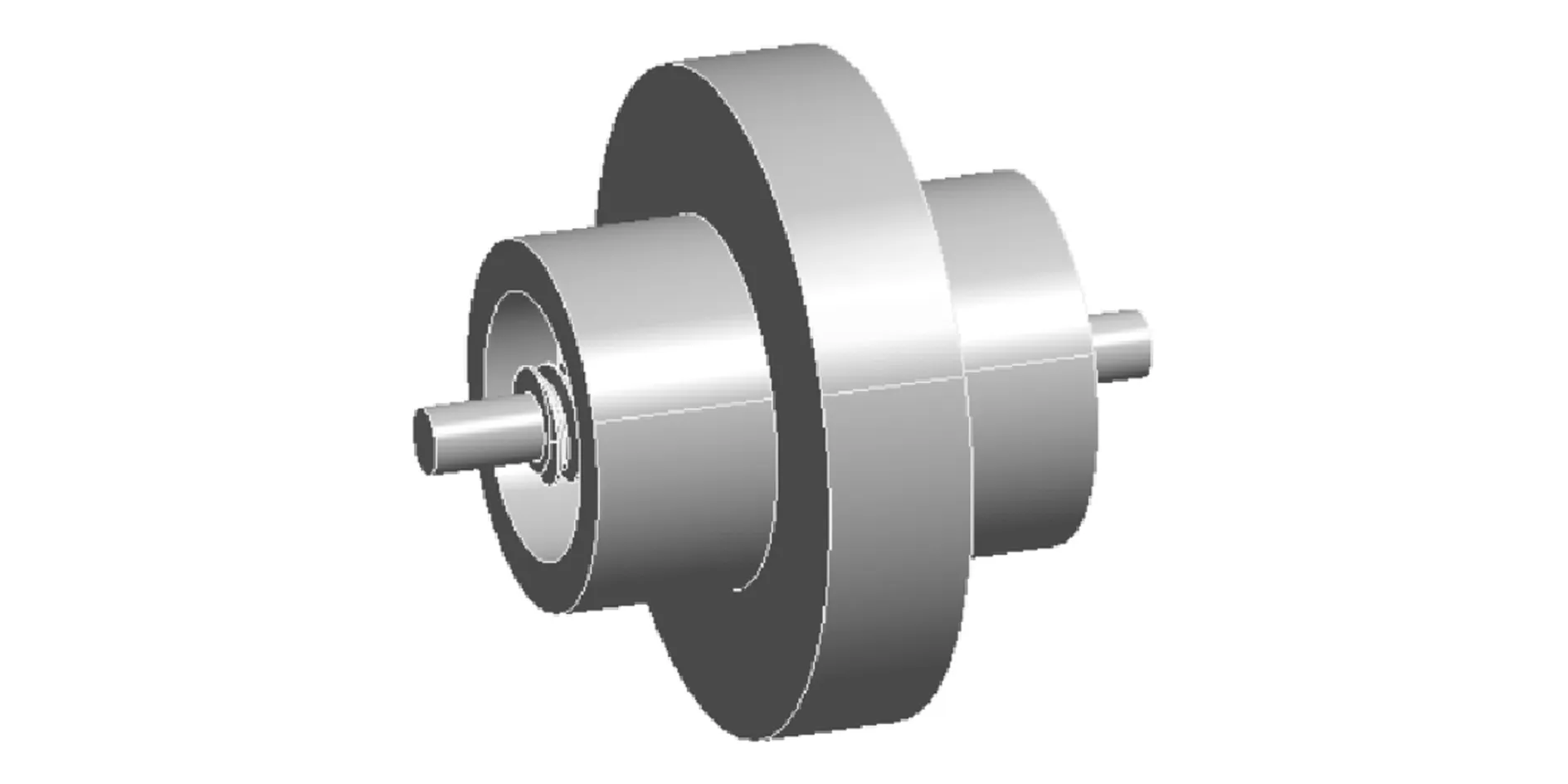
图1 螺母丝杠组件结构图

2 螺母丝杠静力学仿真分析

2.1 模型导入及设置

螺母丝杠静力学仿真模型如图2所示。首先定义坐标参考系,定义x轴方向为平行于丝杠的方向,定义y轴、z轴方向为垂直于丝杠的方向;然后将螺母丝杠模型导入ANSYS Workbench仿真软件中。

图2 螺母丝杠网格模型

2.2 划分网格

在螺母与外壳、螺母与丝杠的接触区域,设置整体网格尺寸为1.5 mm,并设置所有表面的网格尺寸为1.0 mm。由于螺母的螺纹啮合部位为主要分析部位,因此对螺母与外壳、螺母与丝杠的接触表面设置膨胀层,法向层数为4层,最大厚度为1.0 mm。调整后的最终网格如图3所示,共划分出693 557个节点、354 019个单元,整体网格的平均雅可比为1.322 3,平均偏度为0.430 47。

图3 约束方式示意图

2.3 边界条件和载荷设置

根据螺母丝杠的实际工况[6],将螺母轴向固定,仅发生旋转运动,释放螺母z轴方向的转动自由度,丝杠为从动件。在静力接触仿真中设置固定约束,模型约束方式如图3所示。

模型的驱动力为螺母受到的转矩,根据文献[7]添加平均载荷737 N,通过计算得到螺母转矩为2 422.5 N·mm。载荷施加方式如图4所示。

图4 载荷施加示意图

2.4 网格无关性验证

为确保仿真结果的准确性,减少网格划分质量对求解结果的影响,本文采用网格无关性验证:首先采取多种网格划分方法分成若干仿真组,然后对每个仿真组添加相同的载荷、约束边界,验证求解结果与网格划分尺寸无相关性。

不设置网格划分选项,进行网格自动划分,对应仿真序号1。选择1.3～2.3 mm的网格尺寸区间,改变划分网格的尺寸,以0.2 mm为一个间隔,分为6组,对应仿真序号2～7。记录每组仿真的单元特征长度平均值、节点数、单元数、应力应变结果。其中,一个单元的特征长度是该单元体积的立方根,是评价单元大小的方式之一,单元平均特征长度即所有单元的特征长度的平均值。网格无关性验证结果见表1。

表1 无关性验证表

将表1的应力、应变结果作为纵坐标,仿真序号作为横坐标,绘制折线图,如图5所示。

图5 螺母丝杠网格无关性验证结果图

由结果可得,仿真进行到第3组之后,即设定的网格划分尺寸小于1.9 mm,仿真结果呈现规律波动,可以认为此时仿真结果基本趋于稳定。

2.5 仿真结果分析

丝杠、螺母、外壳的仿真结果如图6～图8所示。为了方便观察,螺母丝杠构件做了半剖处理。由图可知,模型的应力最大值位于螺纹的旋入侧,其中驱动方向螺纹的应力水平最高,沿x方向螺纹的应力水平依次降低,模型的最大变形为螺母的旋转变形,与螺旋传动的工况相符。

图6 外壳-螺母-丝杠的应力、应变分布云图

图7 丝杠的应力、应变、位移分布云图

图8 外壳的静力分析应力、应变、位移分布云图

3 考虑不确定性螺母丝杠可靠性分析

3.1 螺母丝杠可靠性分析流程

螺母丝杠可靠性分析流程图如图9所示。

图9 螺母丝杠可靠性分析流程图

3.2 螺母丝杠不确定性分析

从可靠性的角度来说,造成产品失效的量,在多数情况下不是定值,而是一个有着一定分布特征的随机数,因此在分析计算时,需要将环境、材料等参数随机化,输入可靠性分析模型计算可靠度,进行不确定性分析,得到关键参数的分布特征。考虑到材料参数、实际工况、受力载荷的随机性会对应力应变有影响,因此选择密度、杨氏模量、泊松比、摩擦系数、受力载荷 5个参数作为不确定性分析随机输入变量,以截尾正态分布的形式表征,得到密度、杨氏模量、泊松比、摩擦系数、受力载荷的正态分布数值。在设定的分布区间对输入参数进行抽样,抽样方式选择拉丁超立方抽样方法(Latin hyercube),先对抽样空间(参数空间)进行分层,使每层的概率密度函数相等,在参数空间中各参数的层相交形成超立方。再对每个超立方进行筛选,使每个超立方的坐标互不重叠。最后通过抽样拟合得出变量的分布形式及分布特征。螺母丝杠不确定性分析的输入变量见表2。

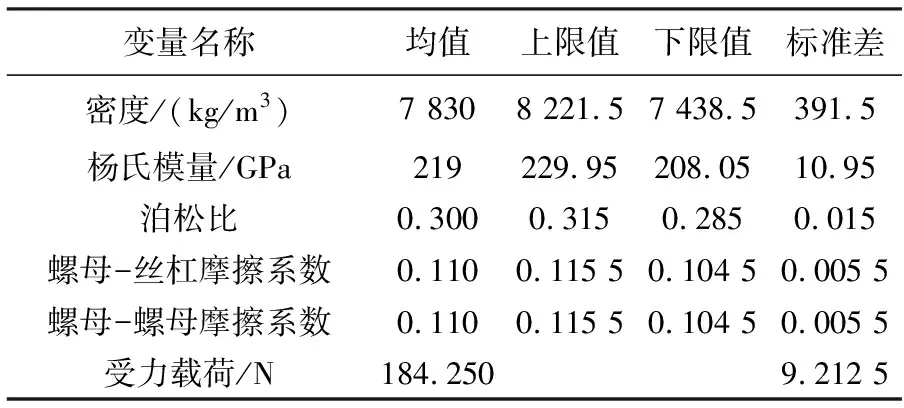
表2 不确定性分析输入变量分布特征

在设定的分布区间对输入参数进行抽样,经过计算拟合后,将分析得到的应力应变、滑移距离、接触正压力结果进行统计拟合,结果如图10、图11所示,由图可知,各参数的分布与结构基本服从正态分布。

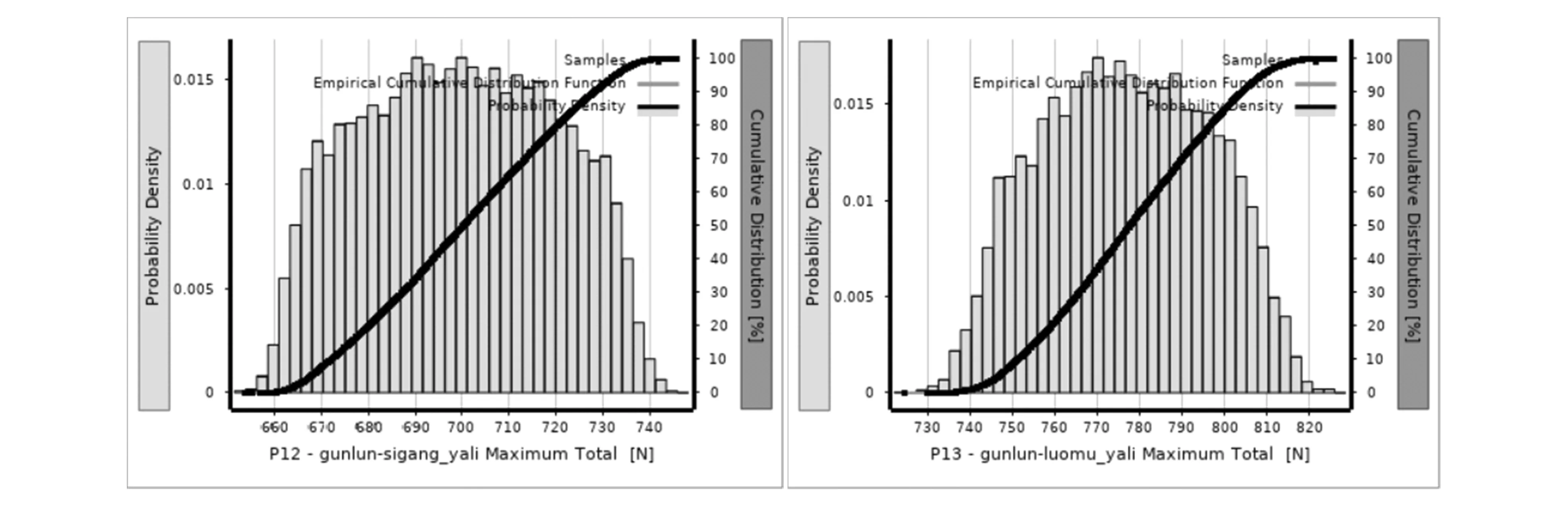
图11 螺母-丝杠与外壳-螺母正压力分布拟合结果

3.3 许用磨损量计算模型

由于螺母磨损主要导致轮齿齿根宽度b和齿顶宽度a减小,公称直径d和啮合齿数Z变化很小,因此可建立a、b与轮齿的剪切强度和弯曲强度的关系,并根据轮齿的许用剪切强度和弯曲强度推导出a、b的许用值。

根据文献[2]可知,符合轮齿强度要求的最小值(a+b)′为:

(1)

式中:F为轮齿啮合面的法向力,h为齿根高,α为两螺母啮合弧长对应角,[τ]为许用剪切强度,[σb]为许用弯曲强度。

(2)

式中:d2为啮合直径。

则螺母轮齿的许用磨损量Wmax为:

Wmax=(a+b)-(a+b)′

(3)

3.4 实际磨损量计算模型

目前,对轮齿磨损量的数值计算技术普遍基于archard磨损模型[3],如式(4)所示:

(4)

式中:V为材料的体积磨损量,s为螺母啮合齿面滑移距离,W为轮齿间的法向载荷,H为轮齿表面的材料硬度,K为磨损系数。其中K与润滑状态和磨损机理有关,可通过实验数据进行拟合与修正,使计算值更符合实际情况。

s可以通过式(5)计算:

s=ns′

(5)

式中:s′为螺母旋转一周啮合齿面的滑移距离,n为螺母旋转圈数。由于螺母每转动一周分别与螺母、丝杠啮合一次,所以s′可以通过式(6)计算:

s′=s1+s2

(6)

式中:s1、s2分别为螺母旋转一周螺母-丝杠啮合齿面和螺母-螺母啮合齿面的滑移距离。

n可以通过式(7)计算:

(7)

式中:xz为丝杠总行程,p为螺纹导程。

则archard磨损模型可变换为:

(8)

式中:W1、W2分别为螺母-丝杠啮合轮齿间的法向载荷、螺母-螺母啮合轮齿间的法向载荷。

若轮齿为均匀磨损,则磨损厚度(a+b)″可以通过式(9)求得:

(9)

式中:ΔV为磨损体积,A为磨损接触面表面积,L为啮合长度。

由此可以算出螺母磨损后的剩余厚度W″为:

W″=(a+b)-(a+b)″

(10)

3.5 螺母丝杠可靠度计算模型

输入参数的随机性,使得螺母的许用磨损量与实际磨损量均为随机分布,两者分布区间的干涉区域即为螺母丝杠的失效区域。若假设螺母的许用磨损量与实际磨损量符合正态分布,即Wmax～N(μ、σ2)、W″～N(μ′、σ′2),使用应力-强度干涉的方法计算螺母丝杠的可靠度P为:

(11)

式中:Φ(·)为标准正态概率分布函数,μ为许用应力均值,μ′为实际应力均值,σ为许用应力标准差,σ′为实际应力标准差。

3.6 可靠性分析

通过MATLAB仿真软件将随机变量及其分布特征输入疲劳可靠性模型,利用蒙特卡洛法对其进行5 000次仿真计算,拟合得到的许用磨损量Wmax分布形式如图12所示。

图12 许用磨损量分布曲线

分别设定行程为33 600、49 000 m,利用蒙特卡路法进行5 000次仿真计算,得到轮齿剩余厚度分布如图13所示。由图可知,在进入剧烈磨损期之前,螺母的剩余齿厚均值小于许用磨损量的均值。

图13 行程33 600、49 000 m实际磨损量分布图

为直观反映磨损过程中可靠度的变化情况,以总行程为横轴、可靠度为纵轴,使用应力强度干涉计算公式得到变化曲线,如图14所示。

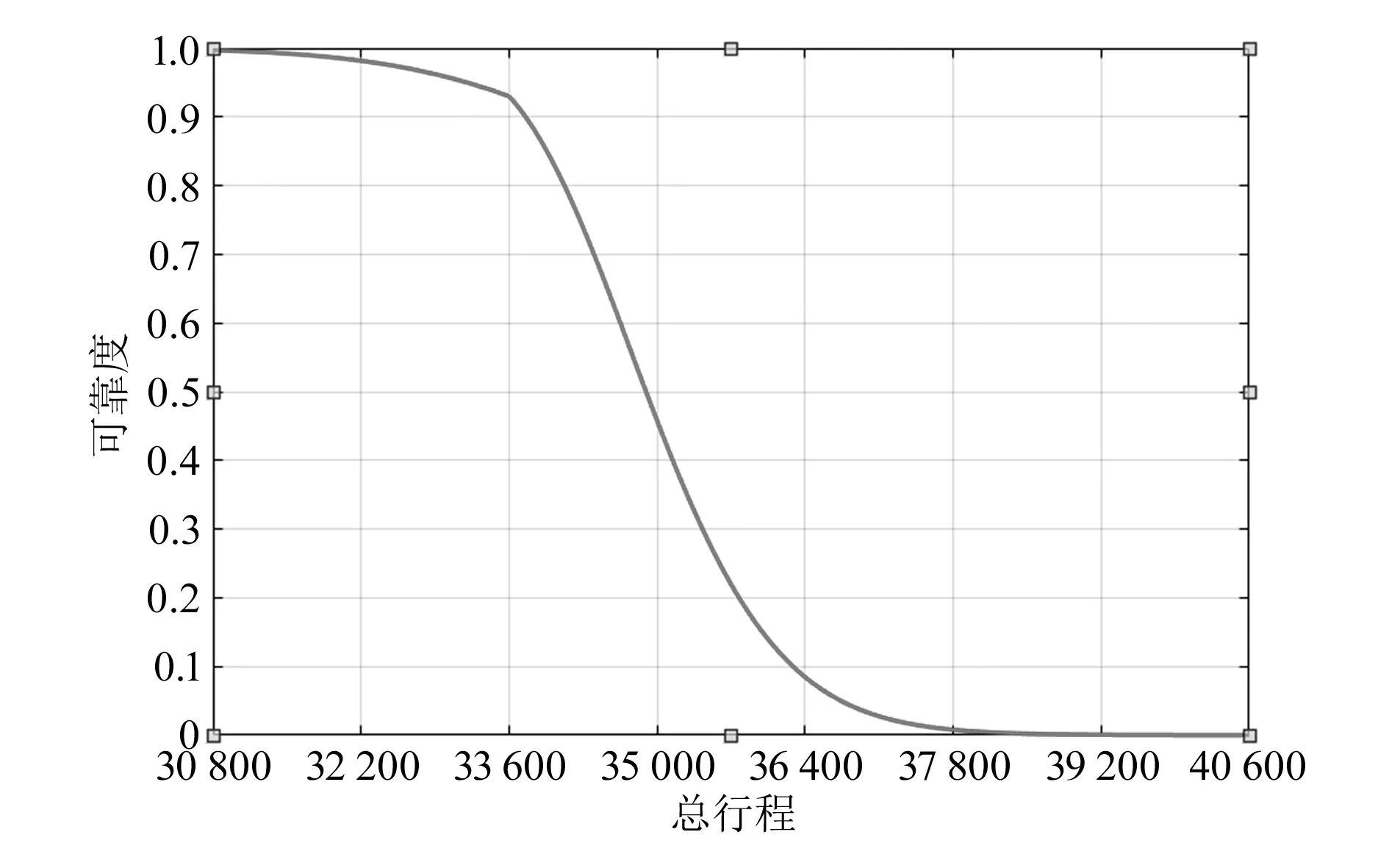
图14 螺母丝杠可靠度随总行程的变化曲线

4 结论

本文以螺母丝杠为研究对象,对其进行仿真分析和可靠性计算。结果显示:当丝杠行程增至31 500 m以上时,可靠度曲线开始下降;行程增至33 600 m时,可靠度降低至0.97左右,曲线开始快速下降;当行程增至36 400 m时,可靠度降低至0.12左右,此时曲线又开始缓慢下降;当行程增至38 500 m左右时,可靠度基本降低为0。由于可靠度快速降低的总行程只有2 800 m,因此在工程实际操作过程中,当行程增至33 600 m时,就要提高检修频率,必要时进行维修或更换,避免因可靠度降低导致的构件损坏。本文的研究可为螺母丝杠提升组件的优化设计提供理论指导,为检修工作提供理论依据。