基于双向航道与泊位资源协调的船舶调度优化

张明,任鸿翔,徐富权*,刘国威,周毅

1.福建船政交通职业学院航海学院,福建 福州 350007;2.大连海事大学航海学院,辽宁 大连 116026;3.中海油能源发展股份有限公司采油服务分公司,天津 300452

0 引言

随中国航运业的蓬勃发展,进出港口的船舶增多,吨位增大,港口业务日渐繁忙,航道资源日趋紧张。港口航道主要包括单向、双向和复式航道等模式。为提高航道的通过能力,可拓宽航道,由单向航道改为双向航道。双向航道的通航效率相对较高,但在船舶吃水受限,或双向通航需改为单向通航等情况下,船舶的调度优化受到较大影响。通常由港口调度中心和港口船舶交通管理中心2个部门制定港口的泊位分配和船舶进出港次序,在调度过程中,若能从整体上协调泊位资源和航道资源,可提高港口的调度效率和运营效率。

在双向航道的通航能力方面,王更等[1]建立深圳港铜鼓航道的仿真模型,验证其双向航行的通过能力;司文静等[2]分析双向通航水域的潮流、风、驾驶员等船舶操纵因素,基于排队论方法建立航道通过能力模型,计算航道的通过能力,通过实例验证模型精度;戴林伟[3]研究可变道航道,建立双向交通流元胞自动机模型,仿真研究允许和禁止变道情况下的船舶交通流,分析船舶到达率、船舶流量和平均航速间的关系。

在双向航道船舶调度方面,Sluiman[4]提出过境船舶双向航行的交通调度算法,限制船舶间的安全距离;郑红星等[5]研究双向通航的水域调度,考虑服务规则和夜航约束,建立混合整数调度模型,采用分支切割算法求解调度方案,满足调度需求;何春华[6]通过网格分割法规划双向通航水域,建立进出港船舶的大数据信息传递调度模型,依据数据特征调度并设计自适应融合算法;王亚辉等[7]船舶进出港大数据,仿真分析双向航道的通航能力,设计自适应算法,得到航道调度新策略;张新宇等[8]研究黄骅港双向航道交通问题,分割大型船舶的乘潮位置,构建船舶乘潮时间窗计算模型,提高大型船舶进港效率。

在港口泊位资源方面,Zhang等[9]对单向航道和泊位资源进行联合优化,建立多目标综合优化模型,提高船舶调度效率;Al-Refaie等[10]分析采用不同模型处理定期到达和紧急到达工况,得到船舶调度和泊位分配方案,明显减少延误成本;Liu等[11]针对单向航道港口提出混合整数线性规划模型,减少所有船舶的总等待时间(调度开始时刻减去船舶申请时刻的时间),设计自适应大邻域搜索算法,并通过京唐港数据进行验证;Zhang等[12]研究散货港码头作业和船舶调度的集成优化,考虑装卸作业、航行冲突等特殊情况,建立协同优化模型,通过改进的算法求解复杂模型,采用黄骅港数据验证模型的合理性;邰世文等[13]研究煤炭码头船舶和泊位的联合优化问题,仿真码头作业模式,以作业效率最高和在港时间最短为目标建立联合优化多目标模型,采用遗传算法求解;郑红星等[14-15]研究船舶进出港次序与泊位分配的协同优化问题,分别考虑单向航道、减载移泊和潮汐等影响,建立协调调度优化模型并设计相应的算法求解。

现有研究多以船舶在港总等待时间最短为目标,但影响港口船舶调度的因素较多,采用多目标优化更符合多方利益。随船舶大型化的发展,大船多需乘潮进港,泊位分配计划对船舶调度也有影响。从整体上集成优化港口资源可得到更高效的运营方案,提高港口业务能力。考虑单向航道的协调调度研究较多,对通航规则相对复杂的双向航道水域的协调调度研究较少。本文研究双向航道与泊位资源的协调优化问题,考虑双向通航限制、泊位类型和潮汐等影响因素,建立多目标集成优化模型,并设计智能优化算法求解调度方案,以期提高港口的运营效率。

1 问题描述与模型构建

1.1 问题描述

在双向航道港口调度中需考虑船舶类型、船舶吃水和船舶宽度等限制条件,确定航道通航规则。船舶进出港过程示意图如图1所示。满足双向通航规则的船舶,经船舶交通服务中心审批后可同时进入航道;若未通过审批,进港船舶需在锚地等待调度,出港船舶需在泊位等待调度;遇到航行限制时,需考虑将双向航道改为单向航道。频繁改变通航模式将延误港口运营,需制定合理高效的调度方案。根据码头布局,主要有离散型和连续型2种泊位,采用离散型泊位的港口较多[16],均已固定港池水深和岸线长度,泊位有明确的服务船舶类型,制定船舶进出港计划时应提前完成泊位资源分配。制定调度方案时,减少船舶等待时间可提高港口业务量,减少船舶调度时间可提高航道利用率。

图1 船舶进出港过程示意图

双向航道和泊位资源的协调优化问题可描述为:具有离散型泊位的港口,在己知船舶类型、船舶预计到港和离港时刻等相关信息的前提下,考虑大船乘潮进出港、通航规则转换等现实条件,兼顾进出港船舶的服务时间、航行安全的时空间约束,以船舶总调度时间、总等待时间最短为目标,建立协调调度模型,得到更高效的船舶进出港调度方案。

1.2 双向航道与泊位资源协调优化模型

对模型设置假设:1)港口水域气象条件,港口拖轮、泊位和锚地等资源均符合双向航道调度要求;2)已知各船舶进出港申请时间,船舶在泊位或锚地等待调度;3)港池内为离散型泊位,且泊位有对应服务船舶类型;4)分配泊位时需考虑船舶吃水、船舶类型和船舶长度等基本属性;5)船舶以恒定速度在航道航行,禁止在航道中追越其他船舶。

建立双向航道与泊位资源协调优化模型的目标函数为:

min [Z1,Z2],

式中:Z1为船舶总调度时间,Z2为船舶总等待时间。其中,

Z1=Te,max-Ts,min,Te,max≥Te,i,Ts,min≤Ts,i,∀i∈I,

(1)

(2)

式中:Te,max为所有船舶调度结束的最晚时刻;Ts,min为所有船舶调度开始的最早时刻;Te,i为船舶i调度的结束时刻,i为船舶编号,i∈I={1,2,…,n},其中I为进出港的船舶集合,n为当前调度阶段的船舶总数;Ts,i为船舶i调度的开始时刻;Ta,i为船舶i申请进出港的时刻。

模型约束条件中,所有船舶都有泊位可靠泊,可表示为:

式中:Xi为船舶i是否存在类型匹配的空闲泊位,Xi=0为无可用泊位,Xi=1为存在可用泊位。

船舶的调度开始时刻不得早于船舶申请时刻,可表示为:

Ts,i-Ta,i≥0,∀i∈I。

船舶调度结束时刻限制为:

Te,i-Ts,i-Tb,ij-d1/vi≥0,∀i∈I,j∈J,

式中:J为可用的泊位集合,j为泊位编号,j∈J={1,2,…,m},m为港内泊位数;Tb,ij为船舶i从泊位j到航道入口的航行时间;d1为航道长;vi为船舶i在港内的平均航速。

受双向航道航行规则约束,当视程不佳时,转换为单向通航模式,可表示为:

式中:NM,i为船舶i的通航模式,NM,i=0为单向通航,NM,i=1为双向通航;V为能见度;V0为航道双向通航时限制视程。

受双向航道航行规则约束,当风力较大时,转换至单向通航模式,可表示为:

式中:W为风力等级,W0为航道双向通航时限制风力。

受双向航道航行规则约束,当船宽较大时,转换至单向通航模式,可表示为:

式中:Ws,i为船舶i的宽度,B1为航道双向通航时单船限制船宽。

受双向航道航行规则约束,当两船宽之和较大时,转换至单向通航模式,可表示为:

式中:B2为双向通航时相对航行的两船船宽之和限值;i′为除i以外任意船舶编号,i≠i′,且i,i′∈I={1,2,…,n}。

所有需乘潮进出港船舶须选择乘潮时间段,乘潮船舶应在理论乘潮时间段内占用航道,公式为:

Nts,i-Sp-M(1-Ni,p)≥0,∀i∈I,∀p∈Tp,

Nte,i-Ep-M(1-Ni,p)≤0,∀i∈I,∀p∈Tp,

式中:Cs,i为船舶i是否需乘潮进出港,Cs,i=0时无需乘潮,Cs,i=1时需乘潮;Ni,p为船舶i是否选择乘潮时间段,Ni,p=0为船舶i未选择乘潮时间段p进出港,Ni,p=1为船舶i选择乘潮时间段p进出港;M为极大的正数;Nts,i为大型船舶i在安全的乘潮航行时间窗内的开始时刻;Nte,i为大型船舶i在安全的乘潮航行时间窗内的结束时刻;Tp为所有乘潮时间段的集合,p为乘潮时间段的编号;Sp为大型船舶乘潮时间段p的开始时刻;Ep为大型船舶乘潮时间段p的结束时刻。

受船舶调度开始时刻的约束,按次序计算船舶调度时刻,若相邻两艘船舶均为进港船,可表示为:

Ts,i′=max(Ta,i′,Ts,i+d2/vi+Tf,i′-d2/vi′),Aii′=1,∀i,i′∈I,

式中:Aii′为船舶i与船舶i′的调度前后次序,Aii′=0时船舶i在船舶i′后进入航道,Aii′=1时船舶i在船舶i′前进入航道;Tf,i为船舶i与同向行驶船舶的安全间隔时间;d2为锚地至航道入口的距离。

若相邻两艘船舶均为出港船,可表示为:

Ts,i′=max(Ta,i′,Ts,i+Tb,ij+Tf,i′-Tb,i′j′),Aii′=1,∀i,i′∈I,j,j′∈J,

式中j′为除j以外的任意泊位编号,j≠j′且j,j′∈J={1,2,…,m}。

若相邻两艘船舶异向航行,后船为出港船,可表示为:

Ts,i′=max(Ta,i′,Te,i-Tb,ij+Tf,i′-Tb,i′j′),Aii′=1,NMi=0,∀i,i′∈I,j,j′∈J。

若相邻两艘船舶异向航行,后船为进港船,可表示为:

Ts,i′=max(Ta,i′,Te,i+Tf,i′-d2/vi′),Aii′=1,∀i,i′∈I。

受航道上禁止追越限制,可表示为:

vc,i-vc,i′≥0,Aii′=1,∀i,i′∈I,

式中:vc,i为船舶i在航道的航速,vc,i′为船舶i′在航道的航速。

受泊位分配约束,依照泊位类型、泊位长度和泊位水深进行约束,可表示为:

M(Kb,j-Ks,i)=0,∀i∈I,j∈J,

Io,i(Lb,j-Ls,i)M>0,∀i∈I,j∈J,

Io,i(Db,j-Ds,i)M>0,∀i∈I,j∈J,

式中:Kb,j为泊位j的类型;Ks,i为船舶i的类型;Io,i为船舶i的进出港航行方向,Io,i=0时为出港,Io,i=1时为进港;Lb,j为泊位j的长度;Ls,i为船舶i的长度;Db,j为泊位j的水深;Ds,i为船舶i的吃水深度。

选择同一泊位的出港船舶调度应早于靠泊该泊位的进港船舶,可表示为:

Aii′-MIo,i>0,∀i∈I,j∈J。

在调度前,进港船靠泊的泊位应为空闲状态,可表示为:

Io,i-MBo,j>0,∀i∈I,j∈J,

式中:Bo,j为泊位j是否空闲,Bo,j=0时泊位空闲,Bo,j=1时泊位已被使用。

决策变量取值范围为NMi,Cs,i,Ni,p,Io,i,Bo,j,Aii′,Xi∈{0,1},∀i,i′∈I,j∈J。

2 算法设计

船舶进出港调度优化问题属于非确定性多项式问题,双向航道与泊位资源协调优化模型包含多个复杂约束,难以通过精确算法或专业求解器求解,可采用智能优化算法进行求解。NSGA-II算法常用于求解多目标优化问题,运行速度较快、结果收敛性较好,但解集随机性较高,解的质量较差,直接应用于模型求解效果不佳。根据双向航道和泊位资源协调调度问题的特点,改进NSGA-II算法,设计种群初始化策略、新个体生产策略,并引入自适应交叉及变异概率,改进后的算法流程如图2所示,分为9步。

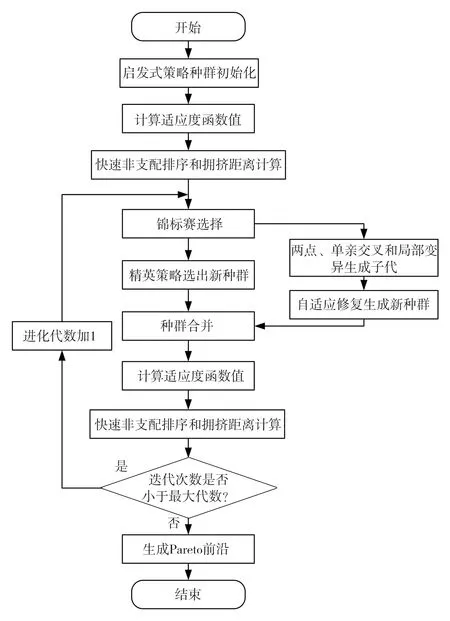
图2 改进后NSGA-II算法流程图

1)根据航道、船舶和泊位等数据设置初始化参数。

2)将船舶调度次序和泊位分配编码分别置于2层循环中,在内部循环中制定进港船舶和出港船舶的调度顺序,考虑船舶出港后有泊位空闲,在外部循环中接收更新后的空闲泊位信息,制定泊位分配方案,产生大小为2N的初代种群,N为种群规模。

3)对初代种群进行编码,见图3。

图3 编码示意图

由图3可知:有3层染色体结构层,第1层为船舶出港次序,4号出港船调度次序在3号出港船前;第2层为船舶进港次序,2号进港船调度次序位于5号船舶后;第3层为对应船舶泊位,8号进港船舶对应5号泊位。满足双向通航条件时,3号和5号船舶同时进出港作业,否则需等待上艘船舶航行结束后,3号船舶再进入航道。计算适应度,适应度函数分别取式(1)(2)的倒数。

4)对初代种群进行非支配排序和拥挤距离计算。

5)采用精英策略选择N个优秀个体组成新种群。

6)采用单亲交叉、两点交叉和局部变异产生N个新个体,单亲交叉过程、两点交叉过程和局部变异过程如图4～6所示。

图4 单亲交叉示意图

图5 两点交叉示意图

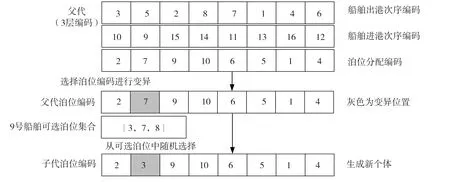
图6 局部变异过程示意图

7)通过遗传操作产生的新种群与每次迭代保存的父代种群合并,得到新一代种群。

8)对新一代种群进行非支配排序和拥挤距离计算。

9)若满足算法终止条件,输出所有非支配排序层为1的解;若不满足终止条件,进化代数加1后,转至步骤5进行循环。

为避免算法陷入局部最优,引入自适应交叉和变异概率,随种群发展变异概率P改变。若出现个体向同一方向发展,此时需增大P;反之需减小P,保证优等个体生存。自适应交叉与变异概率

式中:Pmax为最大交叉概率,Pmin为最小交叉概率,f为当前个体的适应度,favg为种群平均适应度,fmax为最大适应度。

3 算例分析

以我国北方某港口为例,验证第2节的多目标求解算法在解决双向航道与泊位资源协调优化问题的有效性和优越性。该港口有一、二、三号港外锚地,3个锚地距航道口分别为3、7、9 n mile,双向通航,航道长d1=8 n mile,规定若单船宽度大于45 m或相向航行的船舶宽度之和大于75 m,需实行单向通航。航道水深有限,超大型船舶需乘潮进出港。港口共有20个离散型泊位,具体泊位信息如表1所示。进出港船舶信息如表2所示,该阶段需完成调度20艘船舶,包含12艘进港船舶和8艘出港船舶,2号和12号船舶需乘潮进出港。

表1 港口泊位信息

表2 进出港口船舶信息

3.1 有效性分析

采用MATLAB 2020a运行算法,设置最大遗传代数为200,种群规模为200,交叉和变异概率分别为0.9、0.1,得到的Pareto前沿解集如图7所示。其中图中加黑圆圈点解的调度计划为:该阶段所有船舶Z1=382.2 min,Z2=893.4 min;12艘进港船舶调度次序、时间节点和泊位分配计划如表3所示。12号船舶使用航道时间窗为[140.0, 199.3],满足其理论需乘潮汐的时间窗[140.0,280.0]。8艘出港船舶调度次序和时间节点如表4所示。2号船舶需乘潮汐的时间窗为[150.0,270.0],使用航道时间窗为[206.7, 266.0],可安全进出航道。由表3、4可知:泊位分配计划满足船舶自身条件,需保持安全会遇形势的2号、12号、14号船舶(船宽较大,单向通航)均采用单向通航模式,调整其他船舶在航道中的航速,未出现追越局面。因此,多目标求解算法适用于双向航道与泊位资源协调优化问题,可得到有效最优解。

表3 进港船舶调度计划

表4 出港船舶调度计划

图7 Pareto前沿解集

3.2 算法优越性分析

多目标优化模型的Z1收敛过程如图8a)所示,Z2收敛过程如图8b)所示。由图8可知,在200次迭代寻优过程中改进的NSGA-II算法稳定性较好。

a)Z1 b)Z2 图8 优化目标收敛曲线

为验证改进后NSGA-II算法的优越性,设置不同规模的算例分别求解,结果如表5所示。由表5可知:随船舶数n、泊位数m及单向通航船舶数的变化,改进后NSGA-II算法在Z1和Z2的寻优效果和算法运行时间方面均优于NSGA-II算法。

表5 不同算例和2种算法下2个目标的优化对比

通常以人工方式进行港口的船舶调度,遵循先到先服务规则或大船优先服务规则,实时制定调度方案,受外在因素干扰较多,调度效率较低。对北方某港口遵循先到先服务规则进行调度,基于表1、2的信息,Z1=539.5 min,Z2=2 836.8 min。采用改进后NSGA-II算法求解的调度方案Z1=382.2 min,Z2=893.4 min,分别缩短了29.2%和68.5%,船舶进出港调度效率显著提升。

4 结束语

研究具有离散型泊位的双向航道港口船舶的进出港调度优化问题,建立双向航道与泊位资源协调的多目标优化模型,采用改进后NSGA-II算法优化协调双向航道与泊位资源,在目标寻优和求解时间方面均优于NSGA-II算法。与先到先服务调度方案相比,多目标优化模型求解得到的调度方案大幅度提高港口船舶调度效率。

但多目标优化模型未考虑拖轮、岸桥等资源整合,下一步研究可同时整合港内资源。调度模型亦可融入泊位作业效率、船舶油耗等经济因素,以期得到全面高效的调度方案。