基于改进双重无迹卡尔曼滤波算法的车辆状态估计

费明哲,王健*,于金鹏,杨君,杜若飞,王云靖,邓欢

1.山东交通学院汽车工程学院,山东 济南 250357;2.青岛大学自动化学院,山东 青岛 266071

0 引言

车辆运行时,从反馈参数中获取精确、实时的状态信息是提高车辆主动安全控制能力的重要保证,随无人驾驶技术的发展,状态估计和参数估计越来越重要,无人驾驶的最终目标是实现零人为干预,要求车辆有一定的自我校准能力。开发车辆动力学控制系统旨在提高车辆、用户及周围其他要素的安全性,采用主动控制系统防止由地形、外部因素或驾驶员输入过快而导致的不当行为,控制器性能主要取决于它们对车辆状态和参数的估计程度[1]。车辆动力学控制系统在很大程度上依赖车辆各部分惯性矩、轮胎刚度等参数[2],这些参数随时间变化,无法直接测量,如何得到更准确的车辆行驶状态和参数极为重要。

车辆行驶状态估计方法主要有卡尔曼滤波(Kalman filter,KF)算法[3]及其衍生的各种相关算法,如神经网络[4-5]、状态观测器[6]、模糊逻辑[7]方法等。在简单的线性动力学模型和线性平衡系统中经常采用KF算法,根据系统的输入和输出计算最优估计[8]。输出数据受外界噪声干扰,在某些情况下可把系统的估计过程看作是滤波过程。KF算法主要用于线性高斯系统,当车辆表现出复杂非线性时的估计精度较低[9]。标准扩展卡尔曼滤波(extended Kalman filter,EKF)算法以线性最小方差估计为依据,通过递推算法对状态变量进行滤波估计,是车辆状态估计领域的经典方法,应用广泛[10-11],若系统具有高非线性度时,EKF算法很容易在初始系统的一阶线性分析中产生严重的线性误差,且很难计算出所需的雅可比矩阵,同时该算法为无限增长的记忆滤波器,计算效率和估计精度会随时间的推移而降低。文献[12]提出了一种基于限定记忆随机加权扩展卡尔曼滤波(limited memory random weighted extended Kalman flter,LMRWEKF)算法,响应速度较快,估计精度较高。

无迹卡尔曼滤波(unscented Kalman filter,UKF)算法未采用KF和EKF的方法,即将系统的非线性函数线性化,而是在卡尔曼估计结构中通过无迹变换(unscented transform,UT)方法,调整均值和方差的连续方程进行预测[13-14]。UKF算法无需运算雅可比矩阵,也无需忽略函数中的高阶元素,减小了估计误差,具有测量非线性分布的高精度计算能力[15]。文献[16]在UKF算法中加入遗忘因子进行车辆参数估计,提高了算法对噪声的抑制能力。文献[17]提出一种改进的迭代无迹卡尔曼滤波(improved iterated unscented Kalman filter,IIUKF)算法,在系统方程处于非常严重的非线性状态时,该算法具有较高的估计精度。文献[18]提出了一种基于蚁群优化算法的UKF状态估计自适应滤波算法,运用蚁群算法的寻优能力,提高了算法的鲁棒性和估计精度。

本文基于车辆三自由度动力学模型,分别采用UKF算法、双重无迹卡尔曼滤波算法(dual unscented Kalman filter,DUKF)和采用奇异值分解的改进双重无迹卡尔曼滤波算法(singular value decomposition-dual unscented Kalman filter,SVD-DUKF)估计车辆行驶状态及车辆参数,评估3种算法在车辆一定行驶工况下的状态及参数估计能力。

1 车辆三自由度动力学模型

1.1 车辆模型

只考虑各轮胎的平面运动,忽略滚动和俯仰运动,建立包含纵向、侧向、横摆的车辆三自由度动力学非线性灰箱模型,如图1所示。

a—质心到前轴的距离;b—质心到后轴的距离;Fxfl—左前轮的纵向力;Fxfr—右前轮的纵向力;Fxrl—左后轮的纵向力;Fxrr—右后轮的纵向力;Fyfl—左前轮的侧向力;Fyfr—右前轮的侧向力;δ—前轮转角;ωr—横摆角速度,vx—质心处的纵向速度;vy—质心处的侧向速度。

不考虑空气阻力,车辆三自由度动力学模型方程包括纵向、侧向和横摆方向的动力学方程。纵向的动力学方程为:

侧向的动力学方程为:

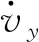
横摆方向的动力学方程为:

1.2 轮胎模型

轮胎支承车辆自重传递驱动和制动力矩,轮胎模型直接影响整车动力学模型的仿真结果[19]。轮胎模型为:

Fxf=Cxsf,Fxr=Cxsr,Fyf=Cyαf,Fyr=Cyαr,

式中:Fxf、Fxr分别为前轴轮胎、后轴轮胎的纵向力;Fyf、Fyr分别为前轴轮胎、后轴轮胎的侧向力;Cx、Cy分别为轮胎的纵向、侧向刚度,设轮胎的刚度相同;sf、sr分别为前轴轮胎、后轴轮胎的滑移率;αf、αr分别为前轴轮胎、后轴轮胎的滑移角,其中αf=δ-arctan[(vy+aωr)/vx],αr=-arctan[(vy-bωr)/vx]。

2 车辆状态估计算法

2.1 UKF算法

UKF算法在卡尔曼估计结构中通过UT变换调整均值和方差的连续方程进行估计,估计精度较高,在强非线性系统中具有一定的鲁棒性。

(1)

式中:Z(t)为考虑噪声的系统观测矩阵,f(·)为非线性状态方程函数,h(·)为非线性观测方程函数,W(t)为系统估计过程中的高斯白噪声,V(t)为系统测量高斯白噪声。

UKF算法通过UT变换得到X(t)的统计特征,即选取2n+1个采样点,公式为:

(2)

式中:X(i)为第i个采样点;P为x的协方差矩阵;λ为缩放比例系数,λ=d2(n+κ)-n,其中d为系数,d的选取控制采样点的分布状态,κ为待选参数,其取值没有界限,但通常应确保矩阵(n+λ)P为半正定矩阵。

计算采样点的权值,公式为:

(3)

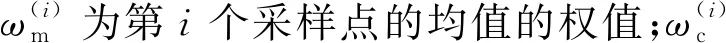
UKF算法基本步骤有以下8步。

1)根据式(2)获取1组采样点(即Sigma点集)

2)计算Sigma点集的一步预测

X(i)(t+1|t)=f[t,X(i)(t|t)]。

(4)

(5)

式中Q为系统过程噪声协方差矩阵。

4)对式(5)再次进行UT变换,产生新的Sigma点集

(6)

5)将式(6)代入式(1),得到预测的系统观测量

Z(i)(t+1|t)=h(X(i)(t+1|t))。

(7)

式中R为测量噪声协方差矩阵。

7)计算卡尔曼增益矩阵K(t+1)=PxtztPztzt-1。

2.2 DUKF算法

图2 DUKF算法运行框架

2.3 SVD-DUKF算法

车辆动力学系统的非线性程度较高时,UKF算法的估计精度下降甚至发散。分析UKF算法的运行过程可知,UT变换过程中,生成Sigma点集时使用Cholesky分解运算误差协方差矩阵,需保证其是非负定矩阵,但在车辆运行过程中,系统协方差矩阵易受噪声影响,导致其成为奇异矩阵而无法处理,从而结束滤波过程,使滤波结果精度下降甚至发散。本文在UT变换中引入奇异值分解(singular value decomposition, SVD)替代Cholesky分解,使算法具有更强的鲁棒性。

SVD算法在机器学习领域应用广泛。假设任意矩阵Am×n的SVD过程可表示为:

Am×n=Um×mΣm×nVn×nT,

式中:U为正交矩阵,即满足UTU=Im×m,且U∈Rm×m;Σ除主对角线外的元素都为0,主对角线上的每个元素称为奇异值;V为正交矩阵,即满足VTV=In×n,且V∈Rn×n。

在UKF算法中采用SVD替代Cholesky分解时,滤波过程的主体过程不变,仅改变产生Sigma点集的过程。对协方差矩阵Pt的SVD过程为:

Pt=UΣVT,

3 仿真结果对比

以MATLAB内置的高刚度轮胎模拟数据为仿真输入数据,前轮的滑移输入为具有恒定偏移的正弦曲线,ωr输入也是正弦曲线,但振幅和频率与滑移输入不同。采用UKF算法估计车辆状态时,因无法估计车辆参数,视正确参数为已知进行仿真。运行仿真时,设每秒迭代10次,仿真结果见图3,误差见图4。

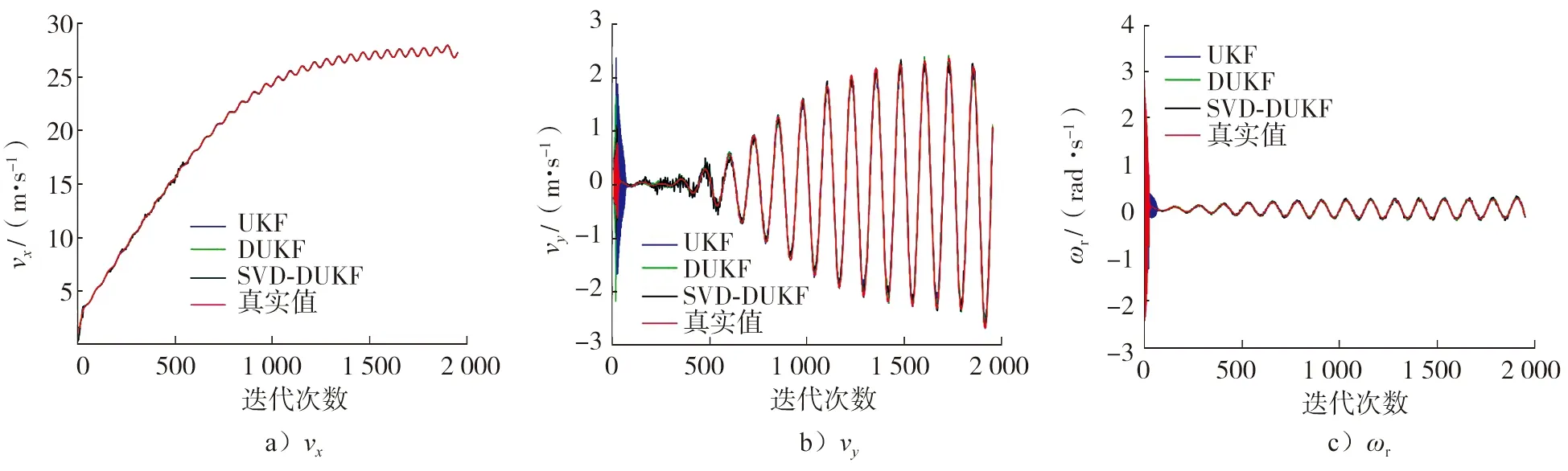
图3 不同算法下车辆状态估计结果

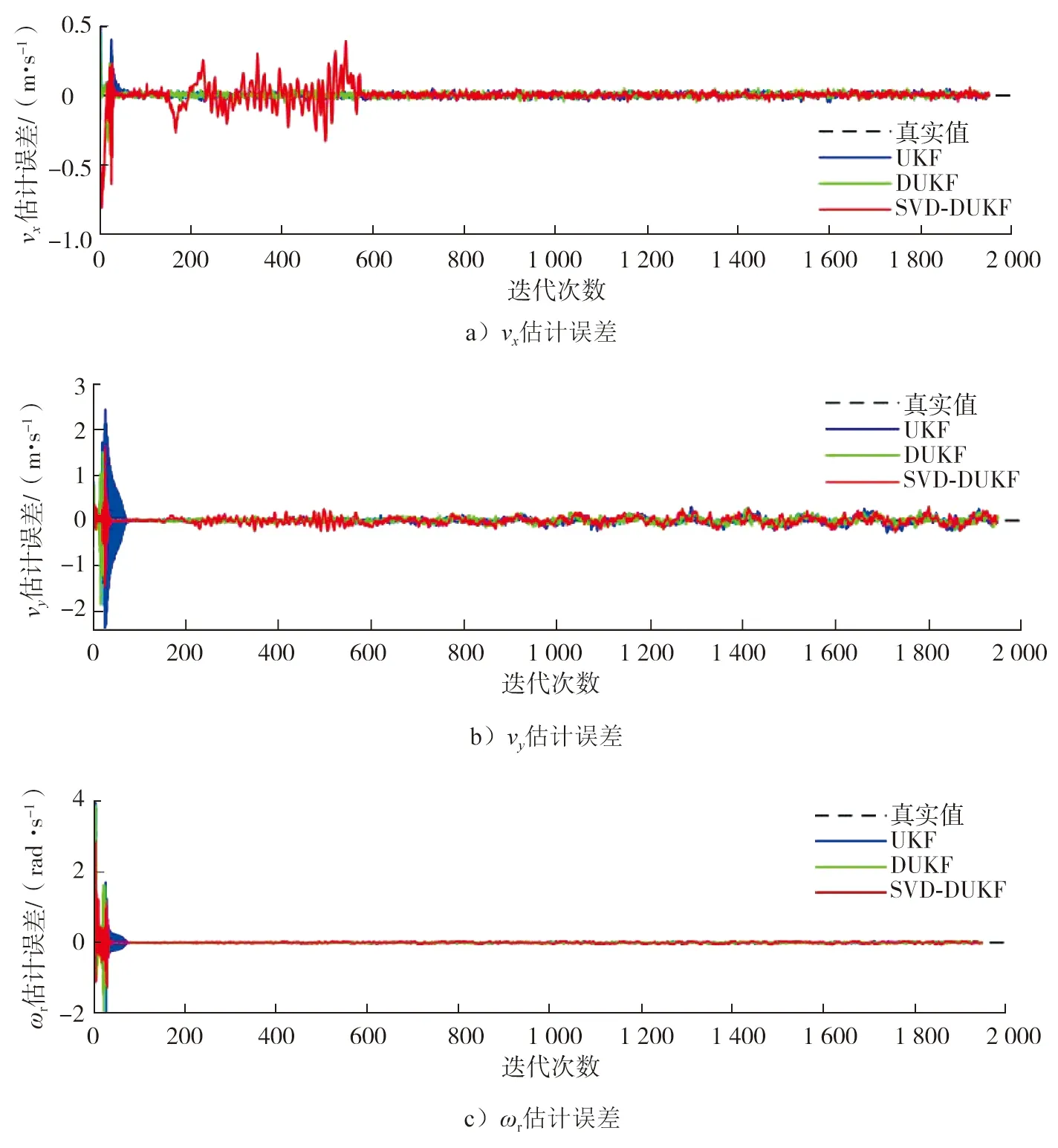
图4 不同算法下车辆状态估计误差

为进一步分析仿真结果,用均方根误差衡量不同算法的估计性能,均方根误差

(8)

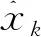
根据式(8),得到不同算法下车辆状态估计的ERMS,如表1所示。由图3、4及表1可知:3种算法的估计结果均较好,但UKF算法中将m等参数列为已知项,与实际情况不符;DUKF算法可同时估计车辆的状态和车辆参数,但在UT变换进行Cholesky分解时,要求协方差为非负定矩阵,有一定限制;SVD-DUKF算法的鲁棒性更强,更适合汽车强非线性系统。

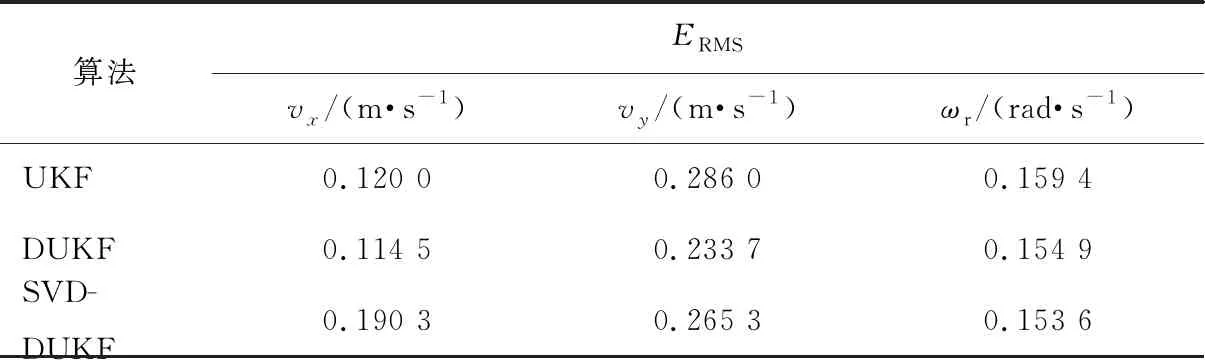
表1 不同算法下车辆状态估计的ERMS

在该车辆动力学模型中,已知m=1 700 kg,Cx=1.5×105N/rad,Cy=5.0×104N/rad。DUKF算法和SVD-DUKF算法对车辆参数估计结果如图5所示。由图5可知:估计m和Cy时,DUKF算法的波动较小,SVD-DUKF算法的误差随仿真进程逐渐减小,最后与DUKF算法均收敛至真实值附近;估计Cx时,SVD-DUKF算法能较快地收敛至真实值并在附近波动,SVD-DUKF算法比DUKF算法的适用性更高。

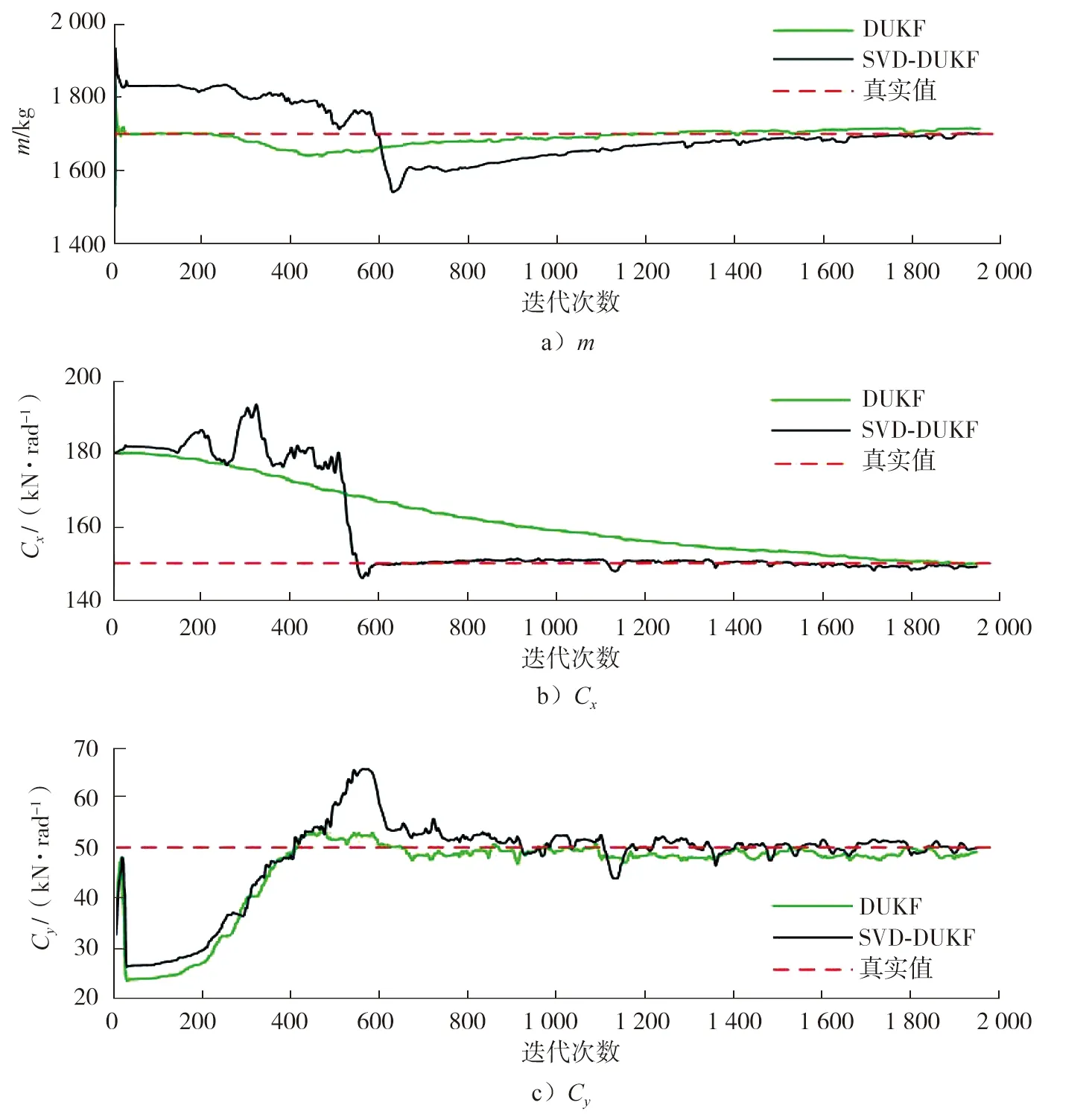
图5 不同算法下车辆参数估计结果

4 结论

基于车辆三自由度动力学模型,分别采用UKF、DUKF、SVD-DUKF 3种算法估计车辆运行状态及车辆参数,在同一工况下采用MATLAB仿真进行比较分析。UKF算法估计车辆状态时需输入车身质量等参数,且随乘客及货物的改变,在车辆实际行驶过程中很难获取正确参数,难以单独在实车中应用算法;DUKF算法通过UT变换获取Sigma采样点集时需进行Cholesky分解,此时需保证协方差为非负定矩阵,否则会导致估计结果不准确甚至发散;通过引入奇异值分解改进DUKF算法,在保证估计精度的同时,算法的适用范围更广,鲁棒性更强。