基于VISSIM仿真的高速公路交通事故拥堵扩散与消散预测

余雪,高超,张冲,武青青,徐长舜,郭春敏

山东交通学院交通与物流工程学院,山东 济南 250357

0 引言

高速公路交通拥堵分为常发性拥堵和偶发性拥堵[1-2]。交通事故造成的拥堵属于偶发性拥堵,对道路通行效率影响较大,准确地预测交通拥堵的影响范围和持续时间,对提高高速公路交通事故救援效率有重要意义。

张辉[3]从高速公路交通拥堵产生及消散过程寻找规律,建立拥堵动态扩散预测模型预测交通流变化。刘红军[4]根据交通流理论,研究区域路网的时空特征,采用K-Means聚类算法划分区域路段速度参数,以交通波模型和Van Aerde模型为基础,从宏观角度寻找交通拥堵扩散规律,构建路网交通拥堵扩散模型。刘格格等[5]采用AnyLogic模型,根据现实情形建立以速度和车头间距为指标的交通拥堵状态评价模型,并验证模型的准确性。袁绍欣[6]从宏观交通流角度出发,采用时间离散化方法建立模型研究交通拥堵,在分析交叉口时,选择通行能力分配离散模型,研究进口道与出口道的拥堵扩散情况。Greenshields[7]基于照片数据采用单一结构线性模型表征交通流的速度与密度间的关系。杨思琪[8]分析异常事件下不同因素对交通拥堵扩散与消散的影响,采用仿真软件VISSIM模拟事故拥堵过程,根据非线性回归分析仿真结果,构建交通事故时空影响预测模型。相关研究多基于宏观角度探索交通拥堵扩散与消散,构建的模型不一定贴合实际情况。主要采用交通流理论中的交通波理论和交通仿真2种方法分析交通拥堵与扩散[9-11],通过交通流理论建立交通拥堵模型,需论证模型是否符合交通流特点,模型的预测精度也需进一步提升。

本文根据交通流三参数理论[12-15],采用软件VISSIM模拟交通事故场景,获取交通流数据,构建高速公路交通拥堵扩散与消散预测模型,计算不同上游到达流量和不同事故车辆阻断时间的高速公路交通拥堵持续时间,并采用VISSIM进行仿真,验证模型的准确性。

1 交通流三参数理论

1.1 传统交通流三参数模型

流量、速度和密度是表示交通流特征的3个参数。美国专家格林希尔兹提出了交通流速度-密度的单段式线性关系模型(格林希尔兹模型)[16],公式为:

v=vf(1-k/kj),

式中:v为交通流速度,km/h;vf为自由流速度,km/h;k为交通流密度,辆/km;kj为阻塞密度,辆/km。

高速公路上车辆逐渐增多(k增大),v会逐渐减小,v与k为线性关系,格林希尔兹模型在交通密度适中的情况下比较符合实际。但格林希尔兹模型与现实交通流数据存在一定偏差,相关学者根据不同的研究方法得到适用于不同交通流状态的关系模型,如格林伯模型、安德伍德模型。格林伯模型适用于交通拥堵状态的交通流,为对数关系模型[16],公式为:

v=vmln(kj/k),

式中:vm为流量最大时的车速,称为最佳车速,km/h。

安德伍德模型适用于交通密度较小的交通流,为指数模型[17],公式为:

v=vfe-k/km,

式中:km为流量最大时对应的交通流密度,称为最佳密度,辆/km。

交通事故阻断具有突发性和高密度拥堵的特点,存在由低密度向高密度的跃迁,采集高密度和低密度变化的数据较困难。本文采用VISSIM仿真的方法获取交通事故拥堵和不拥堵状态下交通流关系模型。

1.2 基于VISSIM仿真的交通流三参数模型

本文研究双向四车道交通拥堵时流量与密度的关系,采用软件VISSIM模拟交通事故场景。仿真路段为长10 km、限速100 km/h的高速公路,驾驶行为类型选择Wiedemann99模型,设置单侧车道事故,并产生拥堵,输入上游到达流量分别为1 000、2 000、3 000、4 000 辆/h,模拟多种交通流状态。高速公路交通拥堵仿真示意图如图1所示。

图1 高速公路交通拥堵仿真示意图

在软件VISSIM中设置预热时间为1 000 s,剔除预热前的不稳定数据,确保流量完全加载。在高速公路右侧道路设置事故车辆拥堵点,在拥堵点上游、下游和拥堵区域每隔100 m设置数据检测器,阻断时间为1 h,得到不同上游到达流量下,下游交通流率的变化如图2所示。由图2可知:上游到达流量小于2 000 辆/h时,高速公路单车道通行能力大于上游到达流量,因此单车道阻断不会发生交通拥堵;上游到达流量大于2 000 辆/h时,上游到达流量超过高速公路单车道通行能力,在阻断时间内,车流通行流量受限,车流随机波动现象被抑制,表现为以某一稳定流量通过拥堵路段。上游到达流量越大,拥堵持续时间越长,拥堵时间与上游到达流量正相关。

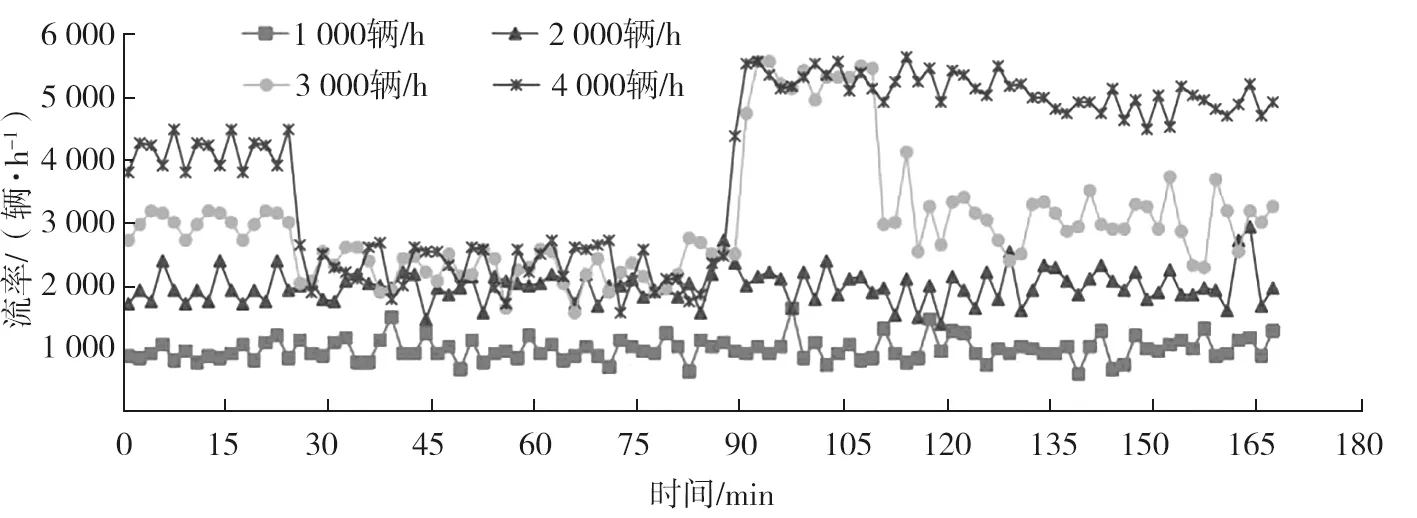
图2 不同上游到达流量下下游交通流率的变化

以15 min为间隔统计交通拥堵路段的交通流数据,通过数据拟合得到拥堵和不拥堵2种状态下交通流速度-密度拟合散点图,如图3所示。由图3可知:不拥堵状态到拥堵状态为跃迁变化,不符合格林希尔兹模型,不拥堵状态和拥堵状态下速度与密度的关系模型表现为分段模型。通过拟合分别得到不拥堵、拥堵状态的速度与密度间的关系式为:

图3 交通流速度-密度拟合散点图

(1)

式中:v1、v2分别为不拥堵、拥堵状态的交通流速度;vf1、vf2分别为不拥堵、拥堵状态的自由流速度;k1、k2分别为不拥堵、拥堵状态的交通流密度;kj1、kj2分别为不拥堵、拥堵状态的阻塞密度。

令a1=vf1/kj1,b1=vf1,a2=vf2/kj2,b2=vf2,对图3中的散点数据进行拟合,得到相关参数为:a1=-0.06,b1=91.68,R12=0.81,a2=-0.36,b2=53.63,R22=0.95。高速公路交通流数据在拥堵状态和不拥堵状态的拟合效果较好,说明所建立的分段模型能较好地描述不拥堵状态和拥堵状态的交通流。

2 交通拥堵扩散与消散预测模型

2.1 交通拥堵扩散过程建模

根据高速公路交通事故区域上、下游交通状态,将高速公路划分为上游车辆到达区域、中游交通拥堵区域和下游事故影响恢复区域[18-20]。上游车辆到达区域和中游交通拥堵区域交界处形成集结波,根据格林希尔兹模型及交通波理论,结合式(1),推导得到集结波的波速

vw1=(Q1-Q2)/(k1-k2),

式中:Q1为不拥堵路段的流量,Q1=vf1(k1-k12/kj1);Q2为拥堵路段的流量,Q2=vf2(k2-k22/kj2)。

2.2 交通拥堵消散过程建模

清除交通事故车辆后,在中游交通拥堵区域和下游事故影响恢复区域交界处形成消散波,下游车辆以最大流量疏散,根据交通波理论,得到消散波的波速

vw2=(Q2-Q3)/(k2-k3),

式中:Q3为清除事故车辆后的流量,Q3=vf1(k3-k32/kj1);k3为清除事故车辆后的密度。

2.3 交通拥堵持续时间建模

清除交通事故车辆后,在中游交通拥堵区域和下游事故影响恢复区域交界处形成消散波的同时,上游车辆到达区域和中游交通拥堵区域交界处的集结波仍存在。简化集结波波速和消散波波速公式,得到:

vw1=(vf1k1-vf2k2-vf1k12/kj1+vf2k22/kj2)/(k1-k2),

(2)

vw2=(vf2k2-vf1k3-vf2k22/kj2+vf1k32/kj1)/(k2-k3)。

(3)

设从事故发生到清除事故车辆的时间为t0,清除事故车辆到完成交通拥堵消散的时间为ts,交通拥堵持续时间为tj,则|vw1|(t0+ts)=|vw2|ts,ts=|vw1|t0/(|vw2|-|vw1|),tj=t0+ts=|vw2|t0/(|vw2|-|vw1|)。

3 仿真验证

采用软件VISSIM模拟交通事故造成的单车道阻塞,上游到达流量分别为2 000、2 500、3 000、3 500、4 000 辆/h,预热1 000 s,t0分别为60、90、120、150、180 min。

根据式(2)(3)计算不同上游到达流量下的vw1与vw2,如表1所示。分别采用高速公路交通拥堵扩散和消散预测模型、VISSIM仿真得到不同上游到达流量和不同t0时的计算结果tj与仿真结果tj′,见表2。

表1 不同上游到达流量下的波速

表2 不同上游到达流量和不同t0下的tj与tj′

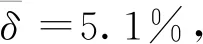
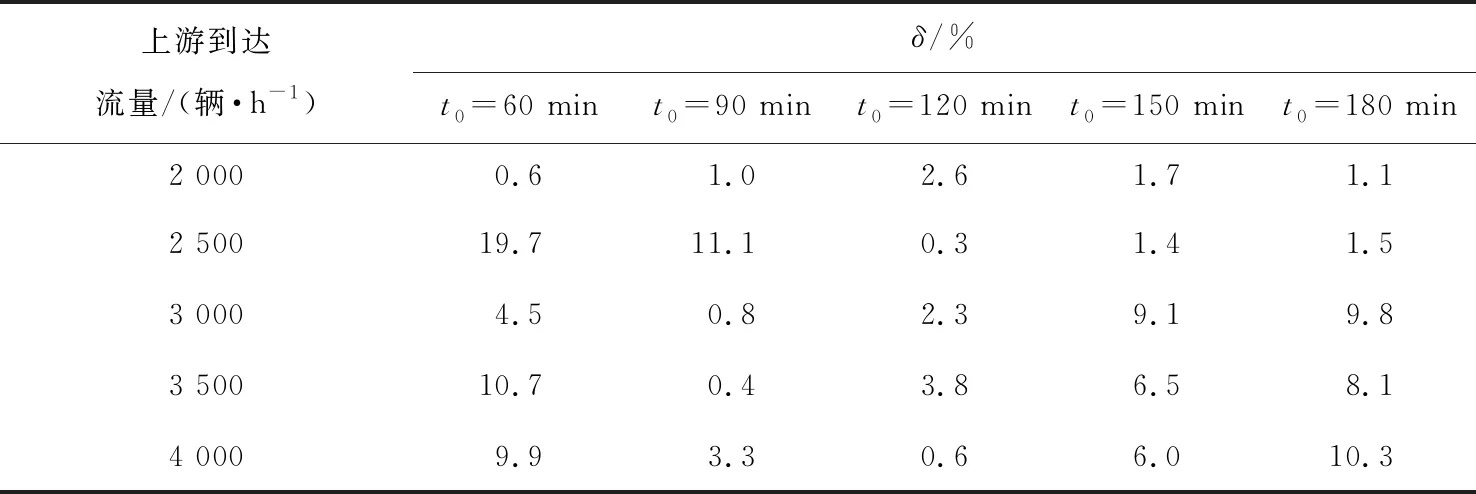
表3 不同上游到达流量和不同t0下tj与tj′的δ

4 结论

本文基于交通流三参数理论和交通波理论,分析高速公路交通事故拥堵演变过程,采用软件VISSIM仿真获取交通事故拥堵和不拥堵状态下的交通流数据,建立高速公路交通拥堵扩散和消散预测模型。

1)交通事故阻断具有突发性和高密度拥堵的特点,存在由低密度向高密度的跃迁,交通流三参数关系不再符合格林希尔兹模型,在拥堵和不拥堵情况下速度与密度的关系模型表现为分段模型。

2)建立基于分段交通流三参数模型和交通波理论的高速公路交通拥堵扩散与消散预测模型,通过仿真验证,该模型预测准确度约为95%,可较好地预测高速公路交通拥堵持续时间。

3)交通拥堵的影响程度与上游到达流量、事故车辆阻断时间等因素有关,上游到达流量越大、事故车辆阻断时间越长,交通拥堵持续时间越长。

高速公路交通拥堵扩散和消散预测模型对科学合理地安排交通事故的救援工作,尽快疏导交通拥堵,减少道路交通损失具有重要意义。