高中生数学建模素养测评模型的构建

杨正朝 熊星月 卢信羽 杨正朝

【摘 要】  数学建模是高中数学核心素养之一，是对现实问题进行数学抽象、用数学语言表达问题、用数学方法构建模型解决问题的素养.研究基于已有测评模型的研究思路，构建了以3个一级指标（问题意识、构建模型、模型应用）和9个二级指标组成的高中生数学建模素养测评模型.通过专家咨询法，进行指标修正和完善，结合测评指标体系编制调查问卷，结果显示调查对象对已构建的指标体系总体认同度较高，信效度较好，并利用因子分析法，得出其测评模型的线性表达式：X=0.32A+0.35B+0.33C.

【关键词】  数学核心素养；高中生；数学建模；测评指标；测评模型

1   问题提出

在传统数学教学中，对于数据分析、数学运算、逻辑推理等数学核心素养，往往能够在一线高中教学中看到其身影，但是数学建模素养很少在教学中得以体现，很多学校甚至很少涉猎.大多數教师认为数学建模在高考试题中占比少、涉及的知识点较为抽象、学习难度大、过于专业化等，纷纷对此望而却步，没有引起重视，认为数学建模应该是小众化培养，很少有教师刻意去开展数学建模教学，这就导致了其离课堂渐行渐远.随着《普通高中数学课程标准（2017年版）》（以下简称《课标（2017年版）》）提出将数学建模作为高中六大数学核心素养之一［1］，足以见得数学建模素养在人才培养中的重要性，是学生必备的关键能力，是学生适应社会发展的需要.课标颁布以后，关于数学建模素养的研究也逐渐增多，却很少看到一个操作性较好的高中生数学建模素养测评指标评价体系，尽管课标有划定出数学建模素养的水平，但是介于其操作难度大，让一线数学教师无从下手.同样地，从社会层面来看，随着社会的发展和进步，现实问题愈加凸显，如何从复杂的现实情境中，选取相关内容构建数学模型，以解决实际问题就显得尤为关键.测评模型作为教育发展和人的素养发展评估的重要检测工具，也是一项实证研究.但由于国内对数学核心素养的研究起步晚，测量与评价研究体系不够成熟［2］.

在发展学科核心素养为导向的基础教育阶段，评价是落实核心素养的前提和基础.对数学建模素养进行测评模型探索，具有一定的代表性，能够为相关研究提供参考. 2   文献综述 2.1 数学建模素养测评的研究

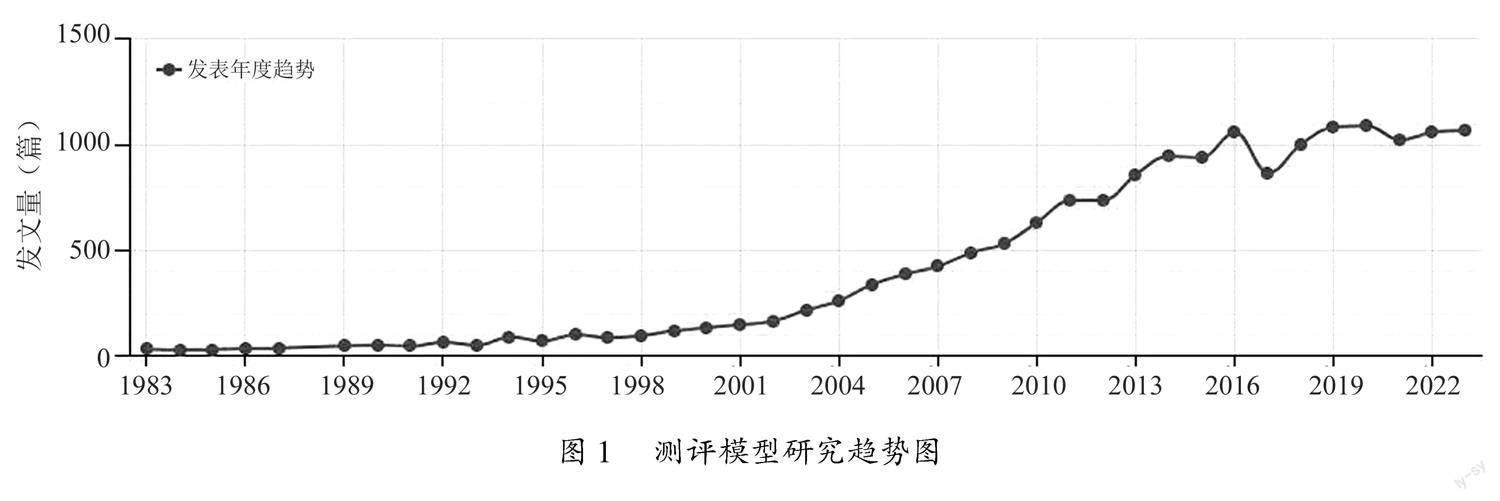
祖丹等基于数学建模的过程性特征，从纵横的角度构建了以模型假设、模型构建、模型检验为主的数学建模能力测评框架，并划分了具体水平梯度，该框架的专家咨询和测验结果均收获了较高的信效度［3］.李贺、张卫明利用数学质量检测试题，统计了与数学建模相关的试题，并分析其得分和水平层次，以了解初中生数学建模发展现状［4］.张瀚兮结合专家咨询法， 得到高中生数学建模素养测评指标，其由5个一级指标和17个二级指标构成，一级指标分别是：数学化、建立数学模型、求解数学问题、数学表达、处理数学结果，再利用层次分析法求出各指标权重值，最后予以验证［5］.朱娅梅针对义务教育阶段的学生，将数学建模能力由低到高划分为三个水平：再现、联系和反思，而且提出了各行为测评指标［6］.田芳将数学建模素养的行为表现划分为四个维度，即发现和提出问题、建立和求解模型、检验和完善模型、分析和解决问题，并将每个维度分为3个水平，结合测试卷和调查问卷对高中生进行施测，以了解学生的数学建模现状，以此提出：注重阅读理解，提高转化能力；注重建模结果，体会建模过程；重视模型思想，提高建模能力；立足高考，提高数学建模的重要性等数学建模培养策略［7］.孙凯结合初中生认知心理特征，从问题情境、数学内容、建模过程、任务类型、建模水平五个方面构建初中生数学建模能力测评框架，并对应的提出测试题案例［8］. 由上可知，数学建模的研究更多地涉及内涵、培养策略、试题分析及评价等方面，尽管有包含数学建模测评模型的研究，但是相对较少.2.2 数学核心素养的测评研究目前，数学教育界对于数学核心素养测评的研究主要涉及以下4个领域：一是数学核心素养的试题测评，如杨正朝等利用喻平的测评框架对2022年高考试题进行研究［9］.二是数学核心素养的评价框架，如喻平从知识学习的角度出发，将数学核心素养评价框架划分为知识理解、知识迁移、知识创新［10］；朱立明以数学知识、问题解决、数学思维构建的数学核心素养评价框架［11］.三是数学核心素养的测评模型，如陈蓓先是自编咨询表，然后通过Yaahp层次分析，构建了由6个一级指标14个二级指标组成的数学核心素养测评模型，并以此模型为基础，编制高中生数学核心素养测试卷，用于检测模型的普适性［12］.颜飞利用专家咨询法构建了由6个一级指标和18个二级指标组成的高中生数学核心素养评价体系，接着利用层次分析法计算各指标权重，最后借助模糊综合评判法和实际测试对测评模型进行验证［13］.四是数学素养操作定义.如王光明将数学内容、现实情境、数学过程等作为高中生数学素养的操作定义［14］.可见，近年来对于数学核心素养的研究面越来较广，这既为数学建模素养测评模型研究思路的形成，提供了一定的研究范式，也为后期丰富数学建模素养的发展，起到了推动作用.2.3 关于测评模型的研究通过中国知网，在检索主题中输入“测评模型”，截止至2023年4月19日，统计到测评模型相关论文发表趋势图，如图1所示.由图可知，近年来关于测评模型的研究相比以往有一定的增势，反映了该研究的热度较高.

在数学教育领域，关于测评模型的研究也在如火如荼地开展.例如小学生几何直观能力测评模型［15］、高中生数学推理能力测评模型［16］、高中生数学直观想象素养测评模型［17］、高中生数学学科核心素养测评指标体系［18］等.不难发现，尽管研究的主题不一样，但是研究的思路大同小异，尤其是测评模型方面的研究都是基于专家咨询法、因子分析法、层次分析法等，采用定性和定量相结合的方法进行测评模型构建，这对数学建模素养测评模型的构建具有重要的借鉴意义. 3   高中生数学建模素养测评指标体系的构建

3.1 高中生数学建模素养测评指标的初步构建《课标（2017年版）》指出数学建模的主要表现是：发现和提出问题、建立和求解模型、检验和完善模型、分析和解决问题［1］.根据课标和现有研究成果，初步构建了数学建模素养测评指标，如表1所示.

3.2 专家对测评指标的修正和完善 为了使数学建模素养的测评指标更为科学、合理，研究基于专家咨询法编制专家咨询问卷，以问卷星的方式发放给10位数学教育领域的专家，邀请其对上述测评指标提出相应的意见和建议.经过两轮专家咨询，专家对测评指标总体较为认可，但是也存在一些指标划分的问题：一是将一级指标“模型意识”改为“问题意识”，主要原因在于数学建模素养更多是以数学问题为出发点，结合课标可知，数学建模初始阶段为发现和提出问题，应该强调问题提出在数学建模研究中的重要性.二是将二级指标“对数学问题进行计算”改为“建立模型的表征信息”，数学建模不单单包含计算，还涉及图表信息、幾何、公理、表达式等问题，可将其归纳为“建立模型的表征信息”过程.

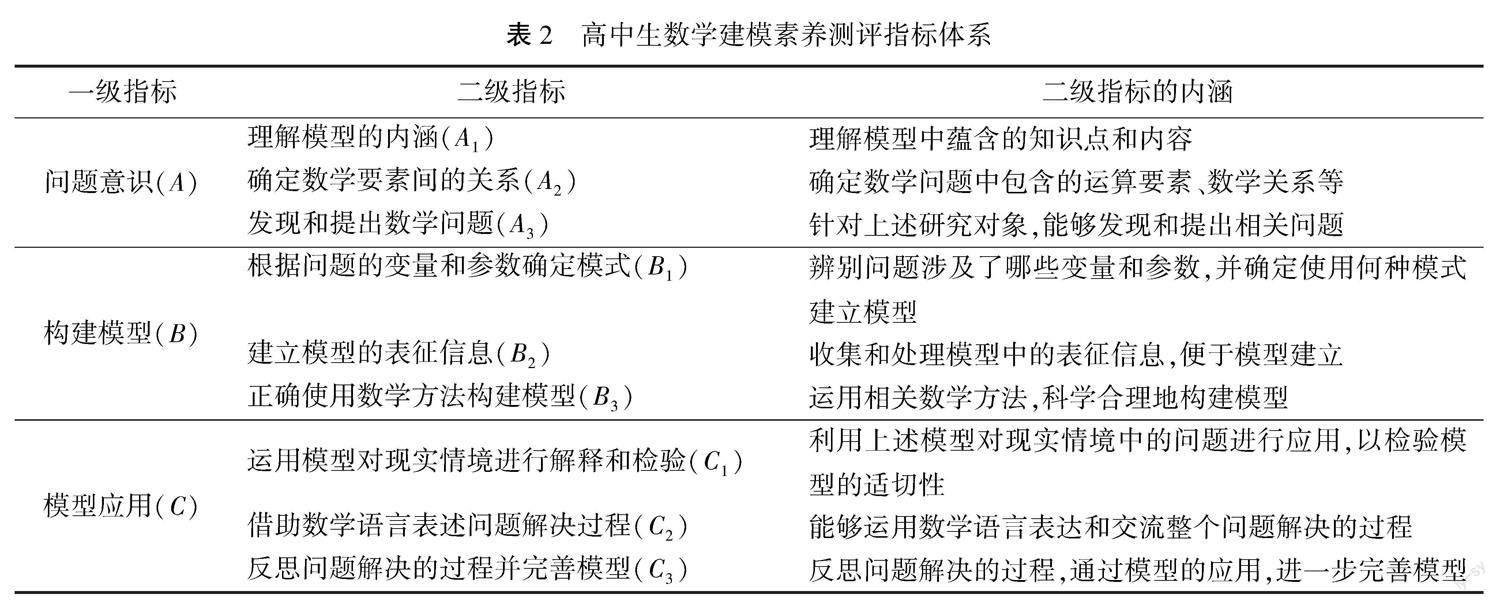
3.3 高中生数学建模素养测评指标体系的确立

通过上述专家对指标的修订和完善，最终得到高中生数学建模素养测评指标体系，见表2.

4  高中生数学建模素养测评指标认同度的分析

为了验证上述测评指标体系的合理性，研究采用李克特五点评分法进行问卷设计，以问卷星的形式，向数学教育专家、中学数学教师等160名调查对象发放问卷，最终收回问卷156份，回收率97.5%.4.1 测评指标的总体认同度分析

通过统计各指标分数的平均值情况，绘制条形图，如图2所示.其中，一级指标中的问题意识、构建模型认同度较高，

二级指标中确定数学要素间的关系、发现和提出数学问题、正确使用数学方法构建模 型认同度较高.总体来看，各调查对象对上述测评指标体系认同度较高，均在4.00以上.

4.2 调查问卷的信效度分析

针对上述问卷数据，利用SPSS26.0进行信度分析，其结果为0.961，显示了较高的信度.再对其进行效度分析，一方面，调查问卷是围绕测评指标体系而设计，因此保证了良好的内容效度；另一方面，用SPSS26.0进行分析，其KMO值为0.945，表明该问卷具有较高的效度.4.3 一阶验证性因子分析

研究提出的测评指标能否正确表达高中生数学建模素养，需要实际检验考证.其主要从测评指标与实际调查数据的适配性来体现.下面对调查问卷数据进行一阶验证性因子分析，以了解一级指标与二级指标之间的关系.利用AMOS26.0进行分析，拟合优度指标如表3，其中χ2/df值在1～3之间，P小于0.001，GFI，NFI，RFI，IFI，CFI等均大于0.9，RMSEA=0.063<0.08，SRMR=0.025<0.08，表明模型适配度较好.

进一步开展一阶验证性因子分析（见图3），图中3个一级指标和9个二级指标的因子载荷量都大于0.6，表明适配度良好.

5  高中生数学建模素养测评模型的构建

在一阶验证性因子分析中，三个潜在变量（一级指标）因子载荷量分别为0.90，0.92，0.84（大于0.6），说明三个潜在变量还能够被另一个潜在变量 （称为“高中生数学建模素养”）解释，利用调查问卷数据，继续进行二阶验证性因子分析（见图4），适配指标值和一阶验证性因子一样，这里不再赘述.

通过上述二阶验证性因子分析，研究基于高中生数学建模素养测评模型的假设，利用二阶标准化计算权重值，结果见表4.

利用表格中归一化后数值，将其用线性方程表示出来，得到高中生数学建模素养测评指标模型：

X=0.32A+0.35B+0.33C，其中，A=0.35A1+0.35A2+0.30A3，

B=0.34B1+0.32B2+0.34B3，C=0.33C1+0.34C2+0.33C3.

6   结论及反思

研究借鉴相关测评模型研究思路，利用专家咨询法，修订和完善测评指标.结合测评指标体系编制调查问卷，结果表明专家认同度总体较高.借助因子分析法，检测结果显示其测评指标适配性较好，能够很好地体现高中生数学建模素养，最终得到高中生数学建模素养测评模型：X=0.32A+0.35B+0.33C，其中A表示问题意识，B表示构建模型，C表示模型应用.

对于上述研究，提出几点反思：一是三个一级指标中，构建模型权重值较大，一方面反映了相关专家较为看重构建模型的过程，另一方面也体现了这一过程对于学生而言难度较大，需要学生具备一定的知识储备和方法积累.二是模型应用是学生学以致用能力的体现，学生能否正确应用模型分析和解决实际问题，是数学建模的根本体现，是适应社会发展的需求.三是由于时间和条件限制，无法根据上述测评模型编制测试卷，模型的适切性有待今后进一步探究.

参考文献

［1］  中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］  杨正朝，熊星月，唐四雨.基于CiteSpace可视化分析下的数学核心素养研究现状及启示［J］.中学数学杂志，2022（05）：1-5.

［3］  祖丹，丁锐，孔凡哲.双维多水平数学建模能力测评框架的构建［J］.数学教育学报，2022，31（04）：56-61.

［4］  李贺，张卫明.基于质量检测的初中学生数学建模发展状况的调查研究［J］.数学教育学报，2017，26（01）：19-21.

［5］  张瀚兮. 高中生数学建模素养测评指标体系构建研究［D］.重庆：西南大学，2019.

［6］  朱婭梅.义务教育阶段学生数学建模能力评价框架和行为测评指标［J］.数学教育学报，2018，27（03）：93-96.

［7］  田芳. 普通高中学生数学建模素养养成策略研究［D］.兰州：西北师范大学，2019.

［8］  孙凯.初中生数学建模能力评价框架的构建［J］.内蒙古师范大学学报（教育科学版），2023，36（01）：83-88.

［9］  杨正朝，吴京霖，王宽明.核心素养视域下高考数学试卷评析——以2022年高考数学四套试卷为研究对象［J］.教学月刊·中学版（教学参考），2023（Z1）：109-115.

［10］  喻平.数学核心素养评价的一个框架［J］.数学教育学报，2017，26（02）：19-23.

［11］  朱立明.高中生数学学科核心素养测评与课程标准一致性研究［J］.教育科学研究，2022（02）：92-96.

［12］  陈蓓. 高中生数学核心素养评价研究［D］.南京：南京师范大学，2017.

［13］  颜飞. 高中生数学学科核心素养测评指标体系研究［D］.兰州：西北师范大学，2021.

［14］  王光明，张楠，周九诗.高中生数学素养的操作定义［J］.课程·教材·教法，2016，36（07）：50-55.

［15］  张和平，裴昌根，宋乃庆.小学生几何直观能力测评模型的构建探究［J］.数学教育学报，2017，26（05）：49-53.

［16］  王宽明. 高中生数学推理能力测评模型的研究［D］.贵阳：贵州师范大学，2021.

［17］  郑雪静，陈清华，柯跃海.高中生数学直观想象素养测评模型的构建［J］.教育研究与实验，2021（03）：71-78.

［18］  朱立明.高中生数学学科核心素养测评指标体系的构建［J］.教育科学，2020，36（04）：29-37.

作者简介  杨正朝（1990—），男，贵州榕江人，硕士研究生;主要从事数学教育研究.

熊星月（1999—），女，贵州毕节人，硕士研究生;主要从事数学教育研究.

卢信羽（1997—），女，贵州纳雍人，硕士研究生;主要从事数学教育研究.