求解逆运动学的多策略蜻蜓算法

黄华娟,闵峰

(广西民族大学 a.人工智能学院;b.电子信息学院,南宁 530006)

最优化是应用数学的一个分支,主要指在一定的条件限制下,选取某种研究方案使目标达到最优的一种方法.最优化问题在当今的军事、工程、管理等领域都有着极其广泛的应用.蜻蜓优化算法(Dragonfly Algorithm,DA)是MIRJALILI［1］于2016年提出的一种新型智能优化算法.其主要灵感源于自然界中蜻蜓的静态和动态群集行为,在解决优化问题时［2］,它存在收敛精度低,容易陷入局部最优解,求解时间长与不稳定等缺点.

针对以上问题,国内外学者做了很多的优化与改进.高旭等［3］提出基于自适应权重的蜻蜓算法,通过自动调整原聚集、壁撞与结对等3种权重,改善算法的勘探能力,并应用于瑞雷波频散曲线反演中.薛海峰等［4］针对风电并网协调输电网扩展规划问题,提出基于离散多目标蜻蜓算法,并对风电协调输电网扩展规划模型进行求解.YUAN等［5］提出了自适应阻力和耐力的蜻蜓算法,用3个著名的约束工程问题验证了其可行性.张颖等［6］对蜻蜓算法的迭代进化机制进行改进,将聚类中心等效为蜻蜓个体编码,利用蜻蜓算法的寻优优势,改善模糊C均值聚类性能.NAGA LAKSHMI等［7］基于混合遗传蜻蜓算法对径向配电系统配电电源进行优化.CHANTAR等［8］通过混合二进制蜻蜓算法,融合模拟退火机制用于特征选择.SALGOTRA等［9］针对算法搜索性差,内聚和对齐不平衡等问题,提出了变异算子的概念,并提出了7个版本的DA,遵循自适应参数、世代划分、改进的开发阶段和线性递减的种群适应来改进DA的搜索、收敛和其他特性.

上述的改进策略能在一定程度上提升蜻蜓算法的迭代寻优能力,但是大多数研究仅对算法的权重进行调整,并没有改善蜻蜓算法易陷入局部解与其优化能力不稳定等缺陷.为此,本文提出了一种多策略改进蜻蜓算法.首先针对算法初始种群的随机性,本文采用Logistic混沌映射初始化种群,使算法能够更快地锁定最优解区域.其次,采用共生生物搜索算法,改善蜻蜓算法的勘探与开发能力,增强寻优过程中的信息交流.最后,采用余弦扰动避免算法过早陷入局部最优解.从算法初始化,到改善算法的勘探和开发能力,再到最终的变异策略,全面优化了蜻蜓算法.为了验证MIDA的性能,本文采用12个基准函数与其他热门的优化算法进行比较,同时应用于逆运动学求解五自由度机械臂的参数中.实验结果表明,MIDA相较于其他算法,在函数优化中有着巨大的优势,同时更加稳定,并且在逆运动学中的表现更加精确与稳定.

1 蜻蜓算法

1.1 基本理论

蜻蜓算法是一种新型的元启发式群智能优化算法,其原理是模拟大自然中蜻蜓寻找猎物的行为.该算法源于自然界中蜻蜓动态和静态的智能群行为,对蜻蜓的飞行路线、躲避天敌及寻找食物等生活习性进行数学建模.在动态群中,为获得更好的生存环境,大量的蜻蜓集群朝着共同的方向进行远距离迁徙;在静态群中,为寻找其他飞行猎物,由小部分蜻蜓组成的各个小组,在较小的范围内来回飞行.蜻蜓飞行过程中的局部运动与飞行路径的临时突变是静态群的主要特征.在自然界中,蜻蜓的生活习性可以归纳为5类行为方式:排队、结盟、分离、寻找猎物和躲避天敌.这5类行为的数学模型如式(1)所示:

(1)

其中,X是当前蜻蜓所在位置,N是邻近蜻蜓的个数,Xj是第j只相邻蜻蜓所处位置,Vj是第j只相邻蜻蜓的飞行速度,X+是待捕食的食物所处的位置,X-是天敌所处位置.

Ai代表第i只蜻蜓排队行为的位置向量;Ci代表第i只蜻蜓结盟行为的位置向量;Si代表第i只蜻蜓分离行为的位置向量;Fi代表第i只蜻蜓猎食行为的位置向量;Ei代表第i只蜻蜓逃避天敌行为的位置向量.

蜻蜓个体飞行步长向量更新公式如下:

ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+ωΔXt,

(2)

其中s代表分离权重;a代表对齐权重;c代表凝聚权重;f代表猎物权重因子;e代表天敌权重因子;ω代表惯性权重;t代表当前迭代次数.蜻蜓个体的位置更新公式如下:

Xt+1=Xt+ΔXt+1,

(3)

其中t是当前迭代次数,Xt是当前个体的位置向量,ΔXt+1是步长向量.

上述迭代公式为蜻蜓个体周围有邻近个体,当某只蜻蜓没有相邻个体时,通过使用Lévy飞行的方法绕搜索空间飞行,在这种情况下,蜻蜓位置根据以下公式进行更新:

Xt+1=Xt+Lévy(d)ΔXt,

(4)

其中t表示当前迭代次数,d代表位置向量的维度.

Lévy飞行的计算公式如下:

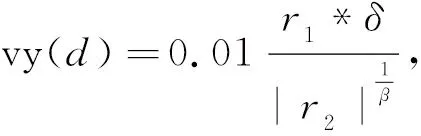
(5)

其中r1,r2是两个［0,1］的随机数,β是一个常数(本文为1.5),δ的计算方法如下:

(6)

其中Γ(x)=(x-1)!

1.2 DA的算法步骤

蜻蜓算法的步骤如下:

步骤1 初始化种群参数,包括种群数量n,最大迭代次数i_max,位置向量X,方向向量ΔX.

步骤2 计算各个个体的适应度值,确定该种群的食物位置与天敌位置.

步骤3 更新权重,包括领域半径r、对齐权重a、分离权重s、凝聚权重c、天敌与猎物权重因子e,f.

步骤4 通过式(1)更新各项位置向量.

步骤5 通过式(2)～(4)更新蜻蜓的位置.

步骤6 判断新的位置解是否更优,选取更优的解位置.

步骤7 重复步骤2到步骤6,直到满足最大迭代次数.

2 多策略改进的蜻蜓算法

为了提高算法的收敛速度、最优解的质量以及稳定性,本文提出一种多策略改进的蜻蜓算法(MIDA),从初始解的选取,勘探与开发过程的改进和余弦扰动3个方面进行改进.

2.1 Logistic混沌映射

混沌是非线性动力系统,描述的是任意随时间变化的过程,这个过程是类似随机的、非周期具有收敛性的,同时初始值对其影响极大.其数学表达式如下:

Xn+1=Xnμ(1-Xn),

(7)

其中,Logistic参数μ∈［0.0,4.0］,研究表明,当x∈［0.0,1.0］时,Logistic映射为混沌状态,即:在此映射作用下产生的序列是非周期的.

图1为Logistic参数μ在［2.6,4.0］区间内,X0为0.5时的Logistic映射图,从图1中可以看出μ值越接近4.0,X的取值越无限分布在［0.0,1.0］区间内.因此本文的μ值取为3.999.

表1呈现的是Logistic的随机分布特性,取X0=0.2,μ=3.999,迭代10 000次的结果.分布情况如表1所示.

表1 映射值的分布范围

由图2与表1可知:Logistic映射的迭代序列分布并不均匀,呈中间小两头大的情形,虽然分布不均,但足以满足需求.

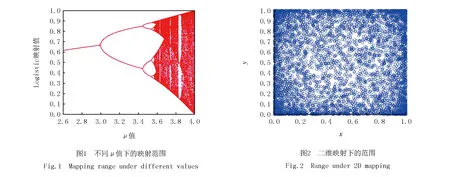
Logistic映射产生的数值在［0.0,1.0)间,本文通过式(8),将范围扩展到解空间中.

Xi=Xi×(Xmax-Xmin)+Xmin.

(8)

2.2 共生生物搜索算法

共生生物搜索算法是一种基于生物学中共生现象的启发式搜索算法,该算法参数少,操作简单、易于实现且稳定性好.其中包括互利与共栖阶段.

在生态系统中,两个生物保持互利关系,其表达式如下:

(9)

式中RMV代表了Xi和Xj的交互关系;rand(0,1)是［0,1］间的随机数;Xbest为最优个体;bf1和bf2为利益因子,其值取为1,表示部分受益.

在共栖阶段,生物Xi与Xj交互,使得Xi受益,Xj不变.其表达式如下:

Xi=Xi+rand(-1,1)(Xbest-Xj),

(10)

其中Xbest-Xj表示Xj对Xi提供的好处,即Xj帮助Xi提高对生态系统的适应度.

因此,MIDA位置更新的表达式如下:

(11)

在前半部分的迭代中采用互利关系,重点在于蜻蜓个体间的信息交互,有利于勘探过程,在迭代的后半段采用共栖方式,有利于局部解的开发.

2.3 余弦扰动

在蜻蜓算法中,每次的更新迭代采用的是贪心策略,即每次选取较优解作为新位置,但是到了迭代后期陷入局部解的情况下,不对其进行改进便会始终为同一解,使得该算法一直在做无用功.

为改善算法的寻优能力,采用余弦扰动的方式对未取得更优解的个体进行变异操作,采取该方式是因为余弦函数因子具有振荡特性,余弦扰动公式如下:

Xi=cos((π×t)/(Max_i))×Φ×Xi,

(12)

其中φ∈［-1,1］的随机数,Max_i是最大迭代次数,Xi是第i代蜻蜓所处位置.

2.4 MIDA的算法流程

根据以上策略,MIDA的伪代码如下.

算法 多策略改进的蜻蜓算法

1.混沌初始化蜻蜓在搜索区域中的位置

2.初始化种群参数,包括种群数量n,最大迭代次数Max_i,方向向量ΔX,通过logistic映射确定位置的向量X

3.while结束条件未满足

4. 计算各个个体的适应度值,确定该种群的食物位置与天敌位置

5. 更新各项权重,包括领域半径r、对齐权重、分离权重、凝聚权重、天敌与猎物权重因子

6. 通过式(1)更新各项位置向量

7. 通过式(9)～(11)更新蜻蜓的位置

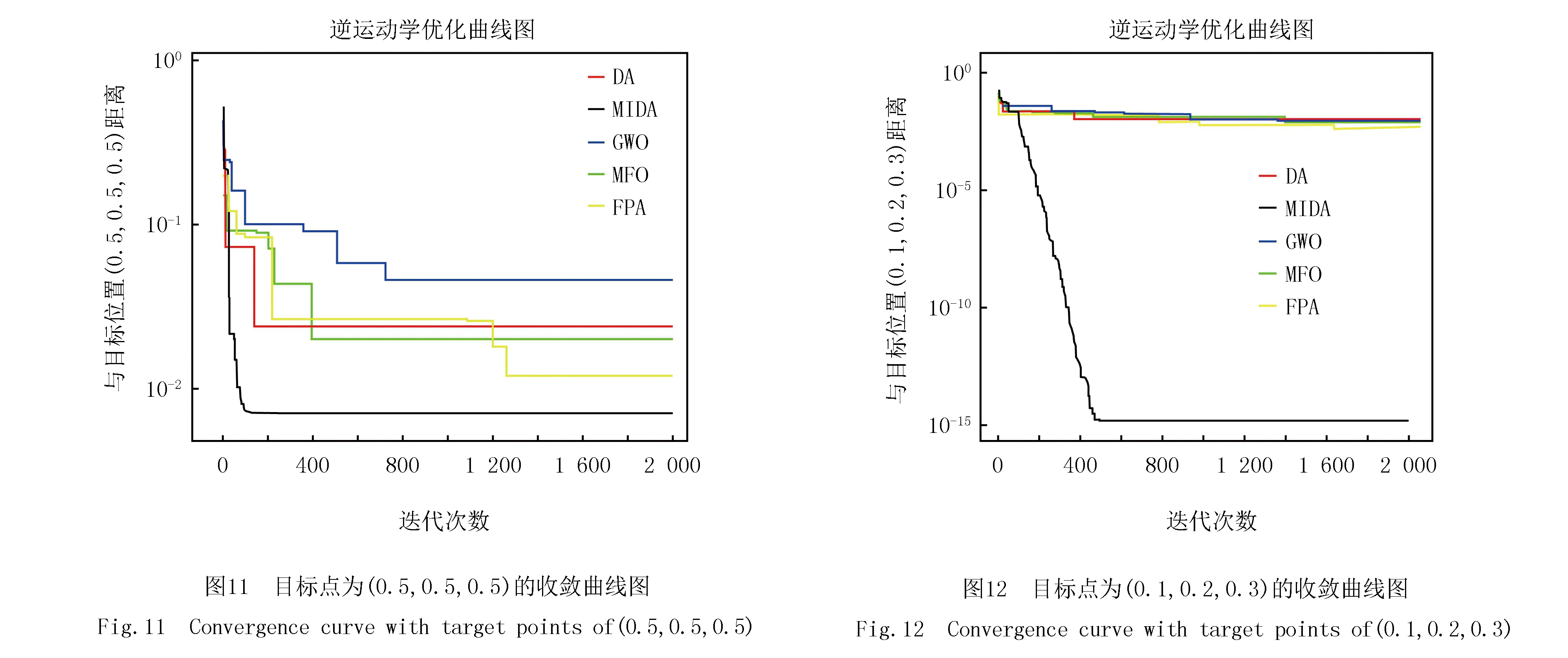
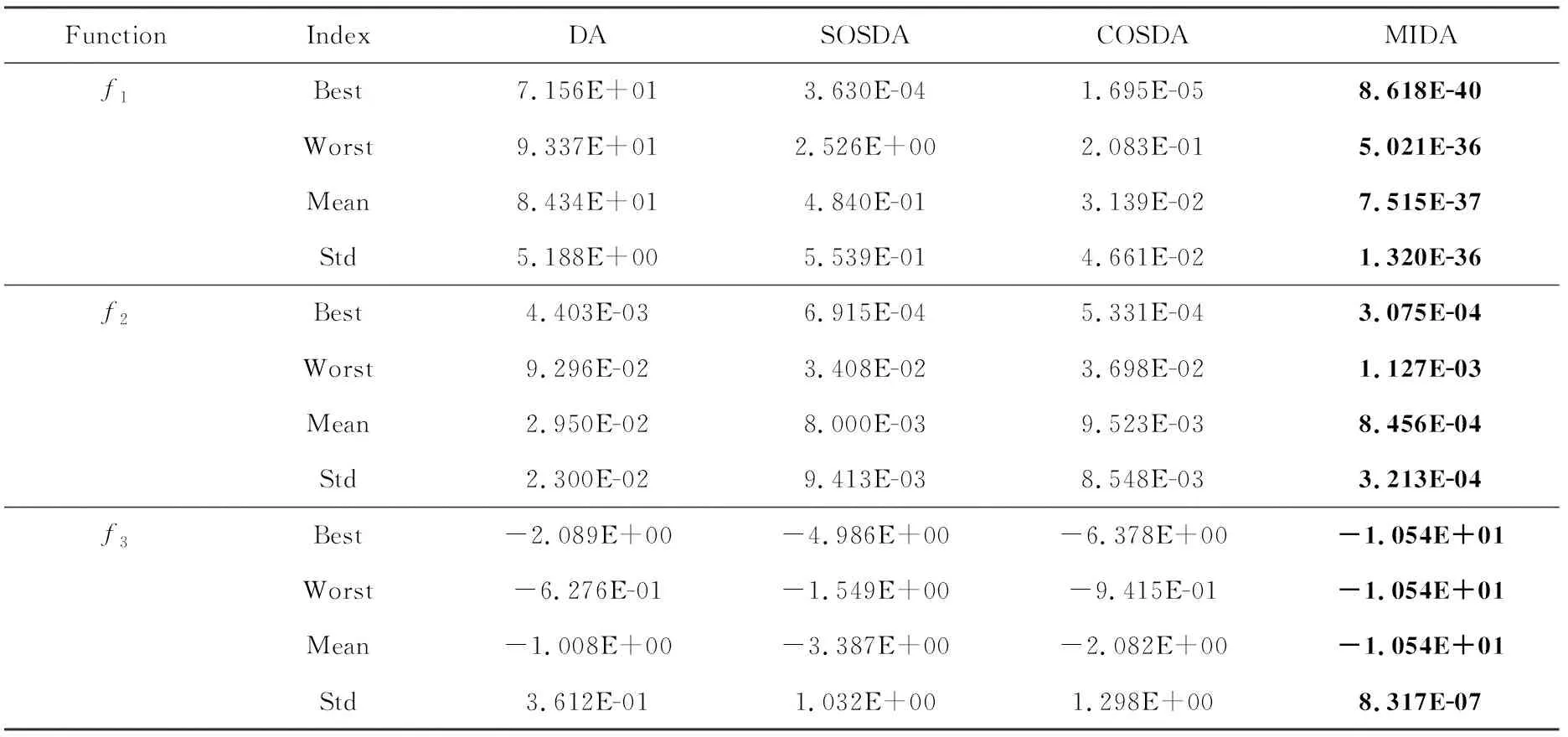
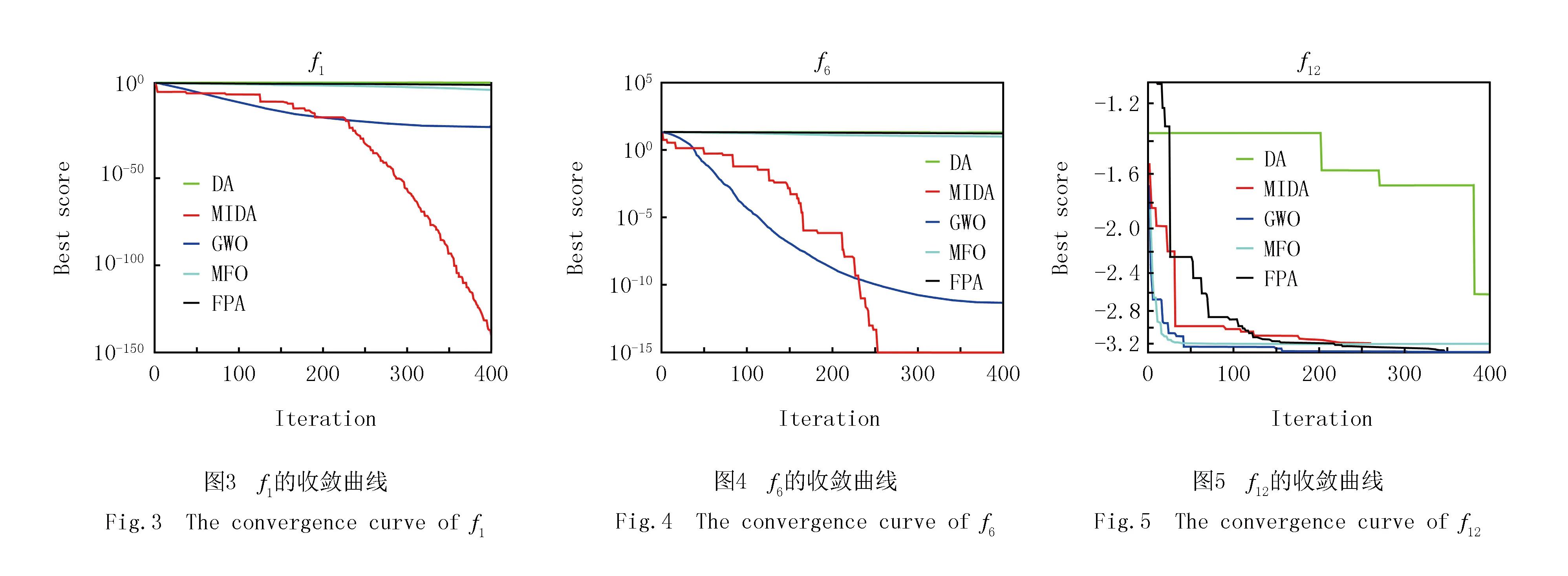
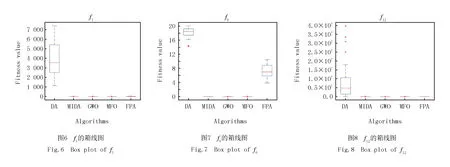
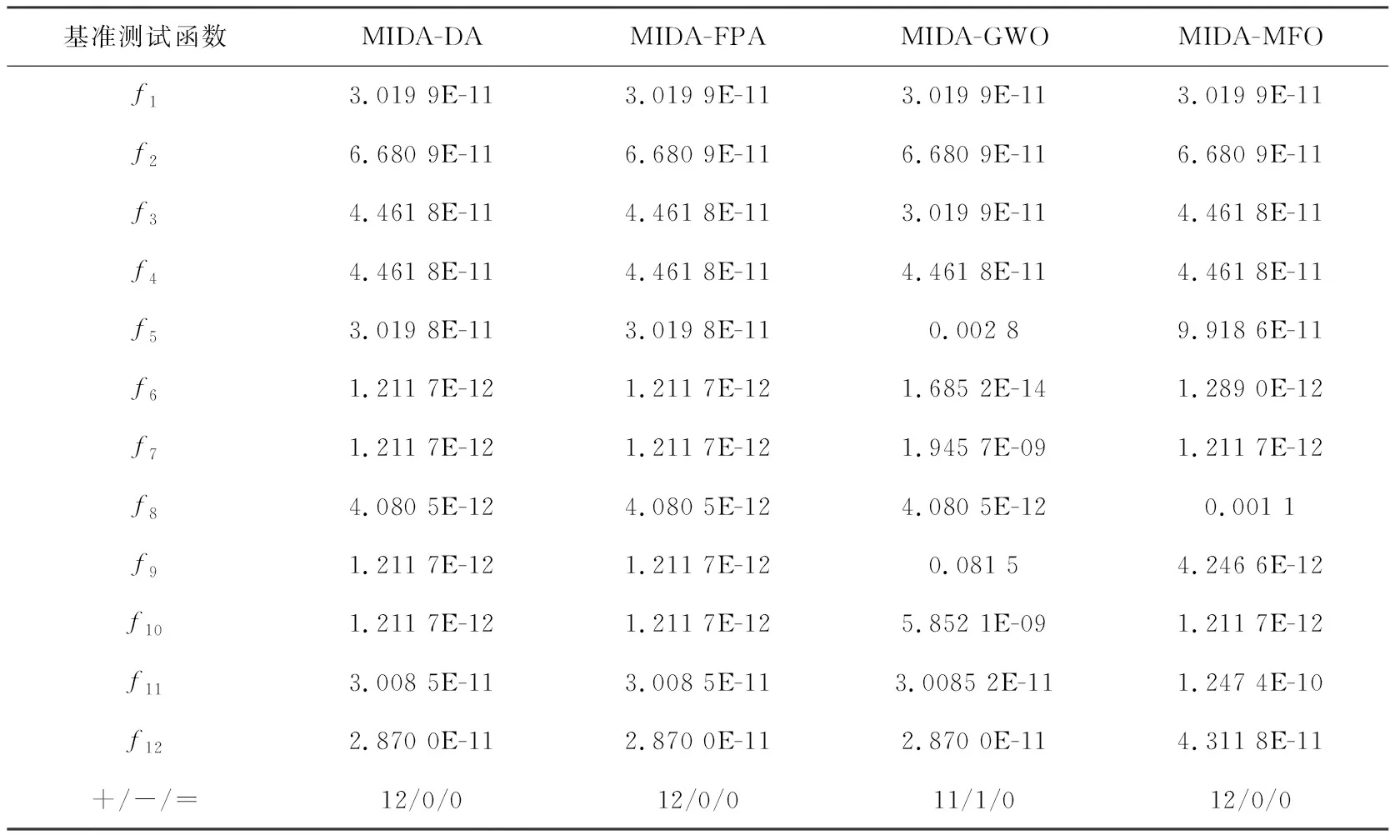
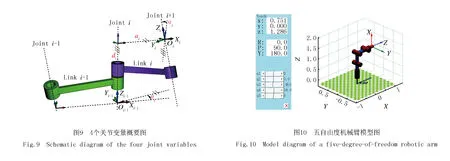
8. ifXnew

9. 取优解为新的蜻蜓位置

10. else

11. 通过式(12)更新蜻蜓位置

12. endif

13. 检查是否达到迭代次数

14. endwhile

2.5 算法复杂度分析

空间复杂度指的是完成算法需要的空间,Logistic初始化,互利共栖阶段与余弦扰动并未增加算法所需的空间,因此DA与MIDA的空间复杂度均取决于种群数量N与维度d,为O(N×d).

时间复杂度是指算法运行时间,取决于迭代次数i,种群个数n等,DA的时间复杂度为O(i(n1+n2(n3+d1+d2))).

其中各参数含义依次为:i为总迭代次数;n1为计算所有个体的适应度值的循环;n2为计算蜻蜓邻居所需的循环;n3为邻居个体数的存储循环,d1为越界处理;d2为存在邻居时,超出位移最大值的处理循环.其中n1,n2,n3均为初始种群数,d1,d2为个体的维度,其值为极小的常数.

因为d1,d2为极小的常数,且n1,n2的值为种群数量N.故DA的时间复杂度可简化为O(i(N+Nn3))=O(iNn3).

在MIDA中,Logistic初始化与随机初始化本质相同,未增加算法的复杂度,互利与共栖应用于原算法公式,余弦扰动与位置更新处于同一级,均未增加算法的复杂度,因此MIDA的时间复杂度也是O(iNn3).

2.6 正交实验检测

为证明上述改进对基本的蜻蜓算法均有所改善,本小节用基本蜻蜓算法(DA),融合共生生物搜索的蜻蜓算法(SOSDA),基于余弦扰动的蜻蜓算法(COSDA)与多策略改进的蜻蜓算法(MIDA)进行比较.高维单峰(f1)、高维多峰(f2)以及定维多峰测试函数(f3)各取1个用来测试其性能.

其中DA如2.2小节所示;MIDA如2.4小节所示;SOSDA即基本蜻蜓算法中式(3)替换为式(11),COSDA即基本蜻蜓算法最后加入式(12).

4个对比算法对表2的3种函数进行优化,每次迭代400代,并独立运行30次,优化得出的最小值、最大值、平均值与方差如表3所示,本文算法的结果见黑体部分.

表2 测试函数详细信息

表3 实验结果

由表3可以看出,无论是SOSDA还是COSDA,他们对函数的优化效果都比DA好,而MIDA更是远优于其他3种算法,在对f1的优化中,效果比其他算法高出30个数量级.因此,本文所提出的改进方法的可行性与有效性得到了证明.

3 仿真实验和结果分析

本文通过12个基准测试函数来测试改进算法,同时将其应用在逆运动学中求解五自由度机械臂的参数.为避免实验结果的偶然性,本文对算法独立运行400次,种群个数均为30,同时统计并分析它们的最佳值、最差值、平均值和标准差.

本实验运行环境为Windows10,处理器:Intel(R)Core(TM)i5-5200U @2.20 GHz;

内存:4.00 GB.所有算法代码都在MATLAB R2018b中运行.

3.1 基准函数测试

本文采用了12个基准函数,其中高维单峰(f1～f4)、高维多峰(f5～f8)以及定维多峰(f9～f12)测试函数各取4个来测试其性能如何.同时与灰狼算法［10］(Grey Wolf Optimizer,GWO),花授粉算法［11］(Flower Pollination Algorithm,FPA),飞蛾扑火算法［12］(Moth-flame Optimization Algorithm,MFO)进行对比与分析.

算法的参数为DA:r∈［0,1］,β=1.5,MIDA:μ=3.999,β=1.5,r∈［0,1］,bf1=1,φ∈［-1,1］,FPA:p=0.1,GWO:r1,r2∈［0,1］,A=2ar1-a,C=2r2,MFO:b=1,t∈［-1,1］.基准函数见附表Ⅰ.

3.2 实验结果分析

用DA,FPA,GWO,MFO,MIDA这5个算法对12个基准函数进行仿真,迭代次数均为400代,独立运行30次得出的最优值(Best)、最差值(Worst)、平均值(Mean)和方差(Std)如附表Ⅱ所示,最优结果见黑体部分.

每个函数优化出的最优值已经加粗,为了更方便明显地比较各算法的收敛速度,下面给出算法收敛曲线图.为比较各个算法的稳定性,同时给出他们的箱线图.由于篇幅限制,高维单峰、高维多峰与定维多峰测试函数各一张,如图3～8为f1,f6,f12的收敛曲线及与之对应的箱线图.

由附表Ⅱ的实验结果可知,MIDA相较于其他4种算法,对高维单峰的函数优化极为显著,不仅效果最好,且优化精度高出其他算法近百个数量级.对于高维多峰函数的优化也稳居第一.在对定维多峰的函数优化中,收敛最优值也稳定第一,但是在稳定性方面不如GWO.

由图3和图6可以看出,相较于其他4种算法,MIDA对函数的优化有压倒性的优势,其他4种算法的收敛已经趋于稳定,由此可见其他4种算法具有一定的局限.而MIDA的下降趋势在400代仍旧明显.由附表Ⅱ的实验结果也能看出它强大的收敛能力,不仅仅是对f1,MIDA对所有的高维单峰函数的收敛精度远高于其他算法,同时标准差更小,表明MIDA的稳定性极高.

由图4和图7可知,MIDA的收敛精度更高,且收敛速度更快,同时由附表Ⅱ的标准差栏目中可以看出MIDA所得出的值相当低,由此可知MIDA的稳定性极高.在对高维多峰函数优化时,MIDA得出的最优值都是最好的,由此可见MIDA的寻优性能极佳.

由图5可以得知,MIDA对个别函数的收敛能力与其他4种算法接近,但是从附表Ⅱ可以看出MIDA的精准度更高,优化得出的最优值更好.MIDA对f12的收敛速度略低于GWO,但是MIDA最终的最优值与连续运行30次所得的方差更优于GWO,可见MIDA在函数的优化中处于遥遥领先地位.附表Ⅱ中的数值也能显示MIDA在对定维多峰函数优化时总能保持最佳的收敛性能.图6～8的箱线图表明MIDA的稳定性明显优于其他4种算法.

3.3 Wilcoxon秩和检验

在评估元启发式算法的性能时,只比较均值与最优值是不够的［13］.因此,为证明所提出算法的结果与其他算法是否在统计上有显著不同.需要进行统计测试.为了减少犯第一类错误的概率,本文先通过Kruskal-Wallis检验进行多组比较,判断5种算法是否有显著性差异.

实验结果得出检验值p=9.02E-29<0.05,说明在显著水平0.05下,检验拒绝了原假设,即5种算法具有显著性差异.

在具有显著性差异的基础上,通过显著水平为0.05的Wilcoxon秩和检验进行多重比较.Wilcoxon秩和检验的目的是用于比较两个独立样本的差异.在算法中用于比较两种算法有没有差异,有差异才可以比较优劣.在Wilcoxon秩和检验中,用MIDA和其他算法进行对比,实验结果得出的p值小于0.05,则证明两种算法差异有统计学意义.表4为MIDA与其他算法采用最优值进行秩和检验的结果.“+”“-”“=”分别为本文算法与比较算法的成绩相比是好/差/相等.秩和检验显示,当显著性水平为0.05时,MIDA与其他4种算法具有显著性差异.

表4 Wilcocon秩和检验实验结果

3.4 求解逆运动学中五自由度机械臂的参数问题

从上一小节MIDA对函数的优化中可以得知,MIDA拥有较强的寻优性能,接下来利用MIDA解决五自由度机械臂逆运动学的求解.在机械臂的运动控制中,可以分为正运动学与逆运动学,正运动学是给定机器人关节变量的取值来确定末端执行器的位置和姿态.逆运动学是根据给定的末端执行器的位置和姿态来确定机器人关节变量的数值.

DH 建模方法［14］是由DENAVIT和HARTENBERG提出的一种建模方法,主要用在机器人运动学上.此方法仅仅通过4个参数便可以确定机械臂的各个节点的位姿状态.对每个关节建立坐标系,关节总是绕着z轴旋转,同时,4个关节变量可以确定机械臂的位置.其中θ表示绕z轴的旋转角度,d表示在z轴上两条相邻公垂线的距离,a表示每一条公垂线的长度,也叫做关节变量,a表示两个相邻z轴的角度,又称为关节扭转.图9标注了各个关节变量的信息.

本文使用标准型D-H参数(STD)建模［15］,其建模步骤如下:

(1)绕zi-1轴旋转θi,使xi-1与xi平行;

(2)沿zi-1轴平移di,使xi-1与xi重合;

(3)沿zi轴平移ai,使zi-1与zi重合;

(4)绕xi轴旋转αi,使zi-1与zi共线;

通过每个旋转和平移的步骤得到的旋转矩阵:

(13)

(14)

由此可以得到变换矩阵:

(15)

以图10的五自由度机械臂为例,选定空间中的一点(x,y,z),通过MIDA,优化得出最佳的4个关节变量.首先通过模型图建立每个节点的坐标系,然后得出D-H参数表如表5所示.

D-H参数表的填写方式如下:

(1)ai：沿Xi轴方向,从Zi移动到Zi+1的距离.

(2)αi：从Zi旋转到Zi+1的角度,转轴为Zi,遵循右手定则,以Xi方向为大拇指方向.即杆i与杆i+1的夹角.

(3)di：沿Zi轴从Xi+1移动到Xi的距离.

(4)θi：绕Zi轴从Xi+1转到Xi的角度.

表5 五自由度机械臂D-H参数

(16)

其中(Px,Py,Pz)表示机械臂末端位姿相对基座坐标系的位置.

(17)

在上述公式中,通过各个θ的值可以确定机械臂末端的位姿,这便是正运动学.而已知末端点的坐标(x,y,z)来求得各个角度是相当复杂的,这便是逆运动学［16］,本章使用MIDA来求解逆运动学这一复杂问题.

适应度函数是启发式优化算法的重要内容之一,通过适应度函数值,算法才能不断地更新最佳值.在本研究中,使用欧氏距离作为适应度函数［17］.利用MIDA获得了最接近预定目标点的位置.其适应度函数f如下:

(18)

其中,(x,y,z)与(Px,Py,Pz)分别为目标点的空间位置与机械臂末端位姿的空间位置.

3.5 实验结果

本文使用MIDA与DA,GWO, FPA,MFO同时对上述问题进行求解.设定目标位置为(0.5,0.5,0.5),独立运行30次,所得的最优值、最差值、平均值和标准差如表6黑体部分.

表6 实验结果

实验结果显示,MIDA对五自由度机械臂逆运动学的优化稳定性略低于FPA,但是在优化效果方面稳居第一,MIDA优化所得的最优结果比MFO高出10.12%,比GWO高出35%,更是比FPA与GWO高出一个数量级.FPA的稳定性虽然与MIDA接近,但是最优值的优化效果远不及MIDA.图11、12为MIDA针对两个目标点的优化收敛曲线图,可以得知改进算法MIDA相较其他4个对比算法有显著优势.本文的实验结果表明MIDA在函数方面的优化效果极佳,同时在逆运动学方面的求解优势极为显著.

4 结 论

本文通过对初始种群的选取,使算法更快定位到最优解区域;对迭代寻优过程进行优化,使算法在勘探和开发过程更加全面;对结果扰动变异,使算法跳脱局部解,在这3个方面对蜻蜓算法进行了优化,并通过12个基准函数的测试与求解逆运动学这一实际应用证明了MIDA具有更强的收敛能力、更快的收敛速度和极佳的稳定性.在优化效果方面精度高出10.12%.在实际应用中,需要机械臂准确高效获得抓取目标物品所需的关节变量.但是在本文中只应用了五自由度的机械臂,在空间中的搜索能力有限.未来将会对经典的七自由度机械臂［18］,甚至更多自由度的机械臂进行研究.

附 录

附表Ⅰ、Ⅱ见电子版(DOI:10.16366/j.cnki.1000-2367.2023.05.005).