助飞运载器螺旋传动失效的机理研究
杜永刚, 王雪松, 万志华
(中国空间技术研究院 兰州空间技术物理研究所, 甘肃 兰州 730000)
0 引言
为了得到更高的配弹容量和方便储运,现代导弹的翼面在发射之前均处于折叠状态[1-2],如果导弹的翼面无法正常展开到位,则导弹无法正常飞行,因此导弹的翼面折叠及其展开技术是其关键技术,也是内埋式导弹的关键件和研究重点[3-5]。由于导弹或运载器在飞行时的气动力对折叠翼的外形有着重要制约[6],一种小体积的逆向螺旋传动机构就受到了设计人员的重视,近年才被大量应用在导弹、运载器的展开机构中[7]。某运载器在离开水面后需要展开舵面,其展开机构采用了这种逆向螺旋传动机构。通过螺旋形的滑动副,展开机构将直线运动转换为旋转运动,从而实现舵的展开。
研究者在多次实验中发现这种传动机构中的滑动副偶尔出现卡涩的故障。所有的实验零件均按工艺进行严格清洗,并在洁净环境下完成传动机构的装配。实验前,测试人员也按程序检查了所有参与实验的传动机构,所有螺旋传动机构的运动均良好无卡涩,因此这种卡涩故障和滑动副的配合、安装以及多余物等底事件无关。通过排除法,故障树上只存在“传动接触面性质改变”的唯一底事件。舵的展开时间不超过几十毫秒,且承受很大的展开载荷,因此其传动接触面的相对运动必然是高速、大接触力的滑动,其滑动摩擦将产生接触面的温升现象[8]。有研究发现温升会加剧接触面的凿削效应,而凿削夹杂又导致接触面的严重破坏[9-11],因此初步定位螺旋传动失效和接触面的摩擦及温升直接相关。
迄今为止,对于这种逆向螺旋传动的研究只局限于其结构强度,而缺乏摩擦及温升对其传动影响的研究,因此本文建立了高速、大载荷并耦合摩擦热的螺旋传动的数值模型,通过分析计算结果和实验现象,揭示了大载荷下的接触面摩擦和温升对这种螺旋传动的影响及其产生传动失效的机理。
1 传动原理及模型设定
1.1 传动原理
通过将直线运动转换为旋转运动,运载器的螺旋传动机构实现舵的旋转展开,火工品是该机构的展开动力源,这种展开机构的主要构成如图1所示,逆向螺旋传动机构是其核心组成。逆向螺旋传动机构由一个旋转轴和一个推杆组成,其构成如图2所示。

图1 舵展开机构的主要组成
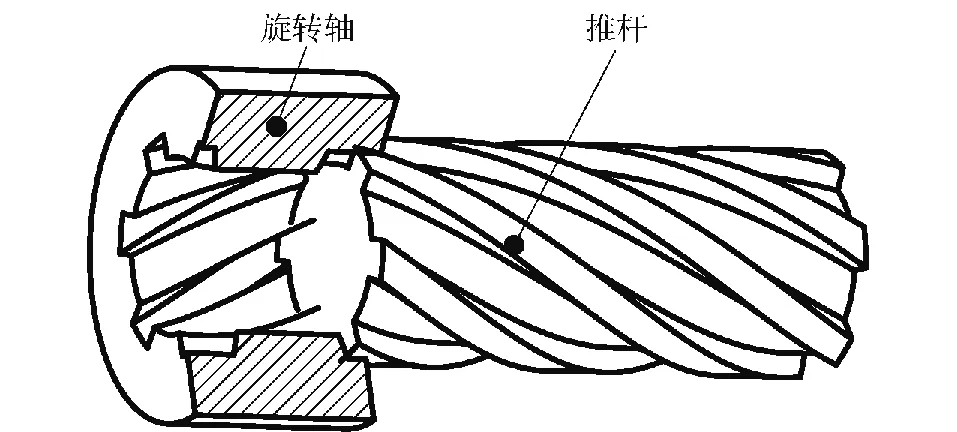
图2 传动机构的构成
旋转轴的内孔加工有螺旋槽,而推杆的外圆柱面上加工有螺旋形的筋,筋啮合在旋转轴的螺旋槽内,如其螺旋升角大于摩擦角,推杆可直线驱动旋转轴实现旋转运动。筋与螺旋槽的啮合面形成传动的滑动副,当该滑动副为高速的相对运动时,摩擦及温升对其接触表面的作用机制是本文的主要研究目标。下面将围绕该研究目标建立数值模型的网格、材料模型、接触面的热耦合模型以及设定边界条件。
1.2 模型设定
为简化计算模型,作如下设定:
1) 旋转轴的转动副不是本文的研究内容,因此将其简化为单旋转自由度的点。同理,将推杆的滑动副简化为单平动自由度的点。
2) 为了提高计算效率,将推杆和火工品连接的部分截除。同理,将旋转轴和舵连接的部分截除。
3) 火工装置的驱动力是瞬间上升至极高值,其测试曲线可被近似成阶跃响应,由于这种急剧变化的驱动载荷使计算难于收敛,简化驱动力为恒定值,其作用时间为火工品的爆燃时间,这种简化可保证计算的顺利完成。
4) 模型的起始温度为20 ℃。
5) 不计重力场的影响。
2 螺旋传动的模型
2.1 模型框架
根据研究目标,本文建立了数值模型的框架,框架如图3所示。计算模型的主体由四部分组成:有限元网格、材料模型、接触热耦合模型以及计算边界条件。材料模型表达热应变、总应变、总应力场的计算及其模型参数;接触面热耦合模型表达摩擦耗散能、接触面之间的热传导以及接触面温度场的计算及其模型参数;计算边界条件包括运动约束及其载荷。基于该框架,本文利用ADINA软件编写了材料模型、接触热耦合模型以及边界条件的IN计算程序以及NAS网格文件。
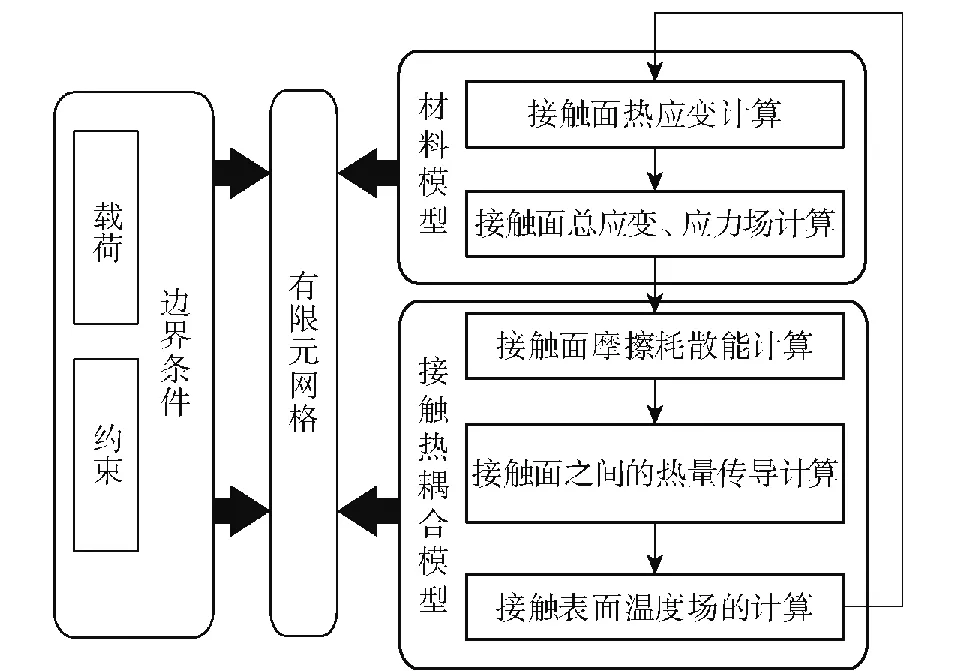
图3 模型框架
2.2 有限元网格
表1列出了传动零件的几何模型尺寸。推杆和旋转轴的网格均采用八节点六面体单元,筋与螺旋槽的接触面是计算传动的关键部位,该部位采用了细化网格。建立的网格模型如图4所示,推杆模型有12 096个单元,旋转轴模型有3 600个单元,推杆接触面有2 106个面单元,旋转轴接触面有528个面单元,为保证模型的计算精度,各单元尺寸均小于1 mm。

表1 模型的几何参数
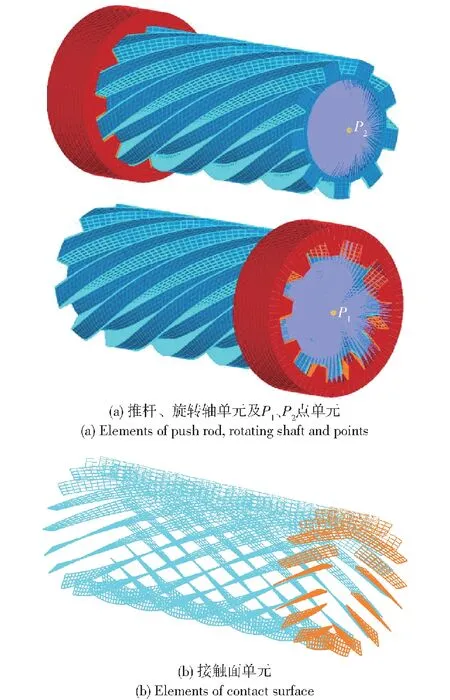
图4 有限元网格模型
如图4所示,将转动副简化为点单元P1,并用RIGLINK命令将其与旋转轴连接;将滑动副简化为点单元P2,并将其与推杆用RIGLINK命令连接。
2.3 材料模型
旋转轴和推杆的材料都是高强合金钢30CrMnSiA,设定这种金属为各向同性的热弹性材料模型,材料密度ρ=7.8 g/cm3。热应力计算常采用该热弹性材料模型,用于接触面的总应力和温度分布的计算。BATHE[12-13]表达该材料的连续方程为
(1)
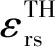
(2)

(3)
T为接触面的温度,T0为接触面的初始温度,α(T)为温度为T时的热膨胀系数,Tref为参考温度,本文取Tref=20 ℃;α(T0)为温度T0时的热膨胀系数。对表2中的数据进行分段线性插值,得到不同温度点的弹性模量CTH和热膨胀系数α(T),因此这种热弹性材料的模型参数在表2中完备。表2~表4中的数据均引自Total Materia数据库及材料手册[14-15]。
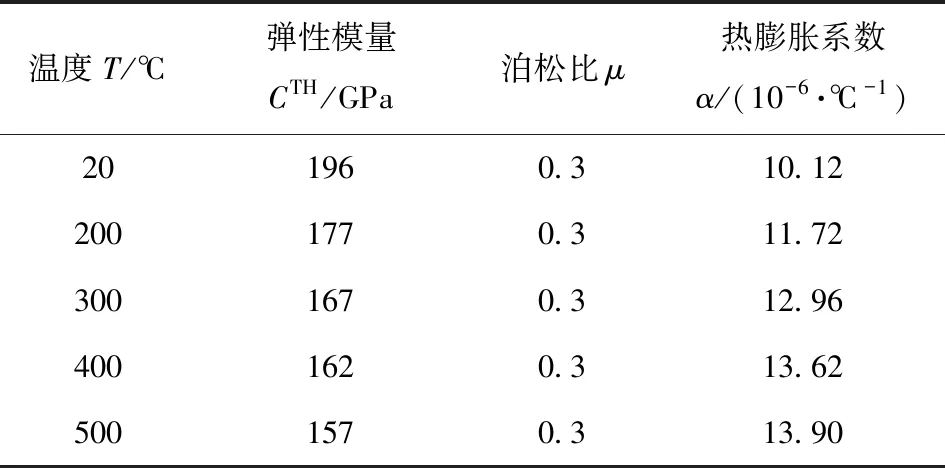
表2 30CrMnSiA的热弹性材料参数
2.4 接触面热耦合模型
接触面分为接触体接触面和目标体接触面,其中接触体是推杆,目标体是旋转轴,这种设置可提高计算的收敛速度。接触面上的摩擦热被分别传入接触体和目标体,其示意图如图5所示。图5中qSC为接触体表面的热流,qST为目标体接触表面的热流,TC和TT分别为接触体和目标体的温度。>

图5 接触面之间的热量传导
多物理特征的接触算法[16-17]能够计算接触表面的摩擦耗散能及其产生的摩擦热量,也可计算接触面之间的热量传导。该算法引入影响热传导的接触间隙,能够准确模拟出研究对象的实际状态。接触表面的摩擦耗散能可用下面的增量方程表达:
(4)

摩擦热量在接触面之间的传导计算公式为
qSC=δh(TT-TC)
qST=δh(TC-TT)
(5)
式中:h为与温度相关的热传导系数;δ为与接触应力相关的间隙系数,计算程序根据接触应力调整其数值,且满足0<δ<1,它是无量纲参数。对表3中的数据进行线性插值后可得到h,该插值由主程序自动计算。由于式(5)中存在间隙系数δ,两个接触面的温度场必然存在差异。
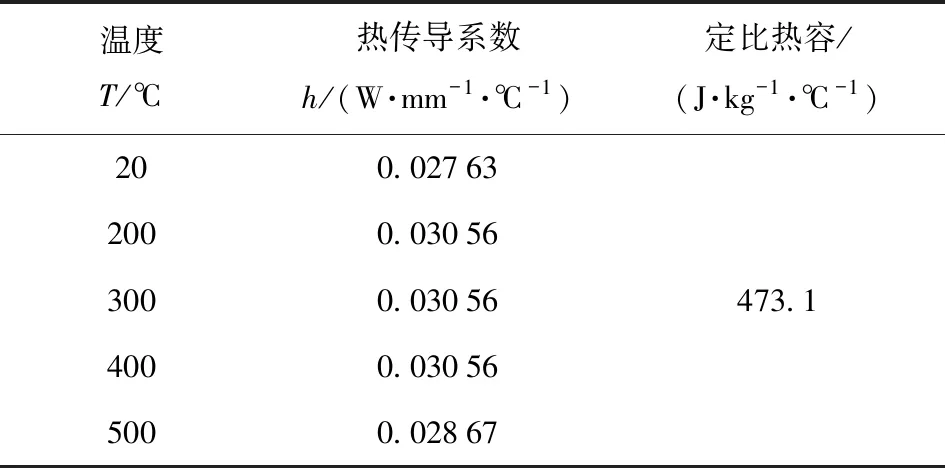
表3 30CrMnSiA的热物理参数
摩擦耗散能量在接触面上产生热流的计算公式为
qSC=fcEf
qST=fTEf
(6)
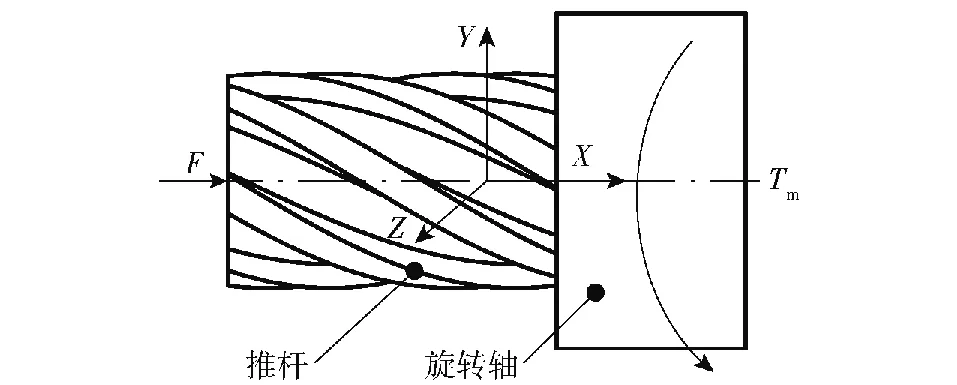
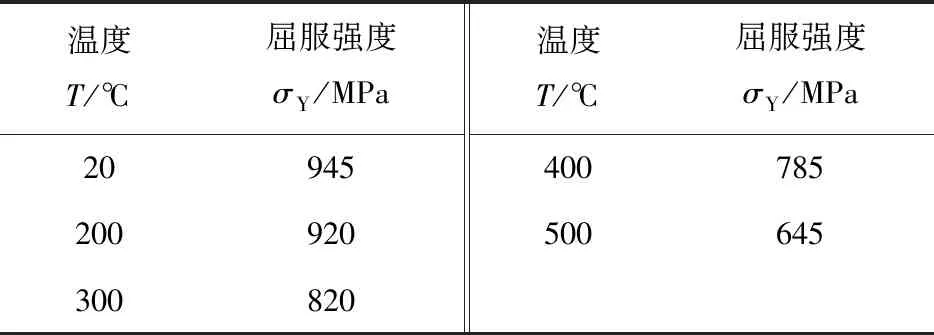
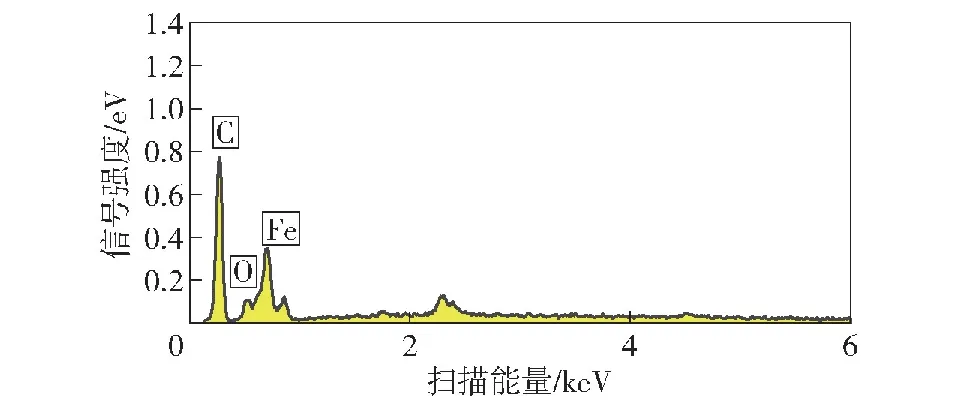
式中:fc和fT分别为接触体和目标体表面的能量损失因子,0 复杂螺旋结构导致其接触面的库伦摩擦系数只能达到0.5。为了得到一个较宽范围内的计算结果,本文取库伦摩擦系数为0.04~0.6之间的系列数,模型中设定接触面的库伦摩擦系数为不变量,并根据系列数进行多次计算。上述接触面热耦合模型的参数如表3所示。 模型的边界条件有约束和载荷。约束边界设定旋转轴具有X轴的旋转自由度,并限制其X轴、Y轴、Z轴方向的平动自由度,以及Y轴、Z轴方向的旋转自由度。约束边界设定推杆有X轴方向的平动自由度,并限制其X轴、Y轴、Z轴的旋转自由度和Y轴、Z轴方向的平动自由度。 载荷分为驱动和负载。一个直线力F施加在推杆上,它驱动推杆朝+X轴方向平动,而旋转力矩载荷Tm施加在旋转轴上,它是阻止旋转轴转动的负载,这两个载荷产生的运动趋势相反。直线力载荷F=30 000 N,旋转力矩载荷Tm=80 N·m。图6为载荷在模型上的施加关系。 图6 施加的载荷 由于螺旋传动机构被火工品直接驱动,该机构是一种高速传动机构,其计算步长宜采用小量设置。设置模型的计算步长为1×10-5s,计算步数为 150步,计算总时间为1.5 ms。依据上述计算理论、模型参数以及模型边界条件,本文采用ADINA软件编写计算程序和网格文件,并完成传动模型的数值模拟计算。由于该传动接触具有大接触应力、高速滑动的特点,其计算难于收敛,本文采用易于收敛的Bathe隐式时间积分方法求解,同时利用ATS算法控制计算步长,以提高计算效率和稳定性[18]。 图7为传动接触面的应力分布云图和温度分布云图。图7中的数据表明:推杆接触表面的最高应力值为699.4 MPa,旋转轴接触表面的最高应力值为566.5 MPa,推杆接触表面的最高温度值为454.3 ℃,旋转轴接触表面的最高温度值为 444.4 ℃。图8为推杆的运动速度曲线,图9为接触面温度在传动过程中的变化曲线,图中的数据表明机构的工作时间为1.24 ms,推杆的最高速度为164.6 m/s。 图7 接触表面的温度和应力分布 图8 推杆的速度曲线 本文还计算了摩擦系数和接触面温度之间的规律,其关系曲线如图10所示,从中看出接触表面的温度随着摩擦系数的增大而升高,两者呈现正比的关系。 图10 摩擦系数和接触面温度的关系曲线 近年来,导弹、运载器开始采用一种小体积的逆向螺旋传动机构。设计人员只关注其结构强度核算,但没有认识摩擦及温升对其传动的影响。通过该传动的热机耦合计算,本文研究了其传动接触面的热、力学等特性,文中的内容对该类产品的开发具有参考价值和指导意义。本文对以下观点进行了讨论。 1) 螺旋传动的失效部位。图7表明接触面是传动零件的极限应力部位,推杆的接触极限应力高于螺旋轴的值,因此推杆的螺旋形接触面首先被损坏,这种差异可能源自它们的结构。 接触算法较好表达了热量在接触面之间的传递过程和原理。由于接触应力确定间隙系数,传入推杆接触面的热量必然大于旋转轴的热量,推杆接触面的温升也高于螺旋轴的温升,图7的温度云图及图11证实了该现象,因此摩擦热的主要影响部位也是推杆的螺旋形接触面。 图11 推杆的筋部位照片 2) 摩擦导致传动失效的作用机制。图8的数据说明这种螺旋传动具有很高的运动速度,高速的大载荷摩擦必然导致传动接触面的高温升。随着温度的升高,合金钢的屈服强度呈现降低的趋势[19]。根据强度理论,当金属材料的极限应力超过其屈服强度时接触材料将被破坏[20]。表4列出了30CrMnSiA在高温段下的屈服强度。由表4可见:当温度达到500 ℃时,这种材料的屈服强度已经降低至645 MPa,该数值已经接近接触面的极限应力值,甚至局部的接触应力值已经超过了该材料的屈服强度;30CrMnSiA在200 ℃下的屈服强度为σY=920 MPa,其接触极限应力为σM=699.4 MPa,因此其安全系数为η=σY/σM=1.31,该值接近设计规范中的极限值[21]。再根据摩擦系数和温度的关系曲线,本文推断出该螺旋传动接触表面的库伦摩擦系数不能超过0.2。 表4 30CrMnSiA在不同温度下的屈服强度 图10表明,接触表面的温度随着摩擦系数的增大而逐步平缓,随着摩擦系数的增大,其对温升的影响逐步减弱,摩擦产生的热量趋于稳定。高速滑动摩擦副的局部高温会严重影响接触面的力学特性[22-23]。该螺旋传动接触面材料的应力超过其屈服强度后,其接触面将产生大形变,因此高温软化的接触面在巨大摩擦力的机械作用下,其接触材料将被持续破坏[24],这种高温软化机制可参考内弹道烧蚀磨损[25]。 为了进一步证实这个机理,研究人员检查了实验产品,发现实验产品的传动接触面上均存在不同程度的类似烧蚀的痕迹。推杆的筋部位照片如 图11 所示,接触面上棕黑色的痕迹已经被牢固烧结在金属表层内。图12为该类烧蚀部位材料的能谱分析结果,谱图表明烧蚀层的主要成分为炭化物。所有的实验产品均按工艺要求进行严格清洗,其装配环境也为洁净间环境,因此润滑脂是传动结构上的唯一有机物质,其在高温下形成了炭化物。根据润滑脂厂家的产品数据,该润滑脂的炭化温度约为400 ℃,由此间接证实了接触面存在由摩擦导致的高温,也可推断出该类烧蚀部位的温度不低于 400 ℃。 对类烧蚀部位放大后,也明显观察到了凿削的破坏痕迹(见图11),直接说明在高速的传动过程中,高温软化的接触面存在被摩擦力破坏的事件。由于早期产品受到工艺的限制,其螺旋形接触面的粗糙度和不规则性远劣于本文中的理想模型,接触面上的局部温度和摩擦力也必然高于理论计算的数据。 图12 烧蚀部位材料的能谱分析图 通过对底事件的排除及实验现象的分析,研究者推测早期产品发生卡涩的主要原因为:1)高温软化的接触面材料被摩擦力破坏并脱落,脱落物在配合间隙中形成夹杂并阻碍了运动;2)两个接触体采用了相同的金属材料,其接触面上的高温使滑动副咬合。卡涩故障也可能是这两个原因综合作用的结果。 综合以上分析,工程实践中需要控制该传动滑动副的摩擦系数。工程中习惯采用轮廓算术平均偏差值(Ra值)表征材料表面的光滑程度。根据经验,该滑动副的粗糙度值不宜大于Ra3.2,但过低的粗糙度Ra值会大幅度增加制造成本,因此建议粗糙度值取Ra1.6~Ra3.2,并根据实际的接触工况进行调整。 1) 在大载荷、高速的传动下,粗糙接触表面的高速摩擦会产生大量的热,该热量导致传动副表面的温升,实验件的类烧蚀痕迹及其炭化成分也证实了这种温升现象的存在。烧蚀部位的凿削痕迹也表明接触面的金属薄层上存在破坏事件。 2) 可以推测,早期产品发生卡涩的原因与接触面的高温升有关,在后期产品的开发中,设计人员通过优化成型工艺和润滑设计缓解了这种温升效应,也解决了实际的工程问题。 3) 这种螺旋传动是高速、大接触应力的摩擦滑动,因此模型的接触单元采用了低阶、小尺寸的接触单元,这种接触单元的设定减少了接触计算的误差,也改善了接触运算的收敛性,从而使仿真模型能得到一个较为准确和稳定的计算结果。2.5 载荷与边界条件
3 数值计算与结果讨论
3.1 计算



3.2 结果讨论

4 结论

