考虑泄漏的无杆式高压气动弹射器内弹道精确建模及试验

王雪琴, 马吴宁, 马大为, 王尚龙, 张震东

(1.南京理工大学 机械工程学院, 江苏 南京 210094; 2.陆军研究院 工程设计研究所, 江苏 南京 210016)

0 引言

随着现代空天侦察技术的快速发展,对导弹隐蔽生存提出了更高要求,因而冷发射方式得到越来越广泛的应用[1]。目前冷发射方式主要有燃气式、压缩空气式、液压式和电磁式等[2]。其中压缩空气式具有红外暴露特征小、环境适应性好和设备重复利用率高等优点,能极大地降低发射阵地的红外特征,提高生存能力[3]。但也带来了极端工况下基于理想气体的热力性质参数较实际值会产生很大偏差,进而影响弹道参数真实性的问题[4]。

国外对于空气气体状态方程的研究,经历了从理想气体状态方程,到利用统计学方法考虑分子间作用力后导出的各种真实气体状态方程(范德瓦尔斯方程、维里方程、Redlieh-Kwong方程、Soave-Redlieh-Kwong方程[5]、Peng-Robinson方程[6]等),再到针对空气的热物性质进行了持续十多年的实验数据测量,并由实验数据拟合出标准干空气热力学状态方程的发展过程。其中,由实验数据拟合的标准干空气热力学状态方程适用范围最广:温度60～2 000 K,压力0～2 000 MPa[7]。

国内关于气动弹射内弹道建模研究,主要以理想气体、绝热和零泄漏假设[8-14]为主,只有较少数学者开展了考虑真实气体效应的弹射内弹道建模方法研究。Ren等[15]、杨风波等[4,16]、Yang等[17]提出一种高压空气两级三气缸弹射装置,基于改进的对应态维里方程,建立了考虑真实气体效应的内弹道模型并进行了数值计算,研究表明高压空气的综合做功能力偏离理想气体,真实气体效应研究必不可少。任锐等[18]研究了一种以压缩空气为动力源、油液为传动介质,具备油液自缓冲结构的多级气动液压弹射装置的弹射性能,基于真实气体状态方程——维里方程,建立了描述多级气动液压弹射过程的数学模型。姚琳等[3]提出一种新型高压空气驱动无杆式气缸弹射装置,引入真实气体状态方程——Redlieh-Kwong状态方程,建立了考虑真实气体效应、泄漏率为定值的无杆式气缸弹射装置内弹道模型。

上述研究大多基于理想气体、零泄漏假设及非真实开阀过程的内弹道理论模型,或者基于真实气体假设、非真实开阀过程且不考虑动态的内弹道理论模型。此外上述研究中使用的各种真实气体状态方程都只适用于一定压力和温度范围。将真实气体效应、动态泄漏及真实开阀规律同时考虑的内弹道理论模型研究鲜有报道。

本文针对压力和温度大范围变化、固有结构存在一定泄漏的双缸对称无杆式高压气动弹射器开展动态泄漏测试试验,基于美国国家标准技术研究所(NIST)发布的标准干空气热力学状态方程,分别按理想气体和真实气体假设对比计算泄漏率,并拟合泄漏率随压力、行程变化的经验公式;基于高压空气的真实热力性质参数,建立考虑动态泄漏、真实气体效应及真实开阀规律的精确内弹道模型,分别对考虑泄漏和不考虑泄漏两种工况进行数值求解。对两种工况下的数值结果进行对比分析,并详细分析考虑泄漏的弹射过程中各热力学参数和弹道参数的变化规律。最后将考虑泄漏工况的理论计算结果与弹射试验数据及计算流体动力学(CFD)仿真结果对比,获得了相对真实的弹道参数。

1 问题描述

本文提出的双缸对称无杆式高压气动弹射器模型,其结构简图如图1所示。

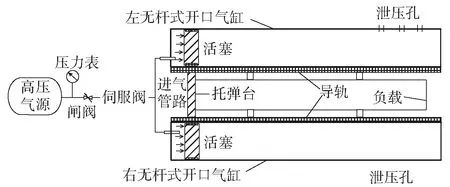
图1 双缸对称无杆式高压气动弹射器结构

该模型主要由高压气源(高压室)、左右对称分布的无杆式开口气缸(低压室)、托弹台、缓冲机构等部件组成,其中核心部件无杆式开口气缸如图2所示。将无杆式开口气缸呈双缸对称式分布,能显著降低偏心载荷,减小弹射摩擦力,能效利用率更高。

图2 无杆式开口气缸结构图

双缸对称无杆式高压气动弹射器的工作原理为:控制箱发出弹射指令后,阀控随即响应,控制阀门打开;高压气体经过进气管路流入气缸(低压室),当气体对活塞的作用力大于负载自重及摩擦阻力时,活塞带动动力输出臂、托弹台及负载一起运动;达到弹射行程后,两侧活塞组件撞击到对应的缓冲油缸组件,负载飞离托弹台,系统完成一次发射任务。

2 基于亥姆霍兹能的热力性质参数

2.1 干空气模型

以美国国家标准和技术局的标准空气模型为基准,其组成为氮气、氧气和氩气,各组成的体积百分比分别为78.12%、20.96%和0.92%。干空气的参考常数如表1所示。

表1 干空气的参考常数

2.2 干空气的状态方程

标准干空气的状态方程是基于现有实验下的压力p-密度ρ-温度T、热容、声速和气液平衡数据,使用最小二乘法拟合而来,该方程采用无量纲亥姆霍兹能的形式来表达:

(1)

式中:α(δ,τ)为无量纲的亥姆霍兹能,T为气体温度;a(ρ,T)表示亥姆霍兹能;R为空气理想气体常数;α0(δ,τ)为理想气体对亥姆霍兹能量的贡献部分(2.3节中简写为α0,上标0表示理想气体性质),δ=ρ/ρm表示约化密度,ρm表示最大冷凝密度,τ=Tm/T表示约化温度的倒数,Tm表示最大冷凝温度;αr(δ,τ)为对亥姆霍兹能量的剩余贡献部分(2.3节中简写为αr,上标r表示剩余性质);α0(δ,τ)、αr(δ,τ)的表达式分别如式(2)、式(3):

(2)

(3)

式中:系数N1～N19及ik、jk、lk的具体数值详见文献[7]。

2.3 热力性质参数计算

用于计算压缩因子Z、压力p、比热力学能u、比焓h的函数,可通过对亥姆霍兹能进行密度和温度的微分计算如下:

(4)

p=ZρRT

(5)

(6)

(7)

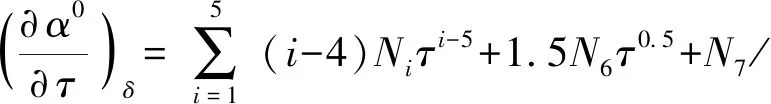
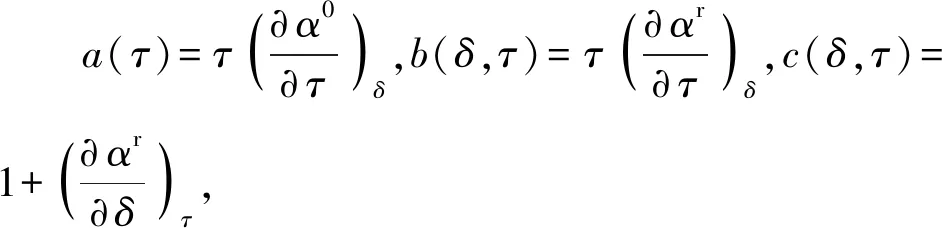
u=RT[a(τ)+b(δ,τ)]

(8)

h=RT[a(τ)+b(δ,τ)]+RTc(δ,τ)

(9)

3 无杆式开口气缸弹射器泄漏试验

无杆式开口气缸的开口结构特点决定了弹射器存在一定程度的泄漏,泄漏率与气缸内气体质量流量及缸内压力密切相关[19],直接影响到内弹道模型的预测精度。本文基于无杆式开口气缸弹射器开展泄漏试验,获得不同缸内压力和活塞行程下的泄漏率,并拟合出泄漏率与压力、行程的经验公式。

3.1 泄漏试验方案及步骤

如图3所示,泄漏试验系统由无杆式开口气缸、限位钢管、高压气源、空压机、干燥机、伺服阀、闸阀、安全阀、压力传感器、温度传感器和数据采集仪等组成。在活塞行程内取若干个固定位置,分别加载不同的缸内压力,保持阀门打开约10 s时间,以保证足够时间完成测试,测量并记录气源、缸内压力及温度等数据。高压气源容积约为2.5 m3,体积较大,导致不便对气源内部进行温度测量,因此假设高压气源温度为一恒定值,仅测量缸内温度变化。

图3 泄漏试验方案示意图

在泄漏试验中,由于活塞被限位钢管限制在一定位置,长时间保持高压有可能导致结构变形,为保证安全,泄漏试验只做了低压区域。考虑到无杆式开口气缸动密封结构的设计原理为缸内压力越高,密封处间隙越小,泄漏越小,因此低压下泄漏率要大于高压工况,低压试验下获得的泄漏率能反映整个泄漏率外包络。泄漏试验主要步骤为:

1) 通过不同长度的限位钢管,将活塞限制在不同行程l处(0 m、1.11 m、2.18 m、3.24 m、4.18 m、5.18 m);

2) 利用空压机向气源内充入高压空气;

3) 打开闸阀和伺服阀,使得高压空气进入开口气缸中(缸内最高压力p分别为1.77 MPa、2.76 MPa、3.76 MPa),并保持阀开10 s;

4) 通过数据采集系统,记录保持阀开过程中气源、气缸的压力时程曲线以及气缸的温度时程曲线;

5) 关闭阀门,释放高压气体。为使数据可靠,每组试验重复3次并取其平均值。

3.2 泄漏试验过程

开展泄漏试验,以缸内最高压力3.76 MPa、活塞行程2.18 m的工况为例说明泄漏试验过程,气源压力为4.2 MPa,在6 s时所有阀门打开,并保持10 s左右时间。试验过程中工质泄漏如图4所示。从图4中可见泄漏试验的直观过程:阀门打开后气缸即出现泄漏,泄漏处的高压气体形成白雾状,随着泄漏量的增大,气雾团也变大。保持阀开过程中,气源及开口缸内压力时程曲线如图5所示,开口缸内温度时程曲线如图6所示。

图4 工质泄漏过程

图5 压力时程曲线

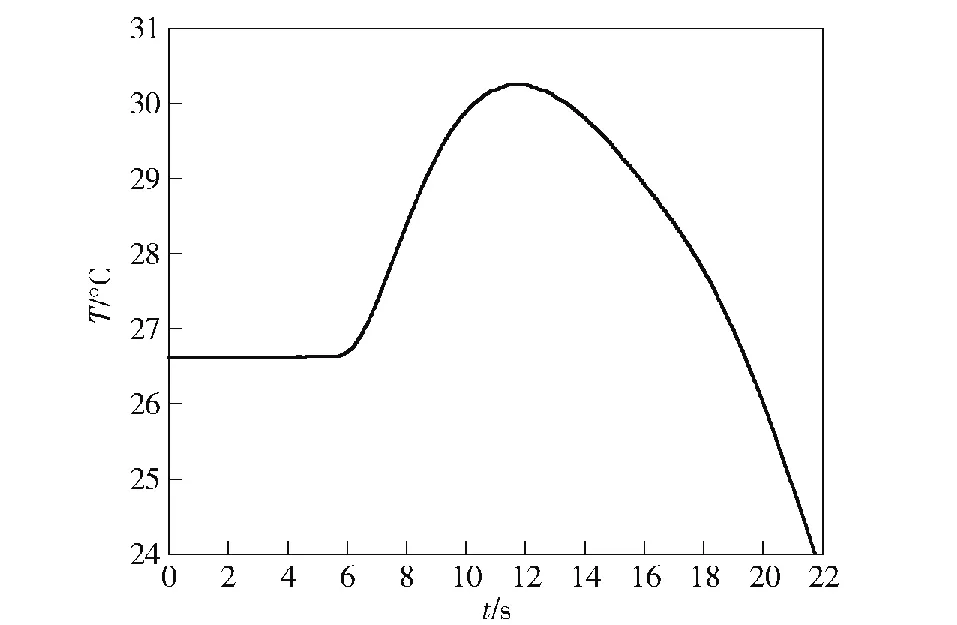
图6 温度时程曲线

从图5中可以看出,6 s后,高压气体迅速从气源进入气缸,气源压力在不到1 s内快速下降,相对应地,缸内压力迅速达到最高压力3.76 MPa,随后由于泄漏,缸内压力从峰值开始下降,气源压力也慢慢下降,从图6中可以看出缸内温度呈先上升后下降的变化趋势。

3.3 泄漏率计算方法及公式拟合

泄漏率的计算流程如下:

1) 根据图5、图6的压力与温度数据计算初始和最终时刻的气源及缸内工质密度;

2) 将得到的密度分别乘以体积,获得初始和最终时刻的气源及缸内工质总质量;

3) 两质量差值即为阀开过程中工质的泄漏量[20],再除以时间10 s,即可获得单位时间内的泄漏率。

工质密度的两种计算方式如下:

1) 将高压气体视为理想气体,使用密度换算公式计算理想密度,如式(10)所示;

2) 将高压气体作为真实气体,根据式(11)计算出真实密度。

(10)

(11)

式中:ρa=1.293 kg/m3;pa为标准大气压力。

分别使用上述两种方法,得出不同缸内压力p及活塞行程l下弹射装置的泄漏率η,如表2所示。

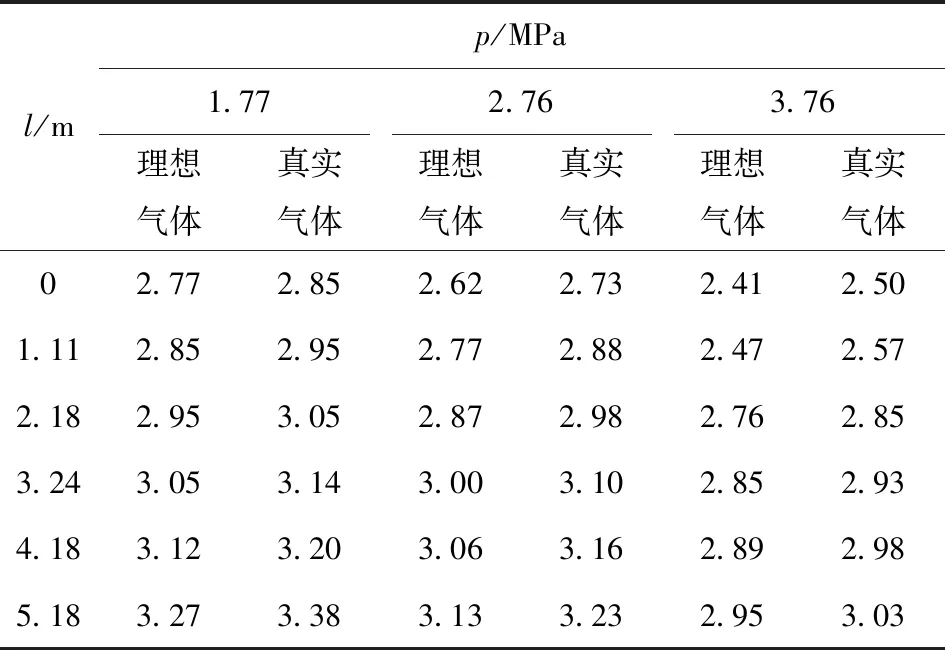
表2 两种计算方式下的泄漏率

从表2中可以看出以下规律:

1) 两种计算方法下,泄漏率均随着行程增加而增大,随缸内压力增大而减小;

2) 理想气体假设下的泄漏率整体比真实气体假设下的值小,经计算,理想气体假设下泄漏率比真实气体假设下泄漏率偏小的百分比最大约为4%;

3) 真实气体假设下,泄漏率最小为2.5%/s,最大为3.38%/s,整体不超过4%/s。

对于规律1),可以从开口气缸的密封结构特点角度解释:行程越长,密封面越长,泄漏间隙长度也越长,从间隙处泄漏的气体质量越大,故泄漏率随之增大;缸内压力越大,密封面处贴合越紧密,泄漏间隙越小,从间隙处泄漏的气体质量越小,故泄漏率随之减小。

根据规律2)可知,真实气体假设下得到的泄漏率更为精确,根据这组数据,采用最小二乘法拟合出泄漏率η与压力p、行程l的关系式为

η=3.188×10-2-1.808×10-3p+9.710×10-4l-8.763×10-8pl+1.700×10-5p2+1.784×10-6l2

(12)

4 无杆式高压气动弹射器内弹道模型

为简化问题,做如下假设:

1) 工作过程时间短,假设系统绝热;

2) 忽略气体动能、势能及气体黏性;

3) 不考虑两侧气缸的压力不平衡因素;

4) 活塞达到推弹行程时,进气腔与泄气孔相通,气体及时泄出,忽略剩余气体对缓冲过程的影响。

4.1 伺服阀控制方程

弹射过程中通过阀门喷口的气体有亚声速和声速两种流动情况,喷口流量方程为

(13)

式中:ph为高压室气体压力;Th为高压室气体温度;pl为低压室气体压力;μx为流量修正系数;A为阀开口截面积;γ为空气绝热系数。

阀门开启规律对于内弹道控制有重要的影响,且与阀的开关原理及阀内结构直接相关,阀控系统直接控制阀芯运动及阀门的开启。将阀门开口截面积A表示为阀芯位移d的连续函数,再通过位移传感器测量并拟合出阀芯位移d-t函数,即可得出开口截面积A随时间变化的连续函数。

为便于与下文弹射试验结果对比,根据试验所用阀的原理及结构,画出阀的简图如图7所示,得到阀的开口截面积A与阀芯位移d、阀门管道半径r、辅助计算夹角θ的关系式如式(14)、式(15)所示。

图7 气阀简图

(14)

(15)

从式(15)中可以看出,开阀面积A是根据阀门管道半径r及阀芯位移d计算得出的,最大开阀面积Amax与管径r及阀芯最大位移值dmax均为正相关关系,阀门管道半径r及阀芯最大位移值dmax通过影响最大开阀面积Amax进而对弹射内弹道产生影响。

4.2 高压室控制方程

质量方程为

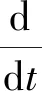
(16)

式中:ρh为高压室气体密度;Vh为高压室体积。

能量方程为

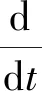
(17)

式中:uh和hh分别为高压室的比热力学能和比焓。

4.3 低压室控制方程

质量方程为

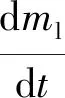
(18)

能量方程为

(19)

式中:ml为流入低压室的气体质量;ul为低压室的比热力学能;n为开口气缸数目;S为活塞推力面积。

活塞运动方程为

(20)

式中:v为弹射速度;me为弹射质量;g为重力加速度;α为发射角。

(21)

式中:V0为低压室初始体积。

5 弹射内弹道结果分析

5.1 数学模型求解与结果分析

根据第4节中推导的考虑泄漏、真实气体效应及真实开阀规律的精确内弹道数学模型,分别对考虑泄漏和不考虑泄漏两种工况,在MATLAB 2014a软件环境下,采用4阶龙格-库塔法编制数值程序,对微分方程组进行求解。计算所需参数及自变量初始值如表3和表4所示。

表3 模型中的相关参数

表4 自变量的初始值

图8～图12分别为考虑和不考虑泄漏的弹射过程中高低压室的温度变化、高低压室的压力变化、负载运动学参数变化及从高压室到低压室的质量流量变化曲线。从图8～图12中可以看出,考虑泄漏的弹射过程中高低压室的温度、高低压室的压力、负载运动学参数等曲线的数据均比不考虑泄漏的弹射过程中相关曲线的数据小;而考虑泄漏的弹射过程中从高压室到低压室的质量流量变化曲线的数据比不考虑泄漏的弹射过程中相关曲线的数据大。

图8 高、低压室温度曲线

图9 高压室压力曲线

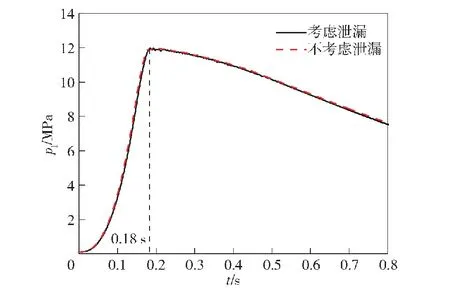
图10 低压室压力曲线

图11 负载运动学参数变化曲线

图12 从高压室到低压室质量流量曲线

上述规律恰好体现了泄漏对弹射过程的内弹道有一定的影响:与没有泄漏的工况相比,由于泄漏的存在,使得低压室的压力和温度更低,推动负载运动所需的气体质量更大,使得从高压室流向低压室的气体质量流量也更大,造成高压室的压力及温度下降得更快,最后反映到负载的运动上表现为相同时间内负载的过载更低,速度及位移更小。这样就回到了分析的开始,分析过程自洽。

图13给出了考虑泄漏弹射过程中泄漏率η的变化曲线。从图13中可以看出,整个弹射过程中泄漏率在0.18 s之前呈现变小趋势,在0.18 s以后慢慢变大。

图13 泄漏的质量流量曲线

结合图11(a)及图10可知,在0.18 s之前位移几乎为0 m而低压室压力迅速增至最大值,在0.18 s之后位移开始增大而低压室压力呈下降趋势。因此在0.18 s之前,泄漏率式(12)中-1.808×10-3p一项起主要作用,泄漏率减小;在0.18 s之后泄漏率式(12)中9.710×10-4l一项其主要作用,泄漏率慢慢增大,与3.3节中从开口气缸的密封结构特点上解释规律1)的内容相呼应。

5.2 考虑泄漏的弹射内弹道结果分析

图14和图15给出了阀芯位移及开阀面积的变化曲线。为便于分析,图16中给出了考虑泄漏的弹射过程中高、低压室及二者压差的压力变化曲线。

图14 阀芯位移曲线

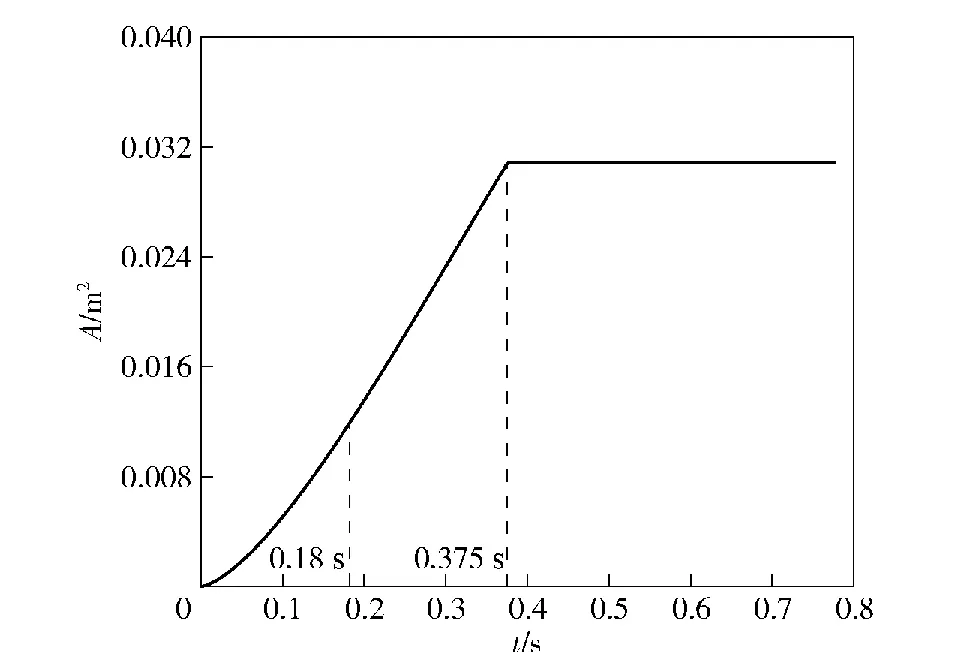
图15 开阀面积A曲线

图16 考虑泄漏的高、低压室压力曲线

由图14可看出,阀门最大行程150 mm,阀门开启动作响应时间0.375 s。由图15可以看出,随着阀门开启,开阀面积A随时间的变化率逐渐增大,0.18 s 之后开阀面积A近似线性增大,直至0.375 s阀门达到最大行程,开阀面积A达到最大值 0.030 8 m2,此时阀门完全开启。

图8(a)和图8(b)曲线为考虑泄漏的弹射过程中高、低压室的温度变化曲线,所示温度变化可分为3个时间段分析:

1) 0～0.18 s。在这个阶段,随着阀门的开启,高压室气体不断向低压室流动,高压室温度迅速降低,低压室温度迅速升高。分析原因可知在 0.18 s 之前高压室和低压室的压差很大(见图16),高压室内气体以较大的质量流量冲入低压室,使得高压室气体能量迅速降低,低压室气体的能量迅速升高。

2) 0.18～0.375 s。在这个阶段,高压室和低压室的压差很小,虽然开阀面积仍在增大,但此时随着负载开始加速,低压室容积逐渐增大,进而能量消耗逐渐加快。因此,低压室温度呈现下降趋势,同时高压室温度继续下降,下降速度比上一个阶段小。

3) 0.375～0.777 s。在这个阶段,开阀面积已经达到最大值,但此时负载速度及位移快速增大,能量消耗进一步加快。此时,高压室温度的下降速度比第2个阶段大,同时低压室温度继续下降。

联系图11(a)、图12、图15、图16进行相互比照,将质量流量及压力变化曲线分为4个时间段进行分析:

1) 0～0.15 s。高压室初始压力约为 13.2 MPa,高、低压室的压差很大(见图16),在这个阶段,高压室流入低压室的气体质量流量快速增大,并在0.15 s左右达到最大值(见图12)。同时,随着阀门的开启,开阀面积A逐渐变大(见图15),高压室气体通过发射阀快速进入低压室,导致高压室压力持续降低,低压室压力快速升高。

2) 0.15～0.18 s。在这个阶段,虽然开阀面积A仍在增大,但高、低压室的压差相对变小(见图16),式(13)中(pl/ph)2/γ-(pl/ph)(γ+1)/γ的值及高压室压力持续变小,此时质量流量出现下降趋势,联系图11(a)在0.18 s之前位移几乎为0 m,因此低压室压力仍持续增大,同时高压室压力持续降低,二者在0.18 s左右达到数值十分接近的状态。

3) 0.18～0.375 s。在这个阶段,虽然高低压室的压差很小(见图16),但开阀面积A近似线性增大,式(13)中开阀面积A起主导作用,因此质量流量开始慢慢增大,在这个过程中高、低压室压力以及质量流量曲线均出现小幅波动,对此现象分析如下:

此时负载在低压室推力的作用下慢慢运动(见图11(a)),随着质量流量增大,高压室压力减小低压室压力随之增大,然而由于负载的运动,使得低压室容积也增大,最后导致低压室压力降低,式(13)中(pl/ph)2/γ-(pl/ph)(γ+1)/γ的值随之降低,使得质量流量开始变小,但是由于开阀面积A一直增大,使得质量流量又继续增大,又回到分析的开始,如此反复数个周期。在这个阶段低压室容积增大部分的气体量大于高压室流入低压室的气体量,因此高、低压室压力均以几乎相同的速率持续下降。

4) 0.375～0.777 s。在这个阶段,发射阀全部打开,开阀面积A不再变化,在阶段初期高、低压室的压差几乎为0 MPa(见图16),但随着负载的加速运动,低压室容积加速增大,低压室容积增大部分的气体量远大于高压室流入低压室的气体量,因此高、低压室压力均持续下降,且低压室压力下降速率大于高压室,高、低压室的压差慢慢增大,式(13)中(pl/ph)2/γ-(pl/ph)(γ+1)/γ的值慢慢增大,质量流量也增大。

由图11(a)中的实线可以看出,在0.086 s以前,由于活塞底部气体推力未能克服负载重力以及静摩擦力,弹体处于静止状态;从0.086 s起,活塞开始带动托弹台及负载加速运动,并在约9.6 m的弹射行程内加速至27.2 m/s(见图11(b)的实线)。从图11(b)中的实线可以看出:在0.15 s之前,负载速度很小;在0.15 s之后负载速度开始迅速增大,其随时间的变化规律基本趋近于线性变化。联系 图(16)及图11(c)中的实线可看出,弹射过程中负载过载系数的变化趋势与低压室压力一致,原因也一致,在此不赘述。

5.3 理论仿真结果与试验数据对比

基于双缸对称无杆式气动弹射器原理样机,搭建图17所示弹射试验测试系统进行弹射试验,图18 给出了某次弹射试验的现场截图。

图18 弹射试验现场截图

为验证理论模型的有效性,试验测量了阀芯位移曲线、气源与两侧开口气缸内压力变化曲线、过载曲线以及达到弹射最大行程时刻的速度值。

试验环境温度300 K,阀芯位移传感器选用量程400 mm的日本Panasonic激光位移传感器,非线性度小于±0.1%F.S.,压力传感器选用量程为 25 MPa 的瑞士Kistler传感器,精度等级为0.5%F.S.,加速度传感器选用中国工程物理研究院研制的无线三轴线加速度测量系统CBQ001,量程±100g,自带电源及存储功能。

限于试验条件,无法直接测得负载的速度变化曲线,采用一组相隔Δs距离的光电开光安装于弹射最大行程处(见图17),当活塞经过一组光电开光后,采集系统分别采集到不同的光电信号,根据Δs及光电信号之间的时间差Δt,即可间接获得该间距Δs范围内的平均速度,即弹射最大行程时刻的速度。根据试验中测得的负载加速度时间曲线,对其进行积分,得到速度-时间曲线,再对速度-时间曲线进行积分,得到位移-时间曲线。将试验的测试结果与理论仿真结果进行对比,如图19～图21所示。

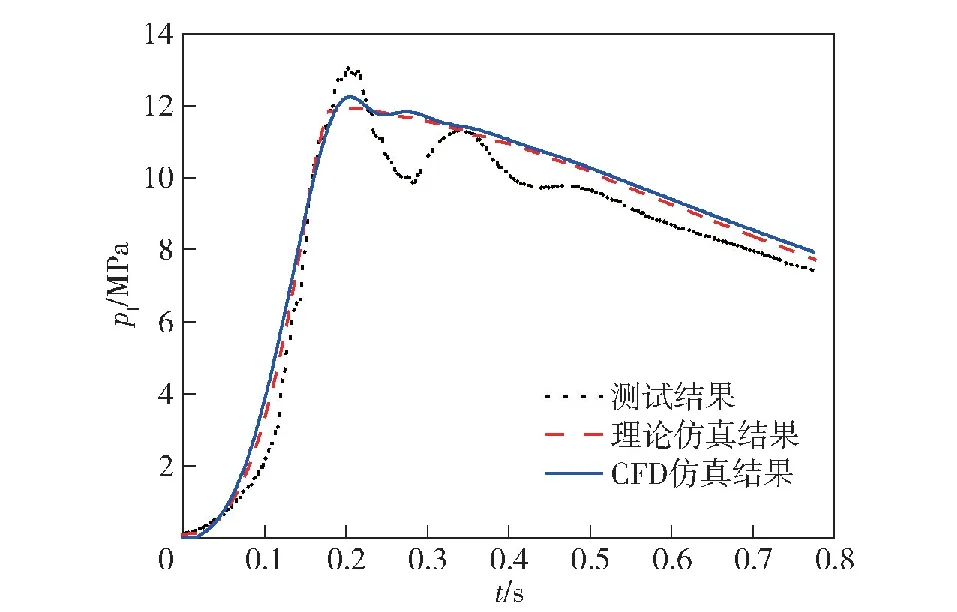
图19 低压室压力曲线

图20 高压室压力曲线

图21 负载运动学参数变化曲线

通过光电开关数据计算出弹射末速度27.5 m/s,与仿真计算值接近。从图19～图21中可看出,高、低压室的压力及过载的测试结果在弹射前期及后期与仿真结果一致性很好,在0.15～0.5 s左右均出现一定程度的波动,且基本在仿真结果附近的范围波动。

经过分析,认为出现波动的原因如下:在弹射中期,低压室处于初始建压完成状态,此时开口气缸内高压气体的流场状态不稳定;此外,负载也刚开始低速运动,不稳定的压力、导轨处复合摩擦状态[21]等多种因素使得负载的运动呈现“卡顿”的状态,表现在曲线上即出现波动。在弹射后期,开口气缸内流场稳定,导轨处润滑良好,负载速度越来越大,运动逐渐趋于稳定,曲线也不再波动。

5.4 CFD仿真结果与试验数据对比

5.3节分析了高、低压室压力及过载的测试结果在0.15～0.50 s左右出现波动的可能原因,其中导轨处复合摩擦状态这一现实因素在仿真计算中很难涉及,在此仅对不稳定流场状态因素进行进一步的研究。

由于根据内弹道方程组求解的零维内弹道是基于“零维假设”,即不考虑高、低压室压力沿空间的分布,只考虑其随时间的变化规律,同时也不考虑气体在低压室内的流动,因此该结果不能捕捉到多维时空特性场的规律,使得理论计算曲线与试验曲线有一定的差异性。在此,基于计算流体力学方法,对双缸对称无杆式高压气动弹射器的弹射过程进行数值模拟(为简化模型不考虑弹射过程中的泄漏),并将仿真结果与试验数据进行对比。

双缸对称无杆式高压气动弹射器包括高压气源(高压室)、左右对称分布的无杆式开口气缸(低压室)、阀控及管路等如图1所示,数值模型中将伺服阀简化为垂直于管路的方块。网格模型如图22所示,采用六面体网格,阀门右侧的网格作加密处理。

图22 网格模型示意图

基于压力求解方法对弹射过程气体流动规律进行求解,初始时刻高压室赋压力值为13.2 MPa,控制方块按照图14所示阀芯的运动规律模拟实际阀门的开启过程,其与管路两侧采用交界面实现流场参数的传递,活塞的运动通过在气缸轴向设置6自由度实现,动网格采用层动模式,其余边界均为壁面边界条件。

图19～图21给出了CFD仿真结果与试验数据的对比曲线,其中高、低压室压力曲线均为体积平均压力。图23给出了0.375 s时刻的压力云图。

图23 0.375 s时刻的压力云图

从图19～图21的曲线对比中可以看出,CFD仿真结果较好地捕捉到了多维时空特性场,其中高、低压室的压力及过载曲线也在0.15～0.5 s左右出现一定程度的波动,虽然与试验数据相比仍有一定的差异,但与理论仿真结果具有良好的一致性。考虑到实际试验过程中的复杂因素无法一一复现,在此认为仿真计算结果均与试验结果总体基本一致,验证了弹射原理及弹射过程内弹道模型的正确性。

6 结论

1) 两种计算方式下泄漏率均随着行程增加而增大,随缸内压力增大而减小;理想气体假设下计算的泄漏率整体比真实气体假设下的值小,偏小的百分比最大为4%;真实气体假设下,泄漏率最小为2.5%/s,最大为3.38%/s,整体不超过4%/s。

2) 基于NIST发布的由实验数据拟合的标准干空气热力学状态方程,以真实热力学参数为理论基础,构建了考虑动态泄漏、真实气体效应及真实开阀规律的精确内弹道模型,并分别对考虑泄漏和不考虑泄漏两种工况进行数值求解。

3) 对两种工况下数值结果进行对比分析,结果表明泄漏对弹射过程的内弹道有一定的影响,最后反映到负载的运动上表现为相同时间内负载的过载更低,速度及位移更小。给出了考虑泄漏的弹射过程中,高压室放气、低压室充气的详细动态热力学过程及弹道性能的详细分析。

4) 进行弹射试验,将考虑动态泄漏的仿真计算与试验结果相比较:高、低压室的压力及过载的测试结果在弹射前期及后期与仿真结果的一致性很好,在弹射中期均出现一定的波动,但基本在仿真结果附近的范围波动。

5) CFD仿真结果较好地捕捉到了多维时空特性场,其中高、低压室的压力及过载曲线也在弹射中期出现一定的波动,虽然与试验数据相比仍有一定的差异,但与理论仿真结果具有良好的一致性。