水下爆炸载荷下金字塔夹芯板抗冲击性能及破坏模式研究

李富荣, 荣吉利, 王玺, 陈子超, 韦振乾, 赵自通

(1.北京理工大学 宇航学院, 北京 100081; 2.北京航天发射技术研究所, 北京 100076)

0 引言

随着世界科技和军事的发展,出现了越来越多高精度、高杀伤力的水下攻击武器,对水面及水下舰艇的生存能力提出了更大的考验。水下爆炸是对海上舰艇产生威胁的主要攻击方式之一,研究水下爆炸对不同材料和结构的冲击及毁伤模式,对于提升舰船的抗爆抗冲击性能有一定的意义。

夹芯结构具有质量轻、抗冲击能力强的特点,对于不同的夹芯结构,各国科研人员针对其在水下爆炸冲击方面的响应开展了大量的研究。Xue等[1]对3种夹芯板进行了研究,发现3种夹芯板的抗冲击性能都优于相同质量的实心板,同时由于流体-固体耦合(简称流-固耦合)的作用,夹芯板可以降低冲击波传递的冲量。Wei等[2]、Dharmasena等[3-4]通过药式水下爆炸加载装置,对多层金字塔点阵、六边形蜂窝、四边形蜂窝、多层波纹结构进行了冲击实验,结果表明蜂窝芯层在准静态加载下具有最高的屈服强度。Fan等[5]利用药式设备对蜂窝夹芯板进行实验,研究了不同面板厚度及芯层密度对夹芯板失效模式的影响。Zhou等[6]对PVC夹芯板进行了水下爆炸实验,研究了不同配置参数对夹芯板性能的影响。Deshpande等[7]在Taylor一维应力波的基础上研究了非药式水下爆炸加载装置。国内项大林等[8-9]研发了国内首套非药式水下爆炸冲击加载装置,并指出活塞厚度是决定压力衰减时间的因素。任鹏等[10-11]对船用加筋板和波纹夹层板进行了冲击实验,得到了动态响应特性。姚熊亮等[12]采用有限元计算程序Abaqus对舰船水下爆炸进行了数值模拟。He等[13]对船体结构进行了水下爆炸实验,并利用Autodyn软件进行了流-固仿真,仿真结果与实验吻合良好。韦辉阳等[14]利用非药式水下爆炸加载装置结合Abaqus仿真,对带有预制缺陷的实心板进行了动态响应分析,发现靶板在破坏时倾向于产生尽可能少的裂纹的同时将能量释放出去。魏子涵等[15]利用水池爆炸实验研究了蜂窝夹层结构的爆炸特性,并利用仿真结合优化算法进行了优化设计。苏标等[16]对双层加筋板进行了接触式水下爆炸实验,结果表明不同爆距下的板架损伤模式不同。代利辉等[17]结合理论及仿真,对固支方板在水下冲击下的动态响应进行了分析。Cui等[18]对四面体金属夹芯结构在空气中进行了爆炸实验并与相同密度的蜂窝夹芯结构进行了比较,发现四面体夹芯板具有更好的抗冲击性能。泮世东等[19]根据理论推导,对金字塔夹芯结构进行优化,提高了其等效剪切强度。Xue等[20]用SPH-FEM耦合方法,研究了背板厚度对金字塔夹芯板的抗冲击性能影响。 Feng等[21]在金字塔夹芯板的基础上,设计了一种沙漏型点阵结构并进行实验,研究结果表明具有该种结构的夹芯板相较于金字塔夹芯板有更强的抗撕裂性能。

对于金字塔点阵夹芯结构,已有研究大部分集中于空气中爆炸和准静态压缩,而由于水下爆炸存在明显的流-固耦合现象,金字塔夹芯板在水中冲击下的失效模式以及影响其抗冲击性能的参数仍待明确。本文利用等效水下爆炸冲击加载实验装置对不同参数的金字塔夹芯板进行冲击实验,并结合流-固耦合仿真进行分析,得到了金字塔夹芯板在不同载荷下的破坏模式及芯层吸能特点。

1 等效水下爆炸冲击实验

1.1 实验设备及原理

实验利用等效水下爆炸冲击加载实验装置进行,其示意图如图1所示。

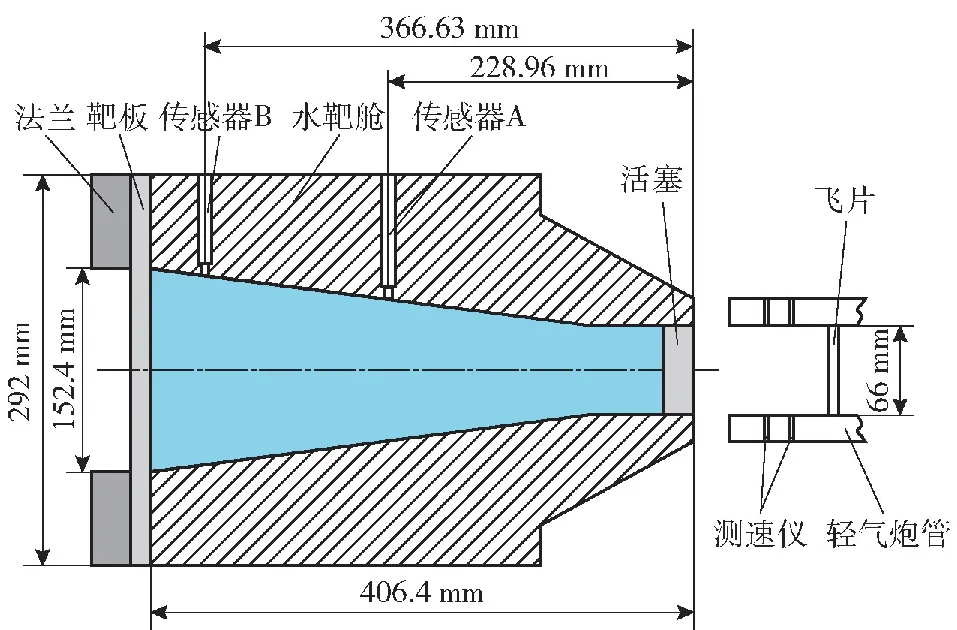
图1 等效水下爆炸冲击加载装置

利用轻气炮作为动力源,在5 m长的炮管内对飞片进行加速,根据气室内压力的大小,可对飞片施加50～400 m/s的速度,其速度可由炮管出口处的测速仪进行测量。飞片经由炮管飞出撞击在水靶舱舱口的活塞上,在活塞内产生应力波,根据一维应力波理论,应力波在活塞内经过多次透射与反射,从与水接触的一端传出,假设传播过程中无能量耗散,其压力可简化为

ppoint=pm·e-t/θ

(1)

式中:ppoint为测点处的压力;pm为测点处最大压力值,

(2)

D0为水靶舱入口处的直径,D为测点处的直径,ρ0为材料密度,C0为材料中的声速,(ρ0C0)1和(ρ0C0)2分别为活塞和水的波阻抗,v1为撞击前飞片的速度;θ为时间衰减常数,

(3)

L2为活塞的厚度。式(1)与水下爆炸冲击波的经验公式一致,表明该设备可以用于模拟水下爆炸冲击实验。

1.2 实验靶板

利用等效水下爆炸冲击加载实验装置对金字塔点阵夹芯结构进行实验,实验所用金字塔夹芯板如图2所示,夹芯板通过12个螺栓固定在水靶舱上,夹芯板直径292 mm,受载区域直径152.4 mm。其中与水接触的一侧面板称为前面板,与空气接触的一侧称为后面板。夹芯板芯层为金字塔点阵结构,其生产方式为利用线切割将所需厚度铝板切割成连续的波纹状金属条,再通过预留的凹槽采用嵌锁的方式将若干组金属条拼接,形成金字塔点阵芯层,并用胶结方式进行加固。金字塔杆件截面边长为 1 mm,芯层厚度为15 mm(后简称芯层A)的金字塔杆件线切割示意图如图3所示。

图2 金字塔夹芯板

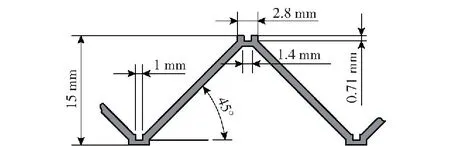
图3 线切割示意图

1.3 仿真模型

利用有限元软件Abaqus进行有限元仿真,建立图1所示的全尺寸流-固耦合仿真模型,约束条件与实验一致,其仿真模型如图4所示。

图4 有限元仿真模型

建立欧拉域,并将水靶舱内部欧拉域用水填充,欧拉网格总数为43万,水用如下状态方程进行描述:

(4)

式中:p为压力;C为us-up曲线上的截距(us与up为物质冲击速度与粒子速度);S为us-up曲线斜率系数;μ=ρw/ρ0-1,ρw为水的密度,ρ0为水的初始密度。相应的参数如表1所示。

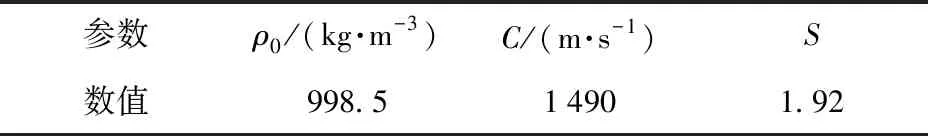
表1 水的状态方程参数

建立夹芯靶板的实体仿真模型,靶板芯层采用C3D8R减缩积分单元,网格尺寸0.5 mm,金字塔杆件横截面边长方向两个网格,金字塔芯层单胞网格示意如图5所示。面板采用壳建模,厚度方向5个积分点,网格类型S4R,网格尺寸1 mm。整个靶板网格数量24万。

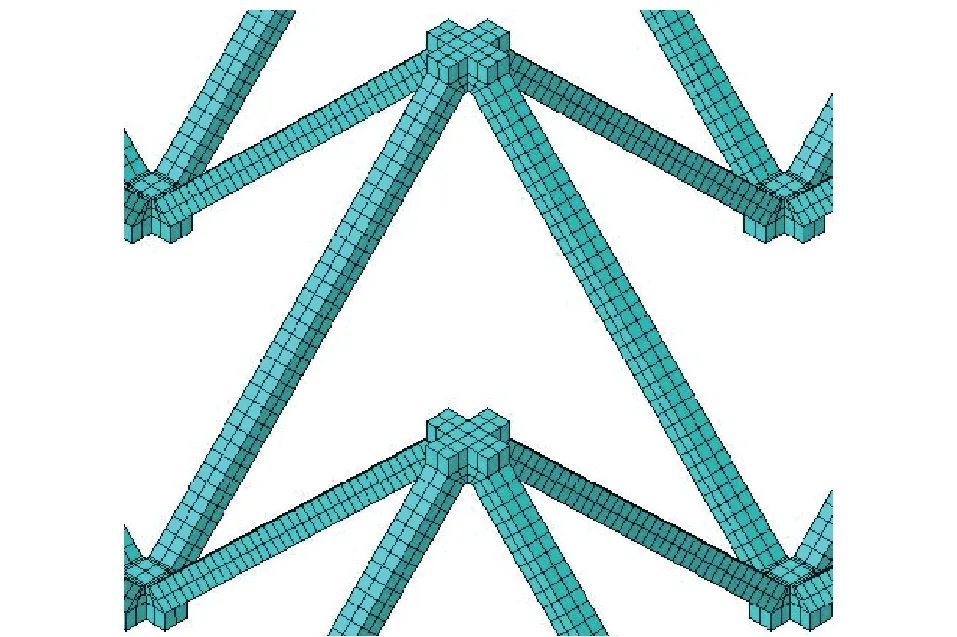
图5 芯层网格示意图

芯层与靶板前后面板为tie接触,靶板前面板与水靶舱接触处和后面板与法兰接触处在12个螺栓对应位置设置tie接触,以模拟螺栓固定条件。夹芯靶板的有限元透视模型如图6所示。

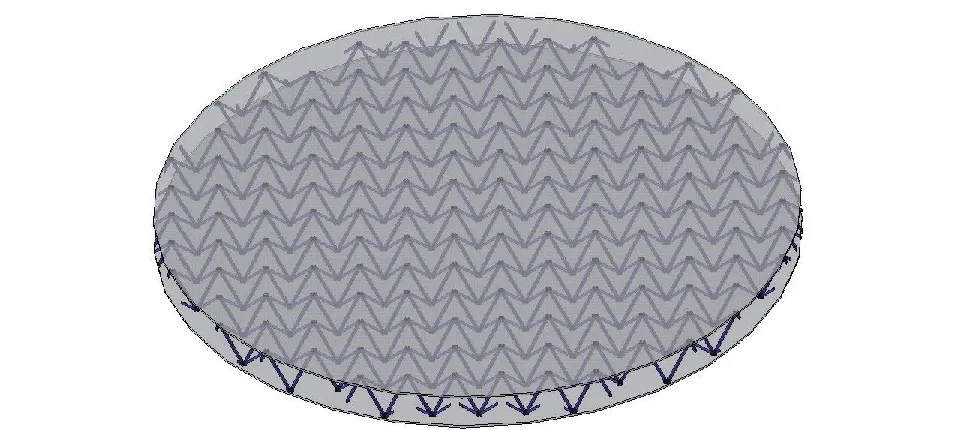
图6 金字塔夹芯板有限元模型

靶板材料为铝合金6061-T6,密度2 800 kg/m3,弹性模量68.9 GPa,泊松比0.33,其本构方程通过Johnson-Cook本构来描述:

(5)

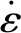
表2 6061-T6 Johnson-Cook参数

2 金字塔夹芯板动态响应

2.1 实验及仿真结果对比

利用等效水下爆炸冲击加载装置对不同几何参数芯层的金字塔夹芯板开展等效水下爆炸冲击实验,选取飞片与活塞相撞时为正碰的实验结果进行分析,提取水靶舱内传感器A、B两处的压力,并用两台高速相机利用3D-DIC技术获取夹芯靶板后面板的实时离面位移。对实验进行有限元仿真,设置与实验条件一致的飞片厚度、速度以及靶板几何参数,对比仿真结果与实验结果。

当飞片厚度为8 mm、速度为v=113.07 m/s时,利用式(2)和式(3)可求出靶板处的峰值压力与衰减系数。设W为装药量(kg),R为爆距(m),若利用球型TNT水下爆炸的经验公式

(6)

(7)

对其进行对比,则可知实验中的等效水下爆炸冲击波,可近似为1.83 kg的球型TNT爆炸时对距爆心2.142 m处的目标产生的冲击波。

A、B两测点处的压力时程曲线实验与仿真结果如图7所示。测点处的峰值压力大小及误差如表3所示。由图7及表3可知,通过实验获得的压力时程曲线与通过仿真获得的压力时程曲线峰值大小以及衰减情况基本一致,误差符合预期要求,验证了建立的有限元仿真模型的有效性,以便于利用仿真对不同参数的金字塔夹芯板在水下爆炸载荷下的破坏模式进行研究。

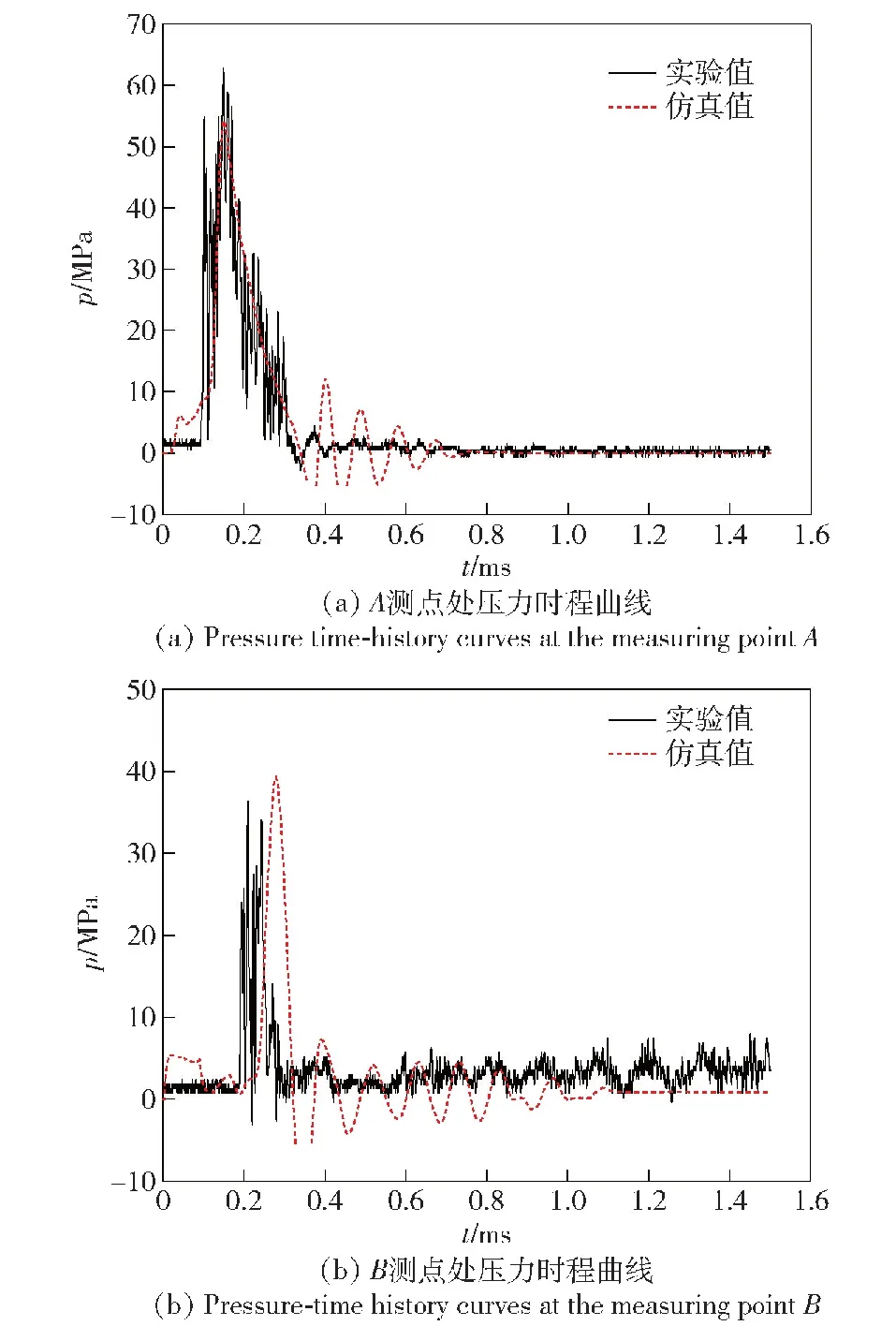
图7 A、B测点实验值与仿真值对比

对金字塔芯层的网格收敛性进行分析,分别对芯层划分0.50 mm、0.35 mm和0.25 mm的网格并进行仿真,0.50 mm网格在芯层杆件横截面边长方向为2层网格,0.35 mm网格在芯层杆件横截面边长方向为3层网格,0.25 mm网格在芯层杆件横截面边长方向为4层网格,最终得到的后面板中心点离面位移以及仿真花费时间如表4所示。

表4 不同网格下后面板变形及运算时间对比

由表4可以发现,0.5 mm网格的计算结果与更小的尺寸网格的计算结果误差在可接受范围内,但运算时间大幅缩短,表明0.5 mm网格可以达到所需的计算精度。在后续的仿真中,将采取0.5 mm网格进行计算。

通过仿真得到的后面板离面位移w和3D-DIC系统采集到的夹芯板后面板离面位移如图8所示。

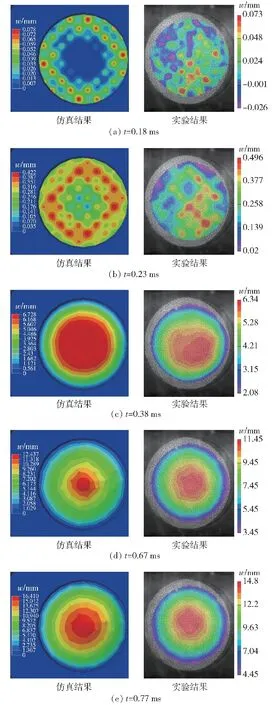
图8 不同时刻后面板变形情况

由图8可见,3D-DIC无法对散斑边缘进行数据处理,实验得到的离面位移云图不包含与法兰接触的圆形区域。由于飞片撞击活塞不是理想条件下的正碰以及夹芯板在加工时具有的瑕疵,夹芯板的变形并不像仿真中一样规则且对称,但仍然可以观察到夹芯板后面板离面位移的仿真值与实验值基本一致,进一步证明了仿真模型的有效性。

对后面板变形过程进行分析,夹芯板的响应最先出现在边缘,之后逐渐向中心集中,后面板与金字塔芯层连接处有更大的塑性变形,会出现明显的点状凸起,同时这些位置也会发生应力集中,受更大载荷时,这些位置可能会产生更大的凸起并产生裂纹,导致面板在这些位置发生撕裂。

后面板中心点的位移时程曲线如图9所示,从中可见由仿真得到的后面板中心点位移时程曲线与实验得到的位移时程曲线在0.5 ms前斜率基本相同,0.5～0.7 ms仿真得到的后面板中心点位移减小,与实验值产生了较大误差,这是因为实验中芯层与后面板非理想绑定条件,发生了脱胶现象,导致芯层压缩时后面板未发生明显回弹,而仿真中后面板发生了回弹,在芯层压实后后面板又获得较大速度,位移增大。最终结果表明,后面板中心点离面位移仿真值与实验值最终趋于一致,表明该仿真模型可以很好地模拟实验条件。

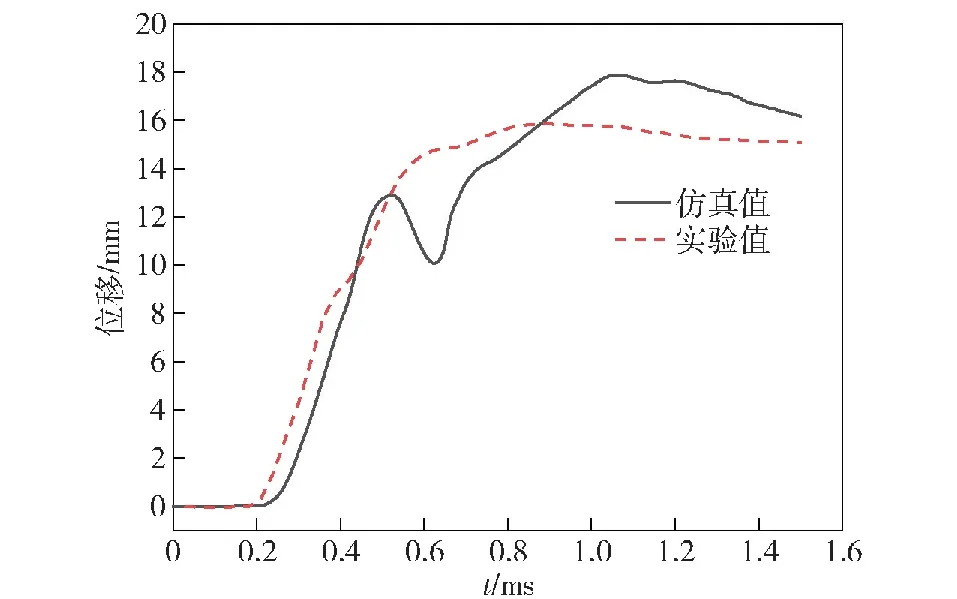
图9 后面板中心点位移

2.2 结果分析

利用仿真得到夹芯板前、后面板中心点位移、靶板中心点芯层压缩量时程曲线,以及塑性应变能时程曲线,如图10、图11所示。

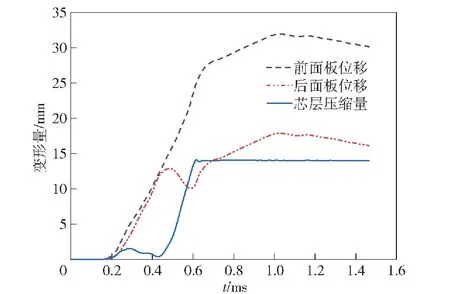
图10 夹芯板变形时程曲线

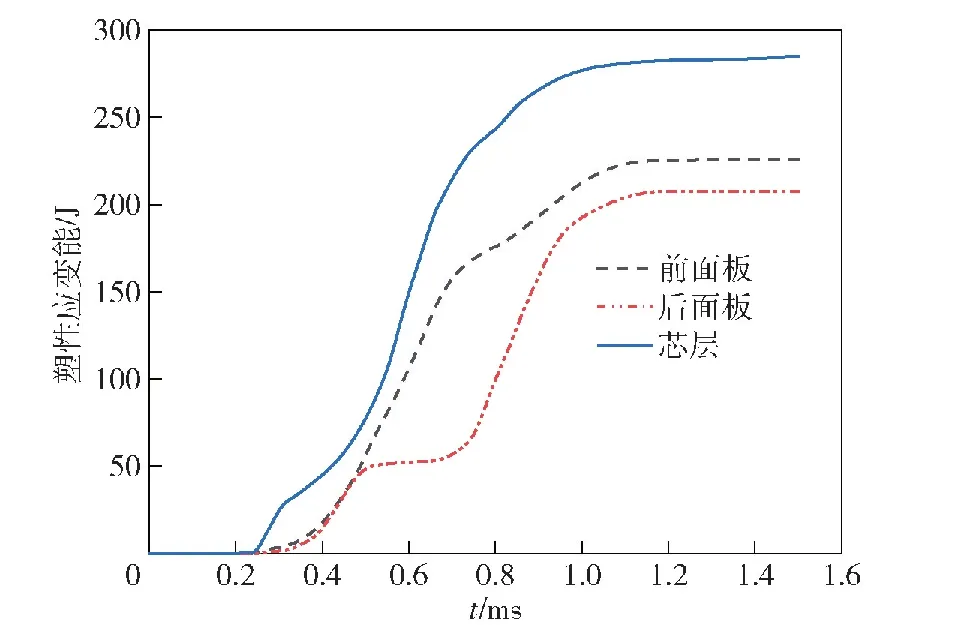
图11 夹芯板塑性应变能时程曲线

金字塔夹芯板的变形可以分为以下3个阶段:第一阶段为:0.2 ms时等效水下爆炸冲击波传递至夹芯板并使其开始变形,在0.43 ms前,主要发生的是靶板的整体变形,前后面板同步变形,芯层压缩量较小,芯层变形模式为整体的弯曲变形;第二阶段为:0.43～0.62 ms时间内,大部分芯层被压缩变形,芯层塑性变性能曲线在该阶段斜率最大,后面板变形趋势减弱并发生回弹,后面板塑性变形能斜率减小;第三阶段为:0.62 ms后,靶板中心点位置芯层压实,而芯层其他位置尚未压实,仍在发生塑性变形,已经压实位置的前面板将速度重新传递至后面板,后面板变形量开始增大,其塑性应变能斜率在该阶段达到最大,1 ms后夹芯板不再发生塑性变形,前后面板变形量略微减小,弹性变形部分恢复。

金字塔夹芯板受水下爆炸冲击后,其整体变形情况如图12所示,左图为仿真得到的最终变形结果,右图为实验结果。由图12可见,夹芯靶板受载区域内产生半球形变形,中心变形最大,固定区域几乎未发生变形,靶板受载区域边缘产生明显折痕,靶板面板上出现十字形凸起,为芯层压缩时挤压面板所致。图12中红色圆圈处表示靶板受冲击时产生径向载荷,而由于四周存在螺栓固定,靶板无法向中心收缩,并且由于芯层不是连续的实体,从而导致面板出现了褶皱。

图12 金字塔夹芯板变形情况(左为仿真结果,右为实验结果)

金字塔芯层的破坏模式如图13所示,由于夹芯板加工存在误差,实验结果的芯层破坏并不像仿真一样规则,但芯层的破坏模式基本相同:金字塔芯层的杆件发生屈曲变形,芯层整体压缩为扁平状;在靠近固定边界处的金字塔单胞顶部和中心处的金字塔单胞顶部发生了断裂。

图13 金字塔芯层破坏模式(上为实验结果,下为仿真结果)

金字塔芯层质量34.5 g,前后面板均为188 g,其等效密度(芯层质量/等体积下芯层材料的质量×100%)仅为1.22%,芯层质量为单个面板质量的18.4%。由图11可知:芯层塑性应变能为284.7 J,是前面板塑性应变能的126.3%,单位质量芯层吸能是单位质量面板吸能的6.86倍以上。将金字塔夹芯板与相同质量的实心铝板进行比较,实心铝板厚2.184 mm,两者均在飞片速度v=113.07 m/s的冲击下仿真,得到靶板背对冲击部位的中心点位移如表5所示,金字塔夹芯板的变形仅为实心板的60.1%,以上结果足以证明金字塔芯层具有良好的抗冲击性能。

表5 金字塔夹芯板与实心板变形结果

3 不同参数金字塔夹芯板仿真

利用实验与仿真得到不同厚度飞片在不同速度下冲击不同参数芯层时后面板中心点的变形情况,如表6所示,从中可以发现仿真结果均与实验吻合较好,表明仿真模型在不同工况下也具有较高的准确性。

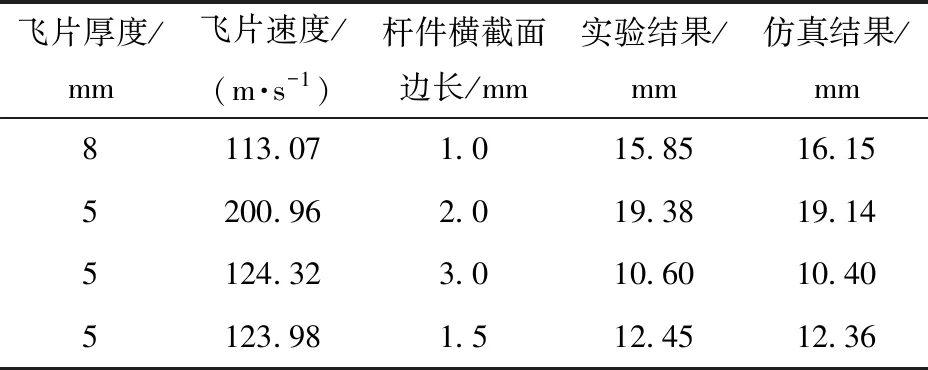
表6 不同工况后面板变形实验与仿真结果

在对不同结构参数进行实验的过程中发现,不同参数对金字塔夹芯板抗冲击性能影响较大,其芯层失效模式也不相同,如图14所示为芯层杆件截面边长为2 mm、厚度15 mm(后简称芯层B)的夹芯板受到5 mm厚飞片以200.96 m/s撞击时的变形情况,可以发现,芯层杆件并未发生如芯层A的实验中那样压溃屈曲,由于芯层B杆件更粗,其受冲击后发生屈曲的临界应力更大,在实验所示的冲击下,其主要发生的是如图14中右上角芯层侧视图所示的整体弯曲变形,同时由于冲量较大,前面板与芯层连接处出现了明显的破口。

图14 夹芯板B变形情况(左为芯层,右为芯层及前面板)

为研究不同结构参数以及冲击载荷对金字塔夹芯板抗冲击性能及破坏模式的影响,在验证仿真模型有效性的基础上,利用有限元仿真方式,对面板厚度、芯层杆件、冲击载荷大小等参数进行仿真研究。

3.1 前后面板厚度的影响

为探究前后面板厚度对金字塔夹芯板抗冲击性能的影响,在保证金字塔芯层结构参数以及总质量不变的情况下,改变前后面板厚度,得到的变形情况如表7所示,仿真中飞片厚度8 mm,速度113.07 m/s,金字塔芯层为芯层A。从表7中可以看出,较薄的前面板可以充分发挥芯层的吸能效果,有效降低后面板中心点变形,当前面板厚度大于后面板时,前面板越厚,芯层塑性吸能越小,同时后面板中心点变形越大。以上结论表明,在水下爆炸冲击载荷下,当夹芯板面板质量一定时,可以通过改变前后面板的厚度来改变夹芯板的抗冲击性能,前后面板厚度相同或前面板厚度小于后面板厚度的夹芯板,其抗冲击性能要明显优于前面板厚度大于后面板厚度的夹芯板,因此在设计夹芯板时,可以考虑将更多的质量分布在后面板上。

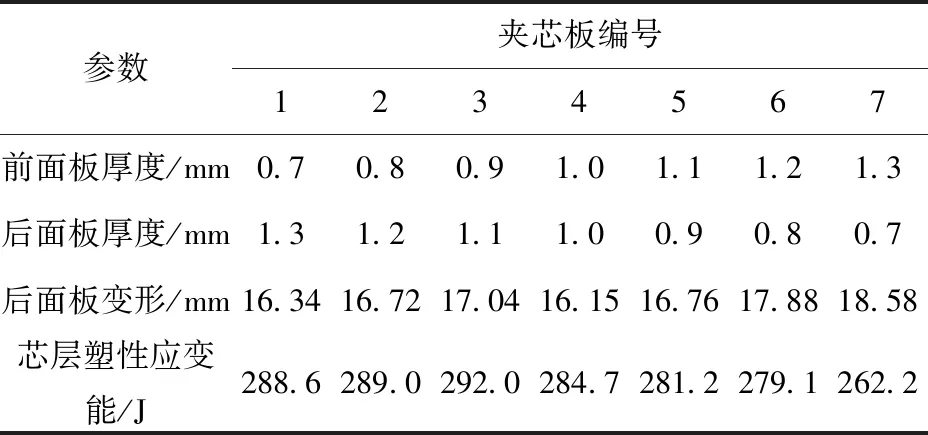
表7 不同厚度面板夹芯板变形情况

上述仿真在保证夹芯板面密度不变的前提下进行。Xue等[1]给出了评估靶板受到的无量纲化冲量:

(8)

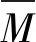
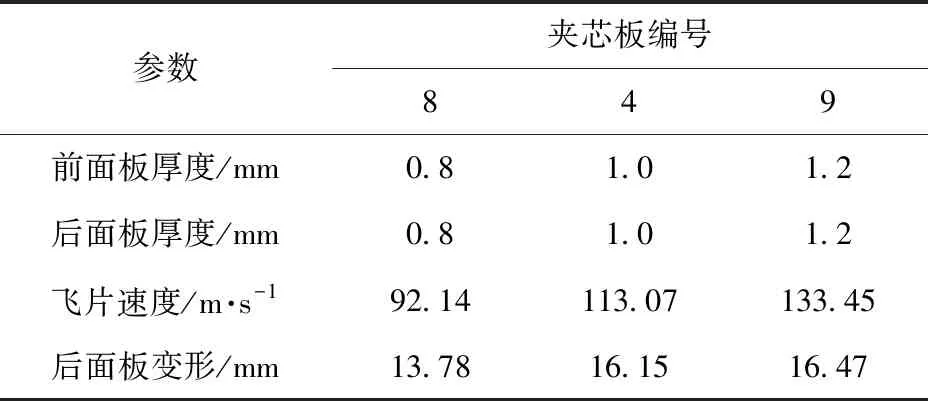
表8 相同无量纲冲量下夹芯板变形情况

3.2 芯层杆件粗细对抗冲击性能的影响

由图13可以发现,在芯层杆件的横截面边长不同的情况下,在受到相同的冲击时,金字塔夹芯板的变形模式以及破坏模式会有所改变,利用仿真对芯层B的金字夹芯板进行仿真,仿真中飞片速度为 113.07 m/s,将其结果与芯层A的结果进行对比,其前、后面板变形,芯层压缩量以及塑性应变能如表9所示。

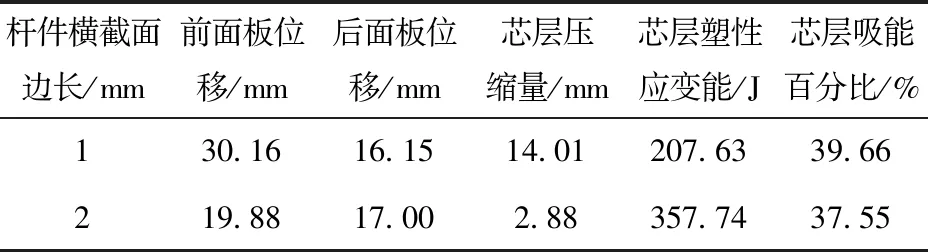
表9 不同芯层在相同载荷下的仿真结果

由表9可以看出,不同尺寸杆件对于金字塔夹芯板的变形和芯层吸能都有较大影响,芯层B相较于芯层A,其表现出更强的刚性。从芯层压缩量上看,在受到冲击时,芯层B更难被压缩,导致芯层与面板整体弯曲,胞元和胞元之间发生偏转,面板除中心点变形较大外,受载区域整体变形更大,即变形曲率半径更大。从吸能角度上看,芯层B塑性应变能比芯层A的更大,但芯层吸能百分比较小,其原因是在受到水下爆炸冲击载荷时,由于流-固耦合的影响,刚性较大的夹芯板,其受到的冲量也更大,芯层B的夹芯板整体吸收的能量也更多。

对芯层B的夹芯板施加更大速度的冲击,以保证其无量纲冲量与芯层A的夹芯板相同,得到的结果如表10所示,可以发现在此无量纲冲量下,芯层A的夹芯板相较于芯层B的夹芯板,有更好的抗冲击性能。

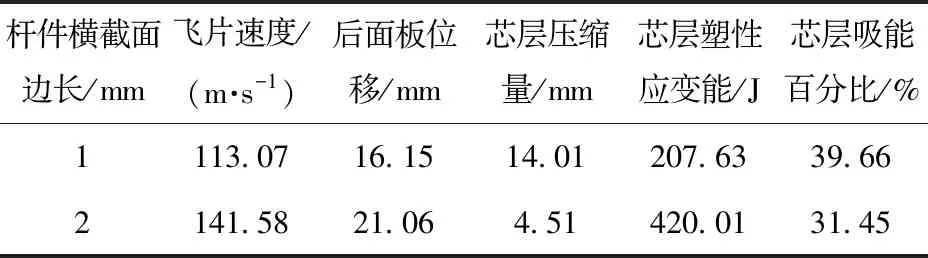
表10 不同芯层在相同无量纲冲量下的结果

3.3 冲击载荷对芯层变形的影响

考虑到实际情况中无法预测夹芯板受到的冲击大小,需要对夹芯板在不同冲击下的响应特点进行研究,利用仿真对芯层A和芯层B在受到不同速度的飞片冲击下的变形吸能进行研究。

不同冲击速度下两种夹芯板的后面板中心点变形如图15所示,从中可以发现两种芯层的后面板变形与飞片速度呈线性关系,对其进行线性拟合后发现两种芯层的拟合曲线几乎重叠。以上结果说明这两种芯层杆件粗细对于后面板变形几乎无影响,只影响其芯层的变形吸能模式。

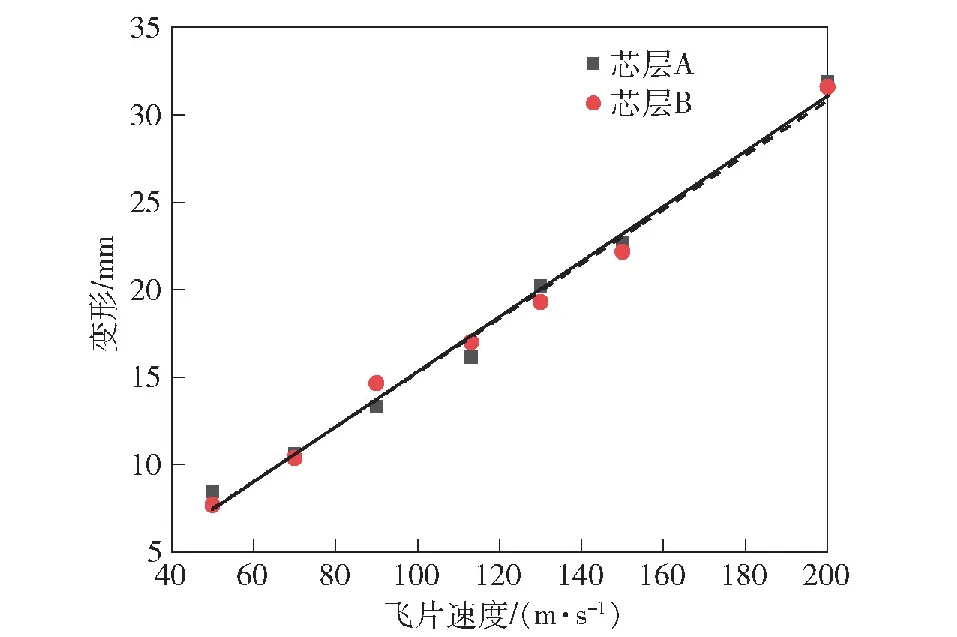
图15 不同飞片速度下夹芯板A后面板变形

不同冲击速度下芯层A夹芯板的各部分塑性吸能比例如图16所示。由图16可见:随着飞片速度的增加,芯层的吸能比例减小,后面板吸能比例明显增大,其原因为芯层逐渐被压实,将更多的冲量传递至后面板,导致后面板的变形增大;芯层B的塑性应变吸能结果与芯层A类似,芯层吸能比例也随着飞片速度增加而下降。

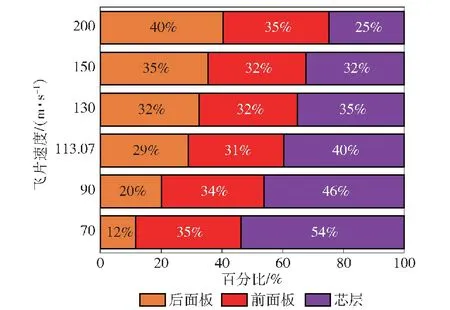
图16 不同飞片速度下芯层塑性变形能占比

3.4 金字塔夹芯板的多目标优化设计

基于上述研究,发现金字塔芯层的参数对其抗冲击性能影响较大,为提升其抗冲击性能,需寻找最优参数。在设计过程中,要同时考虑夹芯板的抗冲击性能以及夹芯板厚度及质量要求,就要对金字塔夹芯板进行多目标优化,以满足不同的工程需求。

对于金字塔夹芯板的优化,其优化问题可定义为

(9)

式中:u为夹芯板后面板中心点变形;m为夹芯板总质量;b为芯层杆件横截面边长;d为前后面板厚度;h为芯层厚度。决策变量的范围选取依据了实验及大量仿真结果。

为求得后面板中心点变形u与b、d、h参数的关系,就需构建代理模型,又称响应面模型。构建代理模型需要基于一定数量已知参数下的目标函数结果,因此需要进行大量的仿真,仿真将花费大量的计算资源并且耗费很长的时间。为减少仿真数量,本文采用拉丁超立方(LHS)方法对参数进行采样,让样本点分布更加合理。抽样总数为60组,其在空间中的分布如图17所示,从中可见样本点均匀地分布在整个空间内。

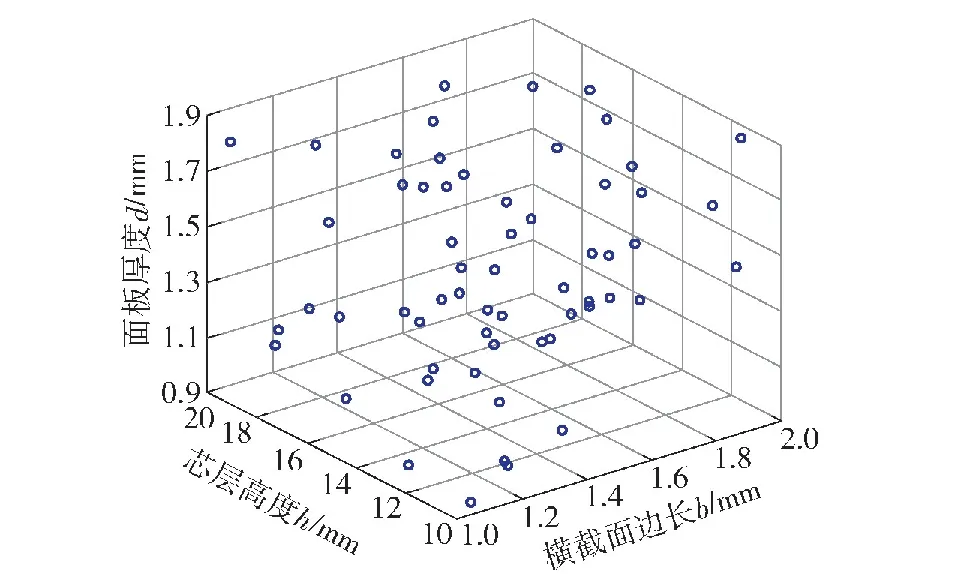
图17 LHS抽样结果

对抽样获得的不同参数的金字塔夹芯板进行仿真,仿真工况为:飞片厚度8 mm,飞片速度150 m/s,提取的后面板中心点变形如表11所示。

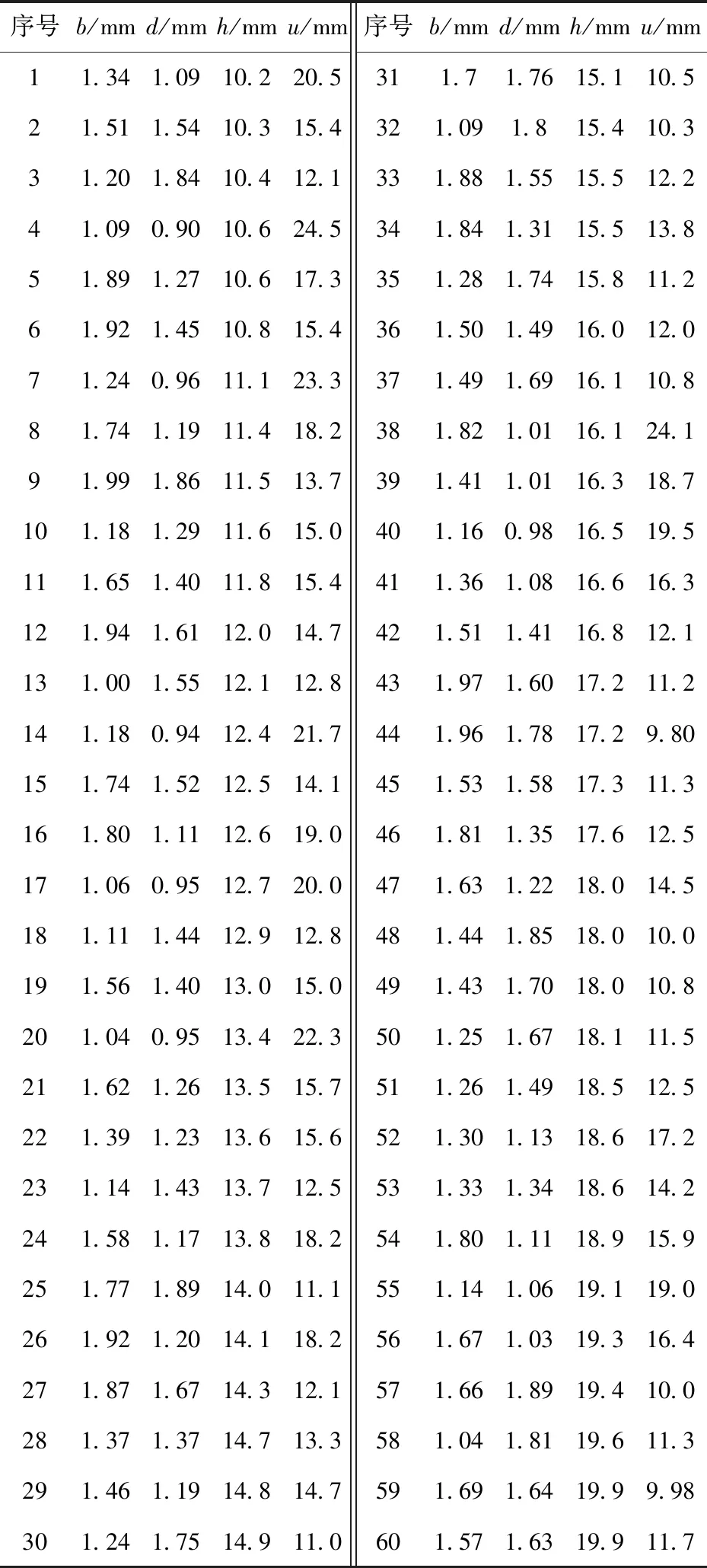
表11 LHS抽样点及对应变形结果

基于上述仿真结果,利用RBF神经网络建立代理模型,并对代理模型进行验证,利用确定系数R2、均方误差MSE和平均相对误差Reavg对代理模型进行检验,其表达式分别为

(10)

(11)

(12)

式中:n为样本量;yi为由仿真得到的结果;i为代理模型的预测结果;为仿真结果的平均值。构建的代理模型的确定系数R2=0.977 7,均方误差MSE=0.530 9,平均相对误差Reavg=3.37%,均在可接受范围。以上结果表明,利用RBF神经网络构建的代理模型拟合程度较高。

利用NSGA-Ⅱ方法对夹芯板质量和后面板中心点位移两个参数进行多目标优化,每一代种群数量200,变异概率0.05,经过500代之后,得到的Pareto前沿如图18所示,构建代理模型的60组数据也在图18中一并绘制。

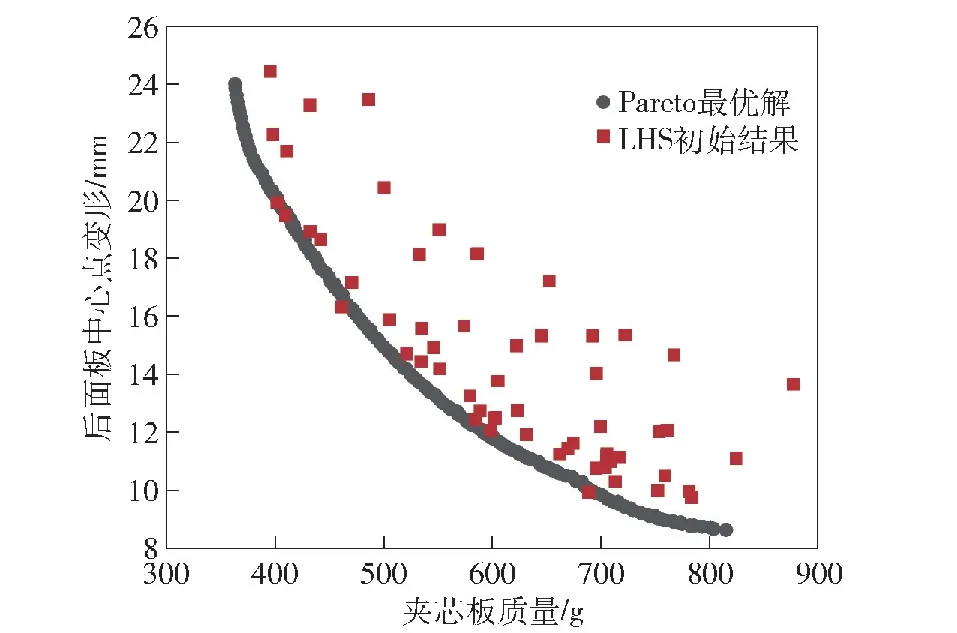
图18 Pareto最优解

由图18可以看出,得到的Pareto最优解集构成的Pareto前沿都在LHS抽样数据的左下方,Pareto最优解可以支配大部分初始数据,表明利用NSGA-Ⅱ算法得到的金字塔夹芯板优化问题的最优解具有可靠性。

为进一步检验代理模型和优化结果的可靠性,提取Pareto解集上的5个最优解进行后面板中心点变形的仿真验证,选点依据为:选择构建代理模型时最容易产生误差的点,即边界点,以及优化结果中拥挤度为无穷大的点,即Pareto前沿上两端的点,再随机从Pareto前沿中部选取3个点,得到的后面板变形结果如表12所示。

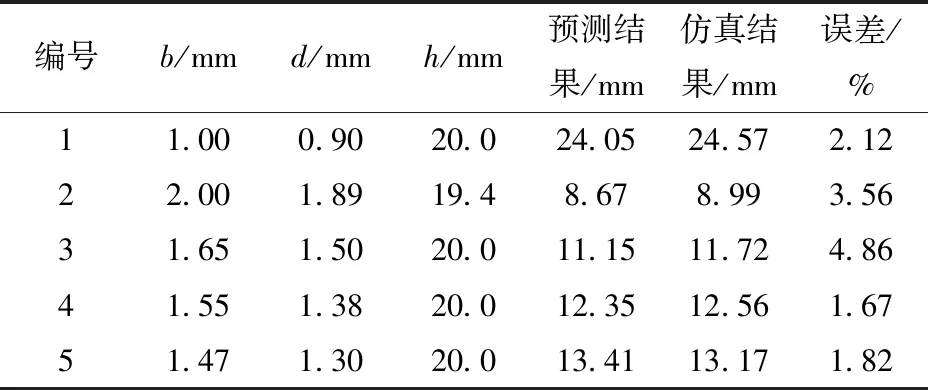
表12 部分最优解预测值与仿真值对比

表12中的结果表明,得到的最优解的预测值与仿真值误差均小于5%,进一步证明了本文构建的代理模型具有较高的准确性,保证了最优解的结果具有可靠性。利用此多目标优化方法对金字塔夹芯板进行参数选取,其结果对金字塔芯层参数的选取具有指导意义。

4 结论

本文利用等效水下爆炸冲击加载实验装置对金字塔点阵夹芯板进行实验,并利用仿真对不同参数夹芯板的抗冲击性能和破坏模式进行了分析。得到主要结论如下:

1)建立的仿真模型计算结果与实验结果误差较小,证明了其有效性;对于金字塔夹芯板,其受到水下爆炸冲击后,动态响应分为三个阶段:整体变形同时变形向中心发展、芯层压缩、整体变形。

2)对于夹芯板A,其单位质量的芯层吸能是单位质量面板吸能的6.86倍以上,与相同质量的实心板相比,其变形为实心板变形的60.1%,证明金字塔芯层具有良好的抗冲击和吸能能力。对于同一芯层,相同无量纲冲量下,芯层质量占夹芯板质量越高,夹芯板抗冲击性能越好,面板总厚度一定时,拥有较厚后面板的夹芯板抗冲击性能更优。

3)不同参数的金字塔夹芯板变形吸能模式不同,芯层A主要为结构杆件的屈曲和整体的压溃,芯层B为芯层整体的弯曲变形,其屈曲并不明显。芯层A与芯层B在相同冲击下夹芯板中心点变形几乎相同,芯层A密度小于芯层B,因此考虑夹芯板质量的前提下,芯层A的抗冲击性能要优于芯层B。

4)夹芯板中心变形与飞片冲击速度呈线性关系,随着冲击速度的增加,芯层的吸能占比下降,后面板吸能占比上升。

5)基于NSGA-Ⅱ方法对金字塔夹芯板质量和变形进行优化设计,优化结果具有可靠性,该方法对金字塔夹芯板的设计有指导作用。