木质复合门结构优化仿真分析研究

乔雅煊 李贤军 吕建雄 王海东 郝晓峰*

（1.中南林业科技大学材料科学与工程学院，湖南 长沙 410004；2.索菲亚家居股份有限公司，广东 广州 510000）

我国木质门产业已进入快速发展期，2021 年全国木门行业总产值达到1 603 亿元，同比增长2.1%[1]。木质门包括实木门、实木复合门和木质复合门3 大类，其中木质复合门是目前市场上所占份额最大的木门种类。这类木门以人造板为原材料，材料来源广、理化性能优良、成本较低，具有隔音、隔热、强度高等特点，因此被广泛用于商业和民用家居领域[2]。

木质复合门由门扇和门框组成，门扇结构主要由骨架、填充料、表板三层结构复合而成。其中，门扇骨架材料常使用单板层积材（LVL），表板为中密度纤维板（MDF），填充料为空心刨花板或蜂窝纸。这些木质材料会从使用环境中吸收或解吸水分而发生干缩湿胀，进而使木质复合门产生变形[3-4]。干缩湿胀是木质材料固有属性，通常可用干缩湿膨胀系数对其定量表征[5-7]。在使用过程中，由于组成木质复合门三层复合结构的木质材料干缩湿膨胀系数不同，因此导致木质复合门门扇翘曲、开裂或局部变形等问题。其中，门扇中的边梃、中档处常发生弯曲或反翘，致使门扇立面不在同一平面内，造成门扇开关不灵活[8-11]。选择合适的结构并对生产工艺流程进行控制，可最大程度消除因木质材料自身属性和外在环境带来的影响[12-14]。有研究表明，通过在边梃上开设应力释放槽、增加中横框数量和改善门扇饰面材料等方法优化门扇结构，可以减小门扇变形[15-17]。也有研究通过对门扇骨架结构进行优化以提升稳定性。李萍[18]提出使用交错复合实木板压制而成的家具面板，在保证产品外观属性的前提下，使其稳定性显著提升。王世松[19]设计一种抗变形门扇骨架，左右对称两个门挺分别与上下对称的两个门帽相互榫卯连接成型，并在门骨架内侧的四个顶角处均设有加强块，加强了门扇的防变形能力。卢达权[20]采取在门板凹槽内固定不易变形的金属型材，保证了门板不会在潮湿环境下拱起变形。此外，调整门铰链数量和安装位置也能提高门扇的尺寸稳定性[21-22]。

以上方法在一定程度上解决了木质复合门变形问题，为了精准量化分析门框架、填充料及表面板对木质复合门变形的影响规律，本研究基于有限元模型，在湿度变化条件下，定量表征木质复合门门扇框架不同组坯方案的吸湿变形情况，优化影响门扇变形的设计变量，以获得最佳的木质复合门组坯结构。

1 材料与方法

1.1 试验材料

试验用材：门扇骨架材料为单板层积材（LVL），门扇表板材料为中密度纤维板（MDF），取自索菲亚华鹤门业有限公司。LVL厚度分别为25 mm和40 mm；MDF厚度分别为5.7 mm和22 mm。

1.2 试验设备

电子天平，TE214S /210 g(0.1 mg)，梅特勒托利多上海有限公司；电热鼓风干燥箱，101-3AB，天津市泰斯特仪器有限公司；电子数显游标卡尺，MNT-150T，桂林广陆数字测控有限公司。

1.3 湿膨胀系数测定

不同原材料供应商检测3个批次，在同一批次同一板材9个区域内各采样30个，厚度为板材厚度，每种规格15个样品。按照GB/T 1927.8—2021《无疵小试样木材物理力学性质试验方法 第8部分：湿胀性测定》规定测定木材湿膨胀系数，木材含水率按照GB/T 17657—2013《人造板及饰面人造板理化性能试验方法》进行测定。

1.4 有限元模型建立

1.4.1 湿应力基本方程

在吸湿情况下，弹性体的应变分量由以下两部分叠加而成：

1）自由膨胀引起的应变分量，该分量服从湿膨胀规律：

2）在湿膨胀时因弹性体内各部分之间相互约束引起的应变分量，这些应变分量和湿应力之间服从Hooke定律。因此，吸湿情况下的物理方程为：

式中：εx，εy，εz分别为x，y，z方向上的线应变，Pa；σx，σy，σz分别为x，y，z方向上的正应力，Pa；E为材料弹性模量，Pa；μ为泊松比；γxy，γxz，γyz为xy，xz，yz方向上的剪切应变，Pa；τxy，τxz，τyz为xy，xz，yz方向上的剪应力，Pa；β为湿膨胀系数；C为湿度，ΔC为湿度变化量，%RH。

为获得在试验湿度变化过程中不便直接测量的门扇框架结构变形情况，现使用有限元分析软件ABAQUS进行分析。上述方程结果与热应力场中的数学模型基本相同，因此湿应力有限元分析可借鉴热应力场模型[23]。

1.4.2 材料属性设定

为保证模型模拟木材的各向异性，需要9 个弹性常数，即径向、弦向、轴向三个方向上的弹性模量、泊松比和剪切弹性模量。模型材料的弹性常数如表1 所示。本研究中木质门门扇结构整体几何模型的尺寸为2 000 mm× 850 mm。

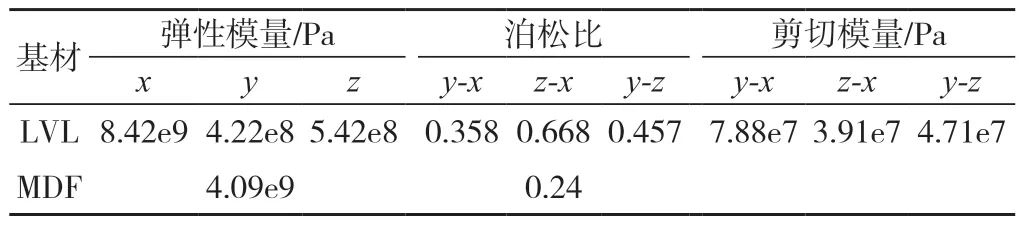
表1 基材的弹性常数Tab.1 Elastic constants of basic materials

1.4.3 初始条件和边界条件

门扇结构在开始吸湿变形时含水率为10%。吸湿分析时，对门扇结构施加相对湿度载荷17%，在门扇结构边界施加约束，进行铰链固定。

本研究根据现有门扇结构，拟定7 种组坯方案，如图1 所示。对7 种方案进行模拟分析，选取最优方案后，以表板厚度、骨架厚度和单边宽度为设计变量，对方案进行尺寸优化。

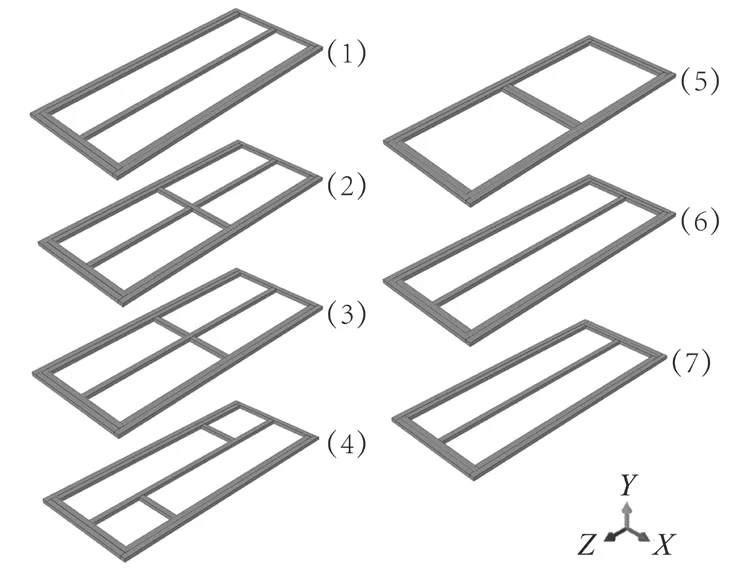
图1 7 种框架结构方案Fig.1 Seven frame structures

2 结果与分析

2.1 湿膨胀系数分析

2.1.1 MDF湿膨胀系数分析

由图2 可知，不同厚度MDF 3 个方向（长度、宽度及厚度）的湿膨胀系数存在显著性差异，其中5.7 mm MDF厚度方向平均湿膨胀系数分别为长度和宽度方向的26.0 倍和19.5 倍，中心处厚度湿膨胀系数较边缘处低。这可能是MDF热压过程中边部密度略低于心部，边缘孔隙略大，其吸湿位点更多所致。22 mm MDF厚度方向平均湿膨胀系数是长度和宽度方向的23.7倍和24.5 倍。22 mm MDF厚度方向平均湿膨胀系数是5.7 mm MDF的1.1 倍，厚度越大湿膨胀系数越大，其原因可能是由于MDF的尺寸稳定性随密度增加而下降，密度越大，由内应力释放产生的回弹力越大，而这种回弹力为不可逆[26-27]。

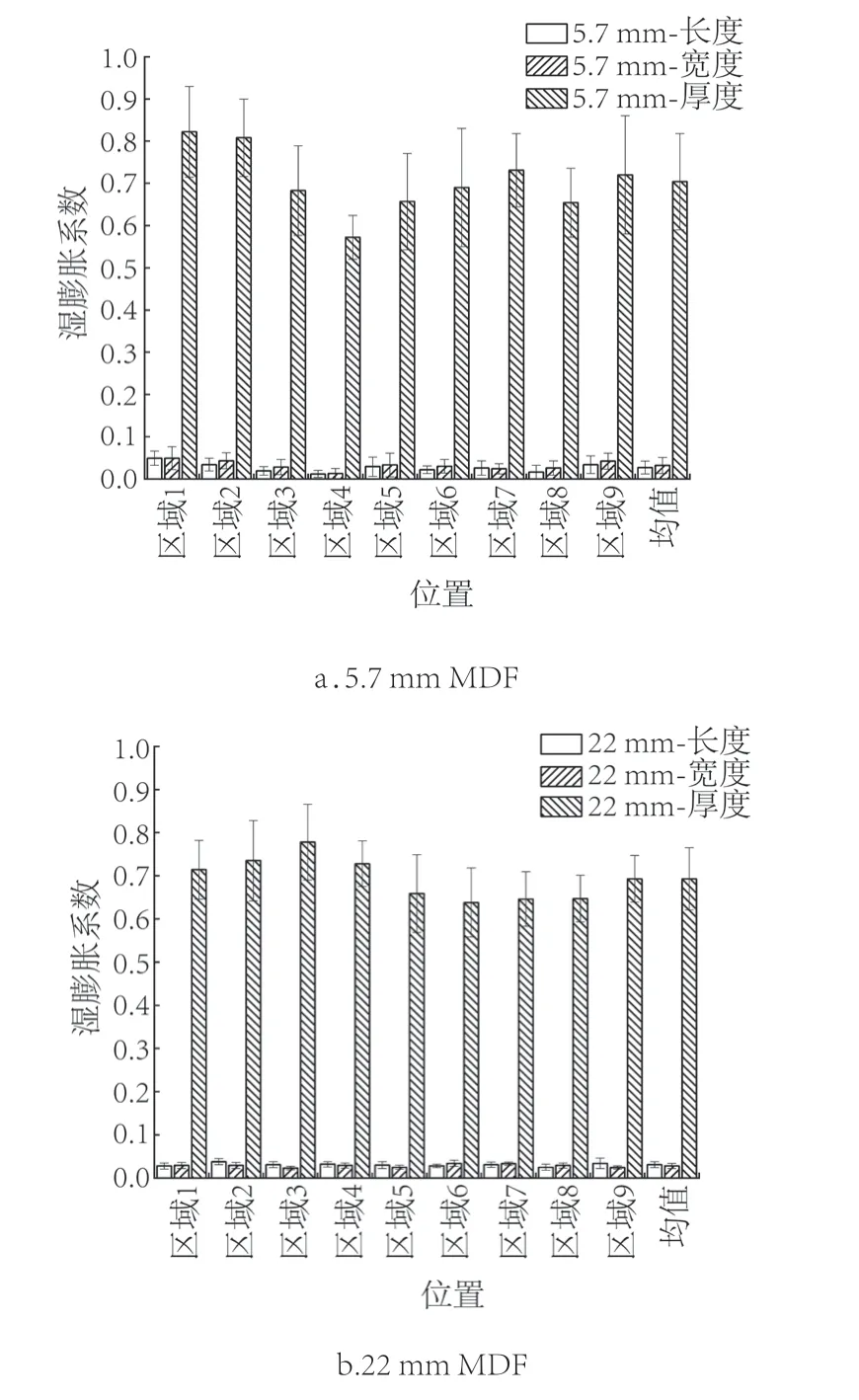
图2 不同厚度MDF的湿膨胀系数Fig.2 Hygroscopic expansion coefficient of MDF with different thickness

2.1.2 LVL湿膨胀系数

由图3 可知，厚度为25、40 mm的 LVL顺纹、横纹及厚度方向的湿膨胀系数差异性均不显著（P=0.59，P=0.39，P=0.36），说明两者间同方向的湿膨胀系数差别不大。但同一厚度LVL横纹与厚度方向差异性较大（P=0.000 04，P=0.000 3），其中25 mm LVL横纹方向平均湿膨胀系数比厚度方向高35.6%，40 mm横纹方向平均湿膨胀系数比厚度方向高24.4%。顺纹方向湿膨胀系数最小，这主要是因为LVL顺纹为木材纵向，木材纵向湿胀系数较小；而LVL厚度与横纹方向自由湿胀差异较大，这主要是因为横纹为木材弦向，厚度方向为木材径向，木材径向湿胀系数较弦向小所致[28-35]。

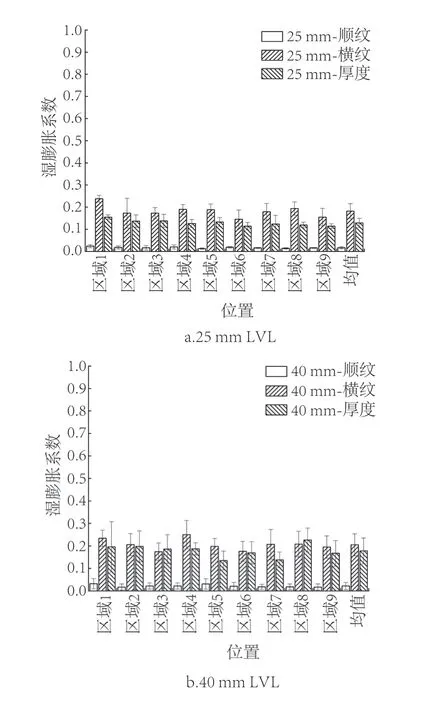
图3 不同厚度LVL的湿膨胀系数Fig.3 Hygroscopic expansion coefficient of LVL with different thickness

由上述分析可知，MDF厚度方向湿膨胀系数远远大于其长度和宽度方向，且厚度越大湿膨胀系数越大。不同厚度LVL湿膨胀系数差别不大，但同一厚度LVL顺纹、横纹与厚度方向差异性较大。数据对比表明，MDF厚度方向湿膨胀系数最大，LVL顺纹方向湿膨胀系数最小。

本研究选用LVL作为框架材料，MDF为表板材料。根据湿膨胀系数分析，LVL单元条的组坯方向如图4所示。

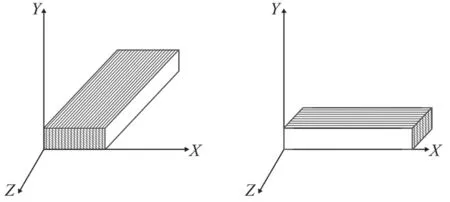
图4 单元条组坯方向Fig.4 The orientation of the unit

2.2 木质复合门结构优化分析

2.2.1 框架结构对门扇变形的影响

运用ABAQUS对7种框架组坯结构进行变形模拟。根据工厂门扇现有尺寸，框架厚度固定为28 mm，单元条宽度固定为40 mm，门扇含水率模拟由10%升至17%。

如图5所示，7种组坯结构综合变形量（U）的变形范围为2.732～3.201 mm，宽度方向变形量（U1）变形范围为2.718～3.201 mm，厚度方向变形量（U2）变形范围为0.241～0.248 mm，长度方向变形量（U3）变形范围为1.927～2.383 mm。

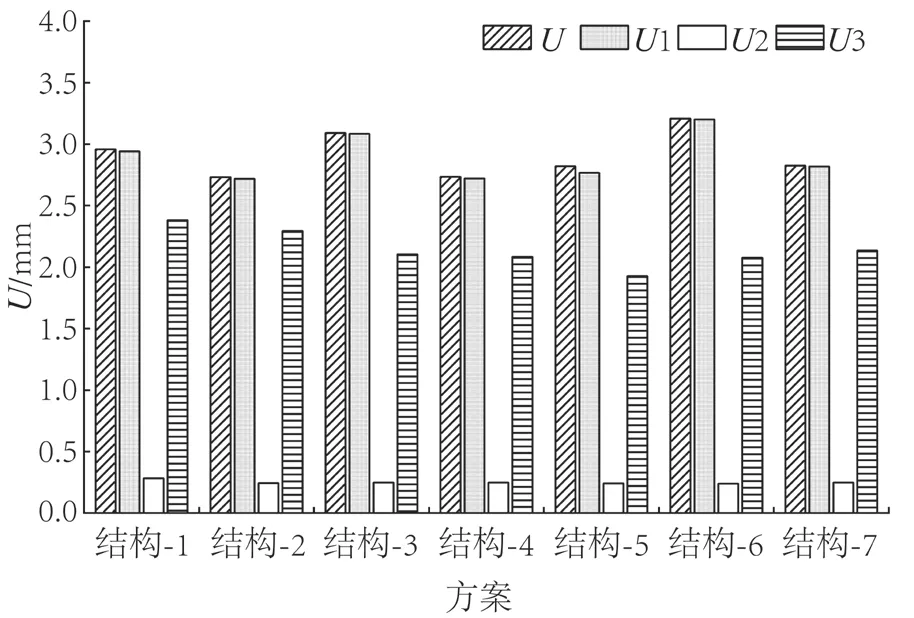
图5 7 种框架结构变形量Fig.5 Deformation of seven frame structures

以门扇框架结构-1为基础，分别分析其余6种方案。结构-2在结构-1的基础上增加了中横梃，结构-1的U为2.957 mm，结构-2的U为2.732 mm，变形量相比结构-1减小了7.6%。根据图6的7种方案变形云图可知，结构-2右边梃受中梃限制，中间部位变形明显减小，造成这种现象的原因是中梃长度方向为LVL纵向，变形较小，其限制了右边梃宽度方向变形。结构-2与结构-3框架组坯方式大致相同，区别在于结构-2采用完整中横梃和2个分开的中竖梃形式，结构-3采用完整中竖梃和2个分开的中横梃形式。结构-2的U1为2.718 mm，结构-3的U1为3.084 mm，比结构-2高出13.5%，可以看出带有完整中横梃的组坯结构能更好地抑制门扇宽度方向的变形。

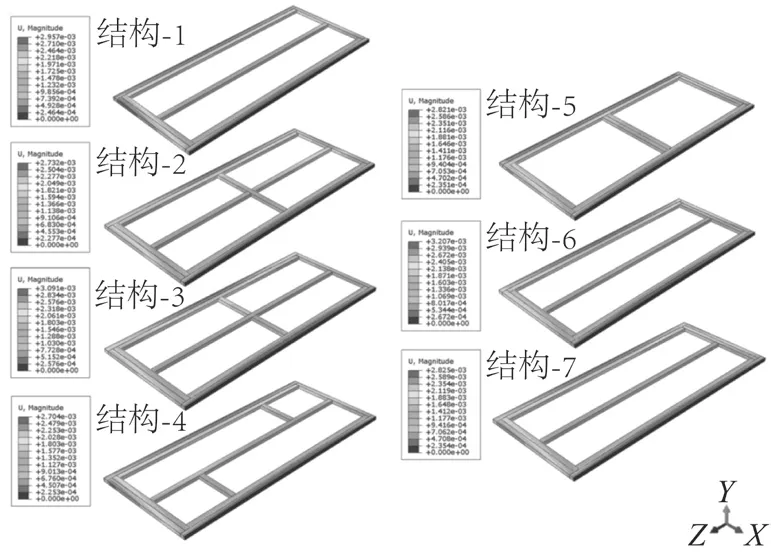
图6 7 种框架结构变形云图Fig.6 Deformation cloud diagram of seven frame structure

结构-3和结构-4与结构-1相比，增加了2个中横梃，并且分布于中竖梃两侧，结构-3的U为3.091 mm，变形量相比结构-1增加了4.5%，其原因是中竖梃的横向变形较大，增加的左右对称中横梃无法起到制约效果。结构-4与结构-3的不同之处是将分开的2个中横梃错开组坯，结构-4的U为2.734 mm，相比结构-1变形量减小了7.5%，可能是错开的组坯形式将变形分散，使得这种结构可有效抑制变形。

结构-5与结构-1相比，去掉了中竖梃，采用中横梃形式，U下降了6.4%，变形减小的原因与结构-2相同。

结构-6与结构-7框架组坯方式大致相同，区别在于结构-6的左右边梃与上下边梃为交叉组合形式（如图7c），结构-7为边梃包上下边梃组合形式（图7b）。与结构-1相比，结构-6变形量增加了8.4%，而结构-7下降了4.4%。根据模拟结果可知，结构-6的U1为3.201 mm，U3为2.076 mm，结构-7的U1为2.819 mm，比结构-6降低11.93%，U3为2.111 mm，比结构-6增加1.98%。整体来看，边梃包上下边梃组合形式优于左右边梃与上下边梃交叉组合形式，其原因是边梃包上下边梃连接处接触面较大，更能起到牵制作用。

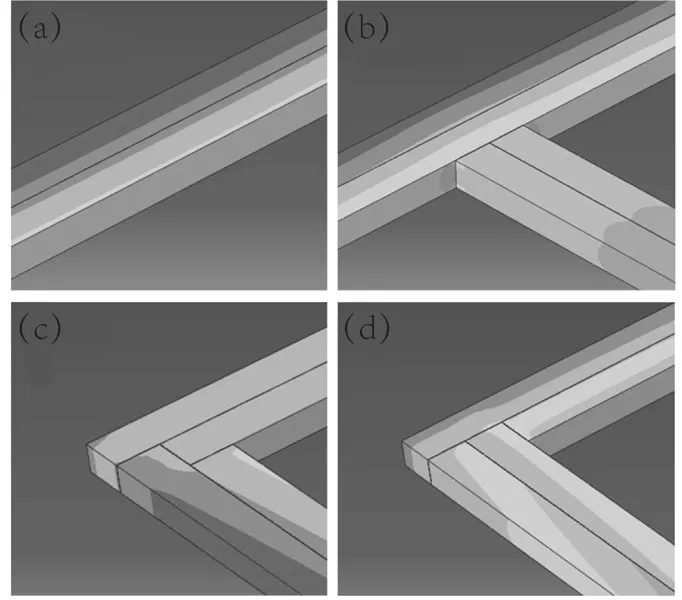
图7 不同连接方式Fig.7 Different connection modes

综合7种结构方案可知，门扇的变形主要取决于连接方式和组坯方式。结构1～5门变形主要发生在未固定边梃中部及上下边梃交汇角隅处，结构6～7门变形主要集中在未固定边梃的中间位置，结构-2的变形最小，结构-6的变形最大。根据图6和图7可以看出，中横梃可以抑制未固定侧边梃的变形，带有中横梃的组坯结构框架整体变形量会比不带中横梃的结构框架整体变形量小。

2.2.2 门扇框架与表板交互作用分析

根据2.1中对MDF 3个方向湿膨胀系数的分析，MDF厚度方向的湿膨胀系数远大于其长度和宽度方向湿膨胀系数。加入表板后，7种方案的U1和U3均变小，U2均增大，加入表板会加剧整体结构厚度方向的变形，但如图8所示，7种框架整体变形均减小，说明表板对框架结构的变形抑制效果显著。根据7种结构的变形云图（图9），带有中横梃的框架，如结构-2和结构-5可显著抑制未固定侧区域的变形，使U1减小；结构-7的变形量最小，且变形多集中在框架角隅处。

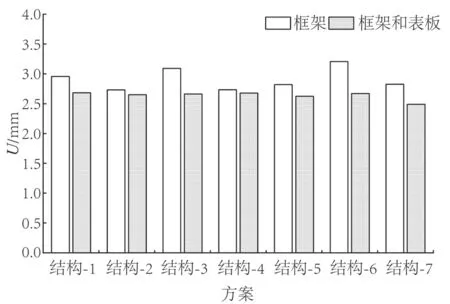
图8 7 种框架和表板结构变形量Fig.8 Deformation of seven frames and surface plates

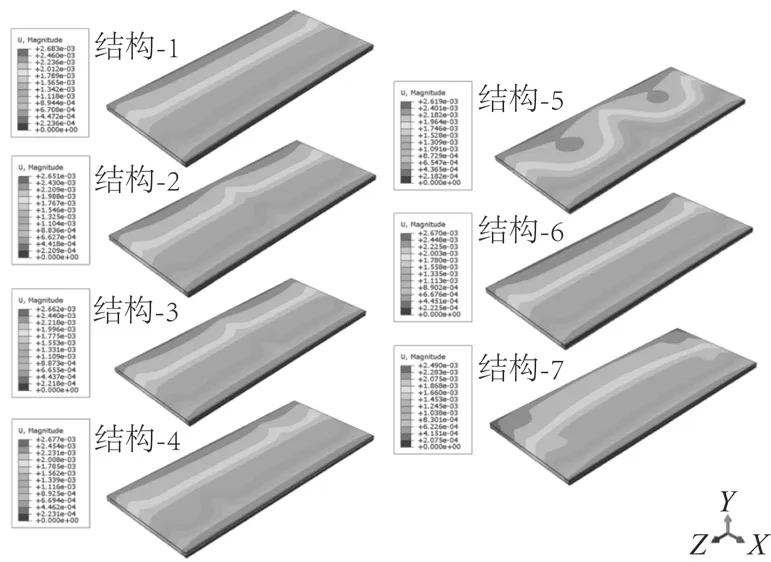
图9 7 种框架和表板结构变形云图Fig.9 Deformation cloud diagram of seven frames and surface plates

表板对框架变形量大的结构抑制变形的效果更显著，如结构-3与结构-6在加入表板组坯后，变形量分别下降了13.90%和16.7%，但是其最终的整体变形量仍不是最小。结构-5与结构-7相较于其他结构变形量较小。

2.2.3 门扇框架优化结果

根据以上分析，对7种方案进行结构优化，采用边梃包上下梃的组合形式，并加入中横梃，最终得到新的优化方案，如图10所示。优化结构的变形量相对于变形量较小的结构-5和结构-7，分别下降了7.6%和2.8%。

图10 优化方案Fig.10 Optimization scheme

2.3 门扇结构尺寸优化分析

选取最优方案后，以表板厚度、骨架厚度和边梃宽度为设计变量，对方案进行优化，如图11所示。

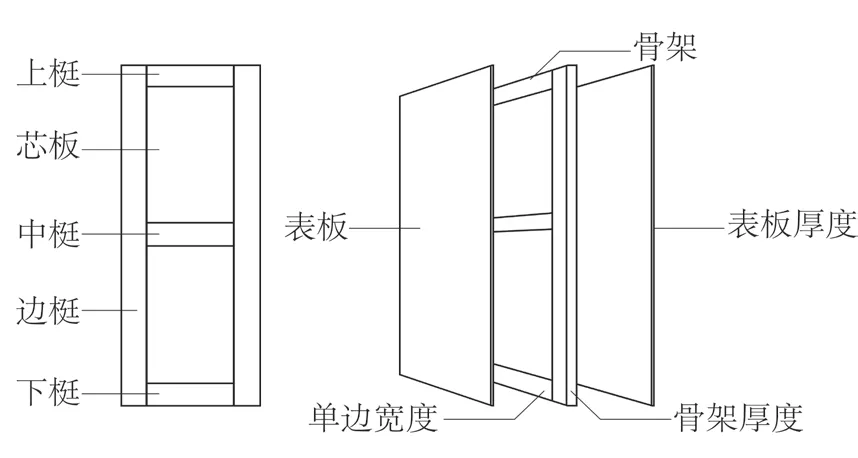
图11 木质复合门门扇结构Fig.11 Structure of wood-based composite door leaf

2.3.1 表板厚度对门扇整体变形的影响

根据工厂门扇现有标准尺寸，固定框架厚度，在一定范围内改变表板厚度，门扇含水率模拟从10%上升至17%。以优化方案为基础，选择宽度为25 mm和40 mm的单元条进行组坯，分别获得单边宽度为75 mm和80 mm 2种规格的门扇。

根据模拟结果，单边宽度75 mm的方案变形最大的区域仍为未固定侧边梃角隅处，上下边梃变形量其次，厚度方向变形量最小。如图12所示，随着表板厚度的不断增加，门扇框架的整体变形量呈现先减小后增大的趋势。当表板厚度为3 mm时，门扇框架的整体变形量最小，变形量为2.270 mm。相比于厚度为2 mm和6 mm，其变形量分别降低了1.73%和4.8%。门扇框架宽度方向的变形量（U1）随着表板厚度的增加，呈现出逐渐变小的趋势；门扇框架厚度方向的变形量（U2）和长度方向的变形量（U3）随着表板厚度的不断增加均呈现上升趋势。

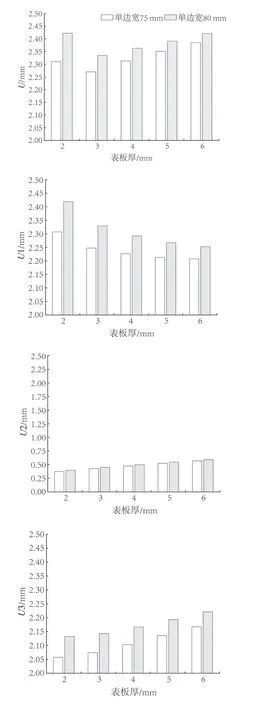
图12 不同厚度表板的门扇变形Fig.12 Deformation of the door leaf with different thickness of the panel

单边宽度80 mm的方案变形趋势与单边宽度75 mm的方案相同，即随着表板厚度的不断增加，门扇框架的整体变形量呈现先减小后增大的趋势。当表板厚度为3 mm时，门扇框架的整体变形量最小，变形量为2.335 mm，相比于单边宽度75 mm的方案，变形量增加了2.9%。

当表板过薄时，不能起到和框架相互抑制变形的作用，又因为MDF随着厚度的增加，厚度方向的湿膨胀系数会不断变大，因此表板厚度越厚，门扇变形量会越大。当表板厚度为3 mm时，门扇变形量最小。

2.3.2 框架厚度对门扇整体变形的影响

根据以上结果可知，当表板厚度为3 mm，门扇变形相对较小，因此将表板厚度固定为3 mm，在一定范围内改变框架厚度。

如图13所示，根据模拟结果可知，单边宽度75 mm的方案与单边宽度80 mm的方案均随着框架厚度不断增加，门扇综合变形呈现先减小后增加的趋势。这种变化趋势可能是因框架厚度过薄或过厚，影响其与表板的互相牵制。框架厚度过小不能抑制整体结构的变形，框架厚度过大则会加剧整体结构的变形。当框架厚度为28 mm时，综合变形最小，单边宽度75 mm的方案变形量为2.270 mm，单边宽度80 mm的方案变形量为2.336 mm，比前者增加了2.9%。

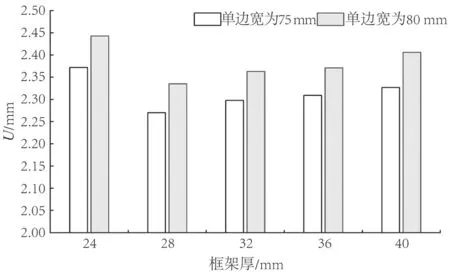
图13 不同厚度框架的门扇变形Fig.13 Deformation of the door leaf with different thickness of the frame

2.3.3 单边宽度对门扇整体变形的影响

从表板和框架的优化中可知，单边宽度75 mm方案的变形量皆小于单边宽度80 mm方案的变形量，因此用宽度为25 mm的LVL单元条组坯效果优于宽度为40 mm的单元条。这是因为框架材料25 mm LVL的厚度方向干缩系数比40 mm LVL的更小。现选择宽度为25 mm单元条进行组坯，分别获得单边宽度为50、75 mm和100 mm的3组方案。固定表板厚度为3 mm，框架厚度为28 mm，模拟结果如图14所示。

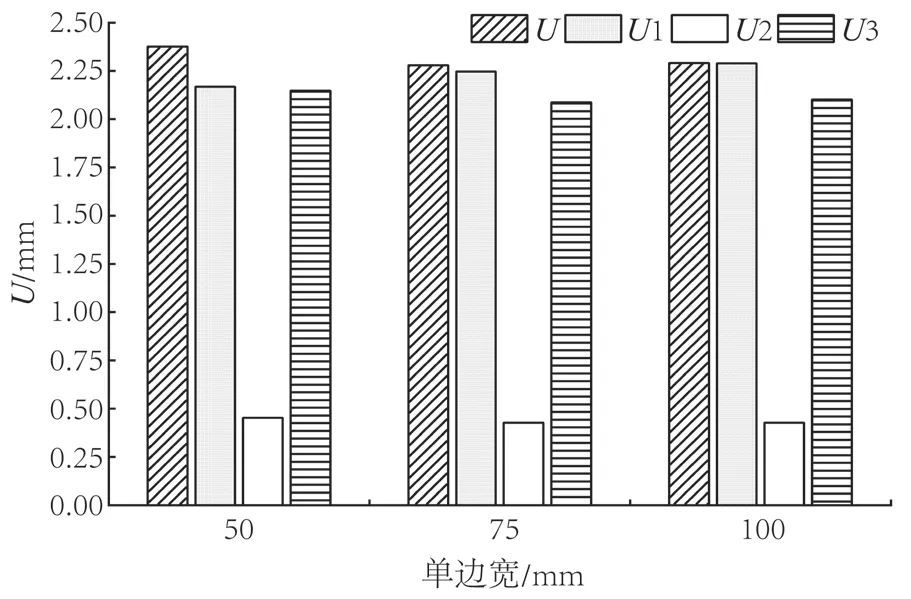
图14 不同单边宽度的门扇变形Fig.14 Deformation of the door leaf with different side width of the frame

随着单元条的增加，门扇综合变形量呈现先减小后增加的趋势，宽度方向变形量（U1）随着单元条的增加而减小；厚度方向变形量（U2）随着单元条的增加，变化不大；长度方向变形量（U3）随着单元条的增加，先减小后增加。

当单边宽度为75 mm时，门扇变形量最小，变形量为2.28 mm，相比单边宽度为50的方案，变形量减小了4.5%。

综上所述，表板和框架过薄不能抑制框架结构的变形，过厚则会加剧整体框架结构的变形。25 mm宽单元条组坯方案优于40 mm宽单元条组坯方案。最后获得的最佳组坯方案为：表板厚度为3 mm，框架厚度为28 mm，单边宽度为75 mm。

3 结论

本研究针对木质复合门门扇变形问题，通过分析木质复合门基材的湿膨胀系数，结合有限元数值模拟仿真，定量分析了在湿度变化的条件下木质复合门门扇的吸湿变形机制，对木质复合门组坯进行优化，获得理想的木质复合门门扇组坯方案。主要结论如下：

1）不同厚度MDF 3 个方向（长度、宽度及厚度）湿膨胀系数存在显著性差异，厚度方向湿膨胀系数远大于长宽方向的湿膨胀系数，厚度越大湿膨胀系数越大。厚度为25 mm与40 mm LVL同方向的湿膨胀系数差别不大，但同一厚度LVL顺纹与横纹和厚度方向差异性较大。

2）框架结构的变形主要集中在未固定侧边梃区域，添加中横梃可以有效抑制框架结构的变形。加入表板后，7 种结构的变形量均变小，表板和框架产生的交互效果明显，可以互相抑制变形。

3）随着表板厚度和框架厚度的不断增加，门扇框架的整体变形量呈现先减小后增大的趋势。25 mm宽单元条组坯方案的变形较小，因此该研究的最佳组坯方案为：表板厚度为3 mm，框架厚度为28 mm，单边宽度为75 mm。