竹帘竹胶合板弹性常数的动态测试与分析
兰昕苑 谷晓雨 陈清平 许 斌 杨小军 王 正*
(1.南京林业大学材料科学与工程学院,江苏 南京 210037;2.福建鑫恒达车厢底板有限公司,福建 三明 366035)
我国是全球竹子的主产国,拥有丰富的竹材资源。与木材不同,竹子很少直接作为建材等使用。多年来,学者们对不同结构竹复合材料的技术可行性开展了研究[1-5],其中包括重组竹、竹胶合板等。竹胶合板是以带沟槽的等厚竹片为构成单元,并经胶合压制得到的人造板材。该材料具有硬度高、抗折、抗压性能好等优点,用途广泛,可用于建筑、交通运输和家具等领域。随着我国经济水平的不断增长,人们的消费结构有所变化,对于家具行业、制造业等林业产业的需求量在不断增加[6],竹材作为一种绿色、可再生资源,凭借加工能耗少、环境污染小等独特的优点,使得其作为建材来代替部分木材有了更多的可能性,在“双碳”背景下,对于发展循环经济、改善生态环境等方面发挥了重要作用[7]。
弹性模量、剪切模量和泊松比是衡量竹胶合板力学性能的重要弹性常数。根据现行规范GB/T 13123—1991《竹编胶合板》[8]和LY/T 1575—2000《汽车车厢底板用竹材胶合板》[9]要求,一般采取静力学破坏试验测试竹胶合板的弹性常数和破坏机理分析[10-14]。
近年来,利用动态振动法测试木材及复合材料弹性常数的研究报道较多[15-18]。同时,许多研究使用概率方法来考察材料的力学性能[19-21]。王正等[22]采用悬臂板瞬态激励法,并通过改进应变片的贴法,实现了动态同步测试木材与MDF的弹性模量、剪切模量和泊松比。Giaccu等[23]基于悬臂板瞬态激励法,动态测试了3 层CLT的弹性模量和滚动剪切模量,并通过有限元分析,确定该方法体现了CLT的全局弹性特性。竹胶合板行业虽然采用静态法测试其弹性常数,但静态法会对材料造成破坏,并且其操作繁琐,依赖高成本的设备和高技术人员。因此,引入快速、简便、准确、可靠的动态振动法测试竹胶合板弹性常数尤为重要。
鉴于此,本文采用动态法测试竹帘竹胶合板的弹性模量,剪切模量和泊松比,探究其材性属性,并对竹胶合板的质量进行分析,以期将其运用于生产检测环节,进而提升产品的质量。
1 竹帘竹胶合板弹性模量,剪切模量和泊松比的动态测试
1.1 试验材料
竹帘竹胶合板1块,尺寸为2 440 mm(l)×2 440 mm(b)×12 mm(h),福建鑫恒达车厢底板有限公司。该板的中心层厚度为2.5 mm,其余层厚度为1.8 mm,两侧用薄木装饰,其热压后压缩率为15%,竹胶合板成品厚度为12 mm(±0.5 mm)。竹胶合板的花纹面为P面,木纹面为N面,进行上P下N,上N下P两组测试,如图1所示。

图1 竹胶合板P面和N面定义Fig.1 Definition of P-side and N-side of bamboo plywood
如图2 所示,以长度方向平行于中心层竹片排列的竹胶合板试件定义为纵向(x向),垂直于其排列的为横向(y向)试件的具体参数见表1。
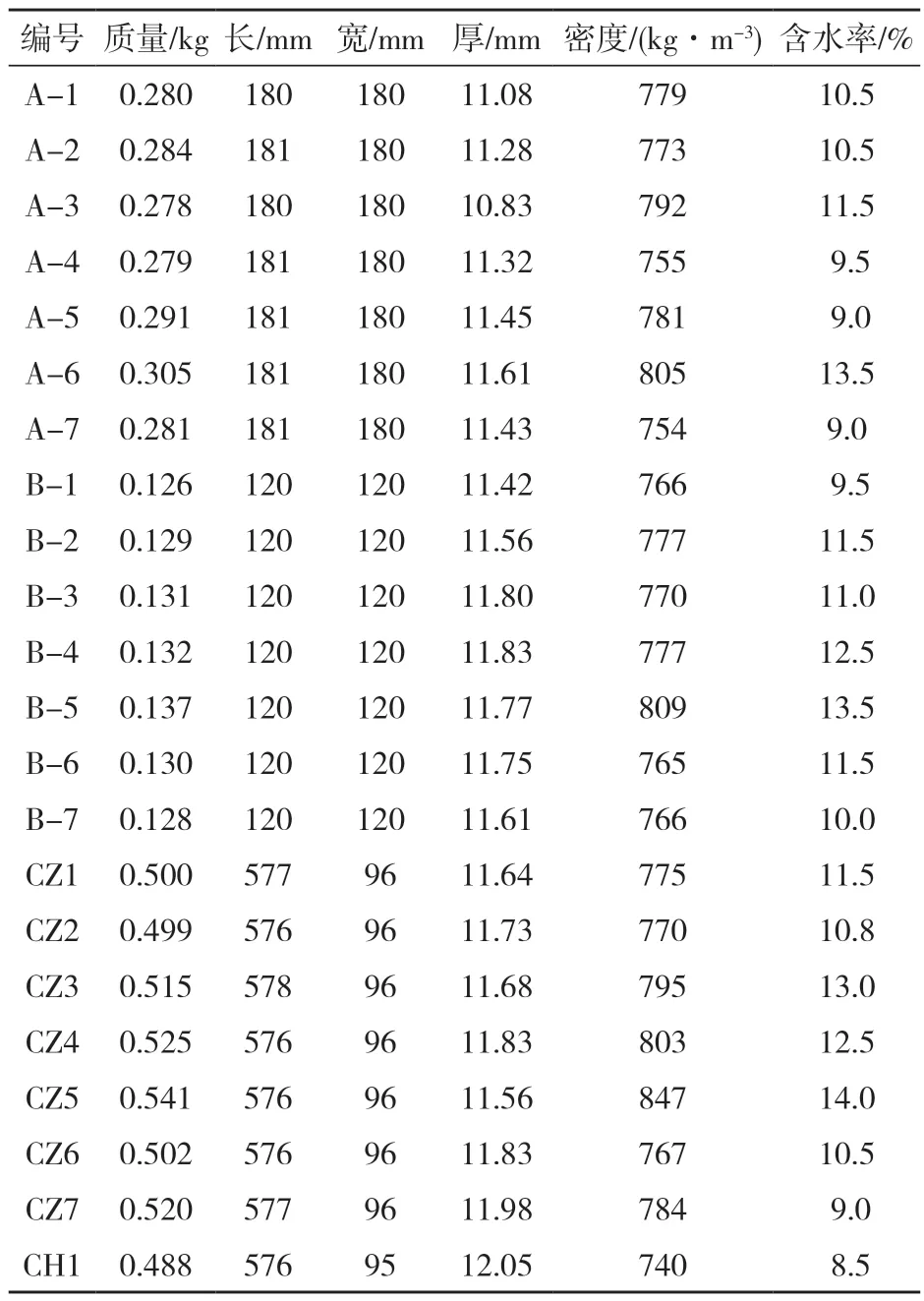
表1 竹胶合板试件参数Tab.1 Parameters of bamboo plywood sample
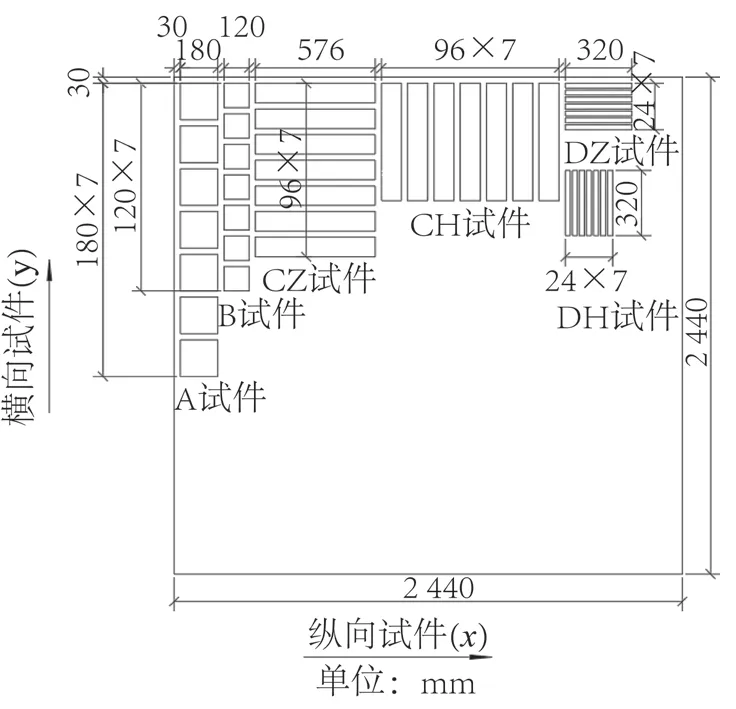
图2 竹胶合板试件下料图Fig.2 Blanking drawing of bamboo plywood test piece
1.2 测试方法与测试原理
1.2.1 自由板弹性模量和剪切模量动态测试
(1)自由板模态法测试
其测试原理为:在动态信号振动试验法基础上,根据板面节点图,划分为6*2 的网格,如图3。依次敲击竹胶合板板材,使其产生横向自由振动,产生的横向振动通过加速度计接受机械力信号并将其变为电信号,经信号调理仪进行信号放大、滤波等后,再通过结构模态分析软件MaCras的频谱识别、正交检验,最终得出竹胶合板试件的模态参数与振型。
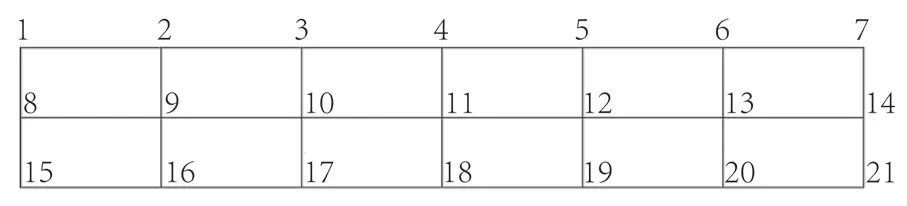
图3 网格划分图Fig.3 Gridding diagram
(2)自由板瞬态激励法测试
自由板瞬态激励法的弹性模量和剪切模量动态测试采用自由板瞬态激励法根据欧拉梁的横向弯曲理论[24],得到弹性模量值。其自由梁的一阶弯曲频率与弹性模量E的关系为:
式中:E为动态弹性模量值,Pa;ρ为气干密度,kg/m3;f1b为自由梁一阶弯曲频率值,Hz;l为梁长度,m;h为梁厚度,m。
采用自由板扭转振形法中自由板振形系数γ并借助悬臂板扭转模态法计算悬臂板振形系数C1和C2的原理,计算竹胶合板自由板振形系数,得到剪切模量G。
自由板一阶扭转频率与剪切模量的关系为:
式中:G为试件剪切模量,Pa;l为自由板长度,m;b为自由板宽度,m;h为自由板厚度,m;f1t为自由板一阶扭转频率,Hz;ρ为气干密度,kg/m3;γ为自由板振形系数;β≈
自由板振形系数γ采用公式[25]:
纵向:
相关系数r=0.999 98,n=6
横向:
相关系数r=0.999 98,n=6
其测试原理为:使用牛皮筋进行悬挂,实现自由梁约束方式,在板的角点固定加速度计连接CRAS振动及动态信号采集分析系统及其SsCras信号分析软件;通过锤击试件角点激励板自由振动,使得加速度计接收振动信号并转换为电信号输出,经过信号放大、滤波后,再经动态信号与采集分析系统软件SsCras处理得到试件频谱,从频谱上可读取试件一阶弯曲和一阶扭转频率[26-34];最后将其频率数值代入式(1)、式(2)计算得到竹胶合板的E、G,如图4所示。
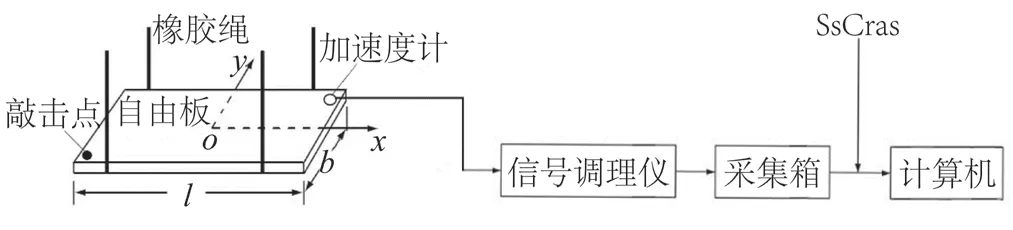
图4 自由板瞬态激励测试系统框图Fig.4 Block diagram of free plate transient excitation test system
1.2.2 方板扭转振型法的剪切模量动态测试
其测试原理为:以十字交叉的两根弹性绳悬挂方板。一根弹性绳沿方板的长度方向延伸,且位于方板宽度方向的中间位置,另一根弹性绳沿方板的宽度方向延伸,且位于方板长度方向的中间位置;加速度计安装于方板上表面沿长度方向距角点3/8l处;通过锤击方板上表面的角点处激励方板自由振动,使得加速度计接受振动信号并转换为电信号输出,再将电信号放大、滤波后经AD转换,从频谱上读取试件的一阶扭转频率ft,得到剪切模量值,如图5 所示。其方板一阶扭转频率与剪切模量G的关系为:
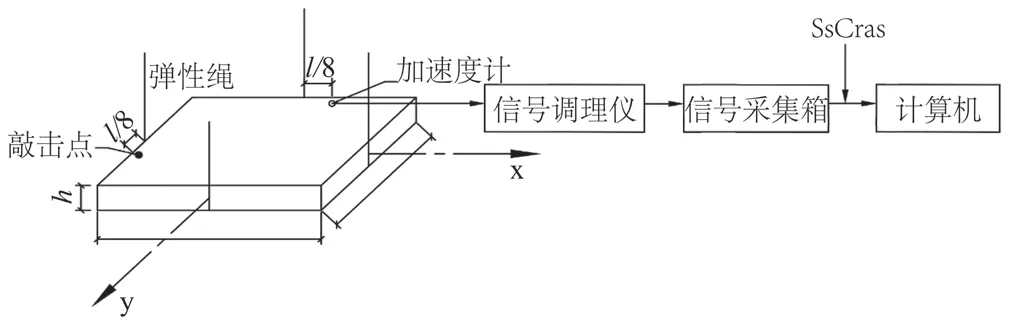
图5 方板扭转振型法测试系统框图Fig.5 Block diagram of square plate torsional mode method test system
式中:G为试件剪切模量,MPa;l为板长度,m;b为板宽度,m;h为板厚度,m;ft为自由方板一阶扭转频率,Hz;ρ为气干密度,kg/m3
2 竹帘竹胶合板弹性模量,剪切模量和泊松比的静态验证试验
2.1 对称四点弯曲梁法的弹性模量和泊松比静态验证试验
对称四点弯曲梁加载示意图和非对称加载四点弯曲梁试验装置示意图分别如图6和图7所示。
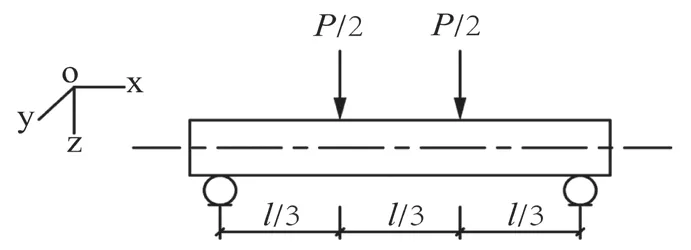
图6 对称四点弯曲梁加载示意图Fig.6 Schematic diagram of symmetrical four-point bending beam loading
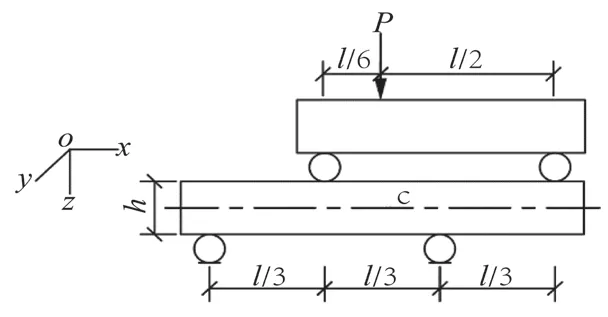
图7 非对称加载四点弯曲梁试验装置示意图Fig.7 Schematic diagram of four-point bending beam test device under asymmetric loading
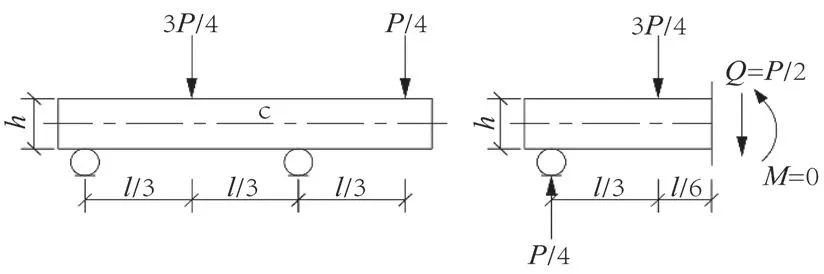
图8 非对称加载四点弯曲梁的受力图Fig.8 Stress diagram of four-point bending beam under asymmetric loading
其弹性模量E可表示为
式中:E为弹性模量,MPa;l为梁长度,mm;b为梁宽度,mm;h为梁厚度,mm;ΔP为载荷增量,N;Δεx为纵向应变增量,με。
在纯弯曲段的梁上下表面中心点的横向应变和纵向应变测试值若分别为εy和εx,则泊松比可表为:
式中:Δεx为纵向应变增量,με;Δεy为横向应变增量,με。
2.2 非对称四点弯曲梁法的剪切模量静态验证试验
非对称四点弯曲梁法测试木材剪切模量基于剪切胡克定律和矩形截面梁中性轴上点的最大剪应力计算公式,通过测量中性轴上点的剪应变推算出剪切模量。
其剪切模量G可表为,写成便于测试的增量形式
式中:G为剪切模量,MPa;b为梁宽度,mm;h为梁厚度,mm;ΔP为载荷增量,N;Δε-45°和Δε45°分别为梁侧面中心点的负45°和正45°方向的线|Δε-45°-Δε45°|=2ε读数应变,με。
3 结果与分析
3.1 竹帘竹胶合板自由板弹性模量和剪切模量的动态测试
3.1.1 自由板试件
试验选取CZ-1和CH-1进行测试,初步确定了竹胶合板试件的一阶弯曲频率与一阶扭转频率区间,如图9和图10所示。由图可知,自由状态下CZ-1一阶弯曲频率为106.5 Hz,一阶扭转频率为266.7 Hz。
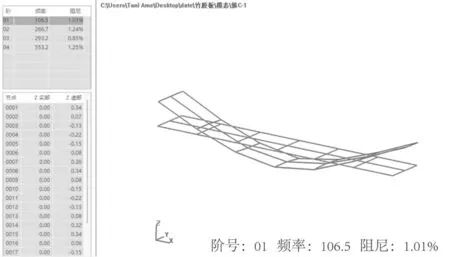
图9 CZ-1 一阶弯曲模态Fig.9 CZ-1 first-order bending mode
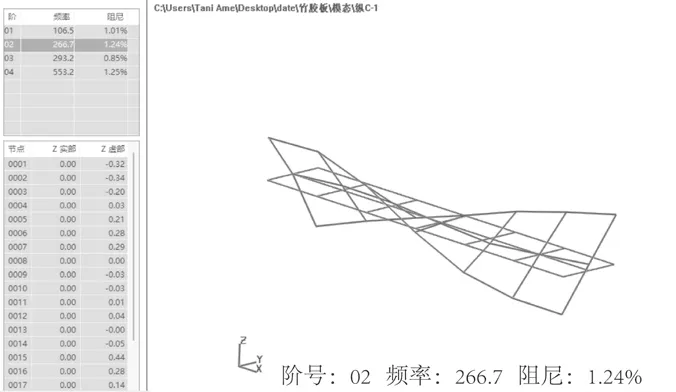
图10 CZ-1 一阶扭转模态Fig.10 CZ-1 first-order torsional mode
图11为 CZ-1自由板试件频谱。从图中可以看出,该试件的一阶弯曲频率为106.3 Hz,一阶扭转频率为265.0 Hz,与悬挂模态测得频率基本一致。表2为自由板模态测试和瞬态测试的结果,其误差在2%以内,充分证明了瞬态测试的准确性。
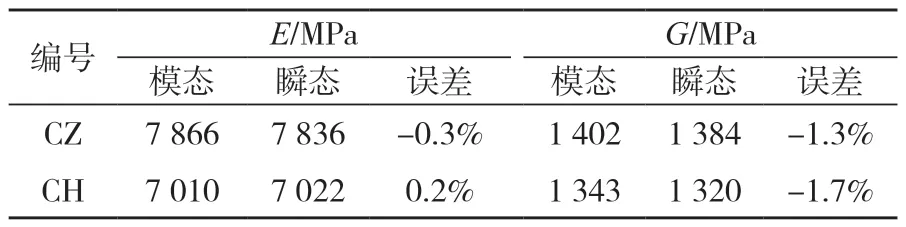
表2 自由板模态与瞬态测试结果Tab.2 Free plate modal and transient test results
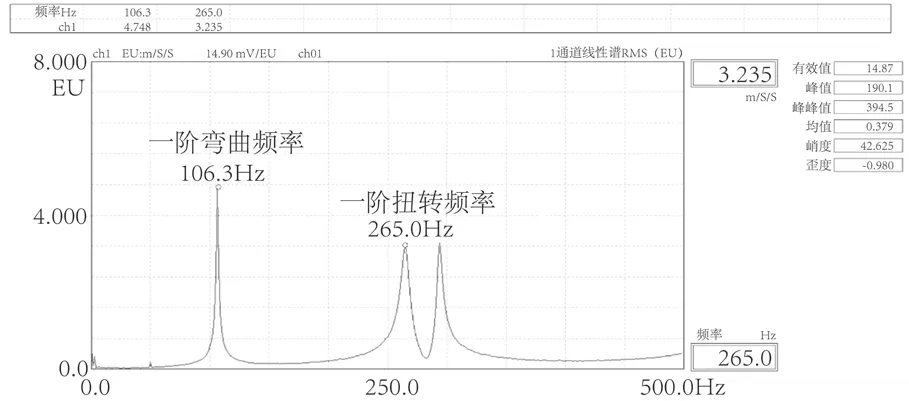
图11 CZ-1 频谱图Fig.11 CZ-1 spectrum diagram
通过瞬态试验测得,CZ试件的平均弹性模量为7 836 MPa (COV:9%)、剪切模量为1 384 MPa (COV:4.31%);CH试件的平均弹性模量为7 022 MPa (COV:9.8%)、剪切模量为1 320 MPa (COV:4.31%)。根据结果可知,该种竹胶合板的弹性模量变异性较大,可能与制造工艺水平和原材料有关。横向板平均弹性模量比纵向板的平均弹性模量小10.3%,横向板平均剪切模量比纵向板的平均剪切模量小4.6%,而平均一阶弯曲频率和平均一阶扭转频率基本一致。
竹胶合板为7层正交结构,外侧附加薄木装饰层,热压前除中心层为2.5 mm厚外,其余层均为1.8 mm厚(薄木除外)。但此结构决定横向板的纵向层厚度为7.2 mm,纵向板的纵向层厚度为6.1 mm,均为热压前厚度。由于竹材为维管束结构,且竹片具有一定弧度,在热压后会出现一定的收缩,其压缩率约为15.6%,因而进一步缩小了横向板与纵向板的厚度差异。由于原材料竹胶合板的基本单元竹片,在尺寸较长的情况下难以保证厚度一致,导致部分板材出现纵向层加厚现象或横向层加厚导致纵向层变薄的现象,如图12(a)和(b)所示,在测试中直接体现在了板材一阶弯曲频率上,显著提升了弹性模量。
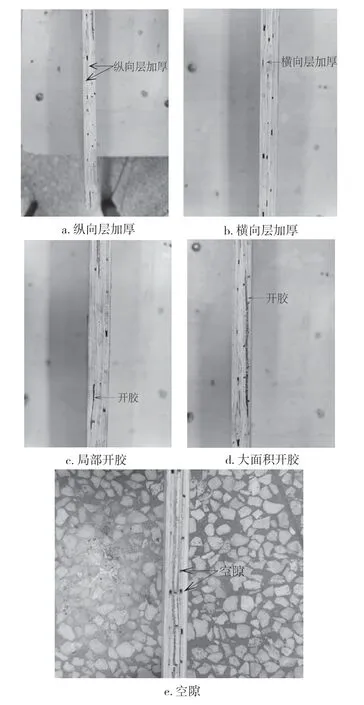
图12 竹胶合板材料与工艺缺陷Fig.12 Material and process defects of bamboo plywood
部分板材出现了开胶和漏胶现象,其主要出现在CH试件上,如图12(c)和12(d)所示,这直接影响了板材的内结合强度,降低了板材的弹性模量。这是由于该竹胶合板原料主要选择靠近竹青的最外侧竹黄,工艺水平不佳导致基材竹片上留有部分竹青组织,而竹青主要成分为硅质细胞,硅成分影响了胶黏剂的渗透,最终导致部分位置开胶。
此外,由于工艺原因,板材上存在肉眼可见的孔洞空隙,如图12(e)。这些空隙直接导致板材空隙率的上升和密度的下降,使得CH试件的平均密度比CZ试件高6.2%。由此可见,竹胶合板密度对其弹性模量和剪切模量的影响较大。
由于剪切模量是反映材料某一面内性能的弹性常数,在本试验中测得的剪切模量均为xy面的剪切模量,因此与试件长度方向无关,而结果也证实,影响横向板与纵向板剪切模量的唯一因素是板材的密度。其xy面内扭转剪切模量能达到1 300 MPa以上,具有较好的抗扭转能力,适合用于车厢底板。
3.1.2 梁试件
为了验证该材料是否具有位置效应并方便静态验证,在原整板其他位置,裁剪出纵梁试件DZ和横梁试件DH,经计算,纵向梁和横向梁的平均弹性模量分别为6 565 MPa (COV:6.4%)和7 565 MPa (COV:8.0%),其横向梁弹性模量比纵向梁的弹性模量大15.2%,横向梁一阶弯曲频率比纵向梁的一阶弯曲频率大11.6%。
由表3得知,梁试件的密度影响弹性模量值的大小。同向梁试件的密度越大、其空隙越小,弹性模量越大。
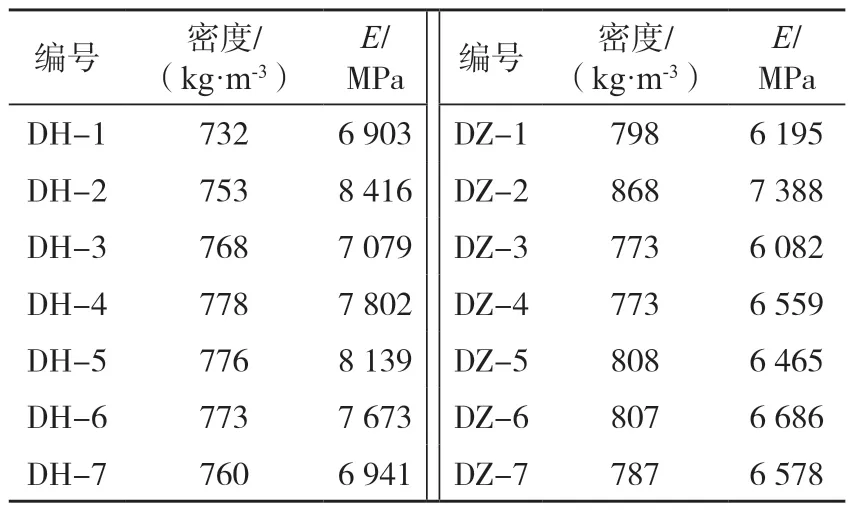
表3 梁试件密度与弹性模量对照表Tab.3 Comparison table of beam specimen density and elastic modulus
3.2 方板扭转振型法的剪切模量动态测试
为研究该竹胶合板是否受尺寸效应影响,采用长宽比为1 的方板与长宽比为6 的矩形板进行对比。方板测试其剪切模量,采用2 种规格的方板,即A和B两种试件,进行方板扭转振型法测试。
代入式(5)计算,得到各方板试件的剪切模量。长宽为180 mm的A方板平均剪切模量为1 424 MPa(COV:4.5%),长宽为120 mm的B方板平均剪切模量为1 381 MPa (COV:6.9%)。方板A剪切模量比方板B剪切模量大3.1%,其结果与矩形板自由悬挂瞬态激励测试的结果基本吻合。
3.3 弹性模量,剪切模量和泊松比的静态验证试验
考虑到该竹胶合板本身均匀性较差,且竹材作为天然材料,外层靠近竹青和内层靠近竹黄,这两侧细胞组织存在一定的结构差异,测试时为了区分试件的上下表面,定义花纹面为P面,木纹面为N面,进行上P下N,上N下P两组测试,如图1所示。
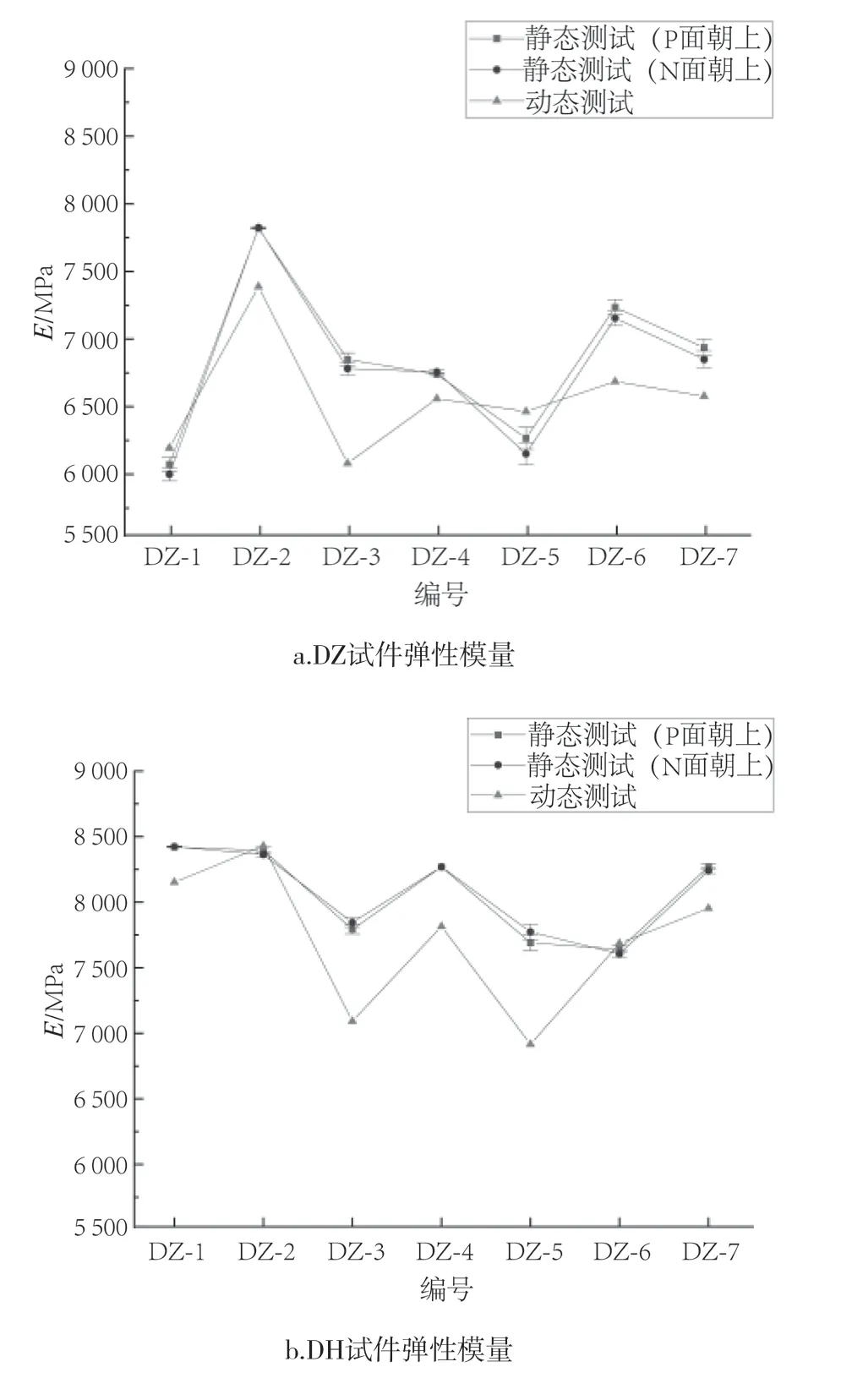
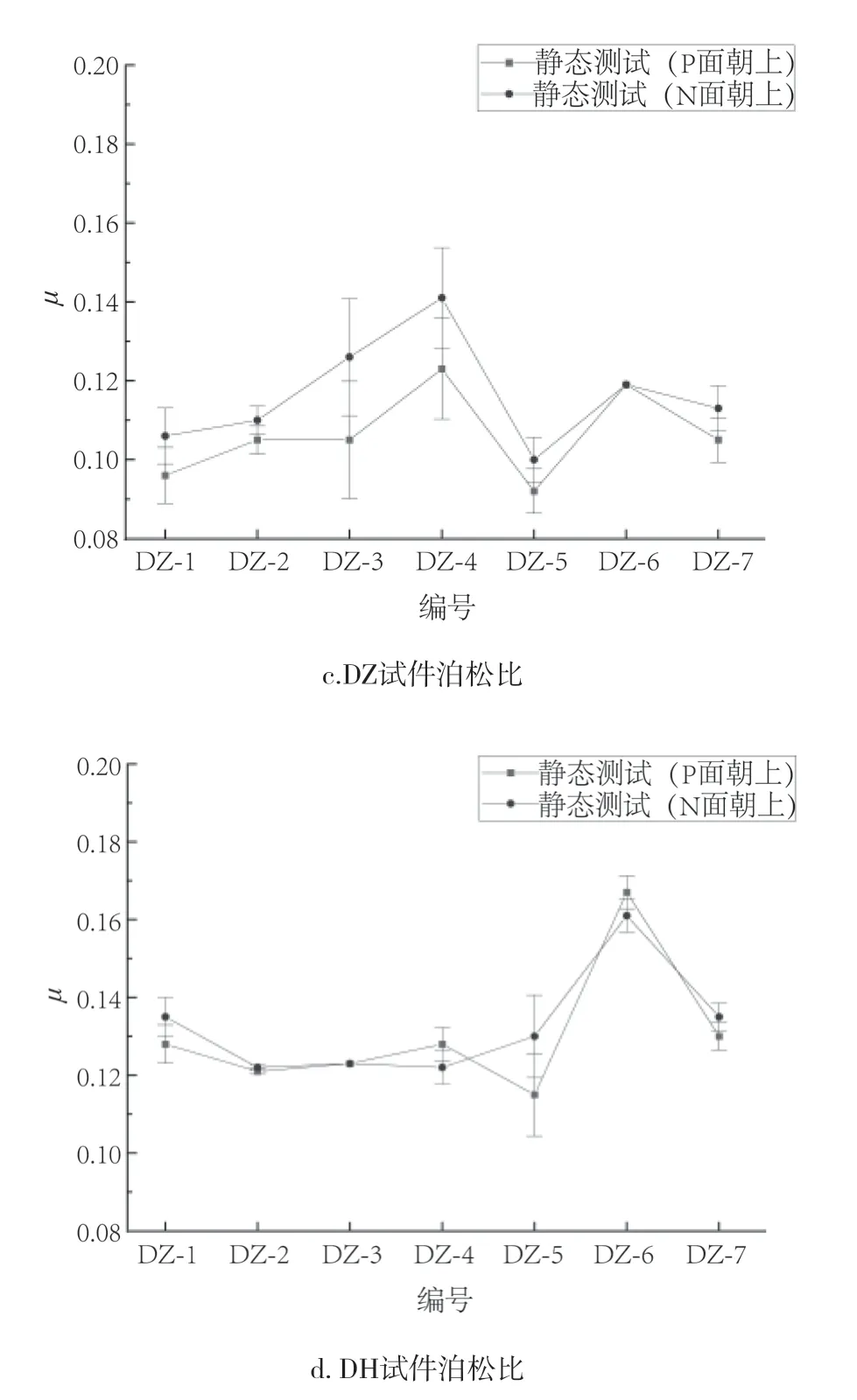
图13 静态对称四点弯曲试验结果汇总Fig.13 Summary of static symmetric four point bend test results
由图可知,梁试件由对称四点弯试验测得沿整板长度方向弹性模量Ex均值为6 817 MPa,沿整板宽度方向弹性模量Ey均值为8 059 MPa。纵梁弹性模量比横梁弹性模量小15.4%,纵梁泊松比比横梁泊松比小15.1%。翻转试件上下表面对测试结果基本无影响。Ex、Ey测试值的变异系数均小于2%,证实了测试的可靠性。
梁试件由非对称四点弯试验测得的Gxy均值为1 298 MPa,Gyx均值为1 370 MPa,两者均为xy平面内剪切模量,测试结果仅相差5.3%。Gxy、Gyx测试值的变异系数均小于2.5%,证实了测试的可靠性。
3.4 竹胶合板E, G, μ动态测试和静态验证试验的对比
综合梁试件的动态测试与静态测试结果见表4~5。
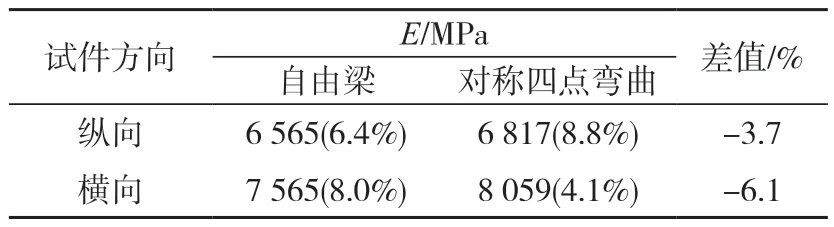
表4 梁试件动静态E测试结果Tab.4 Dynamic and static E test results of beam specimen

表5 板、梁试件动静态G测试结果Tab.5 Dynamic and static G test results of plate and beam specimens
由表4 可知,纵向梁试件动态弹性模量比静态弹性模量小3.7%,横向梁试件动态弹性模量比静态弹性模量小6.1%,可认定动态自由悬挂瞬态激励测试的准确性。各试验对纵横两向弹性模量值的测试偏差相近,证实了各试验的可靠性。静态纵梁弹性模量比横梁弹性模量小15.4%,与动态梁弹性模量比横梁弹性模量小15.2%极为接近。将静态测得的E、G、μ代入G=E/2(1+μ)的关系式,发现其不成立,可见本竹帘竹胶合板为各向异性材料,且各试验对纵横两向弹性模量值的测试偏差相近,证实了动态试验的可靠性。
自由悬挂纵向板剪切模量分别比非对称纵向梁和横向梁小6.7%和1.3%。自由方板A的剪切模量分别比非对称四点弯纵梁和横梁的剪切模量大9.8%和4.0%。自由方板B的剪切模量分别比非对称四点弯纵梁和横梁的剪切模量大6.5%和0.8%。纵向与横向剪切模量均为xy平面内的剪切模量,两者测试结果相近,且动静态测试结果的偏差均在10%以内,证实了动态测试结果的可靠性。
4 结论
1)利用自由板瞬态激励法测试的竹帘竹胶合板弹性模量和剪切模量与其模态试验结果一致。动态测试竹帘竹胶合板弹性模量、剪切模量和泊松比均值分别为0.7 GPa、1 300 MPa和0.12,均符合GB/T 13123—1991 和LY/T 1575—2000 中一等品规定要求。
2)竹帘竹胶合板不满足G=E/2(1+μ)关系,为各向异性材料,其横向与纵向的弹性模量之比为1∶1.15,纵向与横向剪切模量之比为1∶0.95。
3)动静态法测得竹胶合板梁试件的弹性常数误差小于7%,且动态测试弹性常数的变异系数小,说明动态测试具有准确度高和可靠性好的特点。
4)测试的竹帘竹胶合板差异性较大,主要与其生产工艺精度不高,且生产原料的均质性差有关。
5)方板试件测试方法更接近于原整板的使用环境。静态法测试剪切模量操作复杂,速度慢,方板扭转振形法更适合采用动态法,且具有快捷、简便、准确性高等优点。

