依“葫芦”画非二次函数的图象给研究函数带来便利

谭德锡

【摘  要】  “形”与“数”之间的相互转化在解决数学问题中是常见的，数形结合思想是数与形间的对应关系，是通过数与形的相互转化来解决数学问题的思想.由“形”到“数”的转化往往较明显，而由数到形却需要较强的思想意识，用数形结合思想解决数学问题往往是将较为抽象的问題化为容易理解的形，再由形描述需要的数.二次函数图象在中学阶段具有非凡意义，为画其他函数的图象提供导航作用.

【关键词】  函数图象；单调性；最值；极值

众所周知，数形结合思想在解决数学问题起着非常重要的作用，函数图象为解决函数问题提供了直观性.由直观想象到数学抽象再到逻辑推理的过程函数图象都起着穿针引线的作用.二次函数图象在中学阶段具有标志性意义，它能给画非二次函数型函数图象提供导航的作用，从而给讨论函数单调性、求函数的最值、极值等提供了快速、便捷的作用.

用二次函数作导航，巧画非二次函数的图象，再讨论函数单调性、求函数最值和极值的例子举不胜举，在模拟考试和高考中都考过，是高考中的常客.

结语

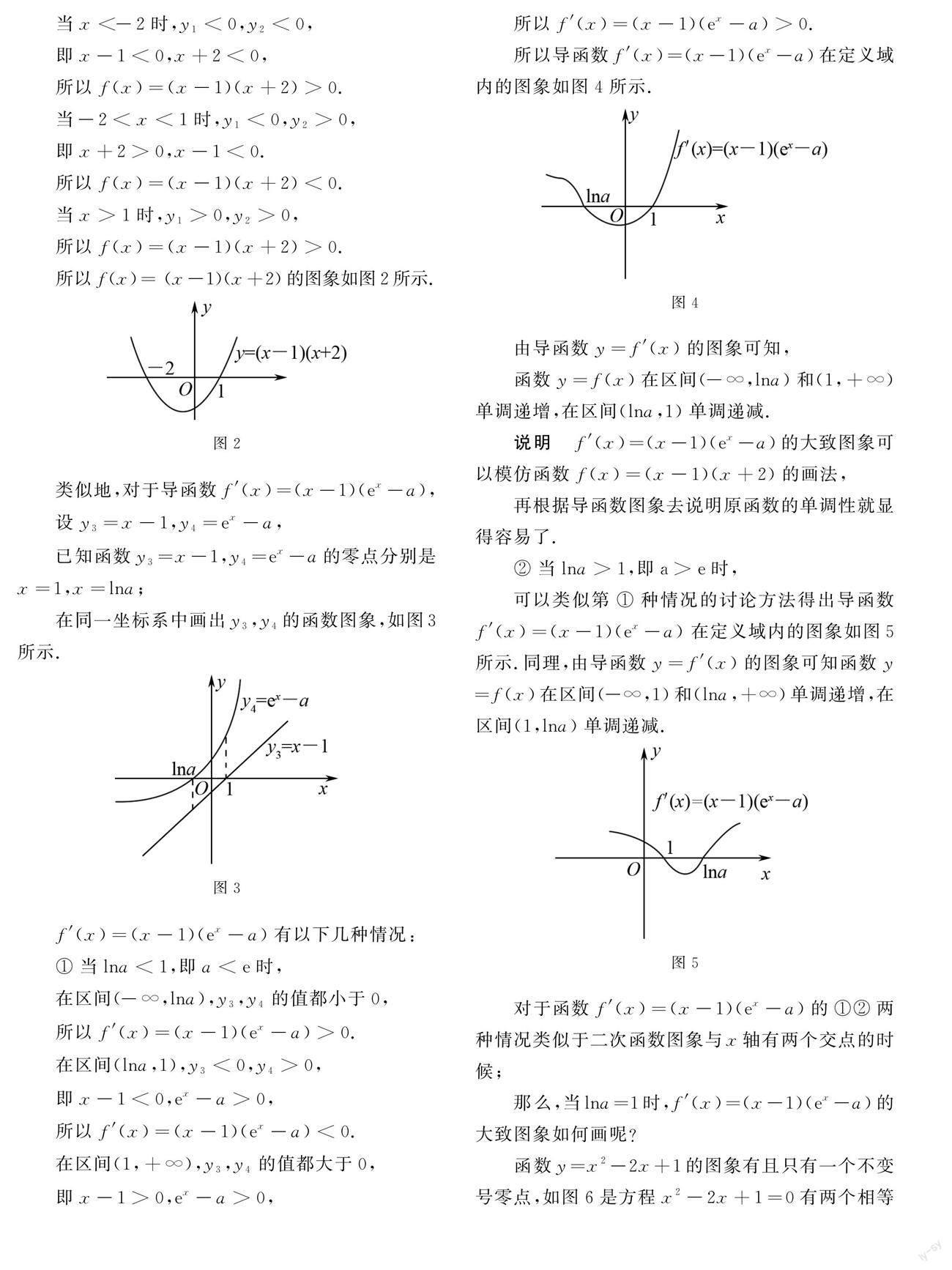
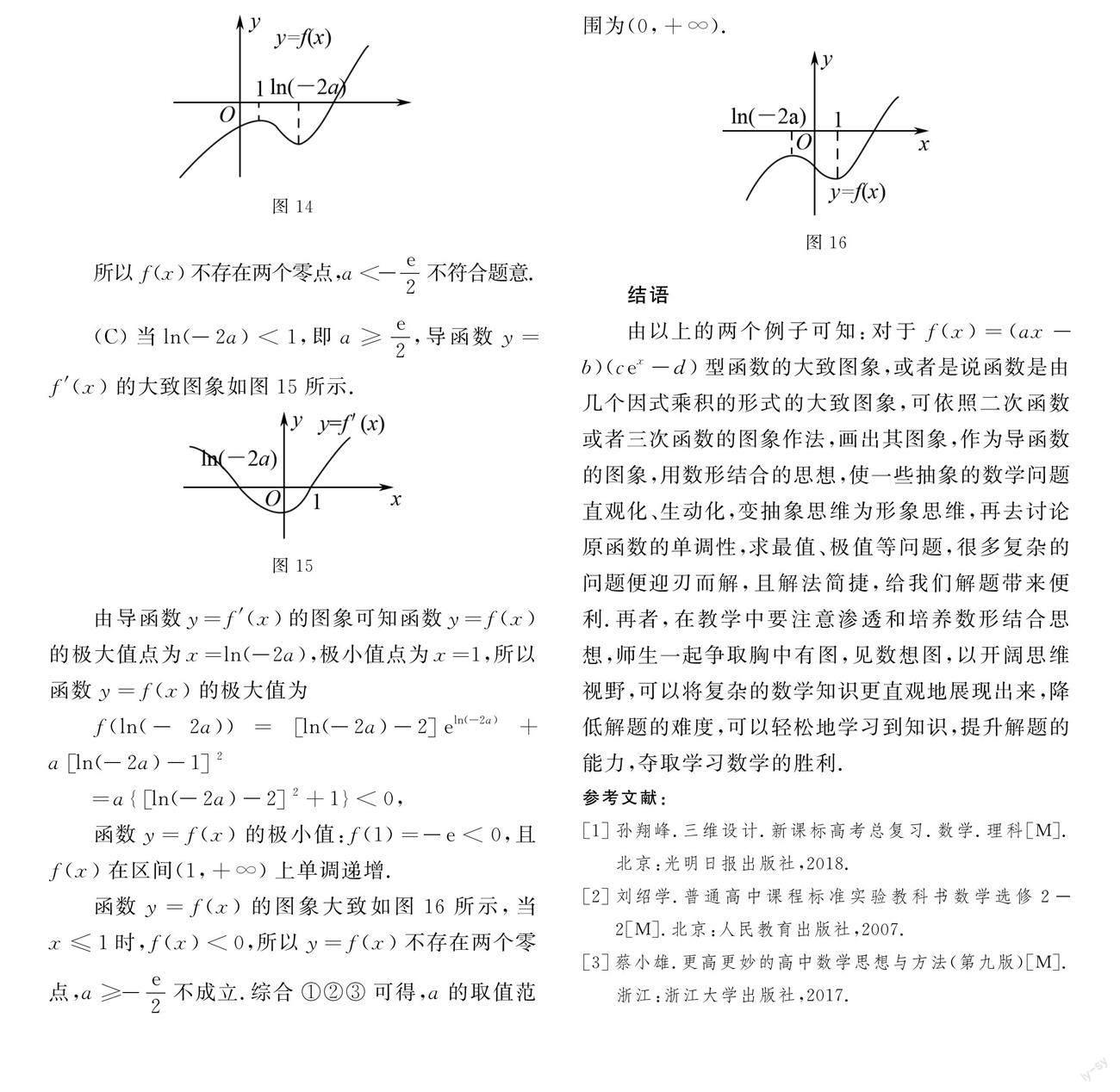
由以上的两个例子可知：对于点击并拖拽以移动型函数大致图象，或者是说函数是由几个因式乘积的形式的大致图象，可依照二次函数或者三次函数的图象作法，画出其图象，作为导函数的图象，用数形结合的思想，使一些抽象的数学问题直观化、生动化，变抽象思维为形象思维，再去讨论原函数的单调性，求最值、极值等问题，很多复杂的问题便迎刃而解，且解法简捷，给我们解题带来便利.再者，在教学中要注意渗透和培养数形结合思想，师生一起争取胸中有图，见数想图，以开阔思维视野，可以将复杂的数学知识更直观地展现出来，降低解题的难度，可以轻松地学习到知识，提升解题的能力，夺取学习数学的胜利.

参考文献：

[1]孙翔峰.三维设计.新课标高考总复习.数学.理科[M].北京：光明日报出版社，2018.

[2]刘绍学.普通高中课程标准实验教科书数学选修2-2[M].北京：人民教育出版社，2007.

[3]蔡小雄.更高更妙的高中数学思想与方法（第九版）[M].浙江：浙江大学出版社，2017.