“深度学习”理念下高中数学教学模式初探*

无锡市立人高级中学 徐 科

1 深度学习的理解

20世纪中后期,国外学者对深度学习(Deep Learning)展开了研究.21世纪,国内也有很多学者对“深度学习”展开了研究.阎乃胜教授指出: “深度学习”是指对信息予以深度加工,深刻理解和掌握复杂概念的内在含义,建构起个人情景化的知识体系,以知识迁移推进现实任务的完成.黎加厚等也在《促进学生深度学习》(2005)一文中明确了深度学习的定义.深度学习是指学习者在理解学习的基础上,批判性地学习新的思想和事实,将它们纳入原有的认知结构中,并且能够联系不同的思想,将已有的知识迁移到新的情境中,作出决策和解决问题.综合学者对“深度学习”的定义,可以得到如下理解:

(1)深度学习是相对于浅层学习的一个概念,深度学习不是简单的知识灌输或者是学会一些固定的方法与技巧,而是对信息进行整合,对知识的构成进行内化.

(2)深度学习并不是针对一个知识点的孤立学习.深度学习必须有一个体系化的过程,从原有的知识中构建知识体系,并对新的信息进行处理使之纳入到以后的知识体系中,并向外延伸.

(3)深度学习的最终目标是知识的迁移,或者说是应用.无论是知识、技能、方法、还是理念、思想,只有进行应用才能体现其价值.

2 深度学习教学模式初探

2.1设置认知冲突,引导主动学习

认知心理学家认为:当学习者发现不能用已有的知识来解释一个新问题或发现新知识与已有的知识相悖时,就会产生认知失衡.为了重新保持平衡,这种认知冲突就会激发学习者的探索意愿,而这正是促进深度学习、发展高阶思维的最佳时期.

教学片断等比数列前n项和公式的推导

师:如何求一个等比数列的前n项和呢?对于一般形式Sn=a1+a1q+a1q2+……+a1qn-1,我们会感到困难,那我们可以选择一个简单的等比数列开始研究.你会选择哪个数列来求和呢?

生:选择1+22+23+……+2n-1.

师:用什么方法来求1+22+23+……+2n-1?

师:可以考虑一下以前学过的一些数列求和方法.

生:倒序相加求和法.

师:尝试一下,看能不能倒序相加?

生:不行.

师:为什么?

生:因为等比数列没有am+an=ap+aq(m+n=p+q,m,n,p,q∈N*)

师:有没有其他求和方法呢?

生:可以尝试一下累加法或者累乘法.

通过板演发现,累加、累乘都不能解决问题.

师:通过上述方法的尝试,大家有没有领悟到,解答数列求和问题的一个基本方法?

生:……

师:数列求和问题让人最困惑的是什么?

生:项数n,n代表很多,但又不确定是多少,从而产生计算困难.

师:以往学习的数列求和方法在数列求和中都能起什么作用呢?

生:是让n变成“可运算”.

师:就是把“无限”变成“有限”.那对于Sn=1+22+23+……+2n-1,我们有什么办法把n项变成“有限项”呢?

生:……

师:可以从等比数列的定义形式入手,请大家尝试一下.

…………

教学反思：在“等比数列前n项和公式的推导”教学过程中,学生不像学习“等差数列前n项和公式的推导”一样有很好的知识储备,根据“高斯求和”,能够摸索出倒序相加求和法,这就导致了“认知失衡”.而教材中(新人教A版选择性必修第二册第35页)的一段引入“我们发现,如果用公比q乘①的两边,可得……”给人的感觉是强硬地给出了乘公比错位相减,而并非通过学生的主动学习得到.在上述教学过程中,通过问题引导学生尝试已有的方法来求解,虽然不成功,但是这个过程强化了学生的主动探究,比直接引出“乘公比错位相减”的教学过程更具深度.

2.2新旧知识整合,构建知识体系

碎片化的知识,给学生的记忆带来了困难,一方面遗忘率高,另一方面知识运用效率低下.在新授课中如果能整合新旧知识,形成知识体系,就能够促进学生知识的分化和泛化,加深学生对新知的理解.知识体系的构成过程实际上也培养了学生思维的逻辑性与严谨性.

教学片断平面与平面平行

师:学完了平面与平面平行的判定定理与性质定理,我们能不能和前面所学的知识比较一下,看看它们有何联系?

生1:根据刚刚所学知识,要证面面平行就要找两条直线与平面平行,当然两条直线要相交;要证线面平行就要找(平面外)一条线与平面内的一条线平行.

生2:它们的联系是线线平行可以推出线面平行,线面平行可以推出面面平行,但是线线平行不能直接推出面面平行(易错点).

生3:面面平行的可以推出线面平行,也可以推出线线平行.

生4:线面平行可以推出线线平行.

生5:直线与平面平行的判定与性质都是“三推一”,两个平面平行的判定是“五推一”,两个平面平行的性质也是“三推一”

师:不要局限于平行之间的联系,我们还可以想一下垂直.

生6:如果两条直线垂直于同一个平面,那么这两条直线平行.

生7:如果一条直线垂直于两个平面,那么这两个平面平行.

师:很好,大家各抒己见说了很多,由于时间关系,请同学们课后做一张图表,梳理立体几何中我们已经学过的平行知识.

学生梳理的立体几何中的平行关系如图1所示.

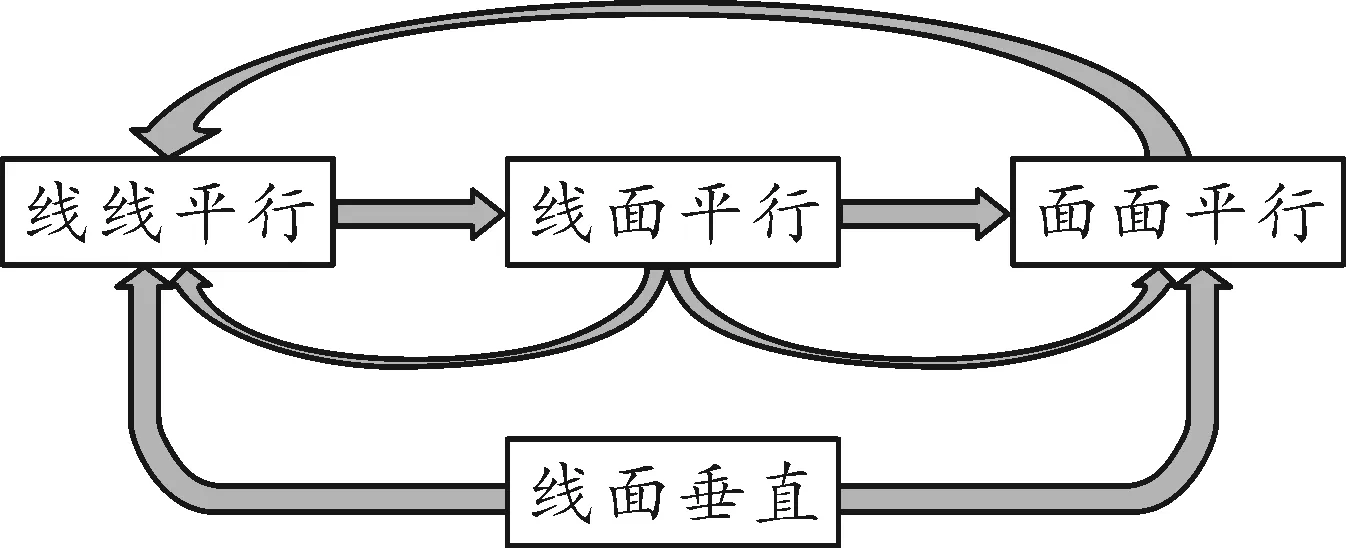
图1

教学反思：上述环节看似有点脱离新课“平面与平面平行”的教学主题,有点复习课的味道,但通过3～5分钟的知识回忆,把新授知识整合进原有知识中去,并形成原始的知识体系.随着理解的深入和所掌握知识的丰富,知识体系将变得更为丰满,这样就把原本较为单一的一个个知识点,变成小知识体系,融入自己的知识储备中.

2.3强化知识应用,构建深度思维

深度学习的最终目的是知识的迁移,为了达成这个目的,教师应该在课堂上树立“学以致用”的教学理念.一方面在课堂上所学的新知识、新方法、新技能可以解决一般数学问题,另一方面也应该重视用数学方法去解决实际问题.

教学案例统计教学部分的“实习作业”

教材(苏教版必修三第81页)上布置了一个实习作业:自己(或分组)选择适当的课题,进行统计研究,并写出报告.

根据这一选题,教师提出问题:我们常说数学学习好的同学物理学习也好,学完统计这部分内容知识,大家能否对本班同学的成绩进行统计分析,得到你自己的判断.

学生分组之后就进入实践.首先是数据的获取.有些小组的学生采用的是部分同学的中考数学成绩与物理成绩,原因是中考分数的有效性(效度)较高;也有些小组的学生采用的是高一第一学期的期末成绩或者是第一学期期中与期末成绩的平均值,原因是中考代表的是过去,但高中学习与初中学习差异很大,所以应该采用高中的成绩.其次是选择数据处理模型.大部分小组采用线性回归的方式进行研究,但是从这里学生就开始出现问题.一是书本的内容是求出线性回归方程,这和数学成绩与物理成绩是否相关好像并不是一个问题;如果问题是“通过数学成绩来预测物理成绩”,那线性回归方程就有价值了.二是数据量很大,大部分小组是把全班同学的数据作为整体样本,但是班级人数在四十人左右,这样的计算难度太大了.

实际上,数据处理环节的两个问题,是学生进行深度学习的一个很好的机会.教材第80页的链接部分介绍了相关系数的概念,可以通过相关系数r来判断两组数据是否具有相关性.教材第77页中指出,处理数据可利用Excel进行数据拟合.

教学反思：实习作业作为一个很好的教学内容,在教学过程中应该有更多的体现.实习作业的设计意图,不应该仅仅停留在激发学生学习兴趣,让学生体会数学应用的价值等这些表层的内容上,更应该让学生能够更好地完善自我知识体系,从自我知识体系中迁移出新知识,从而进行真正的“深度学习”.

真正做好“深度学习”,一堂课或者是一小段时间的教学是不够的,但是在长期的教学过程中让学生树立整合知识、构建知识、运用知识的理念,就能让学生得到全面、可持续的发展.