一道高考参数方程题的解法分析及教学反思

海南省昌江黎族自治县昌江中学 林瑞记

知过去,才能谋未来.我们的高中生从来都不缺乏练习题、高考题的训炼,但大多都浅尝辄止,缺乏上下求索的学习态度,导致各个数学知识点之间的联系没有得到很好的构建,知识的外延也没能得到很好的拓展.实际上,很多高考题具有很强的教学意义和研究价值.笔者曾参与海南省2018年高考阅卷工作,现试着从2018年全国Ⅱ卷第22题关于参数方程问题的研究出发,剖析该参数方程题的不同解法,归纳解该类题目的思想方法.首先介绍考生的常见解题思路,并分析不同考生解法的思维特点,然后进一步研究不同的解法,最后揭示不同数学思维水平的考生该如何在考场中“扬长避短”,以及教师在教学中如何做到“因材施教”,落实新课标提出的高中数学学科六大核心素养[1].

1 试题呈现

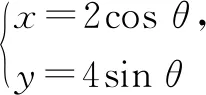
(1)求C和l的直角坐标方程;

(2)若曲线C截直线l所得线段中点的坐标为(1,2),求l的斜率.

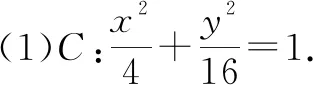
当cosα≠0时,l:y=tanα·x+2-tanα;当cosα=0时,l:x=1.(2)直线l的斜率为-2.

2 参数方程问题的解题策略分析

该题在高考中属于选考题,因为其主要考查的内容是三角函数和解析几何,属学生较为熟悉的知识点,故而在高考考场上选择的考生颇多.第(1)问主要考查学生将极坐标方程转化为直角坐标方程、参数方程转化为普通方程的能力,尽管该问较为简单,但是直线l的转换出错较多.对于第(2)问,学生的解法主要是将直线l的参数方程代入曲线C的直角坐标方程中去求解,思维的切入点不同,解题的方法往往就大相径庭[2].

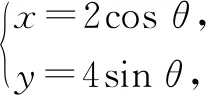
当cosα≠0时,直线l的直角坐标方程为y=tanα·x+2-tanα;当cosα=0时,直线l的直角坐标方程为x=1.

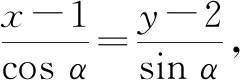
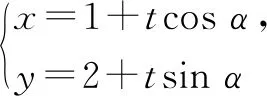
(1+3cos2α)t2+4(2cosα+sinα)t-8=0.

①

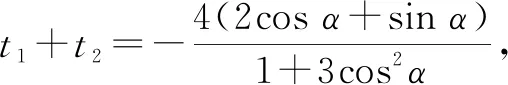
具体策略分析：解法1在阅卷中属于司空见惯的,由于其解题思路清晰及步骤操作偏模式化,因此有很多考生青睐这种解法,也体现了这类考生数学运算素养较强.因此,在教学中针对这类学生,教师应当着重加强计算能力和运算技巧的训练,这样才能做到有的放矢地教学,这应该也算是数学学科的“因材施教”吧!

解法2：(ⅰ)当cosα=0时,曲线C截直线l所得线段的中点为(1,0),不合题意.

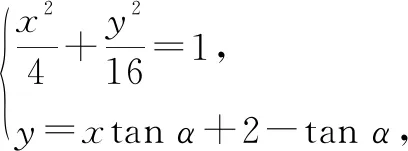
整理得(4+tan2α)x2+2tanα(2-tanα)x+tan2α-4tanα-12=0.

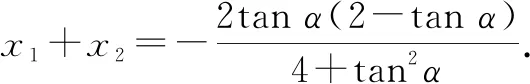
故直线l的斜率为-2.

具体策略分析：解法2较之解法1,在思维上走的弯路较少,联立后整理得到的方程的解本身就是题目所求,没必要牵涉到参数t的含义,所以考场上运用解法2的考生也较多.但是,很多学生运用该解法总是拿不到满分,原因是没有考虑cosα=0的情况,即直线l的斜率不存在的情况.针对这类学生,课堂上教师应该有意识地培养他们的数学抽象素养.

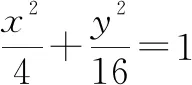
具体策略分析：解法3是常用于解圆锥曲线问题的点差法,思想就是未知参量设而不求,最后直接整理得斜率的表达式并求解.考场上运用该解法的学生思路清晰,基本都能拿满分,不过也有部分学生忽略了x1=x2时斜率不存在的情况,导致被扣两分.从侧面来看,用解法3还出错的学生表现出其逻辑推理及直观想象素养不够强,教师在教学中应当见微知著,有目的地补齐这类学生的短板.

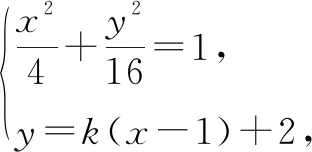
(ⅱ)当直线l垂直于x轴,即直线l的斜率不存在时,曲线C截得直线l所得线段的中点坐标为(1,0),不符合题意.

具体策略分析：解法4与解法2有着异曲同工之妙,都是将两方程联立并整理,再应用韦达定理和线段的中点坐标求解.这类解法在考场上较为罕见,主要原因是设直线方程再联立求解,其中的运算量较大,很多考生都望而却步.因此,在日常教学中,教师要有意识地强化学生的数学运算素养,只有夯实基础才能更上一层楼.

解法5：如图1,曲线C是中心在原点、焦点在y轴上、长轴长2a=8、短轴长2b=4的椭圆,上顶点为A(0,4),右顶点为B(2,0),线段AB的中点为(1,2),所以直线AB满足题目要求.故直线l的斜率为-2.

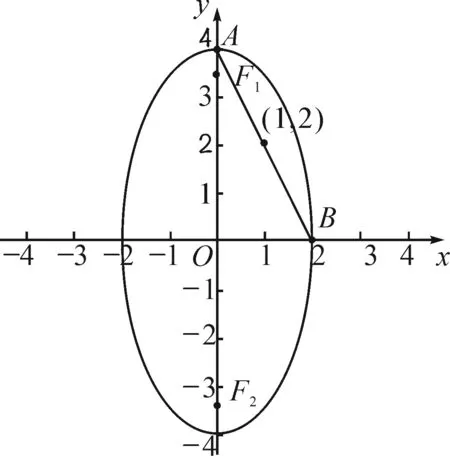
图1

具体策略分析：解法5鲜为考生所知,能用该法解决第(2)问的考生体现了其较强的数学抽象和直观想象素养,在争分夺秒的高考考场上思维仍能做到简明扼要、抽丝剥茧,的确令人激赏.

总之,参数方程问题的求解不仅要掌握参数方程中参数的含义,有时还需运用数形结合思想来思考和解答问题.通过这道参数方程题来审视我们的教学效果,确实还有很多需要改进的地方,很多素养需要加强.教师只有终身学习才能站好三尺讲台的岗,对以往高考题解法的回顾,能让思维得到锻炼和发散,能厘清知识间千丝万缕的联系.作为人民教师的我们,应生命不息教与学不止.