从四个维度对课堂进行评价 提升素养*——以立体几何轨迹问题教学为例

厦门外国语学校石狮分校 吴志峰

课标指出,高中数学教学要以发展学生数学学科核心素养为导向,启发学生思考,掌握数学内容的本质,落实数学核心素养的形成与发展.课堂学习评价有利于教师进行反思,改进教学,提高学生学习的兴趣.判断一节课是否能达到课标的学业水平要求,笔者认为可以从知识技能、思想方法、核心素养和关键能力四个维度进行评价.笔者结合自身教学实践,以“立体几何轨迹问题”教学为例,对课堂进行学习评价.

1 拟定课堂评价标准

为了落实课标所提出的学业水平要求,根据课标要求从四个维度拟定本节课的课堂评价标准:

知识技能:(1)关注学生运用图形概念描述图形的基本关系和基本结果,及常见曲线的轨迹定义,评价学生对轨迹的认知水平;

(2)关注学生能否运用定义法或坐标法求轨迹,评价学生对立体几何轨迹的运用水平.

思想方法:(1)关注学生能否借助图形寻找几何元素与数量之间的关系,评价数形结合思想的理解水平;

(2)关注学生能否将空间问题转化为平面问题,评价转化与化归思想的理解水平.

核心素养:(1)关注学生能否借助图形寻找几何元素与数量之间的关系,评价直观想象、数学建模与数学抽象素养;

(2)关注学生表述立体几何轨迹问题的过程,评价逻辑推理素养;

(3)关注学生运用定义法或坐标法求轨迹,评价数学运算素养.

关键能力:(1)关注学生表述立体几何轨迹问题的过程,评价推理论证能力;

(2)关注学生运用定义法或坐标法求轨迹,评价运算求解能力.

2 复习回顾,创设问题

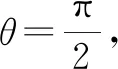
图1

问题1求平面轨迹问题,大家一般用什么方法处理?

生:定义法,直接法(在平面直角坐标系下找到点的横纵坐标之间的关系式),设元消参法.

问题2能否类比平面轨迹问题来处理立体几何中的轨迹问题?

评价：通过复习回顾,关注学生对常见曲线的轨迹定义掌握情况.若学生能在课堂上比较流畅地回答截口曲线轨迹,则可进入下一问题;若学生比较陌生,教师可通过作图展示或严谨推证引导学生认识截口曲线轨迹.评价学生对曲线轨迹的认知水平,发展学生直观想象及数学抽象核心素养.

3 例题探析

例1已知正方体ABCD-A1B1C1D1的棱长为4,M为DD1的中点,N为平面ABCD内一动点.请思考下列问题1～5.

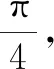
生:直线与平面所成的角即为直线与它在这个平面内的射影所成的角,MN在平面ABCD内的射影为DN,则|DN|=2.根据圆的定义,可知点N的轨迹是以D为圆心,半径为2的圆.

追问1:若求线段MN中点P的轨迹呢?

生:在△DMN中,取DM中点Q,则|PQ|=1,且PQ⊥DD1,则点P的轨迹以Q为圆心,半径为1的圆.

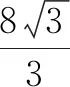
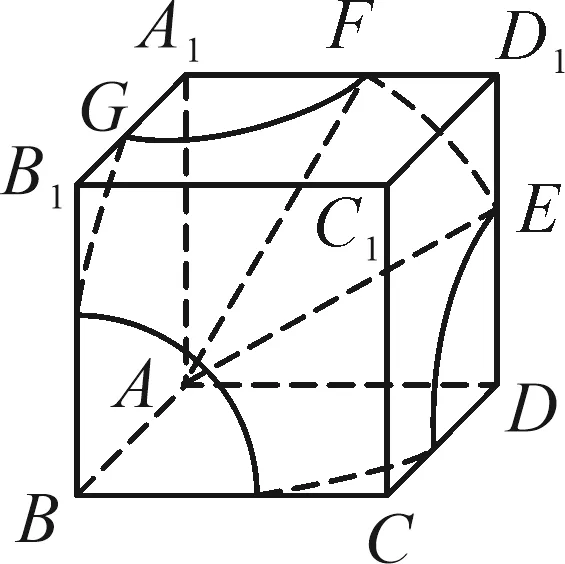
图2

评价：问题1关注学生能否将线面所成角转化为线线所成角,从而将空间问题转化为平面问题进行处理.追问1关注学生能否将空间点P的轨迹问题转化为绕DD1旋转的圆柱被一个垂直于轴的平面截得的圆.追问2通过球面与正方体表面相交引导学生想象曲面与平面相交的问题,关注学生能否将交线问题转化为平面截球面所得截口曲线问题.截口曲线并不是完整的圆,需要通过角度判断曲线的长度;若学生能较好地回答,则可以顺利通过,若学生比较难理解,可以将球被平面截得的截口曲线作出.培养转化与化归、数形结合的数学思想,发展学生的空间想象、逻辑推理核心素养,提高运算求解能力.

问题2若△AC1N的面积为定值,则点N的轨迹是什么?

生:若S△AC1N为定值,又线段AC1长度已知,则点N到直线AC1的距离为定值,即点N在以AC1为轴,定长为半径的圆柱(圆柱没有高度)上.又因为点N在平面ABCD内,所以用一个与旋转轴AC1不垂直的平面截圆柱,截口曲线为椭圆,即点N的轨迹.

问题3若点N到直线BB1与直线DC的距离相等,则点N的轨迹是什么?

生:由题意知点N到点B与直线DC的距离相等,根据抛物线的定义知点N的轨迹是抛物线.

追问3:若平面A1BCD1内一动点P到直线AB1和BC的距离相等,则点P的轨迹是什么?

生:设AB1∩A1B=O,则PO表示点P到直线AB1的距离.因为平面A1BCD1内一动点P到直线AB1和BC的距离相等,所以PO与点P到直线BC的距离相等.根据抛物线的定义,可得点P的轨迹为抛物线．

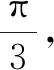
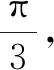
追问4:若点P在平面CDD1C1内,满足∠A1BD1=∠PBD1,则动点P的轨迹是什么?

生:点P在以B为顶点,BD1为对称轴,A1B为母线的圆锥与平面CDD1C1的交线上,又A1B∥平面CDD1C1,所以与圆锥母线平行的平面截圆锥得到的截口曲线是抛物线,即点P的轨迹．

评价：关注学生对圆锥曲线定义的掌握情况,评价学生对轨迹的认知,发展学生数学建模、空间想象、逻辑推理核心素养.

问题5对于问题4,还可以用什么方法来处理?

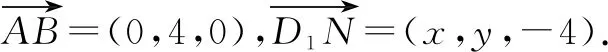
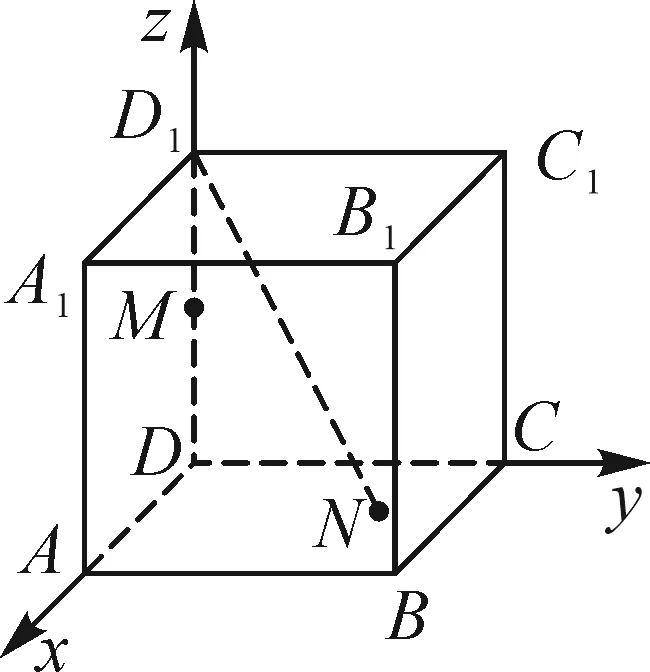
图3

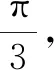
所以点N的轨迹为双曲线．

评价：关注学生用几何法处理问题不容易时,能否想到可通过坐标法实现,对比各自的优缺点,评价转化与化归的数学思想;关注学生能否运用定义法或坐标法求轨迹问题,评价学生对立体几何轨迹问题的运用水平;关注学生能否借助图形寻找几何元素与数量之间的关系及将空间问题转化为平面问题,评价数形结合思想及转化与化归思想的理解水平;关注学生通过不同方法表述轨迹的过程,发展学生数学抽象、直观想象、逻辑推理素养,培养学生推理论证及运算能力.

例2如图4,设点M是长方体ABCD-A1B1C1D1的棱AD的中点,AD=AA1=4,AB=5,点P在面BCC1B1上,若平面D1PM分别与平面ABCD和平面BCC1B1所成的锐二面角相等,则点P的轨迹为( ).

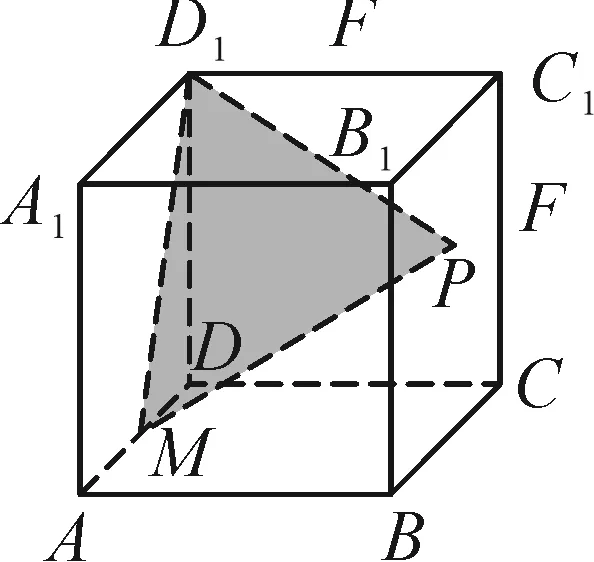
图4

A．椭圆的一部分 B．抛物线的一部分

C．一条线段 D．一段圆弧

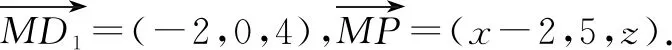
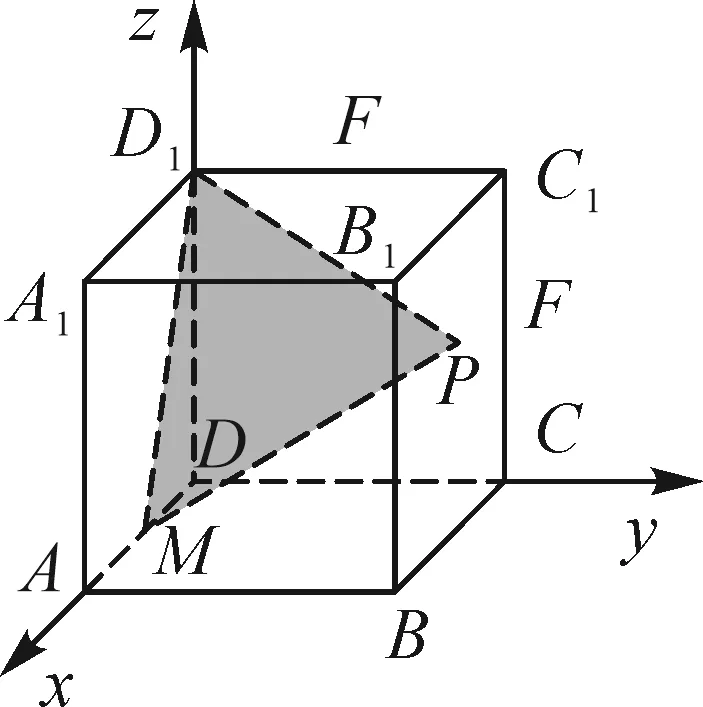
图5

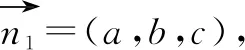
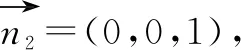
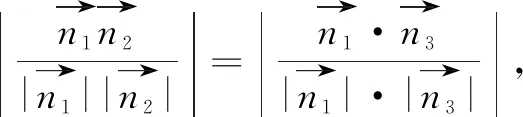
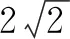
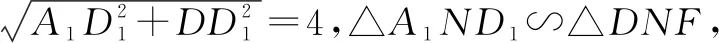
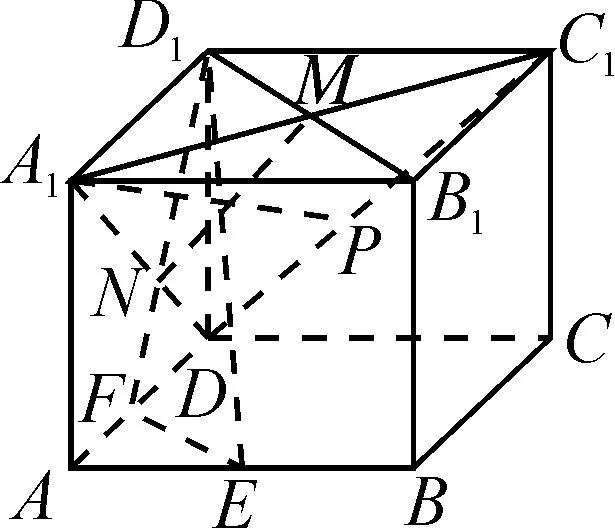
图6

评价：例2、例3关注学生求解轨迹问题的方法选择,坐标法中坐标的正确书写,几何法中量的正确表达以及运算求解能力.通过方程的形式判断轨迹及表述轨迹的过程,关注学生能否将线面交点问题转化为线线交点问题,例3中交点Q的轨迹是平面与平面的交线,寻找这条线的关键是找出两个交点.评价数形结合及转化与化归数学思想的理解水平;发展学生直观想象、逻辑推理核心素养,培养推理论证、运算求解能力.

4 课堂练习

(1)在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且保持AP⊥BD1,则动点P的轨迹为( ).

A．线段B1CB．线段BC1

C．BB1的中点与CC1的中点连成的线段

D．BC的中点与B1C1的中点连成的线段

(2)已知异面直线a,b成60°角,其公垂线段为EF,|EF|=2,长为4的线段AB的两端点分别在直线a,b上运动,则AB中点的轨迹为( ).

A．椭圆 B．双曲线

C．圆 D．以上都不是

评价：通过课堂巩固练习,加深对立体几何轨迹问题的认知,反馈学生对本节课内容的掌握情况,进一步发展学生的能力.

5 课堂小结与课后练习

本文从略,可扫码观看具体内容.

根据学生的认知规律,合理地设计教学过程,再进行学习评价,这样不仅可以提高学生的学习兴趣,提高他们的自我认知,更好地落实数学核心素养,也有利于教师进行教学反思,改进教学,提高教学质量.