抓住轨迹意识,优化解题应用

江苏省常熟市海虞高级中学 刘 莹

轨迹意识是平面解析几何中的一种重要行为意识,也是平面解析几何中的重要思想方法.除在解析几何中熟练应用外,在解三角形、平面向量以及立体几何等其他场合,也经常借助轨迹意识来解决相应的数学问题,直观形象.

1 解析几何中的轨迹意识

解析几何中的轨迹问题,其实质就是由曲线上的动点变化规律,按照一个条件的变化引起其他相关新动点的变化情况,利用对图形结构的理解、探索与联想,构建“形”与“数”之间的联系,进而探究新动点的轨迹.

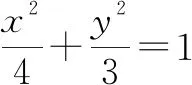
分析：根据条件设出重心的坐标,通过相关点法构建重心的轨迹方程,同时引入直线的斜率参数构建对应的直线方程;通过联立方程组,转化为相应的方程有根的情况,利用判别式法来构建不等式,确定斜率的最值问题.

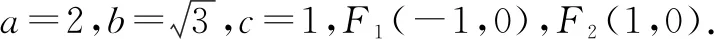
代入椭圆方程,可得点G的轨迹方程为

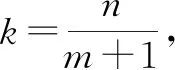
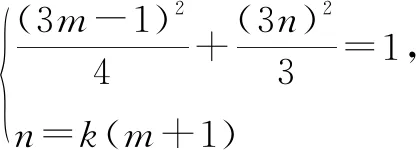
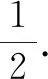
2 解三角形中的轨迹意识

解三角形中的轨迹问题,其实质就是将三角形问题转化为对应的代数问题,合理构建数学模型,利用代数问题所对应的轨迹,反过来数形结合,直观应用,往往可以出奇制胜,简捷有效.

例2(创新题)在△ABC中,内角A,B,C所对的边分别为a,b,c,记△ABC的面积为S.

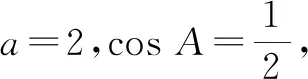
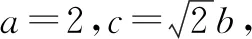
分析：(1)以条件中对应边与角的关系确定三角形的外接圆半径,根据动点A的轨迹,结合平面几何图形的直观来确定△ABC的面积最大时动点A的位置,进而求解相应的面积.

(2)结合三角形中一边为定值,另两边涉及倍数关系,根据平面直角坐标系的构建,将解三角形问题转化为平面解析几何中的动点轨迹问题,数形结合确定动点A的位置,进而求解面积的最大值.

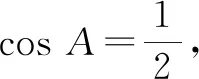
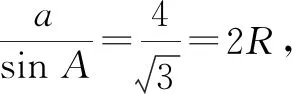
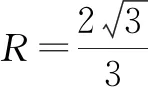
图1

数形结合,易知当顶点A位于优弧BC的中点D处时,△ABC的面积S最大.

此时,△ABC是正三角形,所以

(2)如图2所示,以BC边所在的直线为x轴,以BC边的中垂线为y轴,建立平面直角坐标系xOy,则B(-1,0),C(1,0).

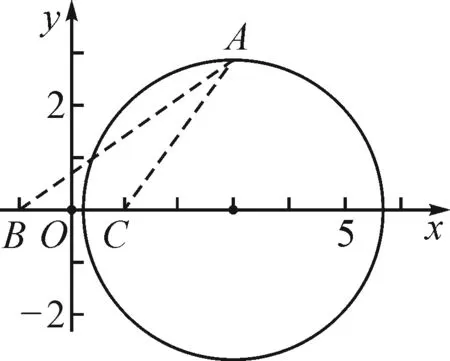
图2

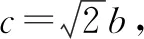
(x+1)2+y2=2[(x-1)2+y2].

整理并化简,可得(x-3)2+y2=8(y≠0),此即为顶点A的轨迹方程.

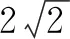
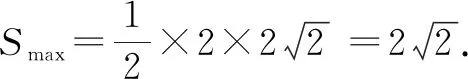
点评：借助解三角形中对应三角形的边或角的某种定量关系,从平面几何视角或平面解析几何视角来确定动点的轨迹,合理构建平面几何或平面解析几何模型,借助“形”的直观去分析与处理一些相关的最值或综合应用问题,更加直观形象,简捷有效.

3 平面向量中的轨迹意识

平面向量中的轨迹问题,其实质就是抽象出平面向量中相关关系式的几何意义,或将线性运算转化为坐标运算等,有效确定动点的轨迹,进而利用动点的变化规律与运动轨迹,依题解答.

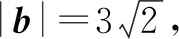
分析：根据题意,构建平面几何图形加以数形结合,利用条件中t∈R确定点A1的轨迹,结合不等式恒成立的条件确定AB⊥OA;通过勾股定理的转化,结合关系式的特征进行三角换元处理,将所求平面向量模的和式转化为三角函数的最值问题.

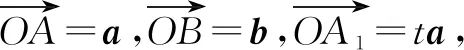
图3

根据题意,对任意t∈R,恒有|b-ta|≥|b-a|,可得|A1B|≥|AB|.

由t∈R,可知点A1的轨迹是直线OA,数形结合可知AB⊥OA.

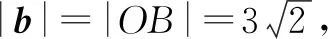
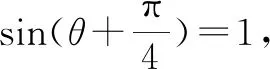
所以|a-b|+|a|的最大值是6.故填答案:6.

点评：借助平面几何图形的直观分析,综合平面向量的几何意义与相关运算,直观形象来确定对应动点的轨迹以及相应的变化规律,数形结合,从而破解起来更加直观,处理起来更加快捷.

4 立体几何中的轨迹问题

立体几何中的轨迹问题,其实质就是合理进行“降维”处理,将将立体几何问题转化为平面几何问题,结合动点的轨迹,综合利用平面几何或解析几何等相关知识来分析与求解.

例4(2022年高考数学北京卷·9)已知正三棱锥P-ABC的六条棱长均为6,S是△ABC及其内部的点构成的集合.设集合T={Q∈S|PQ≤5},则T表示的区域的面积为( ).

分析：根据题设条件,结合立体几何性质,合理构建点P在底面△ABC内的射影点O;结合集合的创新设置进行合理转化,将空间中的距离问题转化为平面内的距离问题,进而利用圆的定义与正三棱锥的性质来确定动点Q的轨迹,进而得以分析与求解.

解析：设点P在底面三角形ABC内的射影为点O.由PA=PB=PC,可知O为△ABC的外心.

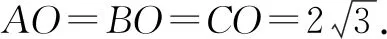
由PA=PB=PC=6,得

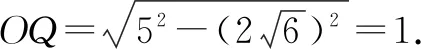
所以,动点Q的轨迹是△ABC内以O为圆心,1为半径的圆及其内部,则其对应的面积为π.

故选择答案:B.

以上通过四类典型问题与实例,从不同视角加以剖析,合理引导学生在解题过程中抓住轨迹意识,对图形变化要有动态认识,学会作图、构图、识图;结合对图形结构的理解,创新构建起良好的“数”与“形”之间的联系,并借助问题破解中的轨迹意识,循序渐进地领悟数形结合核心素养.